基于深度學習的跨分辨率結構拓撲優化設計方法

(北京工業大學 材料與制造學部，北京 100124)

1 引 言

拓撲優化是指在給定邊界條件下，確定設計域內材料的最優分布，從而在滿足約束的情況下使結構性能達到最佳的一種設計方法。相比尺寸和形狀優化，拓撲優化設計具備更多的設計自由度，在工業領域應用潛力更大，公認其為結構優化設計中的熱點與難點問題。傳統拓撲優化設計方法主要包含均勻化方法(Homogenization Method)[1,2]、變厚度法[3]、變密度法SIMP(Solid Isotropic Material with Penalization)[4,5]、漸進結構優化法ESO(Evolutionary Structural Optimization method)[6,7]、水平集法(Level Set method)[8]、移動組件法MMC(Moving Morphable Component)[9]和獨立連續映射法ICM(Independent Continuous Mapping Method)[10,11]等。

傳統拓撲優化方法可以根據約束條件和優化目標等來設計結構優化構型，使結構滿足設計需要。但是，隨著結構單元數量增加，拓撲優化消耗的時間成本顯著增加，這使得精細化拓撲優化設計受到了限制。利用機器學習和深度學習等智能算法減少傳統方法的計算時間，提高拓撲優化效率成為當前結構拓撲優化研究的熱點之一。

相比機器學習算法，深度學習算法擁有更多的網絡層數，通過對數據的反復學習，可以建立輸入和輸出數據之間的高維映射。這種隱式映射關系計算效率高且泛化能力強，將深度學習算法和傳統拓撲優化方法相結合，實現精細、高效和智能的拓撲優化受到國內外學者的廣泛關注。利用深度學習加速拓撲優化設計可以分為同分辨率和跨分辨率拓撲優化設計。

同分辨率拓撲優化設計是指在訓練深度學習模型中，輸入數據和輸出數據保持相同維度，即利用深度學習算法代替迭代計算過程，實現對拓撲優化的加速設計。Sosnovik等[12]利用中間構型作為輸入，使用U-net網絡模型建立中間構型和優化構型的映射關系，實現對SIMP方法的加速設計。Lin等[13]利用相似方法解決了傳熱結構拓撲優化設計問題。Nikos等[14]將深度置信網絡(deep belief network)嵌入SIMP方法中，網絡計算的結果再導入SIMP方法，進行最終優化，提高了計算的精度。同分辨率拓撲優化方法在一定程度上提高了優化計算效率，但是未能實現結構的精細化設計。

為了進一步精細化拓撲構型，提出跨分辨率拓撲優化設計。跨分辨率拓撲優化設計是利用低分辨率邊界條件作為輸入，借助深度學習模型，實現高分辨率結構的設計。Yu等[15]利用卷積自編碼網絡和生成對抗式神經網絡的組合，完成跨分辨率設計。其中，卷積自編碼網絡實現同分辨率拓撲構型預測，生成對抗式網絡完成結構精細化設計。Li等[16]改變網絡組成，利用生成對抗式網絡生成同分辨率的優化構型，進而利用超分辨率生成對抗式網絡完成高分辨率結構設計。跨分辨率拓撲優化設計方法不僅提高了傳統拓撲優化設計效率，而且提高了優化構型設計精度。但是多網絡耦合的方法提高了數據集制作和網絡搭建的復雜度，并且網絡預測結構的誤差會疊加。

為了克服多網絡帶來的設計問題，本文基于CGAN(Conditional Generative and Adversarial Network)設計單一網絡結構實現跨精度結構拓撲優化設計。利用ICM方法建立數據集，訓練網絡模型。該方法避免組合網絡訓練的復雜性，且保證了生成結構的精確度。研究結果產生了一種新的網絡結構應用于結構拓撲優化的加速設計，使精細化拓撲優化設計更加高效和智能。

2 基于ICM方法的結構拓撲優化設計

2.1 拓撲優化模型的建立及求解

ICM方法提出了獨立連續拓撲變量的概念和獨立連續映射方法，將拓撲變量從材料和面積厚度等尺寸優化或形狀優化的變量中抽取出來，用獨立于單元具體物理參數的變量來表征單元的有和無，利于拓撲優化模型的建立。同時引入過濾函數，進行參數識別和設計變量的離散。ICM方法適合任何目標函數，但通常以結構的輕量化作為目標函數，將力學響應量或特征參數等作為約束條件，利用對偶序列二次規劃方法進行優化模型求解，減少了約束數目，降低了求解規模。基于上述理論，其數學模型可以表示為

(1)

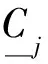
在拓撲優化模型中,目標函數和約束條件均為包含拓撲變量的隱式函數，求解計算比較復雜。將優化模型(1)的約束條件和目標函數進行一階和二階泰勒展開，其表達式為

(2)

(j=0,…,J) (3)

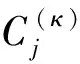
將式(2,3)代入式(1)，優化模型轉化為

(4)

由于優化結果不受常數項的影響，所以在求解過程中省略目標函數的常數項。模型中，拓撲優化方程的系數分別為

(5)

為了減少計算規模并提高模型計算效率，引入對偶理論將二次規劃模型轉化為對偶模型，針對建立的二次規劃模型(4)，其對偶模型可以表示為

(6)

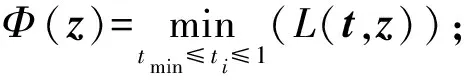
(7)

對于拓撲優化模型(4)，其設計變量和目標函數需要滿足的約束條件為

‖x(κ + 1)-x(κ )‖/‖x(κ )‖≤ε1

(8)

ΔO=|(O(κ + 1)-Oκ)/Oκ|≤ε2

(9)

式中ε1和ε2為設計變量和目標函數需要滿足的收斂精度。迭代完成后，將連續的拓撲變量進行離散化，實現從連續模型到離散模型的轉化。

2.2 位移約束的顯式化

為說明ICM方法與深度學習理論的結合，本文建立了以結構質量最小為優化目標，以結構允許位移為約束的拓撲優化設計模型。

(10)

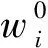
(11)

由莫爾定理，在指定方向上結構在任意單元節點的廣義位移為

(12)

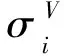
(13)

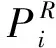
根據整體剛度矩陣方程，式(13)可以轉化為

(14)

式中ki為i單元的剛度矩陣。針對各向同性材料，設計變量和位移約束關系的顯式化為

(15)

式中cj i為位移約束方程系數，其表達式為

(16)

將式(16)代入式(10)，得到位移約束下的數學模型為

(17)

利用2.1節的理論對拓撲優化模型(17)進行模型求解，實現位移約束下結構的拓撲優化設計。

2.3 基于ICM方法的優化算例

利用上述理論，以短懸臂梁為基結構，寬高均為1 m。材料的弾性模型為1 GPa，泊松比為0.3。分別對其進行32×32和64×64的單元劃分，對應低分辨率結構優化設計和高分辨率結構優化設計。位移約束值均設置為57.3 mm。利用基于ICM方法的位移約束拓撲優化程序[17]完成結構優化設計。

通過優化計算，分別獲得了不同分辨率下的拓撲構型，列入表1。當單元數M=32時，優化構型的邊緣表現出明顯的鋸齒結構；單元數M=64時，結構進一步細化，鋸齒邊緣明顯減輕，優化構型質量更高。

表1 ICM方法優化構型

理想情況下，單元劃分越精細，優化結構也會更加準確。兩種單元數量下優化計算的時間如圖1所示，當M=32時，迭代計算時間為3.96 s；M=64時，迭代計算消耗的時間為28.73 s。可見，隨著單元數目的進一步擴大，消耗的時間呈指數型增加。

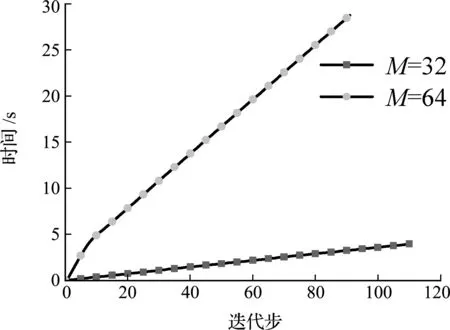
圖1 不同單元數量所消耗的計算時間

ICM方法消耗的時間主要在于每次迭代計算都要進行有限元分析，并且隨著單元數增加，有限元分析消耗的時間也隨之增加，導致計算效率低下。為了減少ICM方法在迭代過程中消耗的時間，提高ICM方法計算效率，引入CGAN深度學習算法，代替傳統計算過程中部分迭代步數，并實現由低分辨率到高分辨率的跨精度加速設計。

3 深度學習模型建立

3.1 CGAN網絡結構

為了實現跨精度拓撲優化加速設計，將CGAN網絡引入到拓撲優化設計過程。CGAN網絡模型屬于無監督學習，在結構上由生成器和判別器組成。生成器利用輸入的低分辨率中間構型為條件預測高分辨率構型；判別器通過判斷生成器預測的構型和優化構型是否一致，實現對生成器的動態訓練。當判別器無法區分預測構型和優化構型時，生成器模型訓練完成，實現跨分辨率優化設計。

3.2 生成器模型

生成器網絡模型主要由卷積層和反卷積層組成，卷積層主要通過卷積核提取低分辨率中間構型的重要特征，實現維度降低。反卷積層是利用卷積層提取特征數據，利用反卷積計算進行特征重組和結構重建，以達到結構預測目的。為了實現跨分辨率結構預測，反卷積層輸出維度為卷積層輸入維度的4倍。

如圖2所示，生成器輸入為32×32像素圖片，這與低分辨率構型維度一致。隨著卷積網絡層數增加，特征層維數依次為32-32-16-8-4-2-1。隨著特征層維數的減小，特征層層數不斷增加，依次為64-64-128-256-512-512-512。這些低維特征層，將作為優化構型重構重要特征。與卷積層結構相反，反卷積層特征維數不斷增加，其變化規律為1-2-4-8-16-32-32；特征層層數為1024-1024-1024-1024-512-256-128。反卷積層和卷積層之間存在跳躍連接，所以反卷積層中，特征層數是對應卷積層數的兩倍。跳躍連接使卷積層中的信息直接傳遞給反卷積層。這種傳遞使得反卷積層獲得更多的特征信息，在一定程度上提高了預測構型的精度。在反卷積計算之后，還跟隨著三個卷積層，用于提高預測結構維度。

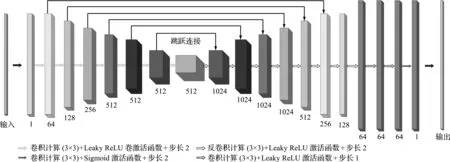
圖2 生成器網絡結構

3.3 判別器模型

判別器主要由卷積層組成，基于one-hot編碼，對生成器生成的結構進行評估。如圖3所示，判別器由六個卷積層構成，這些卷積層用來提取優化構型和預測構型的特征，并輸出對應的概率，而后反向訓練網絡結構。前五層卷積計算中都緊跟著正則化層和激活函數層(Leaky ReLU),Leaky ReLU激活函數使得負半軸信息不會完全丟失，提高了網絡魯棒性。 最后的一個卷積層后不再使用正則化層，并且使用Sigmoid函數作為激活函數。

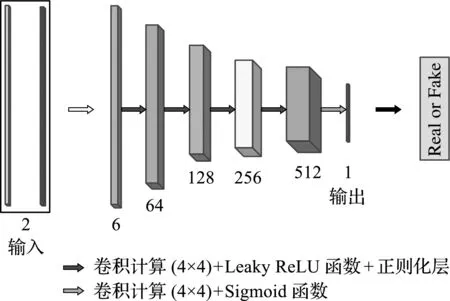
圖3 判別器網絡結構

3.4 模型的訓練與評估

在CGAN模型訓練過程中，主要包含生成器損失和監視器損失，這些損失用于計算生成器和判別器的誤差，利用反向傳播算法優化權重。

生成器損失是用來提高監視器對預測構型的評估概率，其由交叉熵損失(BCE loss)和平均絕對損失(MAE)兩部分組成。 交叉熵損失函數可以表示為

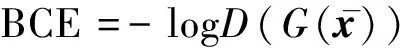
(18)

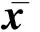
絕對損失函數是用來衡量預測構型和優化構型的差異，其公式為

(19)

式中y為優化構型。所以，生成器的整體損失為

(20)

式中λ為常系數，一般取值為100。

判別器損失是一個標準的二分類交叉熵損失函數，其公式為

(21)

模型完成訓練后，將預訓練模型用來預測高分辨率優化構型。引入感知哈希算法(Perceptual hashing algorithm)，用于評估預測構型和優化構型的相似度。首先，將預測構型和優化構型中所有像素的灰度值進行均值計算，獲得灰度均值(Havg)， 其公式為

(22)

式中Pi j為灰度圖的像素值。然后，將圖中所有的像素值與均值作比較，如果大于均值，哈希值為1，相反，哈希值為0，其公式為

(23)

式中Hi j為哈希值。兩個結構的相似度計算結果可表示為

(24)

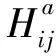
4 數值算例

跨分辨率拓撲優化加速設計方法是利用ICM方法和CGAN網絡組合形成的耦合算法。首先，利用ICM方法建立拓撲優化數據集，數據集包含初始低分辨率中間構型和高分辨率優化構型；其次，搭建基于CGAN的深度學習模型，在數據樣本訓練下，獲得預訓練的網絡模型；最后，將低分辨率中間構型輸入預訓練網絡結構，網絡直接生成優化結構，完成優化設計。圖4展示了利用CGAN模型進行跨分辨率加速設計的流程。

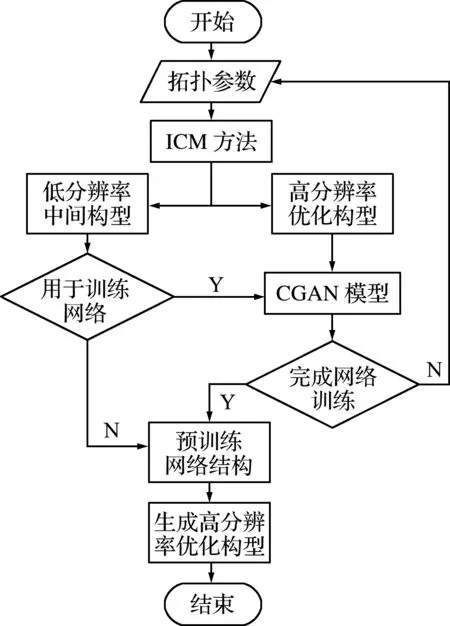
圖4 耦合算法流程

通過利用基于ICM方法的位移約束輕量化拓撲優化計算程序，得到1000個低分辨率的中間構型和對應的高分辨率優化構型，二者組成含有1000個樣本的數據集。數據集劃分為訓練集和測試集，其比率為7:3。對CGAN模型超參數進行設定,生成器和判別器模型的學習率均為0.0001，小批量數據設置為2，總世代循環次數Epoch=200，訓練模型所使用的優化器均為ADAM優化器。

經過數據集準備和模型配置，網絡模型完成訓練過程。圖5展示了網絡的損失變化趨勢和預測構型的精度趨勢。當Epoch≤25時，網絡整體損失快速下降；當Epoch>25時，網絡的損失趨于穩定；損失曲線表明網絡結構具有良好的收斂性。訓練過程利用感知哈希算法對網絡預測構型進行評估。當Epoch≤40時，預測結構與優化構型的相似度迅速增加；當Epoch>40時，逐漸趨于穩定。表2展示了不同訓練階段下，對跨分辨率結構的預測結果。從構型結構上分析，當Epoch=0時，網絡為初始化權重，所以生成的結構為隨機噪音；當Epoch<40時，網絡損失快速收斂，預測的構型也趨于目標構型；當Epoch≥40時，預測構型與目標構型已經非常相似。訓練過程中預測構型、相似度和網絡損失曲線的趨勢基本保持一致。

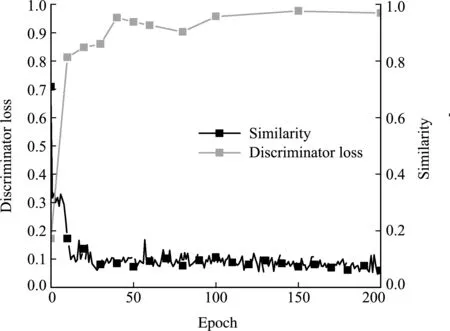
圖5 網絡的損失曲線

針對預訓練的網絡結構，選取50個隨機低分辨率中間構型來測試網絡性能。這些中間構型獨立于訓練集和測試集。將這些迭代計算一次構型輸入到網絡中，網絡計算消耗時間非常微小，平均時間為0.005 s。如表2所示，根據不同中間構型，網絡預測出跨精度優化構型，預測構型和優化構型差異非常微小。

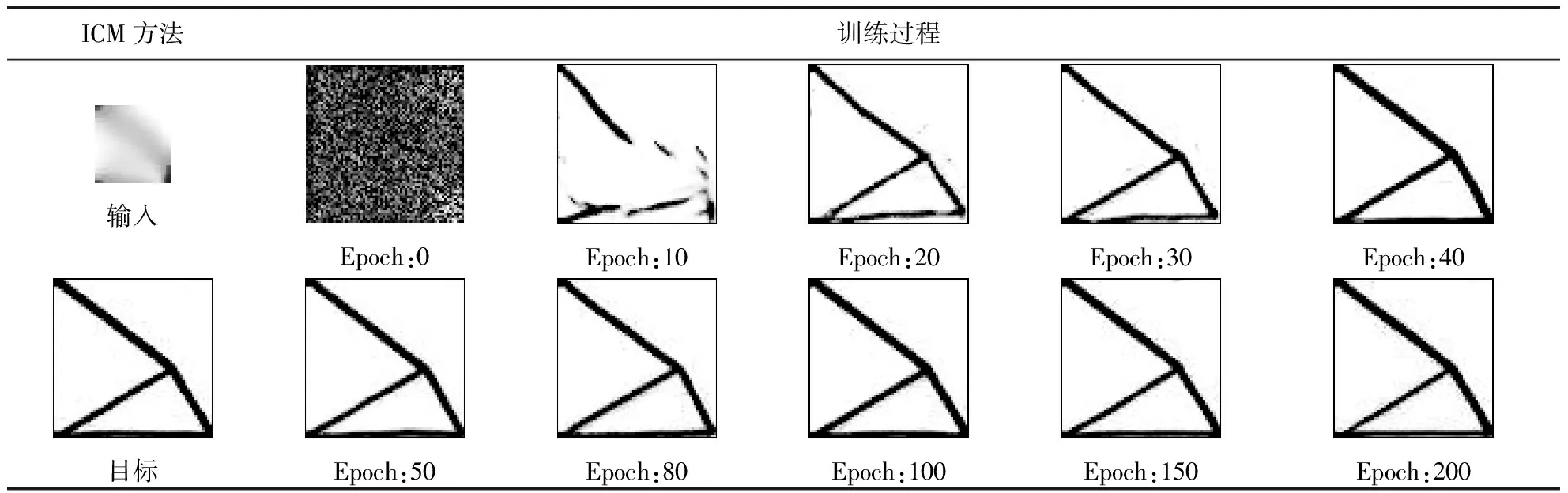
表2 訓練過程中的預測構型Tab.2 Predicted configurations in the training process

網絡加速設計的預測構型相似度和計算時間可以進一步評估。針對表3的預測構型，其結構相似度和計算時間列入表4。可以看出，利用CGAN網絡預測的優化構型，其平均精度為 95.20%。在保證構型精度的前提下，利用網絡加速實現高分辨率構型預測消耗的平均時間為0.071 s，其中包含了ICM方法迭代計算一次的時間和深度學習網絡計算的時間。在計算效率上，跨分辨率方法使用時間不足ICM方法的1%。仿真結果表明，利用CGAN網絡可以高效準確地完成高精度優化構型的計算，提高了ICM方法的計算效率。

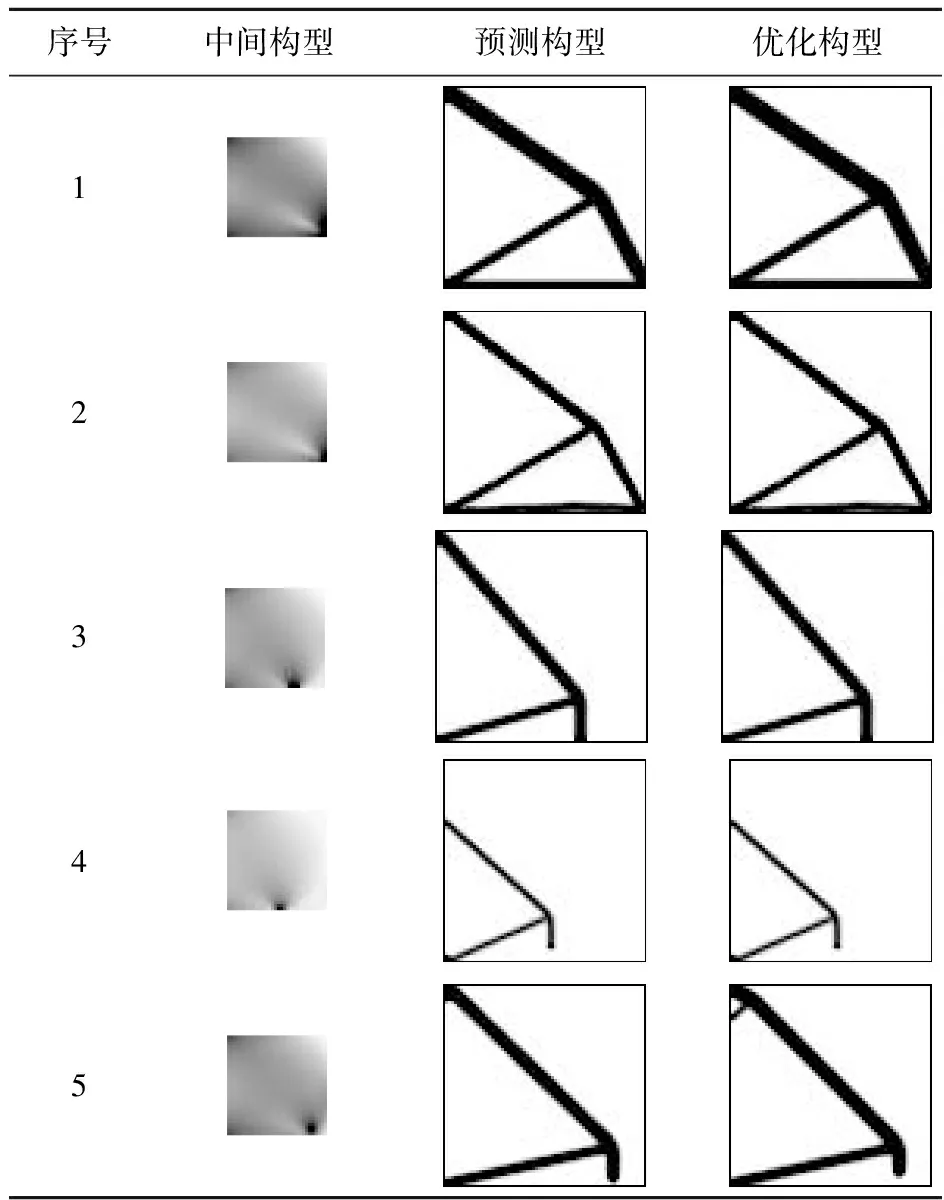
表3 利用網絡預測優化構型

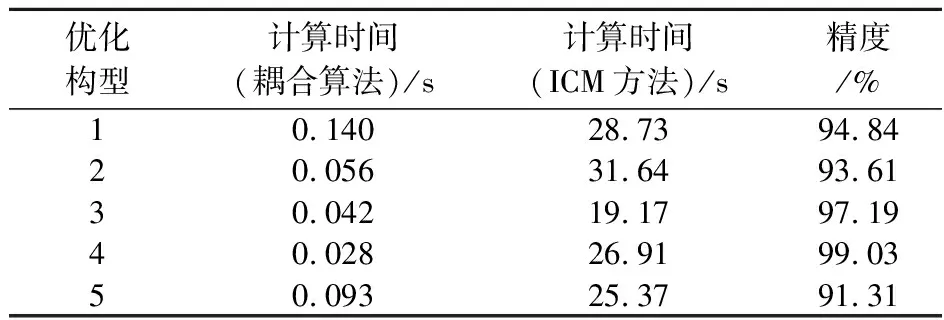
表4 計算時間和精度分析

5 結 論

本文提出了一種基于CGAN網絡的深度學習模型實現跨精度拓撲優化加速設計的方法。利用ICM方法建立的位移約束拓撲優化模型獲得了跨分辨率數據集，利用數據集訓練CGAN網絡，獲得了預訓練網絡結構，實現跨分辨率拓撲構型的預測。數值算例仿真結果表明，在保證結構精度前提下，利用深度學習網絡可以大幅提高拓撲優化計算效率。該研究方法為高精度和高效率拓撲優化設計提供了一種參考。此外，將傳統拓撲優化與深度學習相結合的思路，對于不同約束條件和不同結構類型的拓撲優化問題同樣適用。

參考文獻(References):

[1] Hassani B,Hinton E.A review of homogenization and topology optimization II—Analytical and numerical solution of homogenization equations[J].Computers&Structures,1998,69(6):719-738.

[2] Hassani B,Hinton E.A review of homogenization and topology optimization III—Topology optimization using optimality criteria[J].Computers&Structures,1998,69(6):739-756.

[3] 王 健,程耿東.應力約束下薄板結構的拓撲優化[J].固體力學學報,1997,18(4):37-42.(WANG Jian,CHENG Geng-dong.Optimal topology design of thin plate with stress constraints[J].ActaMechanicaSolidaSinica,1997,18(4):37-42.(in Chinese))

[4] Sigmund O.A 99 line topology optimization code written in Matlab[J].StructuralandMultidisciplinaryOptimization,2001,21(2):120-127.

[5] Andreassen E,Clausen A,Schevenels M,et al.Efficient topology optimization in MATLAB using 88 lines of code[J].StructuralandMultidisciplinaryOptimization,2011,43(1):1-16.

[6] Xia L,Zhang L,Xia Q,et al.Stress-based topolo -gyoptimization using bi-directional evolutionary structural optimization method[J].ComputerMethodsinAppliedMechanicsandEngineering,2018,333:356-370.

[7] Yang H,Ma X W,Jiao F,et al.Preform optimal design of H-shaped forging based on bi-directional evolutionary structural optimization[J].TheInternationalJournalofAdvancedManufacturingTechnology,2019,101(1-4):1-8.

[8] Wang M Y,Wang X M,Guo D M.A level set method for structural topology optimization[J].ComputerMethodsinAppliedMechanicsandEngineering,2003,192(1-2):227-246.

[9] Zhang W S,Chen J S,Zhu X F,et al.Explicit three dimensional topology optimization via Moving Morphable Void (MMV) approach[J].ComputerMe-thodsinAppliedMechanicsandEngineering,2017,322:590-614.

[10] 隋允康,葉紅玲.連續體結構拓撲優化的ICM方法[M].北京:科學出版社,2013.(SUI Yun-kang,YE Hong-ling.ContinuumTopologyOptimizationMethodsICM[M].Beijing:Science Press,2013.(in Chinese))

[11] Ye H L,Wang W W,Chen N,et al.Plate/shell structure topology optimization of orthotropic material for buckling problem based on independent continuous topological variables[J].ActaMechanicaSinica,2017,33(5):899-911.

[12] Sosnovik I,Oseledets I.Neural networks for topology optimization[J].RussianJournalofNumericalAnalysisandMathematicalModelling,2019,34(4):215-223.

[13] Lin Q Y,Hong J,Liu Z,et al.Investigation into the topology optimization for conductive heat transfer based on deep learning approach[J].InternationalCommunicationsinHeatandMassTransfer,2018,97:103-109.

[14] Kallioras N A,Kazakis G,Lagaros N D.Accelerated topology optimization by means of deep learning[J].StructuralandMultidisciplinaryOptimization,2020,62(3):1185-1212.

[15] Yu Y,Hur T,Jung J,et al.Deep learning for determining a near-optimal topological design without any iteration[J].StructuralandMultidisciplinaryOptimization,2019,59(3):787-799.

[16] Li B T,Huang C J,Li X,et al.Non-iterative struc-tural topology optimization using deep learning[J].Computer-AidedDesign,2019,115:172-180.

[17] Yi G L,Sui Y K.An adaptive approach to adjust constraint bounds and its application in structural topology optimization[J].JournalofOptimizationTheory&Applications,2016,169(2):656-670.