結構拓撲優化局部性能約束下輕量化問題的互逆規劃解法

隋允康， 彭細榮*2， 葉紅玲， 李宗翰

(1.北京工業大學 材料與制造學部，北京 100022; 2.湖南城市學院 土木工程學院，益陽 413000)

1 引 言

錢令希[1]指出力學性能約束可劃分為局部性約束和整體性約束，這是就截面層次優化的劃分，同樣也適用結構拓撲優化層次[2-5]。

力學性能局部性與整體性的區別直接影響建模與求解的差別。局部性力學性能約束下的結構優化問題中，出現了建模困難。因約束太多，其個數是單元或子域的個數與載荷工況的乘積。不管應力和局部穩定還是疲勞壽命約束，相關性能在每個單元或子域上都必須滿足。而整體性力學性能約束，如位移或頻率約束，約束數目相比局部性能約束少很多，相應的敏度計算量也因為各種處理如采用伴隨法而變得比局部性能約束少很多。

局部性能與整體性能的本質區別在于單元對于性能的作用不同，局部性約束要求在所有單元里相關的性能都不能違背，故稱為單元滿足型；整體性約束只要求結構總體不能違背相關的性能，故稱為性能的單元貢獻型。為了克服局部性能約束優化問題的困難，以往研究已提出過分部[1,2-5]、化整[3-5]及集成[2,3,9-13]3種解法，分別簡稱為P解法(Partition approach)、G解法(Globalization approach)和I解法(Integration approach)。本文將闡述與之相關新提出的3種交融(Blending)即B解法,分部-集成(Partition-Integration approach)即 P -I 解法、化整-集成(Globalization-Integration approach)即G -I解法以及集成-集成(Integration-Integration approach) 即I -I解法。

2 局部性能約束優化問題四種解法的演化

2.1 P解法

在Schmit[6]奠定結構優化成為獨立學科基礎之前，結構設計的滿應力準則其實就是分部優化解法。Shanley等[7,8]提出的同步失效準則，為解決航空結構受壓構件設計需要確定每個截面一組尺寸集，本質上還是分部優化解法。文獻[1]除了敘述桁架滿應力設計，還敘述了鋼框架和鋼筋混凝土框架的構件優化設計，也歸于分部優化解法。分部優化解法的前提是在超靜定結構中引進內力暫時不變的處理，或者說引入了每輪設計中結構靜定化假設。文獻[2-5]在連續體結構拓撲優化的一系列研究中，也沿用了結構靜定化假設。

2.2 G解法

能否在建模時把各單元的相互關聯和影響考慮進去？該想法導致產生了應力全局化方法，即化整優化方法[3-5]。

2.3 I解法

Yang等[9]最先提出了用K-S函數將眾多應力約束集成為一個，進行結構拓撲優化設計。文獻[10,11]也采用凝聚函數包括K-S函數集成應力約束的結構拓撲優化研究，并作了詳細闡述[2,3]。Paris等[12]及Luo等[13]先后引用K-S函數將結構拓撲優化應力約束集成化。將眾多約束化為一個，是化整優化方法和集成優化方法的共性，但是前者借助于力學原理，后者則借助于數學公式。

2.4 B解法

B解法是新提出的交融優化方法，細分為3種(P -I，G -I和I -I)解法，皆植根于互逆規劃的定理2[14,15]。3種交融優化方法在每一次迭代求解中，都包括單目標方和多目標方兩部分，交替求解局部性約束的優化模型，較之局部性約束的P，G和I解法，3種B解法分別提高了求解效率。

3 疲勞性能的分部特點和化整變換

3.1 疲勞性能約束同應力約束的類比

疲勞約束如同應力約束，都屬于單元性能滿足型約束，相應的結構優化模型表示為

(1)

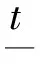
若是靜定結構，其內力不隨設計變量變化而改變，同應力約束問題類似，可求解N個單元疲勞壽命子問題，求解后Li l(ti)不變，一次就求得結果。連續體屬于超靜定結構，不可能像靜定結構那樣結構分析一次就得到最優解，但是可以借助靜定化假設，迭代逼近式(1)的整體最優解。仿滿應力準則，可以稱此為滿疲勞設計準則。

3.2 從單元疲勞壽命化整出結構疲勞壽命

既然應力約束優化可借助應變能化整為全局約束，那么對于疲勞約束，也能做類似的工作。為此，考慮循環載荷下的應力壽命S -N曲線，按巴士昆(Basquin)公式，有

σ=AL- m

(2)

式中σ為疲勞循環下受拉實驗桿的材料極限應力，L為對應的疲勞壽命，A與m為材料給定的相關量，皆為正數。

由式(2)可推得能量的表達式為

(3)

式中e為實驗桿的應變能，v為桿的體積，E為楊氏模量。

把式(3)推廣到單元復雜應力狀態下的疲勞問題，可以得到

(4)

為了推導出疲勞約束全局化的公式，須把式(4)用于結構疲勞問題的單元上，稍加整理，然后求和可以得到結構疲勞壽命的表達式為

(5)

式中ei l與Li l分別為l工況下i單元的單元應變能與單元疲勞壽命，vi為i單元體積。右邊表示l工況下i單元的壽命之和，故可以稱為疲勞載荷l工況下的結構壽命。

3.3 疲勞過濾函數及其在疲勞約束顯式化中的作用

沿襲以往的研究，基于ICM方法，利用不同的過濾函數，將結構拓撲優化模型近似顯式化。為此，類比對應力約束的處理措施[3-5]，給出疲勞約束對應的有關公式。

在應力約束的拓撲優化中，涉及到P解法、G解法和I解法，當中相應的過濾函數有不同的選擇。

P解法的應力約束若取應力為約束[3,4]，有

(6)

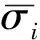
P解法的疲勞約束，類比應力約束式(6)得

(7)

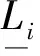
若取應變能表示P解法的應力約束，單元應力約束和全局化的結構應力約束可表示為

(8a)

(8b)

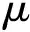
式(8a)左端為結構應變能，其單元應變能為

(9)

式中σi l，εi l與Pi l為l載荷工況下i單元的應力、應變與節點力向量，Ki與Ωi分別為i單元的剛度矩陣及子域。

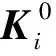
(10)

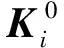
(11)

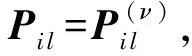
(12)

至此，將式(12)代入式(5)的第i項得

(13)

于是，得到G解法疲勞性能化整之后全局化的結構壽命約束為

(14)

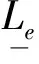
3.4 疲勞約束與應力約束的統一規格

為了疲勞約束優化問題的求解與應力約束優化問題的求解一致，引入了倒壽命的概念，

I=1/L

(15)

在倒壽命概念下，由式(7，13，14)得

(16a)

(16b)

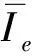
將式(12)代入式(8)得

(17a)

(17b)

式(16,17)表明疲勞與應力統一了約束規格。

順便歸納一下過濾函數的取法,(1) 應力約束時，P解法和I解法皆按式(6,17a)取；G解法按 式(17b)取。(2) 疲勞約束時，P解法和I解法按 式(16a)取；G解法按式 (16b)取。

4 局部性能約束單目標模型三種解法

本節補充和完整了已有的局部性能約束解法，屬于單目標模型分別為分部、化整和集成解法三種，下面分別用P模型、G模型和I模型表示。

4.1 P解法(Partition approach)

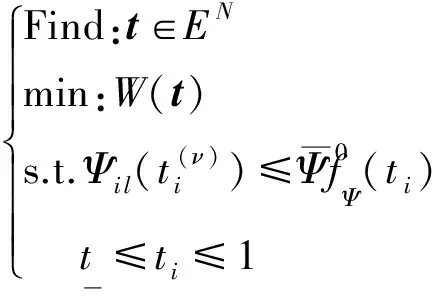
(18)

式中性能符號Ψ為應力或疲勞壽命，當為應力時，按式(6)或式(17a)取；當為疲勞壽命時，按式(16a)取。依靜定化假設求得

(19)

式(19)尚需按變量的上下限予以修正。

4.2 G解法(Globalization approach)

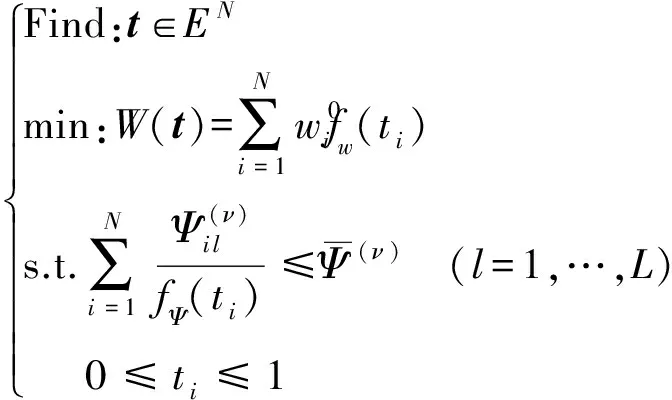
(20)

其中性能符號Ψ分別由式(17b)或式(16b)取得。可采用DSQP或DP -EM方法[16]求解。

4.3 I解法(Integration approach)

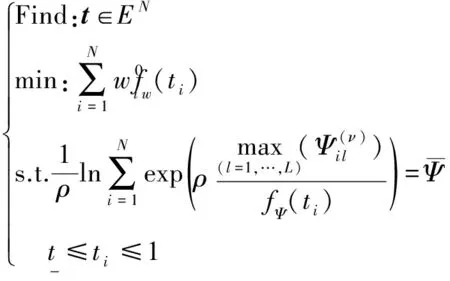
(21)

(22)

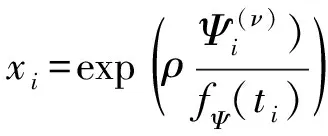
(23)

接著，將式(21)轉化到x空間里，通過目標二階近似，用Lagrange乘子法求得顯式解，迭代逼近，得

(24)

回代到t空間里得式(21)的解。篇幅所限，詳細推導過程從略。

5 局部性能約束的單目標與多目標模型交替迭代的三種交融解法

5.1 三種交融解法

本節突破和開拓出了局部性能約束的新解法，屬于單目標與多目標模型交替迭代的交融解法，共三種：(1) P -I 解法(Partition-Integration approach)； (2) G -I 解法(Globalization-Integration approach)； (3) I -I 解法(Integration-Integration approach)。

標識三種解法的前一個字母，代表第4節的三種單目標模型；后一個字母，代表第5.3節即將介紹的多目標的集成模型，唯有一種。

5.2 交融解法的迭代尋優算法

(1) 迭代次數賦初值ν=1。

(2) 實施模塊1,即進行結構分析。

(3) 實施模塊2,建立4.1～4.3三種模型之一，求解得最優重量W*。

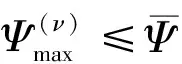
(6) 結束迭代。

5.3 交融解法中的多目標集成模型

多目標模型集成模型可寫為

(25)

式中目標函數的含義與第4.1節P模型的約束相同，此處不再贅述。用Lagrange乘子法推導出規劃(25)的顯式解，

(26)

迭代求解中，當t(v + 1)與t(v )充分接近后收斂，每次小循環迭代都用0≤ti≤1修改迭代解。限于篇幅，具體推導從略。

6 數值算例

6.1 MBB梁的應力約束拓撲優化

基結構是寬為300 mm、高為50 mm簡支梁，集中載荷F=200 N作用于跨中頂點，因對稱性取一半結構和一半載荷進行計算，計算簡圖和支座約束如圖1所示，采用150×50網格。彈性模量E= 2.1×105MPa，泊松比為0.3。為避免應力集中，F分散作用在相鄰的4個結點上，右下角豎向約束也分散在2個結點上。許用應力[σ]=100 MPa。

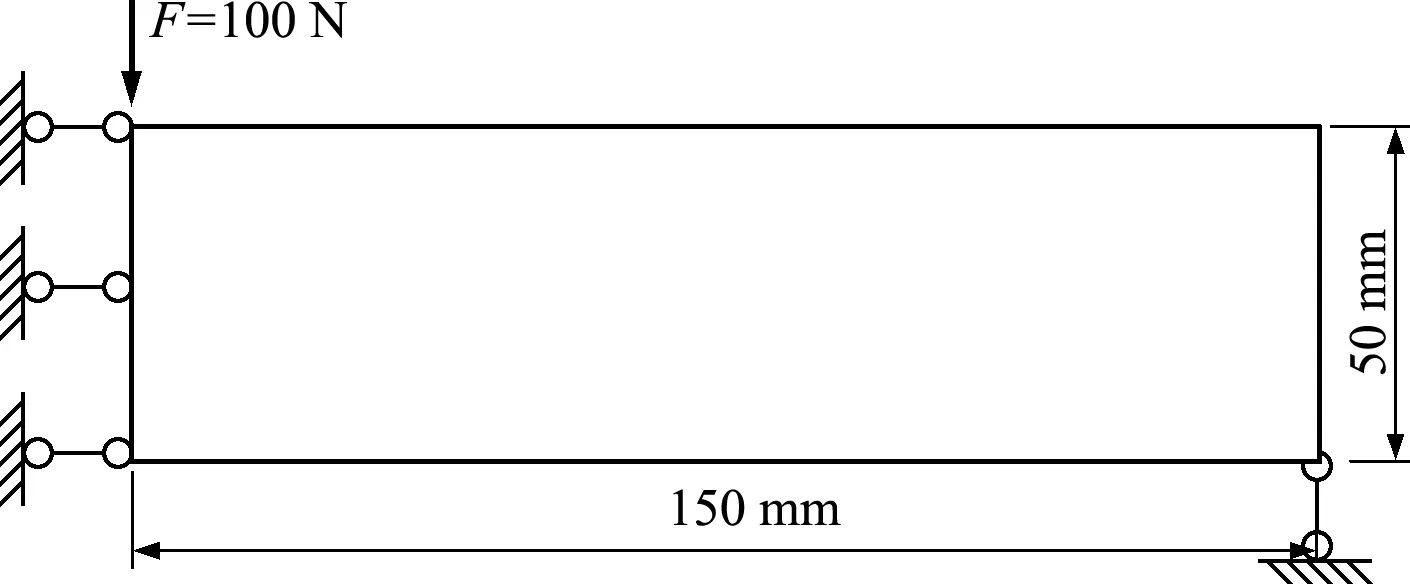
圖1 MBB梁問題取一半結構的分析及優化模型

本算例分別以單純集成方法(I解法)及集成-集成交融方法(I -I 解法)求解應力約束體積極小化問題。I解法經過61次迭代收斂，最優體積比為 0.548，最大Mises應力為100.373 MPa。I -I 解法經過47次迭代收斂，最優體積比為0.553，最大Mises應力為99.900 MPa。兩種方法得到的最優拓撲如圖2所示，對應的Mises應力分布如圖3所示，目標及約束的迭代歷史曲線對比如圖4所示。相比I解法，I -I解法的迭代次數減少了14次，收斂更快。

圖2 單純集成方法與集成-集成交融方法得到的最優拓撲

圖3 單純集成方法與集成-集成交融方法的最優時Mises應力分布

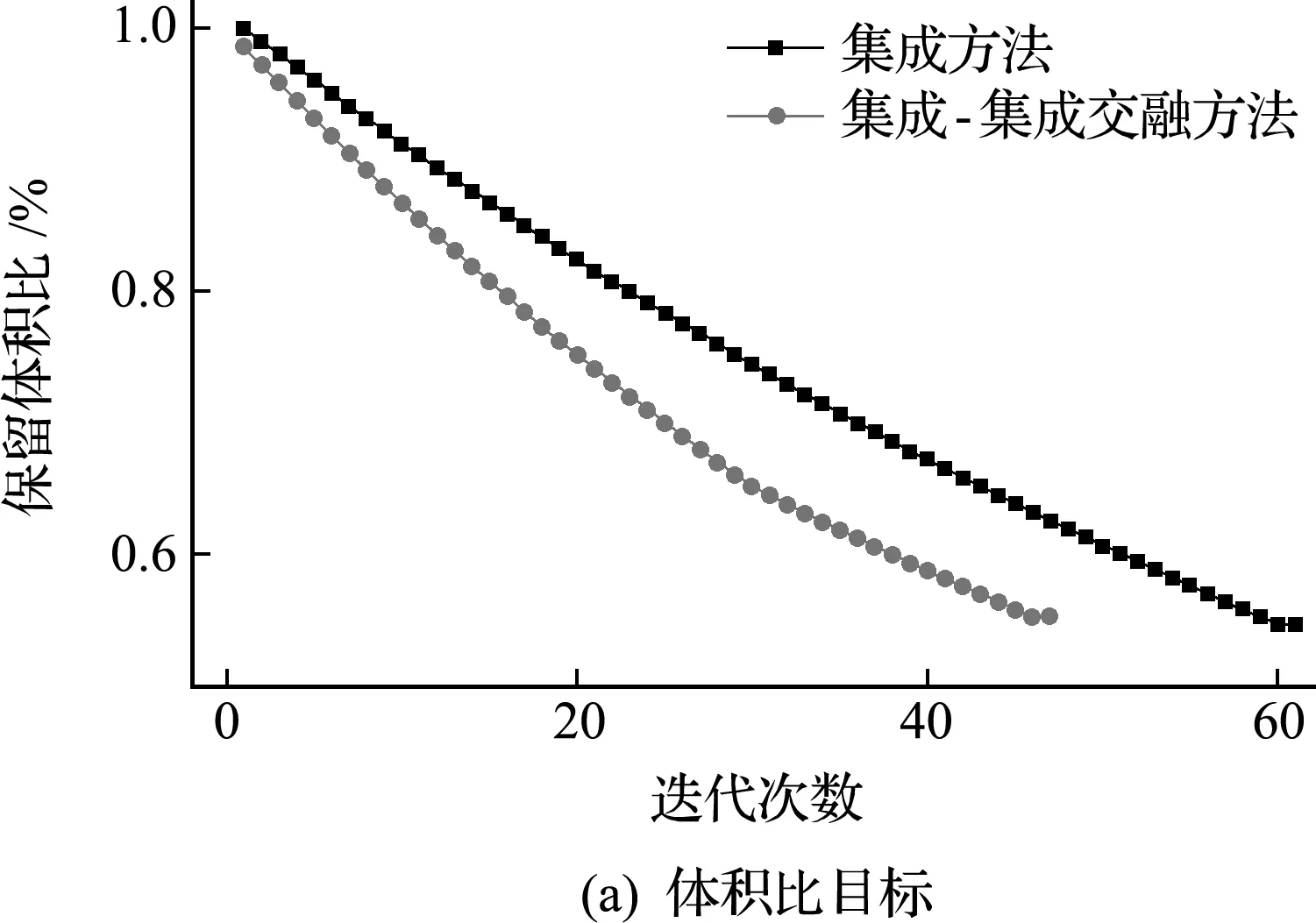
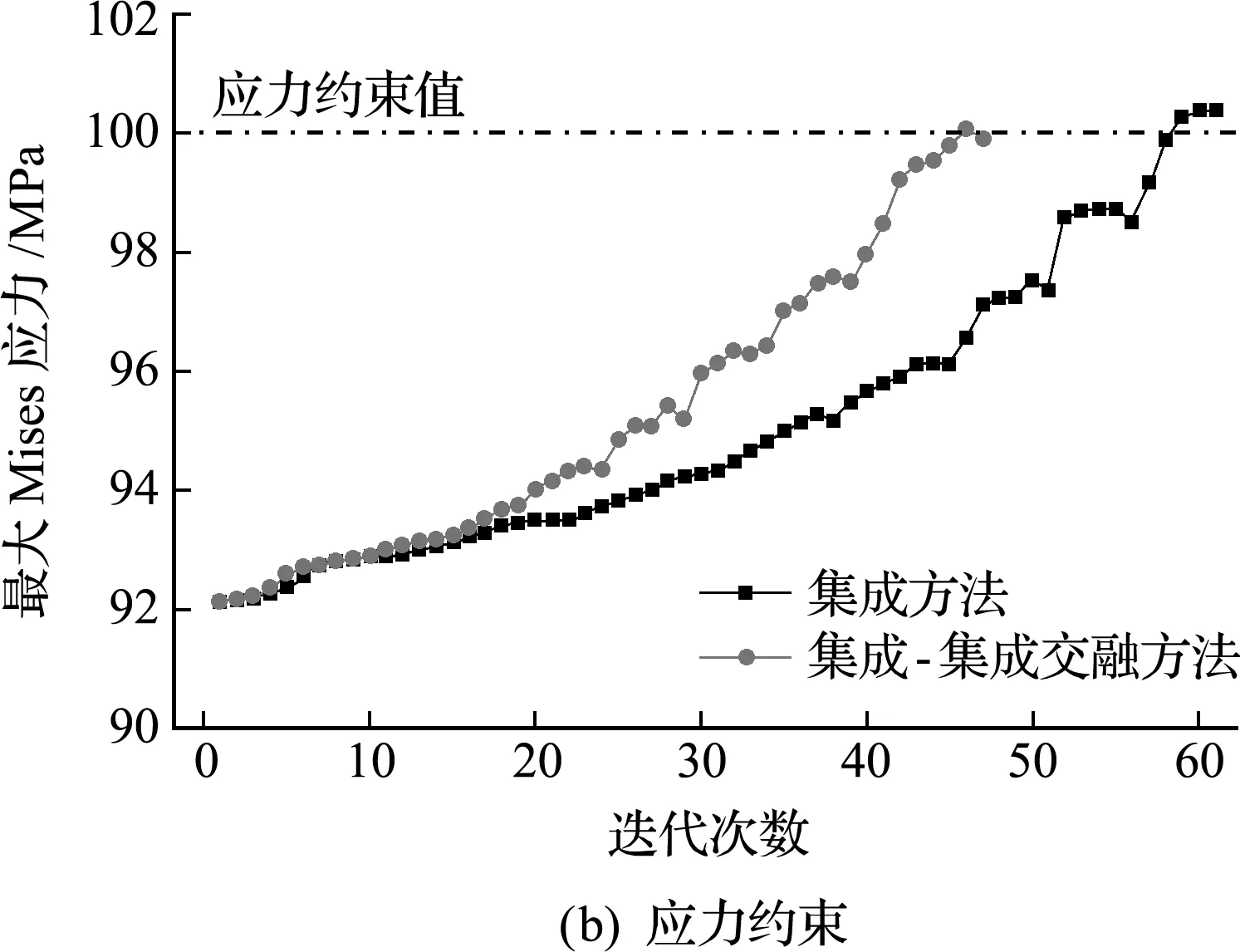
圖4 集成方法與集成-集成交融方法優化過程目標及約束對比

6.2 兩端固支梁的應力約束拓撲優化

如圖5所示，基結構尺寸為120 mm×60 mm×1 mm的平面體，采用200×100網格。材料彈性模量為E=2.1×105MPa，泊松比ν=0.3。左右邊界固定。工況1,集中載荷F1=300 N作用于上邊界中點；工況2, 集中載荷F2=300 N作用于下邊界中點。劃分為200×100個矩形單元。應力約束為100 MPa。

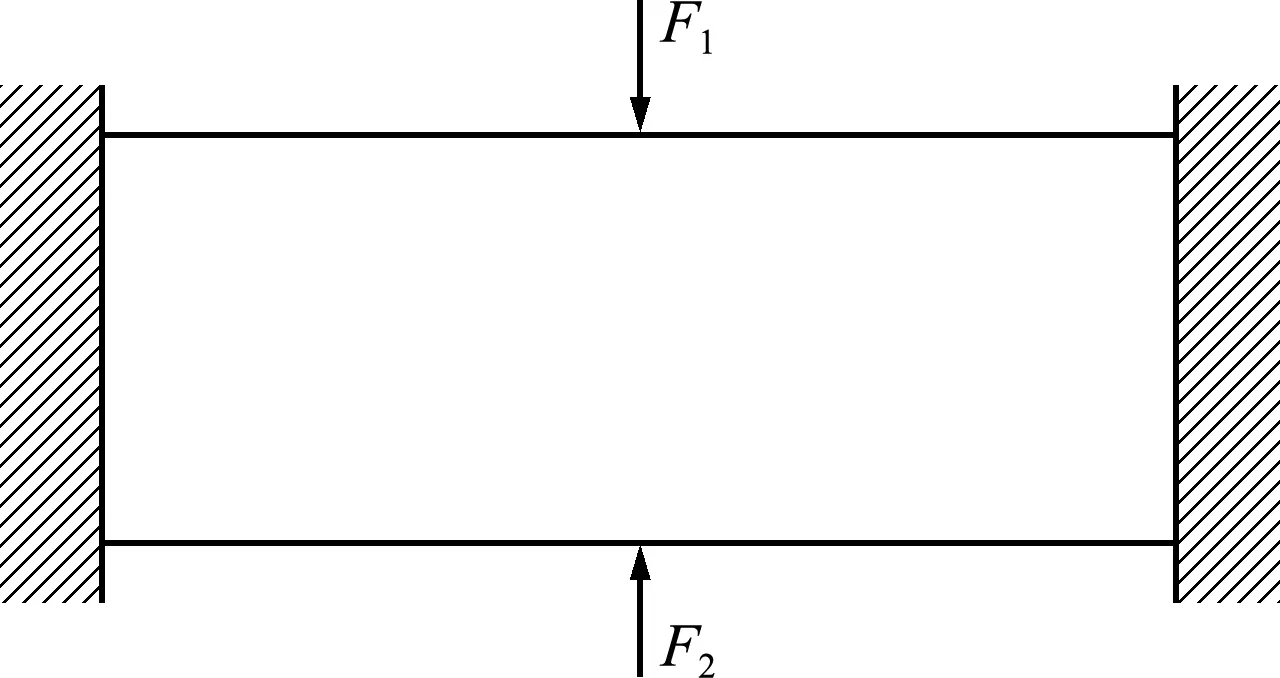
圖5 兩工況算例分析及優化的模型

I解法經過64次迭代收斂，最優體積比為 0.170，最大Mises應力為102.590 MPa。I -I 解法經過57次迭代收斂，最優體積比為0.142，最大Mises應力為96.58 MPa。兩種方法得到的最優拓撲如圖6所示，對應的兩個工況下的Mises應力分布如圖7和圖8所示，目標及約束的迭代歷史曲線對比如圖9所示。經對比可以看出，兩種方法得到的最優拓撲構型不僅相似，對應的Mises應力也是相似的。I -I 解法得到的最優體積比略小。相比I解法，I -I 解法的迭代次數減少了7次，收斂 更快。

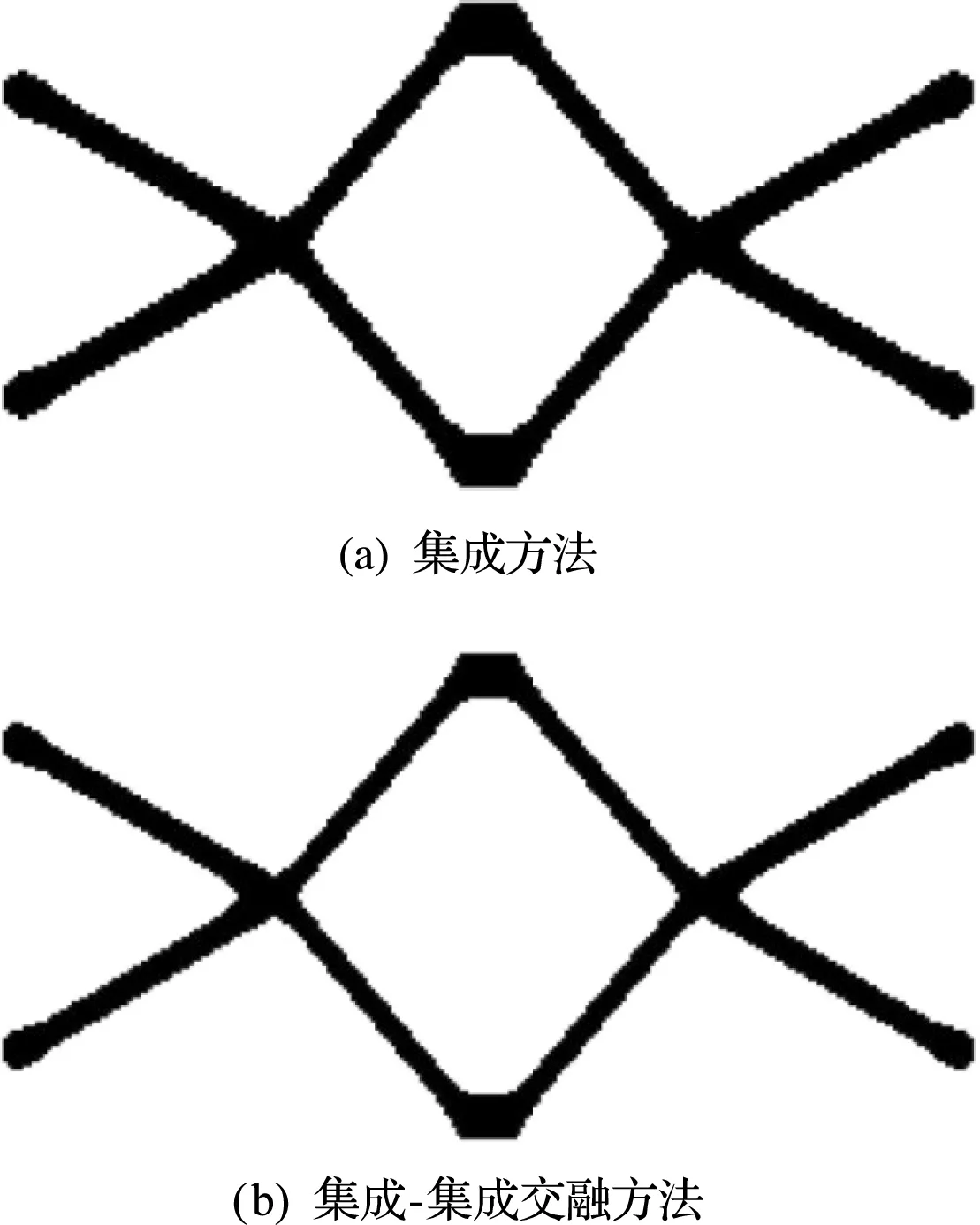
圖6 集成方法與集成-集成交融方法得到的最優拓撲

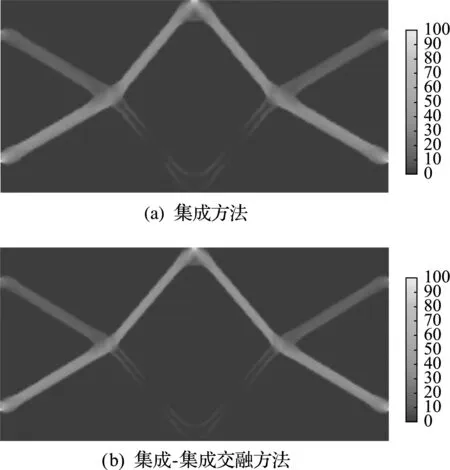
圖7 集成方法與集成-集成交融方法的最優時工況1的Mises應力分布

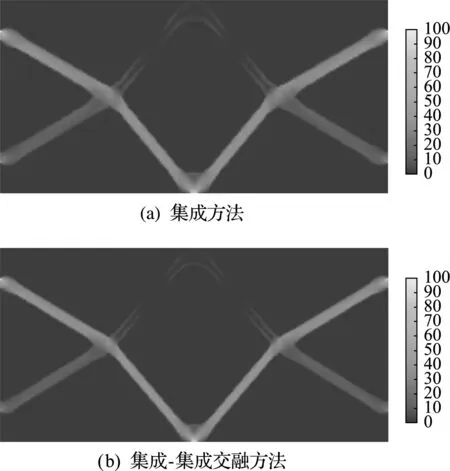
圖8 集成方法與集成-集成交融方法的最優時工況2的Mises應力分布

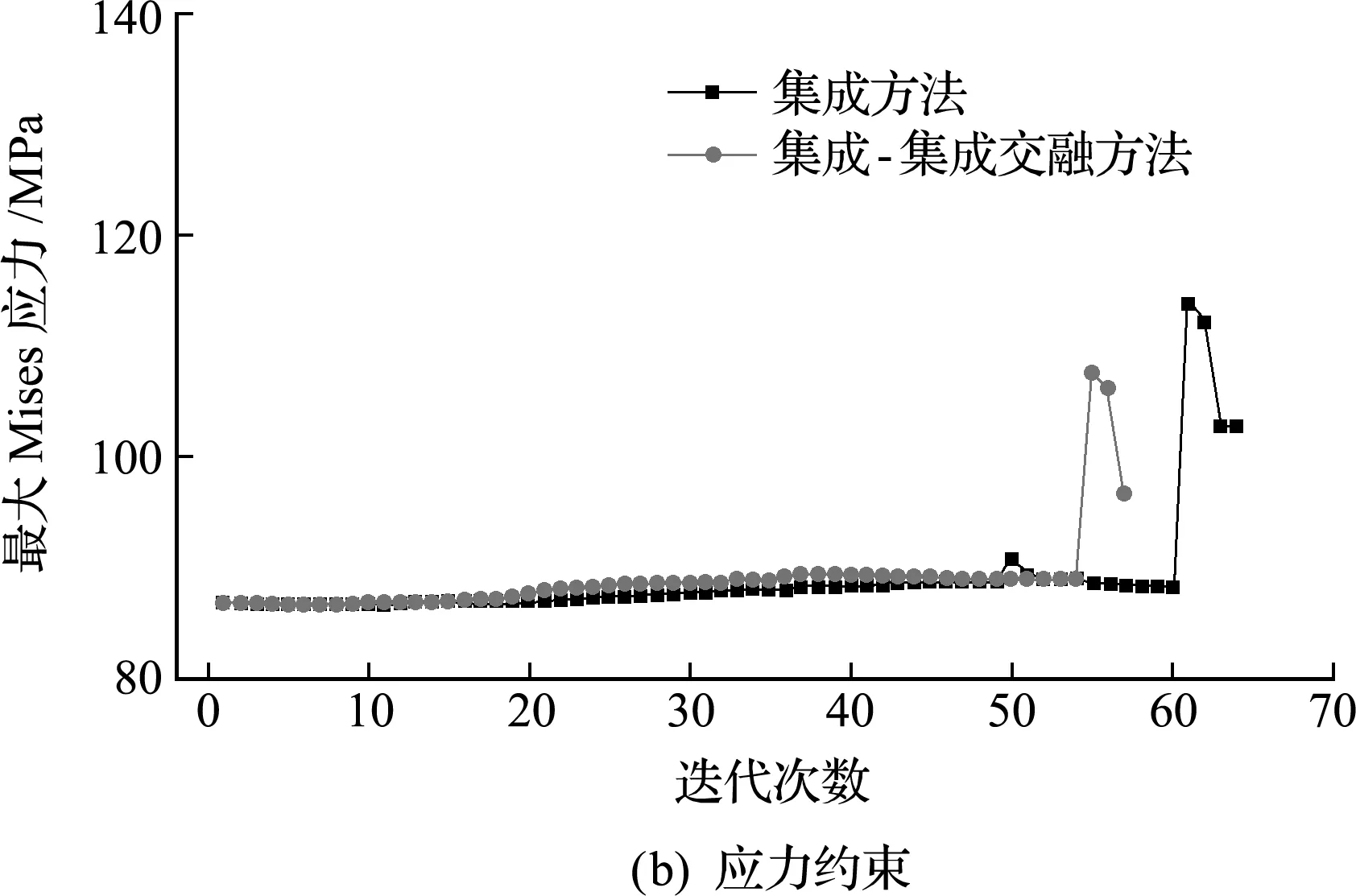
圖9 集成方法與集成-集成交融方法優化過程目標及約束對比

6.3 五次超靜定梁的疲勞約束拓撲優化

如圖10所示，材料性能為E=2.1×105MPa，泊松比ν=0.3，材料對應于循環次數1.0×106的疲勞極限為σs=250 MPa，基結構為 800 mm×200 mm×10 mm的平面體，劃分為400×100個矩形單元。基結構的四個角點皆為雙向約束鉸支座。工況為正弦形式循環載荷F=21000 N且均值為0，相位角為0，作用于圖10基結構的中心點，為了避免應力集中將荷載施加在五個節點上。疲勞壽命約束為大于或等于1.0×105次。Basquin公式中常數值取m=0.10，A=995.3 MPa。

圖10 五次超靜定梁結構的優化模型

Fig.10 Model of structure for analysis and optimization of the statically indeterminate beam

本算例分別以單純分部方法(P解法)及分部-集成交融方法(P -I 解法)求解疲勞壽命約束體積極小化問題。P解法經過36次迭代收斂，最優體積比為0.488，最大疲勞壽命為99141次。P -I 解法經過26次迭代收斂，最優體積比為0.483，最大疲勞壽命為100675次。兩種方法得到的最優拓撲如 圖11 所示，對應的疲勞壽命以10為底的對數分布如圖12所示，目標及約束的迭代歷史曲線對比如 圖13 所示。相比P解法，P -I 解法的迭代次數減少了10次，收斂更快。

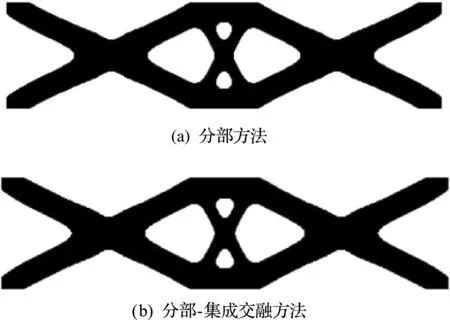
圖11 單純分部方法與分部-集成交融方法得到的最優拓撲

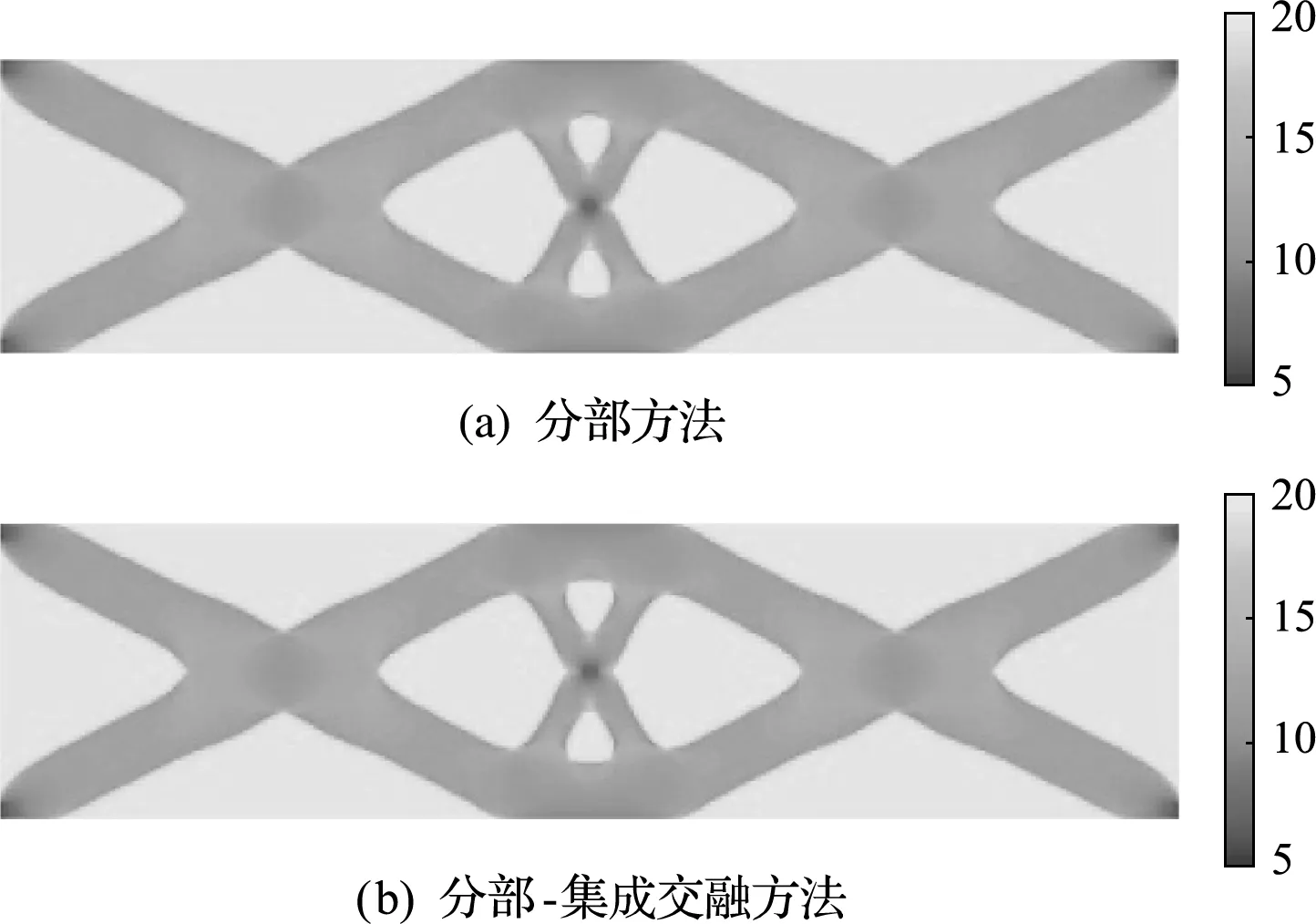
圖12 分部方法與分部-集成交融方法的最優時疲勞壽命分布

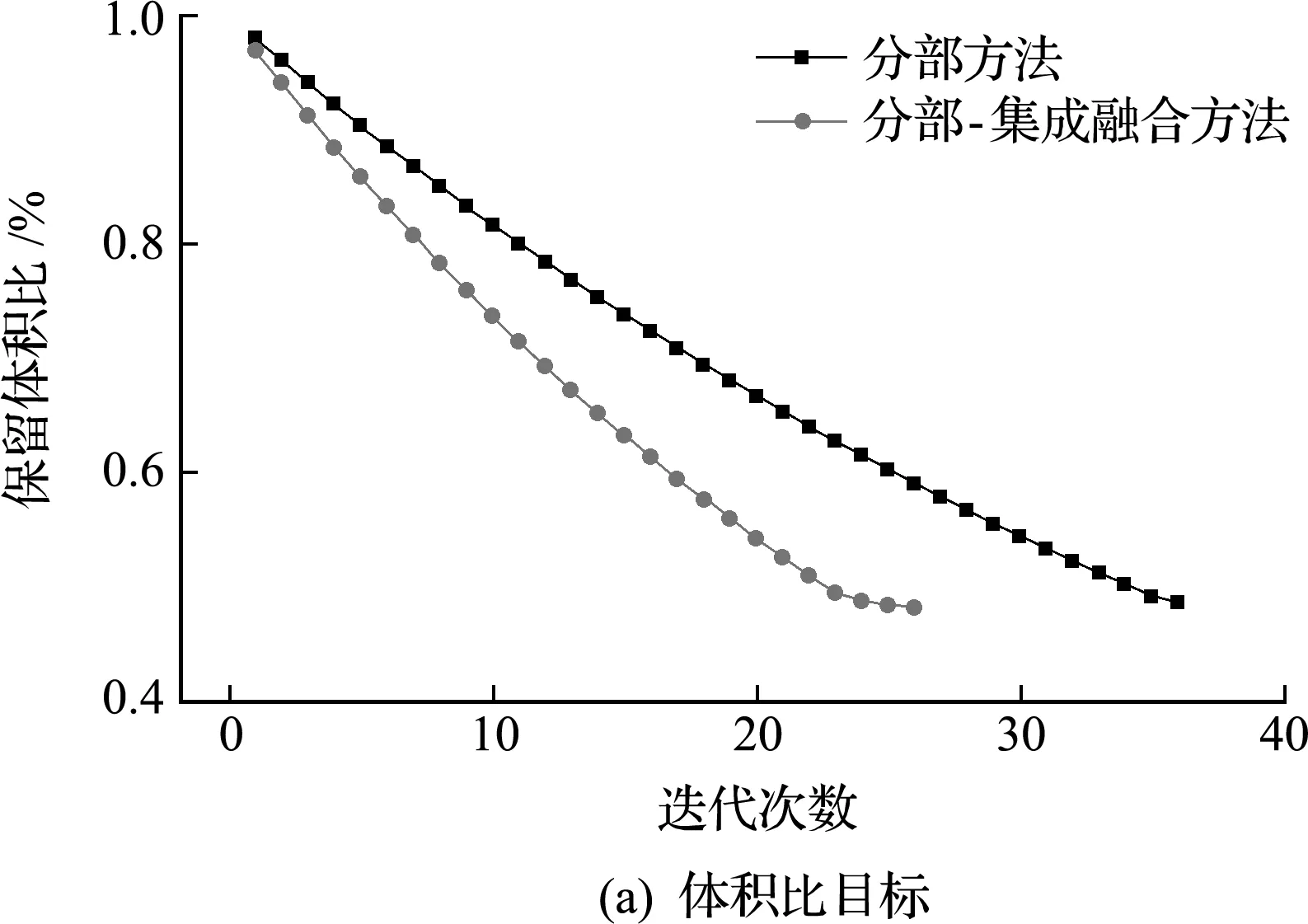
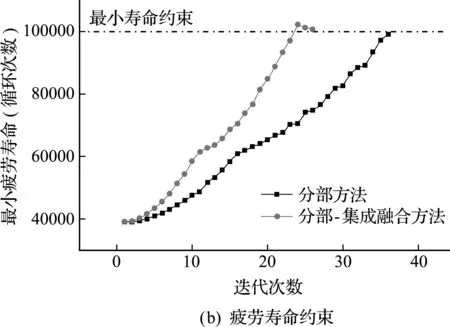
圖13 分部方法與分部-集成交融方法優化過程目標及約束對比

7 結 論

類比對應力約束的處理措施，給出疲勞約束對應的過濾函數。仿應力約束問題的滿應力準則，介紹了滿疲勞設計準則。仿應力約束問題的化整方法的全局化應力約束，給出了疲勞約束化整方法的全局化疲勞約束。基于倒壽命的概念，實現了疲勞約束與應力約束的規格統一。對結構疲勞約束與應力約束的局部性能約束問題，梳理了3種單目標優化方法，闡述了新提出的由單目標與多目標交替迭代的3種交融優化方法。數值算例表明，交融解法的求解效率，比單目標解法更加有效，這是每次結構分析之后做了兩次尋優的必然結果。

致謝:碩士生張譯文同學參加了算例計算。

參考文獻(References):

[1] 錢令希.工程結構優化設計[M].北京：水利電力出版社,1983.(QIAN Ling-xi.OptimizationDesignforEngineeringStructures[M].Beijing:Water Conservancy and Electric Power Press,1983.(in Chinese))

[2] 隋允康.建模·變換·優化:結構綜合方法新進展[M].大連：大連理工大學出版社,1996.(SUI Yun-kang.ModelingTransformaionandOptimzation:NewDevelopmentofStructuralSsynthesisMethod[M].Dalian:Dalian University of Technology Press,1996.(in Chinese))

[3] 隋允康,葉紅玲.連續體結構拓撲優化的ICM方法[M].北京:科學出版社,2013.(SUI Yun-kang,YE Hong-ling.ContinuumTopologyOptimizationICMMethod[M].Beijing:Science Press,2013.(in Chinese))

[4] Sui Y K,Peng X R.Modeling,SolvingandApplicationforTopologyOptimizationofContinuumStructures,ICMMethodBasedonStepFunction[M].Elsevier,2018.

[5] 隋允康，葉紅玲，彭細榮.應力約束全局化策略下的連續體結構拓撲優化[J].力學學報，2006,38(3):364-370.(SUI Yun-kang,YE Hong-ling,PENG Xi-rong.Topologicaal optimization of continuum structure under the strategy of globalization of stress constraints [J].ChineseJournalofTheoreticalandAppliedMechanics,2006,38(3):364-370.(in Chinese))

[6] Schmit L A.Structural design by systematic synthesis[A].Proceeding of Conference on Electronic Computation,ASCE[C].New York， 1960.

[7] Shanley F R.Weight-StrengthAnalysisofAircraftStructures[M].New York,1960.

[8] Spunt L.OptimumStructuralDesign[M].New Jersey,1971.

[9] Yang R J,Chen C J.Stress -based topology optimization[J].StructuralOptimization,1996,12(2):98-105.

[10] 隋允康，張學勝，龍連春.應力約束處理為應變能集成的連續體結構拓撲優化[J].計算力學學報,2007,24(5):602-608.(SUI Yun-kang,ZHANG Xue -sheng,LONG Lian-chun.ICM method of the topology optimization for continuum structures with stress constraints approached by the integration of strain energies[J].ChineseJournalofComputationalMecha-nics，2007,24(5):602-608.(in Chinese))

[11] 隋允康，鐵 軍.結構拓撲優化ICM顯式化與拋物型凝聚函數對于應力約束的集成化[J].工程力學，2010,27(2):124-133.(SUI Yun-kang,TIE Jun.The ICM explicitation approach to the structural topology optimization and the integrating approach to stress constraints based on the parabolic aggregation function [J].EngineeringMechanics,2010,27(s2):124-133.(in Chinese))

[12] París J,Navarrina F,Colominas I,et al.Improvements in the treatment of stress constraints in structural topology optimization problems [J].JournalofComputationalandAppliedMathematics,2010,234(7):2231-2238.

[13] Luo Y J,Wang M,Kang Z.An enhanced aggregation method for topology optimization with local stress constraints[J].ComputerMethodsinAppliedMechanicsandEngineering,2013,254(2):31-41.

[14] 隋允康，彭細榮，葉紅玲，等.互逆規劃理論及其用于建立結構拓撲優化的合理模型[J].力學學報，2019,51(6):1-9.(SUI Yun-kang，PENG Xi-rong，YE Hong-ling，et al.Reciprocal programming theory and its application to establish a reasonable model of structural topology optimization[J].ChineseJournalofTheoreticalandAppliedMechanics,2019,51(6):1940-1948.(in Chinese))

[15] 鐵 軍,隋允康,彭細榮.互逆規劃的拓寬和深化及其在結構拓撲優化的應用.力學學報,2020,52(6):1822-1837.(TIE Jun,SUI Yun-kang,PENG Xi-rong.Widening and deepening of reciprocal programming and its application to structural topology optimization[J].ChineseJournalofTheoreticalandAppliedMe-chanics，2020，52(6)：1822-1837.(in Chinese))

[16] Sui Y K,Peng X R.Explicit model of dual programming and solving method for a class of separable convex programming problems[J].EngineeringOptimization,2019,51(9):1604-1625.