結構多源不確定性反問題的流形學習求解方法

韓 旭*1,， 劉 杰， 陳金龍

(1.河北工業大學 機械工程學院，天津 300401；2.湖南大學 機械與運載工程學院，長沙 410082)

1 引 言

工程反問題是從演化結果出發，根據觀測數據或期望達到的性能來探求結構的內部規律或其受外部影響[1]。近幾十年來，隨著傳感與測量技術的進步，以及數值模擬與智能計算方法的涌現，工程反問題理論與方法的研究已有長足發展，為準確獲取傳統試驗測試難以確定的結構參量以及實現復雜工程結構的高精度建模與分析提供了有效途徑。工程反問題方法研究主要集中于確定性反問題，即計算反求過程中的測量響應、結構模型和反求參量均在確定性框架下進行處理。然而，實際工程結構在幾何、材料、工藝、載荷、測量響應和模型偏差等方面不可避免地存在不確定性因素[2-4]。為此，科學合理地度量工程反問題的復雜不確定性，實現多源不確定性下未知結構參量的高效計算反求，對于反問題的理論發展和工程應用都具有重要意義。

根據不確定性的來源不同，工程不確定性反問題可概括分為測量不確定性反問題和模型不確定性反問題。對于測量不確定性反問題，以發展成熟的概率理論為基礎，早期主要發展了最大似然估計方法和貝葉斯反求方法。最大似然估計方法[5]是根據已知測量的統計信息，建立最大似然估計優化模型，以獲取能夠以較高概率產生測量數據的反求參量。為了充分利用先驗信息，Tarantola[6]在貝葉斯框架下較為系統地探討了模型參量識別的不確定性反問題理論和求解方法。Jiang等[7]發展了基于高斯過程模型的參量更新方法，增強了參量后驗概率的可辨識性。但目前貝葉斯反問題的求解還依賴于計算耗時的馬爾科夫鏈蒙特卡洛方法。為了克服不確定性反問題涉及的多層嵌套瓶頸，有效提高計算反求的效率和工程實用性，近年來基于不確定性傳播和計算反求的解耦策略引起學者關注。Liu等[8,9]建立了面向任意概率分布的結構不確定性正向傳播與反向識別統一框架，并將測量不確定性反問題轉化為多個確定性反問題進行求解。另外，為了處理小樣本、認知不確定性下的參量識別反問題，以非概率凸集度量為基礎的計算反求方法有待發展。Jiang等[10]提出了區間反問題的概念和求解方法，實現了層合板結構材料特性參量的區間不確定性識別。Wang[11]考慮非精確信息發展了基于證據理論的結構參量識別方法。

對于模型不確定性反問題，不僅需利用已知測量信息和結構模型來實現未知參量的計算反求，而且還需要定量化分析結構建模本身的不確定性對反求參量的影響。由于求解過程的復雜性，目前關于模型不確定性反問題的研究相對較少。Du[12]提出了基于序列可靠性分析的不確定性反求方法，實現了建模不確定性下結構未知參量概率分布的有效估計。Liu等[13,14]利用隨機結構之間的相似性，提出了基于相似系統分析和點估計的模型不確定性反問題高效求解方法，實現了模型參量的概率不確定性向反求參量的傳播分析。Liu等[15]發展了區間不確定性結構的動態載荷識別方法，準確穩定地獲取了載荷的不確定性邊界。

事實上，對于實際工程問題中的結構參量反求，更為普遍的是測量不確定性和模型不確定性往往同時并存，這類問題在本文中稱之為多源不確定性反問題。由于不同來源不確定性的耦合作用，以及反問題求解計算的復雜性等，導致很難探明多源不確定性在結構參量識別中的逆向傳遞機理，相關研究目前也鮮有報到。為此，本文針對實際工程中更為普遍存在的多源不確定性反問題進行探索性研究，特別是發展高效的基于混合度量和流形學習的多源不確定性計算反求方法，在實現未知結構參量識別的同時有效量化測量不確定性和模型不確定性對反求參量的綜合影響，提高不確定性反問題的工程實用性。

2 不確定性反問題建模

從系統論的角度而言，結構參量識別反問題是利用已知的測量響應和正問題模型對未知的結構參量進行反求。對于實際工程結構，由于材料或載荷的隨機性、制造或測量的誤差以及物理過程認知不明晰等原因，在測量響應和正問題模型中往往存在各種不確定性因素。不確定性反問題的求解不僅需要實現結構參量的有效識別，而且還需定量化評估不同來源不確定性對參量識別結果的影響，因此是一個涉及結構參量計算反求和不確定性傳播的雙層嵌套復雜求解過程。根據不確定性在系統中出現位置的不同及對反求參量影響的不同，特別是雙層嵌套求解機制的不同，可將結構參量識別的不確定性反問題分為測量不確定性反問題、模型不確定性反問題和二者并存的多源不確定性反問題。

2.1 測量不確定性反問題

結構測量響應不確定性來源于測量誤差的統計或不確定性結構的統計響應。測量不確定性反問題可描述為利用已知的不確定性測量響應和確定性系統模型，對未知的結構參量進行識別，并評價測量不確定性對參量識別影響，其模型可表述為

(1)

式中Z和fZ(Z)為測量響應及其不確定性度量，X和fX(X)為待反求的結構參量及其不確定性度量，F為測量不確定性到反求參量不確定性之間的映射關系，g為結構正問題模型。

測量不確定性反問題的求解可通過不確定性傳播分析和優化反求的迭代來實現。如圖1所示，對于測量不確定性反問題涉及的雙層嵌套求解過程，其內層為結構不確定性傳播，即利用結構正問題模型實現從給定的fX(X)到計算響應不確定性的量化分析；其外層為優化反求過程，即對待反求參量的fX(X)進行優化，使計算響應與測量響應之間的不確定性度量達到匹配。

圖1 測量不確定性反問題的嵌套求解

2.2 模型不確定性反問題

模型不確定性反問題中部分模型參量及其不確定性度量已知，如隨機結構中參量概率分布已知，而部分模型參量未知，需通過有限的測量響應進行反求識別，并評估模型不確定性對反求參量的影響。鑒于此，模型不確定性反問題可表述為

(2)

式中U和fU為結構正問題模型中的不確定性參量及其度量。

事實上，在不確定性參量每一特定的蒙特卡洛采樣下，結構正問題模型可認為是確定的，故可通過大量采樣下的確定性反問題求解及反求參量的統計來實現模型不確定性反問題的求解。基于此思想，模型不確定性反問題也是通過不確定性傳播分析和優化反求的迭代來實現，但其內外層結構與測量不確定性反問題相反。如圖2所示，其內層為在特定不確定性參量樣本點下，進行確定性計算反求獲取相應未知參量的識別結果；其外層為利用不確定性傳播分析方法，實現從模型參量不確定性度量到反求參量不確定性度量的量化分析。

圖2 模型不確定性反問題的嵌套求解

2.3 多源不確定性反問題

對于工程中更為普遍的多源不確定性反問題，在實現未知結構參量反求的同時，需綜合評價測量不確定性和模型不確定性對待參量識別結果的影響，其模型可表述為

(3)

式中fZ(Z)·fU(U)為測量和模型的聯合不確定性度量，且兩類不確定性相互獨立。

通常結構響應可通過多次測量獲取較為充足的響應樣本，故本文采用概率模型來度量測量響應中的隨機不確定性。結構建模過程存在一定的認知局限性，且難以獲取復雜工程結構的模型樣本，本文采用非概率多邊凸集模型[14]來度量結構模型中的不確定性。如圖3所示，以二維不確定性為例，根據少量樣本點可以獲得傳統區間模型

圖3 多邊凸集模型

U∈{ΩI|UL≤U≤UR}

(4)

式中UL和UR為不確定建模參量樣本的上下界。對樣本點數據進行主成分分析，得到特征向量PT，并將其作為樣本數據空間的正交基底，即轉換矩陣。以特征向量對應的基方向構成新的不確定性建模坐標系，并將樣本數據向其投影，得到主成分PCA(Principal component analysis)區間模型

(5)

(6)

多源不確定性反問題求解的基本思想是將不確性反問題轉化為確定性反問題，以實現測量及模型兩類不確定性反問題的解耦。在多邊凸集度量下，對于凸集不確定性模型參量每一特定的蒙特卡洛樣本，結構正問題模型可視為是確定的，則多源不確定性反問題退化為測量不確定性反問題。在概率度量下，求解該測量不確定性反問題可獲得反求參量的一條概率分布函數CDF(Probability distribution function)曲線。如圖4所示，如遍歷整個多邊凸集模型采樣，可獲得一簇CDF曲線，進而可采用CDF曲線的邊界即 P -box 模型來實現多源不確定性反問題識別結果的綜合不確定性量化。

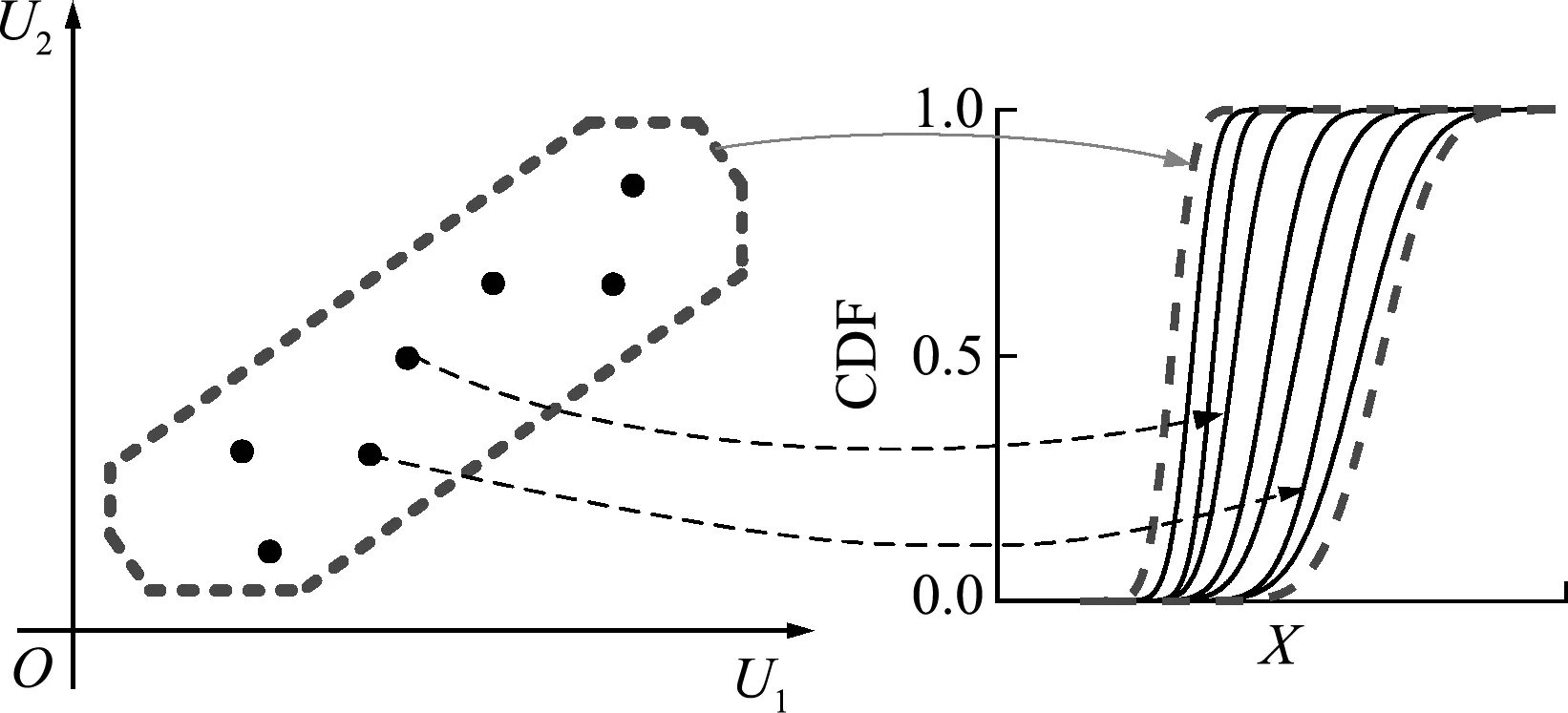
圖4 不確定性模型參量與反求參量CDF間的映射

根據上述分析可知，如圖5所示，多源不確定性反問題的求解是一個復雜的多層嵌套過程，涉及模型不確定性反問題和測量不確定性反求的耦合，并存在迭代求解計算量大的瓶頸問題。

圖5 多源不確定性反問題求解策略

3 基于CDF流形學習的多源不確定性反求方法

由于不確定性模型參量的多邊凸集模型中任意一個樣本點都與反求參量的 P -box 模型中的一條CDF曲線對應，如能構建出二者之間映射關系，則有望快速遍歷整個多邊凸集模型的采樣，獲取反求參量的 P -box 模型。基于此思想，本文提出基于CDF流形學習的多源不確定性反問題高效求解方法。該方法通過建立不確定性模型參量與反求參量CDF間的流形學習映射模型，實現測量響應不確定性反問題與模型不確定性反問題的解耦，從而將多源不確定性反問題轉化為少數幾個測量不確定性反問題，進而將測量不確定性反問題通過降維積分方法又轉化為了少數幾個確定性反問題，以此解決多源不確定性反問題多層耦合嵌套導致的計算量大的難點問題。

3.1 不確定參量與反求參量的CDF流形學習映射

本文方法的重點是建立不確定性模型參量與高維反求參量CDF曲線之間的映射關系。為此，將流形學習方法引入映射模型構建中，將高維CDF曲線轉化為流形空間的低維特征參數，通過建立模型參量與低維特征參數之間的代理模型，實現給定模型參量下反求參量CDF的快速預測。

在多邊凸集模型內對不確定性模型參量進行最優拉丁超立方抽樣，獲取m個樣本點。對于每一樣本點，進行測量不確定性反問題求解，可獲得與之相對應的m條待反求參量CDF曲線。統一將每組CDF曲線進行離散，則可獲得離散維矩陣H。

H=[h1,h2,…,hm]T

(4)

(5)

對協方差矩陣C進行特征值分解，并將特征值按由大到小的順序排列。在保證CDF流形學習映射模型精度的情況下，舍棄貢獻較小的特征值，實現數據降維，即取前k(k?d)階特征值和對應的特征向量。

通過上述分析，可將d維的高維問題轉化為k維的低維問題進行處理，通過低維流形空間中特征向量的線性組合可近似重新構建高維的反求參量CDF，實現給定模型不確定性參量U下對應的反求參量CDF曲線離散向量的快速預測，即

(6)

3.2 基于降維積分的測量響應不確定性反求

3.1節通過流形學習方法將多源不確定性反問題轉化為少數幾個測量不確定性反問題，本節將利用基于衍生的λ-PDF降維積分方法進一步將測量不確定性反問題轉化為少數配置點處的確定性反問題。

對于測量不確定性反問題，待反求參量的概率密度函數PDF(Probability density function)形式未知，即其PDF可能為任意形式。為此，本文采用二階衍生的λ-PDF[18]對未知反求參量的不確定性進行建模，

f(x|b0,b1,b2,λ)=

(7)

κ=Γ(λ+1)/[Γ(0.5)Γ(λ+0.5)]

(8)

式中b0,b1和b2為衍生的λ-PDF的控制參數，Γ(·)為伽馬函數。如圖6所示，二階衍生的λ-PDF可以參數化地表示未知的任意概率密度曲線。

圖6 不同λ下衍生的λ-PDF

可通過匹配計算響應與測量響應的統計矩來反求未知參量的PDF，故基于前四階矩的測量不確定性反問題的目標函數可表示為

(9)

(10)

(11)

(12)

其可以通過二項式定理遞推求解

(13)

(14)

基于此，原系統的統計矩分解為子系統的統計矩進行計算，從而有效提高了不確定性傳播效率。

在實現正向不確定性傳播后，利用優化算法對式(9)進行迭代求解，可實現λ-PDF控制參數的有效反求，進而通過式(7)得到與測量響應概率特征最相匹配的待反求參量的CDF曲線。

3.3 多源不確定性反問題求解流程

本文提出的基于流形學習的多源不確定性反問題求解流程如圖7所示。

圖7 多源不確定性反問題求解流程

(1) 獲取結構不確定性測量響應的概率密度函數和模型參量不確定性的多邊凸集模型。

(2) 在多邊凸集內對模型參量進行最優拉丁超立方采樣。

(3) 對于每個模型參量樣本點，利用降維積分和優化算法進行測量不確定性反問題求解，獲取待反求參量的CDF曲線。

(4) 對步驟(3)獲取的CDF曲線進行流形分析，得到低維流形空間的特征向量和特征參數。

(5) 利用步驟(2)模型參量的樣本點和步驟(4)低維流形空間的特征參數，建立徑向基函數代理模型，并實現從模型參量到反求參量CDF的流形學習映射關系建模。

(6) 基于流形學習映射模型對多邊凸集模型中模型參量的蒙特卡洛樣本進行反求參量CDF預測，并統計獲取反求參量的 P -box 模型。

4 算例分析

4.1 數值算例

考慮如下的數值模型

(14)

式中Z1和Z2為已知的測量響應，分別服從正態分布N(9,1.6)和N(23,2.6)；U1和U2為不確定性模型參量，采用如圖8所示的多邊凸集模型對其不確定性進行度量；X1和X2為待反求參量。

圖8 模型參量樣本點和多邊凸集模型

在不確定性模型參量多邊凸集域內進行最優拉丁超立方采樣，生成40個樣本點。在每個樣本點下通過基于降維積分的不確定性反求方法進行測量響應不確定反問題求解，獲得40條反求參量的CDF曲線。將高維的CDF離散數據進行流形分析，將其轉化為低維流形空間中的特征參數和特征向量，并建立不確定性模型參量與待反求參量CDF之間的流形學習映射模型。為驗證流形學習映射模型準確性，圖9給出了4個模型參量測試樣本點下直接預測的CDF曲線與計算反求的CDF曲線。由對比結果可知，流形學習映射模型獲得的CDF與計算反求獲得CDF幾乎一致，可用該映射模型直接替代耗時的測量不確定性反問題求解過程。

在流形學習映射模型基礎上，通過蒙特卡羅仿真MCS(Monte Carlo simulation)實現多邊凸集度量下模型不確定性反問題的統計求解，快速獲得了待反求參量X的 P -box 邊界。為進一步驗證該方法的準確性，在MCS產生的每一模型參量樣本點進行測量不確定性反問題求解，獲取待反求參量的 P -box 邊界，兩種方法的反求結果如圖9所示。根據對比結果可得，本文提出的基于流形學習的多源不確定性反求方法的反求結果與MCS方法的反求結果基本一致，驗證了本文提出方法的準確性。

圖9 反求結果對比

4.2 渦輪葉片熱力學參數的不確定性識別

航空發動機渦輪葉片和氣體的對流換熱系數對渦輪葉片的溫度場分布有很大的影響，因此，有效識別對流換熱系數對渦輪葉片冷卻系統設計及葉片壽命評估具有重要影響[16]。本算例通過測量葉片表面應力來反求葉片壓力面和吸力面與空氣之間的對流換熱系數。考慮到應力測量結果和渦輪葉片建模的多源不確定性，采用本文提出的不確定性反求方法對流換熱系數進行識別。

圖10所示為渦輪葉片的有限元分析模型，其中兩個實心點為應力測量點。葉片熱力學參數不確定性識別對應的正問題模型可表示為

圖10 渦輪葉片有限元模型

σ=g(h1,h2,ε,λ)

(16)

式中σ=[σ1,σ2](MPa)為兩個測點處的應力，分別服從N(671,1)和N(156.84,2)的正態分布。熱膨脹系數ε(10-61/K)和導熱系數λ(W/(m·K))為不確定性模型參量，對應的多邊凸集模型如圖11所示。h1和h2分別為壓力面和吸力面上的對流換熱系數，為待識別的未知參量。

圖11 參數h1和h2多邊凸集模型

在模型參量多邊凸域內隨機抽取20個樣本點，在每個樣本點處利用基于降維積分的反求方法實現測量不確定性反問題求解，獲得相應的識別參量的CDF曲線。利用流形學習方法，構建模型參量與反求參量CDF之間的映射模型，將熱力學參數的多源不確定性反問題轉化為流形學習映射模型下的不確定性傳播問題。通過蒙特卡羅方法對度量模型參量的多邊凸集不確定性向反求參量不確定性進行傳播分析，獲得渦輪葉片熱力學參數 P -box 邊界。反求結果如圖12所示，由反求得到的 P -box 模型可知，壓力面的對流換熱系數大致分布范圍在[52,70] W/(m2·K)區間內，吸力面的對流換熱系數分布在[35,48] W/(m2·K)，另外圖中CDF對比曲線再次驗證了本文提出方法的準確性。

圖12 反求的對流換熱系數 P -box

5 結 論

本文針對多源不確定性反問題中面臨多層耦合嵌套及大規模計算的難點問題，提出了基于概率-非概率混合度量和流形學習的多源不確定性高效計算反求方法。該方法通過建立模型參量與反求參量CDF之間的流形學習映射模型，以少量的計算成本實現了未知參量的 P -box 模型的高效反求。在反求過程中，通過流形學習實現了測量響應不確定性反問題與模型不確定性反問題的解耦，將多源不確定性反問題轉化為少數幾個測量不確定性反問題；進一步對于測量不確定性反問題，通過降維積分方法又轉化為了少數幾個確定性反問題，從而克服了多源不確定性反問題求解過程多層嵌套導致的反求效率和精度問題，在實現參量識別的同時綜合量化了測量不確定性和模型不確定性對反求參量的綜合影響。

參考文獻(References):

[1] Han X,Liu J.NumericalSimulation-BasedDesign[M].Springer Press,2020.

[2] Elishakoff I,Fang T,Sarlin N,et al.Uncertainty quantification and propagation based on hybrid expe -rimental,theoretical,and computational treatment [J].MechanicalSystemsandSignalProcessing,2021,147:107058.

[3] Luo Y J,Kang Z,Li A.Structural reliability assessment based on probability and convex set mixed mo -del[J].Computers&Structures,2009,87(21-22):1408-1415.

[4] Wu D,Gao W,Song C M,et al.Probabilistic interval stability assessment for structures with mixed uncertainty [J].StructuralSafety,2016,58:105-118.

[5] Fonseca J R,Friswell M I,Mottershead J E,et al.Uncertainty identification by the maximum likelihood method [J].JournalofSoundandVibration,2005,288(3):587-599.

[6] Tarantola A.Popper,Bayes and the inverse problem [J].NaturePhysics,2006,2(8):492-494.

[7] Jiang Z,Apley D W,Chen W.Surrogate preposterior analyses for predicting and enhancing identifiability in model calibration[J].InternationalJournalforUncertaintyQuantification,2015,5(4):341-359.

[8] Liu J,Meng X H,Xu C,et al.Forward and inverse structural uncertainty propagations under stochastic variables with arbitrary probability distributions [J].ComputerMethodsinAppliedMechanicsandEngineering,2018,342:287-320.

[9] Meng X H,Liu J,Cao L X,et al.A general frame for uncertainty propagation under multimodally distributed random variables [J].ComputerMethodsinApp-liedMechanicsandEngineering,2020,367:113109.

[10] Jiang C,Liu G R,Han X.A novel method for uncertainty inverse problems and application to material characterization of composites[J].ExperimentalMe-chanics,2008,48(4):539-548.

[11] Wang C.Evidence -theory-based uncertain parameter identification method for mechanical systems with imprecise information[J].ComputerMethodsinApp-liedMechanicsandEngineering,2019,351:281-296.

[12] Du X P.Inverse simulation under uncertainty by optimization [J].JournalofComputingandInformationScienceinEngineering,2013,13(2):021005.

[13] Liu J,Hu Y F,Xu C,et al.Probability assessments of identified parameters for stochastic structures using point estimation method [J].ReliabilityEngineering&SystemSafety,2016,156:51-58.

[14] Cao L X,Liu J,Xie L,et al.Non-probabilistic polygo -nal convex set model for structural uncertainty quantification[J].AppliedMathematicalModelling,2021,89:504-518.

[15] Liu Y R,Wang L,Qiu Z P,et al.A dynamic force reconstruction method based on modified Kalman filter using acceleration responses under multi-source uncertain samples [J].MechanicalSystemsandSignalProcessing,2021,159:107761.

[16] Abu A O,Eshati S,Laskaridis P,et al.Aero -engine turbine blade life assessment using the Neu/Sehitoglu damage model [J].InternationalJournalofFatigue,2014,61:160-169.