循環對稱結構的多尺度拓撲優化方法

(西北工業大學 航宇材料結構一體化設計與增材制造裝備技術國際聯合研究中心，陜西省空天結構技術重點實驗室，西安 710072)

1 引 言

循環對稱結構是一類在極坐標系下沿圓周方向循環對稱的特殊周期結構，如圖1(a)所示的夾芯點陣薄壁圓筒結構，其輕量化高性能設計在航空航天與機械領域具有重要應用價值。同時，這類結構也廣泛存在于骨骼和植物等自然界生物材料中[1-3]。然而，過去幾十年建立的結構多尺度優化方法主要針對笛卡爾坐標系下周期結構，如圖1(b)所示的夾芯點陣平板結構。其特點為所有點陣微結構單胞均為矩形單胞，可由某一單胞經幾何平移操作獲得。因此，所有單胞微結構均可假設具有相同的等效力學性能，并通過均勻化方法計算結構的宏觀力學響應。由此可見，均勻化方法不僅是計算單胞微結構等效力學性能的關鍵步驟，也是關聯微結構與宏觀性能和實現多尺度優化的橋梁。目前，基于微結構均勻化方法，相繼發展了固體各向同性懲罰方法(SIMP)[4,5]、漸進結構優化方法(ESO)[6,7]和水平集方法(LSM)[8]等微結構拓撲優化方法，同時也促進了功能梯度材料以及考慮尺度效應的微結構多目標優化與拓撲優化研究[9-12]。

圖1 夾芯點陣

本文研究的循環對稱結構多尺度拓撲優化問題具有一定的代表性。與平移周期結構相比，可以發現當循環對稱結構的半徑趨于無窮大時，該結構退化為平移周期結構。因此，如何建立循環對稱結構的多尺度優化方法，從理論上實現兩類周期結構的有機統一，不僅具有重要的工程應用價值，也是本文的科學意義所在。

然而，目前循環對稱結構的拓撲優化仍停留在單一尺度上，即直接對周期微結構[13-18]進行優化。由于缺乏微結構力學性能的均勻化等效，計算效率受到極大挑戰，難以實現大規模循環對稱結構的多尺度優化。Zhang等[19]嘗試將針對平移周期微結構等效的均勻化方法直接應用到循環對稱微結構，并未考慮隨半徑位置以及θ方向變化時單胞微結構性能的不同。Chatzigorgiou等[20,21]提出的改進式均勻化方法可用于循環對稱周期微結構均勻化等效，并通過矩陣變換得到笛卡爾坐標系下相應的均勻化等效性能。然而，該方法需要對不同半徑的單胞進行均勻化，其高昂的計算成本極大限制了應用效果，導致相關工作仍停留在均勻化等效層面上，循環對稱結構多尺度拓撲優化研究仍處于起始階段。

2 循環對稱結構均勻化方法

2.1 循環對稱單胞均勻化等效彈性矩陣計算

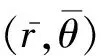
圖2 循環對稱結構

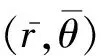
(1)

(2)

表1比較了循環對稱微結構單胞和平移周期微結構單胞的均勻化方法差異。

表1 循環對稱和平移周期微結構的均勻化方法比較Tab.1 Homogenization methods of cyclic symmetrical structure and translational periodic structure

(3)

式中M為二階張量的旋轉矩陣。

(4)

2.2 循環對稱單胞均勻化等效性能的不變性

由表1可知，對于循環對稱單胞，由于微觀算子包含宏觀半徑r，單胞微結構均勻化等效性能與其所在位置對應的宏觀半徑變量相關，理論上應對不同宏觀半徑的單胞分別進行均勻化等效計算。

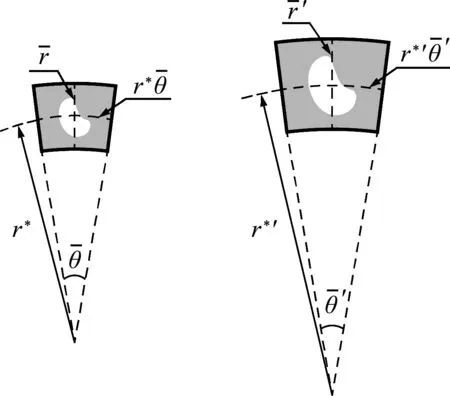
圖3 兩個相似扇形單胞

(5)

(6)

(7)

比較式(6,7)可得

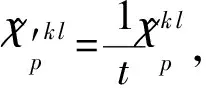
(8)

(9)

式中本文引入單胞無量綱特征參數λ用于描述扇形單胞中心處弧長與邊長之比。其物理意義為，若兩相似單胞的特征參數λ相同，即使宏觀半徑不同，其均勻化等效性能仍然相同。由此可知，圖2所示的循環對稱結構，若單胞微觀邊長與其宏觀半徑呈正比例關系，則其均勻化等效性能保持相同(推導忽略)。

2.3 循環對稱單胞均勻化等效性能的可映射性

受文獻[23，24]關于平移周期單胞存在的映射關系啟發，本文基于特征參數λ建立了循環對稱單胞等效性能計算的映射關系。其重要意義為，對于不同λ的扇形單胞，無需通過式(1)每次重新劃分網格計算其等效性能，只需在標準單胞(λ=1)上計算求解等效性能。其中的基體材料屬性以及最終單胞等效性能通過相應映射計算獲得，由此極大簡化了不同λ取值單胞的均勻化過程。

圖4所示為標準單胞(λ=1)和任意λ取值單胞，參數分別使用上標^和～區分。存在如下幾何關系

圖4 單胞映射變化

(10)

通過理論推導，任意λ取值單胞的均勻化等效性能為

(11)

式中Ti j為映射張量的分量，映射矩陣T為

(i,j=1,2)(12)

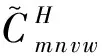
(13)

(14)

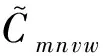
(15)

2.4 循環對稱單胞與平移周期單胞的統一性

考慮圖5所示的循環對稱單胞與平移周期單胞。

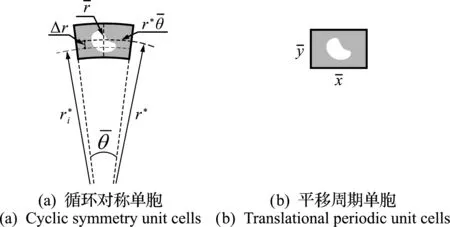
圖5 不同周期單胞

平移周期單胞尺寸分別滿足

(16)

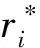
(17)

(18)

即表1兩坐標系下微觀算子等價。因此，當r*→ ∞時，循環對稱單胞與平移周期單胞均勻化等效性能等價。

3 單胞微結構參數化建模與等效

性能插值計算

3.1 單胞微結構的特征驅動參數化建模

基于文獻[25,26]的前期研究工作，本文首次將特征驅動拓撲優化方法應用于循環對稱單胞微結構的多尺度拓撲優化。圖6所示為超橢圓特征，其水平集函數為

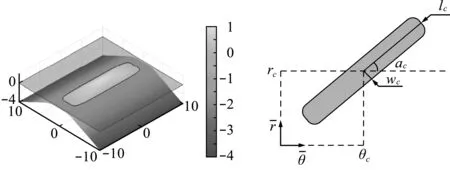
圖6 超橢圓特征水平集函數及其相關設計變量

(19)

(20)

(21)

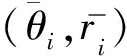
圖7(左)所示為具有最大體積模量和最大剪切模量的兩種平移周期單胞微結構[27]。對其分別采用相同數目的超橢圓特征進行參數化建模，則單胞微結構包含的超橢圓設計變量集合為s。

圖7 兩種典型的微結構

(22)

式中(θc i,rc i,ac i,wc i和lc i)T代表第i個超橢圓設計參數。生成的單胞微結構整體水平集函數可通過所有超橢圓特征水平集函數的布爾運算獲得

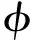
(23)

采用以上最大體積模量和最大剪切模量單胞微結構分別作為初始和最終微結構構型，則任意中間態單胞微結構構型可通過設計變量插值確定。

sκ=sinitial+κ(sfinal-sinitial)

(24)

圖8 由超橢圓特征組成的單胞微結構

(25)

極坐標系下，單胞微結構的體積分數計算式為

(26)

式中H(·)為海維賽德函數。

引入超橢圓寬度比例變量ω用于改變單胞體積分數，則有

sω=ωs,ω=diag(1,1,1,ω,1)

(27)

(28)

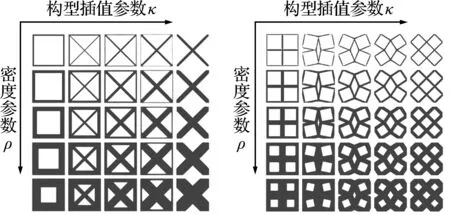
圖9 兩種不同演變形式的參數化微結構

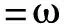
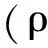
(29)

(30)

3.2 參數化微結構等效力學性能的插值計算

單胞微結構的等效力學性能不僅取決于微結構構型和材料用量，還與其弧邊比特征參數λ緊密相關。為了定量地描述參數化微結構的等效力學性能與微結構控制參數的依賴關系和減少重復計算成本，本文基于函數擬合插值模型[21]構造了等效力學性能與微結構控制參數的近似表達式，具體采用三元四次多項式插值方式描述三個控制參數與等效力學性能的關系。

(31)

式中n=4，βI J L為對應系數。

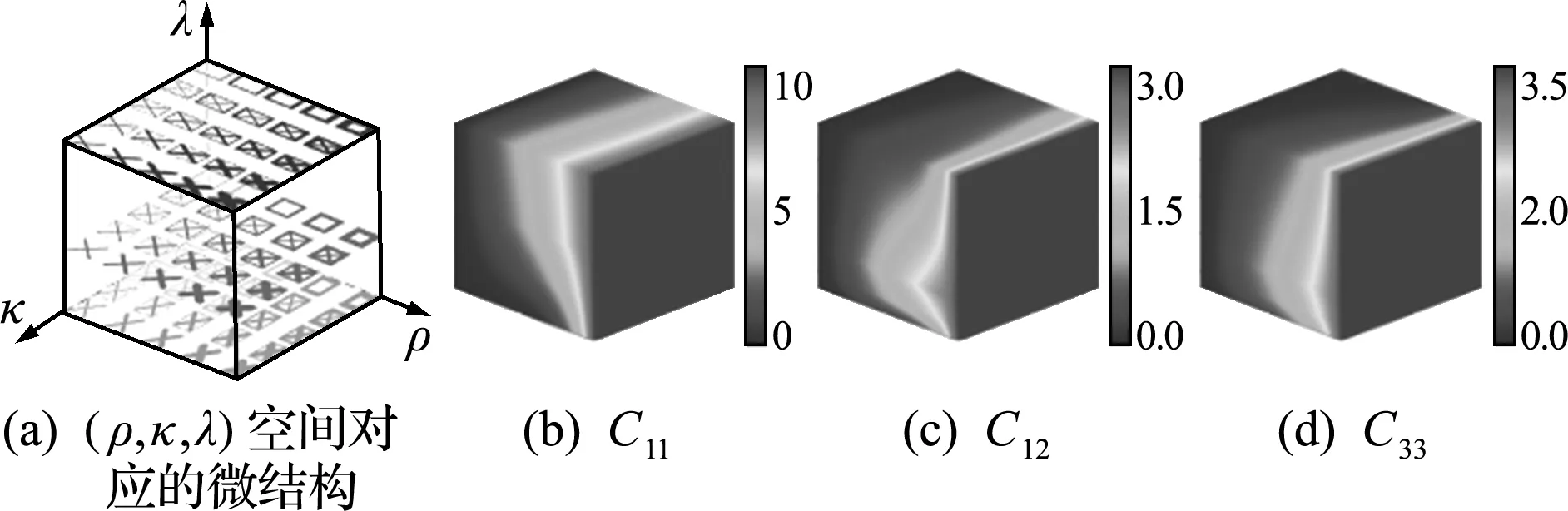
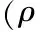
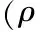
圖11給出了均勻化等效性能C11的剖視圖與λ=1透明截面處的截面視圖。圓圈為原始樣本點均勻化等效數據，均位于擬合曲面附近，具有良好的擬合精度。

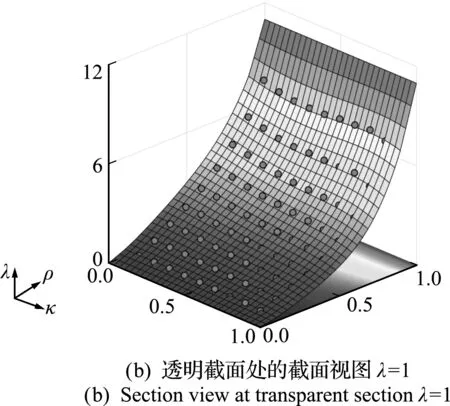
圖11 均勻化等效性能C11

4 密度與插值參數κ空間分布的B樣條參數化建模與優化模型

4.1 基于B樣條參數化的多尺度設計框架

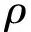
(32)

[sinitial+κ(sfinal-sinitial)]

(33)

如圖12所示，由于相鄰單胞在公共邊界上共享相同參數變量，B樣條可以自動保證微結構的幾何連續性，無需施加任何額外約束。而傳統密度法由于不同單胞微結構的變量離散化定義，即使對微結構進行細分也無法從本質上改變相鄰微結構之間連續性差的問題。

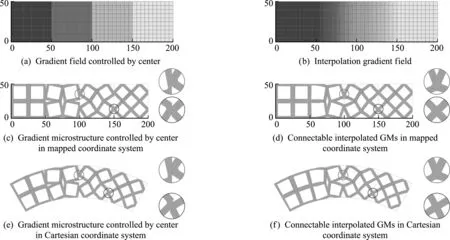
圖12 微結構連接光順性的比較

4.2 循環對稱結構多尺度拓撲優化

研究給定體積約束下結構柔順度最小化問題。對應的數學模型為

min.C=UTKU

(34)

式中λm為中心線半徑處的弧邊比特征參數。

圖13為基于B樣條參數化的循環對稱結構多尺度優化框架。

圖13 循環對稱結構多尺度優化流程

5 數值算例

5.1 曲梁多尺度拓撲優化

圖14所示曲梁左端固支，右下端加載集中力F=1 N。軸線長l=600 mm，寬度h=200 mm，r0=1200/πmm，固體材料楊氏模量E=1 MPa,泊松比為0.3。假設材料用量體分比為50%，曲梁設計域在極坐標系下劃分為20×60個單胞，并填充如圖9(左)所示的參數化微結構，中心線半徑處λm=1。當曲梁半徑R=r0時，曲梁扇形角為90°。隨著R的增大，曲梁的曲率逐漸變小。當R→ ∞時，曲梁的曲率趨近于零并退化為懸臂梁，其均勻化等效性能也與傳統平移周期微結構一致。

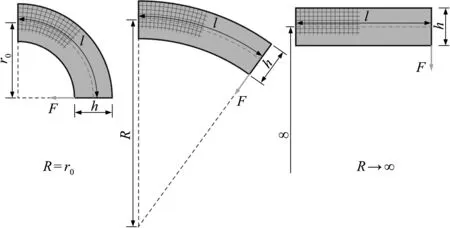
圖14 受集中力的曲梁

針對上述三種情況，將不同R的曲梁均置于相同B樣條參數域中進行拓撲優化，其控制點位置不隨R的變化而發生改變，如圖15所示。

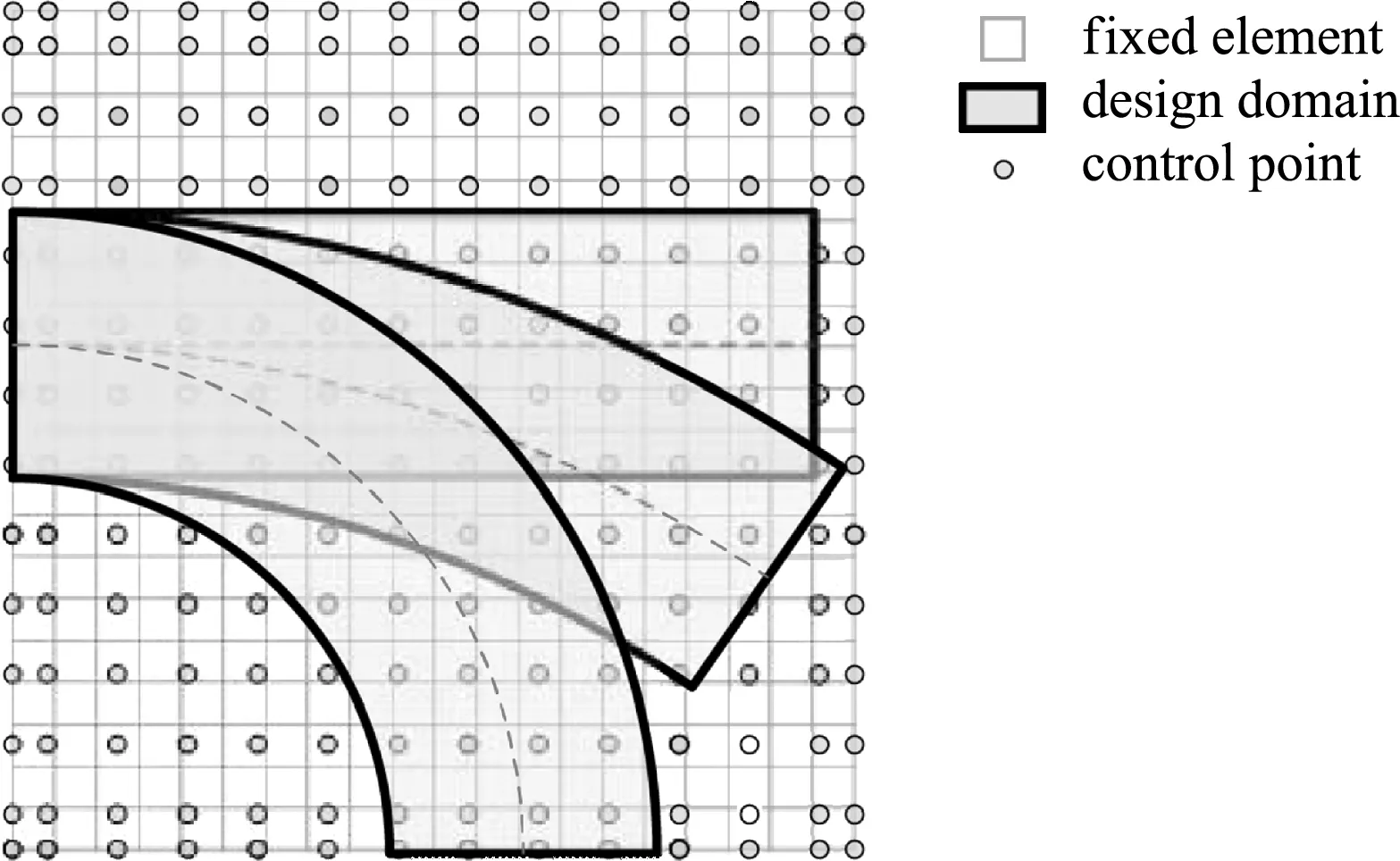
圖15 不同半徑曲梁置于同一個B樣條參數域

為了驗證該方法的正確性，說明平移周期結構是循環對稱結構的特例，取R=1×104r0，使得曲梁接近于懸臂梁的形式。此時，曲梁的弧度約為1.57×10-4，幾乎可忽略不計。多尺度優化結果和迭代曲線如圖16和圖17所示。前者與VCUT水平集方法[29]一致，有效驗證了循環對稱結構多尺度拓撲優化方法的正確性。

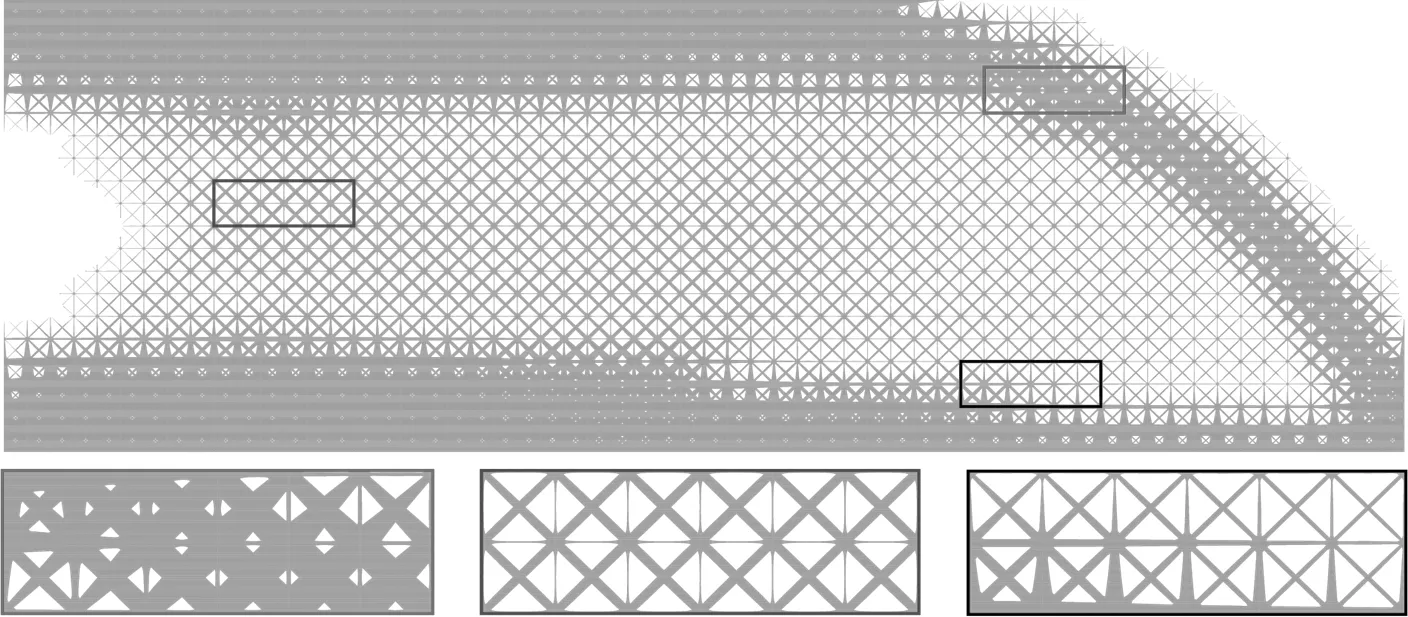
圖16 R=1×104r0的曲梁多尺度優化結果

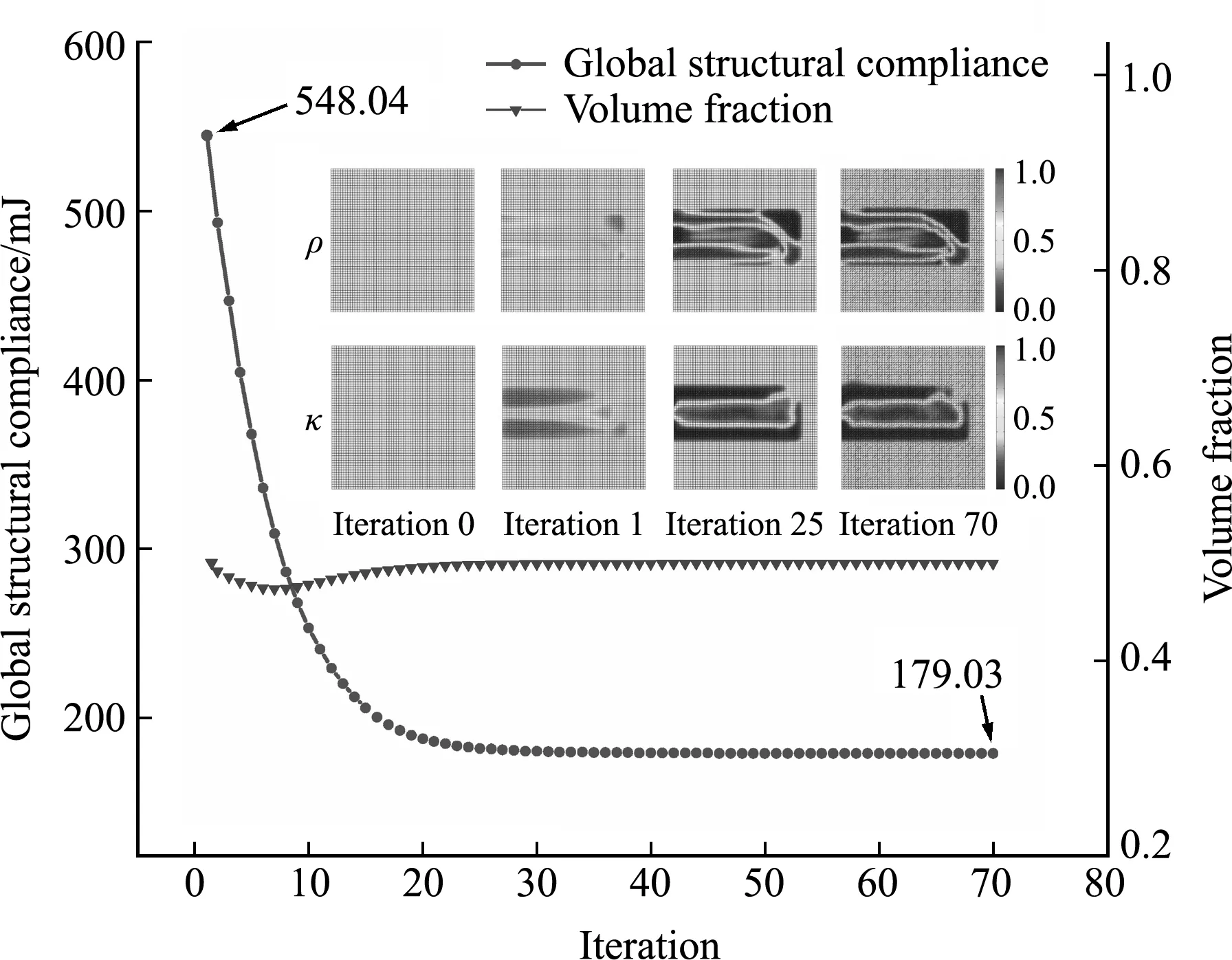
圖17 R=1×104r0時曲梁柔順度和體積分數的迭代曲線

表2給出了不同R下曲梁的多尺度優化結果。

可以發現，材料主要沿上下表面的加載路徑分布，且局部微結構構型與其主應力方向相關，曲梁的上下表面構型參數趨向于0，以橫豎桿為主。在上下主傳力路徑之間，存在一定的過渡結構。從 圖18 可以看出，隨著半徑的增加，柔順度逐漸增加；當半徑趨于無窮大時，逐漸收斂到懸臂梁的柔順度值。

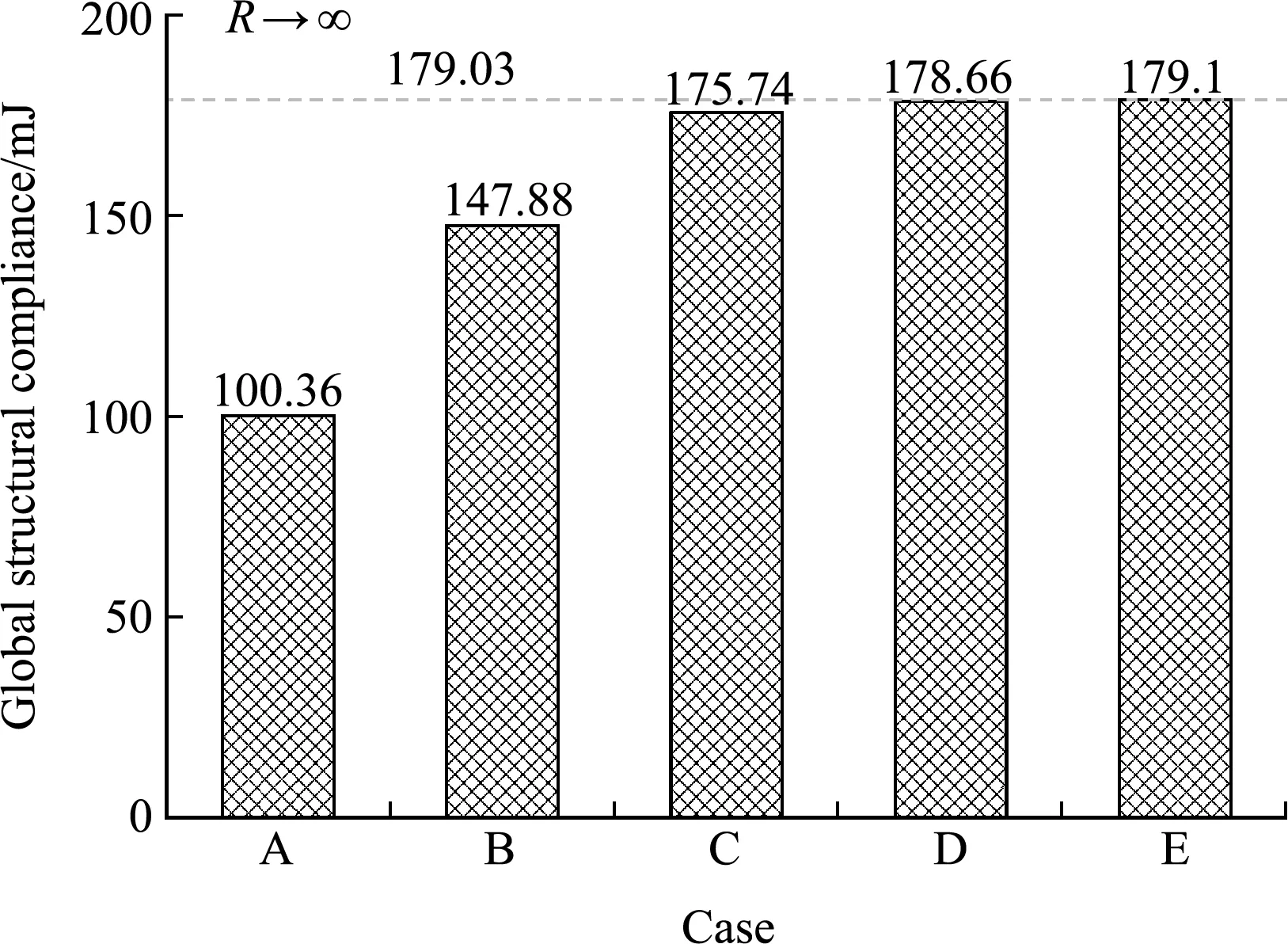
圖18 不同R值曲梁結構柔順度

5.2 圓盤多尺度拓撲優化

該問題著重研究不同循環對稱單胞排列方式、弧邊比參數以及曲率半徑對結構性能的影響。

如圖19(a)所示，圓環內圈固定，圓環外圈施加切向載荷，外徑與內徑之差2(R0-r0)=50 mm。假設材料體積分數限制為40%，基體材料楊氏模量E=10 GPa，泊松比為0.3。圖19(b，c)分別給出了等間距排列單胞和等比例排列單胞。最初將圓盤劃分為6×54個單胞，優化過程中徑向層數保持不變，圓周方向的數目與λm相關。本算例假定r0分別為15 mm,25 mm,50 mm,75 mm，λm的初始值分別為0.54,1.01,1.69,2.36。

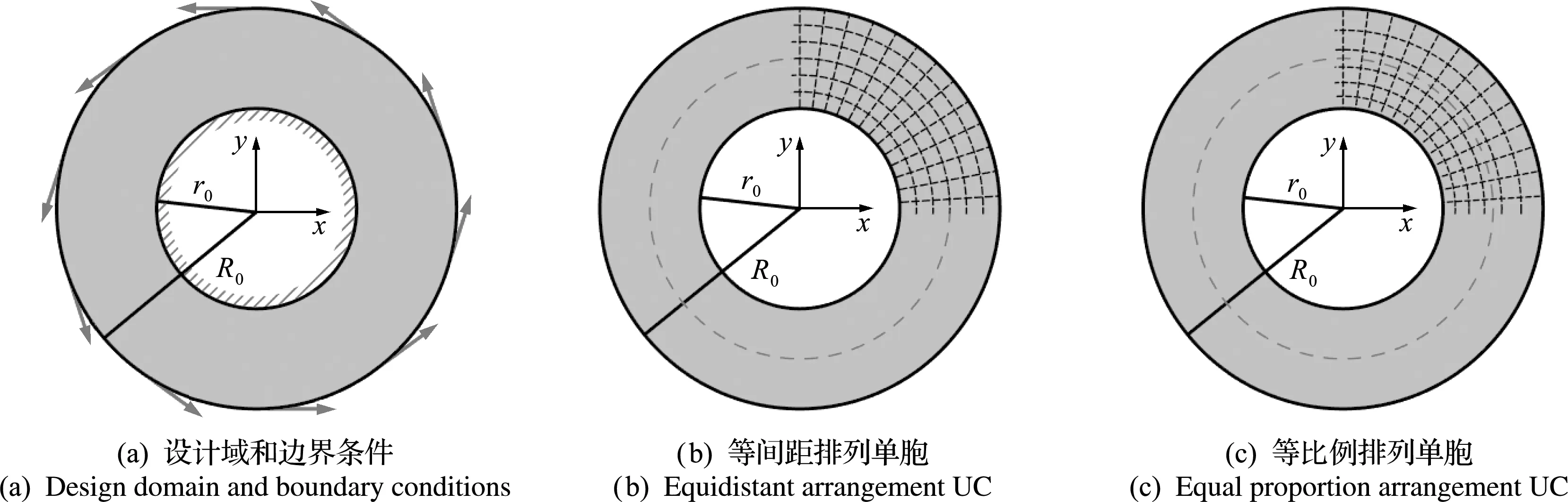
圖19 圓盤問題

對于等間距排列單胞，位于宏觀坐標(r,θ)的微結構弧邊比特征參數λ與中心線弧邊比特征參數λm存在如下關系，

λ=2r/(r0+R0)λm

(35)

等間距排列單胞在不同內徑下的優化設計結果如圖20所示。可以看出，(a) 微結構插值構型參數κ始終接近1，形成X形的微結構。(b)λm總是收斂于1附近，表明具有相同弧長和邊長的扇形單胞更有利于結構優化。(c) 無論內徑長度如何，材料均在內徑處堆積，微結構體積分數從內徑到外徑逐漸減小。 (d) 內徑較小時，內徑和外徑的體積分數變化很大。隨著內徑的增加，內徑與外徑的體積分數差逐漸減小。

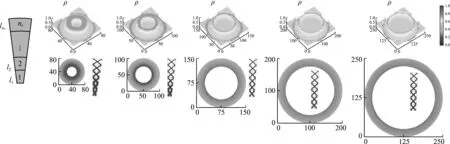
圖20 等間距排列單胞在不同內徑下的優化設計結果

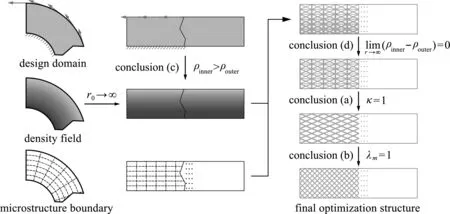
圖21 內徑趨于無窮大時的結構演化

同樣，當r0=15 mm,25 mm,50 mm,75 mm且單胞以等比例方式排列時，可以得到如圖22所示與等間距排列單胞相似的優化結果。該排列方式確保參數λ在圓的所有位置均等于中心線處弧邊比參數λm。

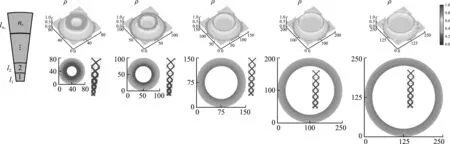
圖22 等比例排列單胞在不同內徑下的優化設計結果

表3比較了相同內徑下不同單胞排列方式對柔順度的影響。柔順度結果表明，等比例排列單胞明顯優于等間距排列單胞。當內徑較小時，這兩種排列結構的柔順度差異很明顯，并在r0=15 mm時二者柔順度降幅達到了6.37%。隨著內徑的增大，二者柔順度的差異逐漸減小。當r0→ ∞時，兩種排列方式之間的差異將不再明顯。因此，在環向剪切載荷作用下，等比例排列比等間距排列具有更大的優勢，在工程中對于受切向載荷的圓筒結構可優先考慮使用等比例排列單胞設計。

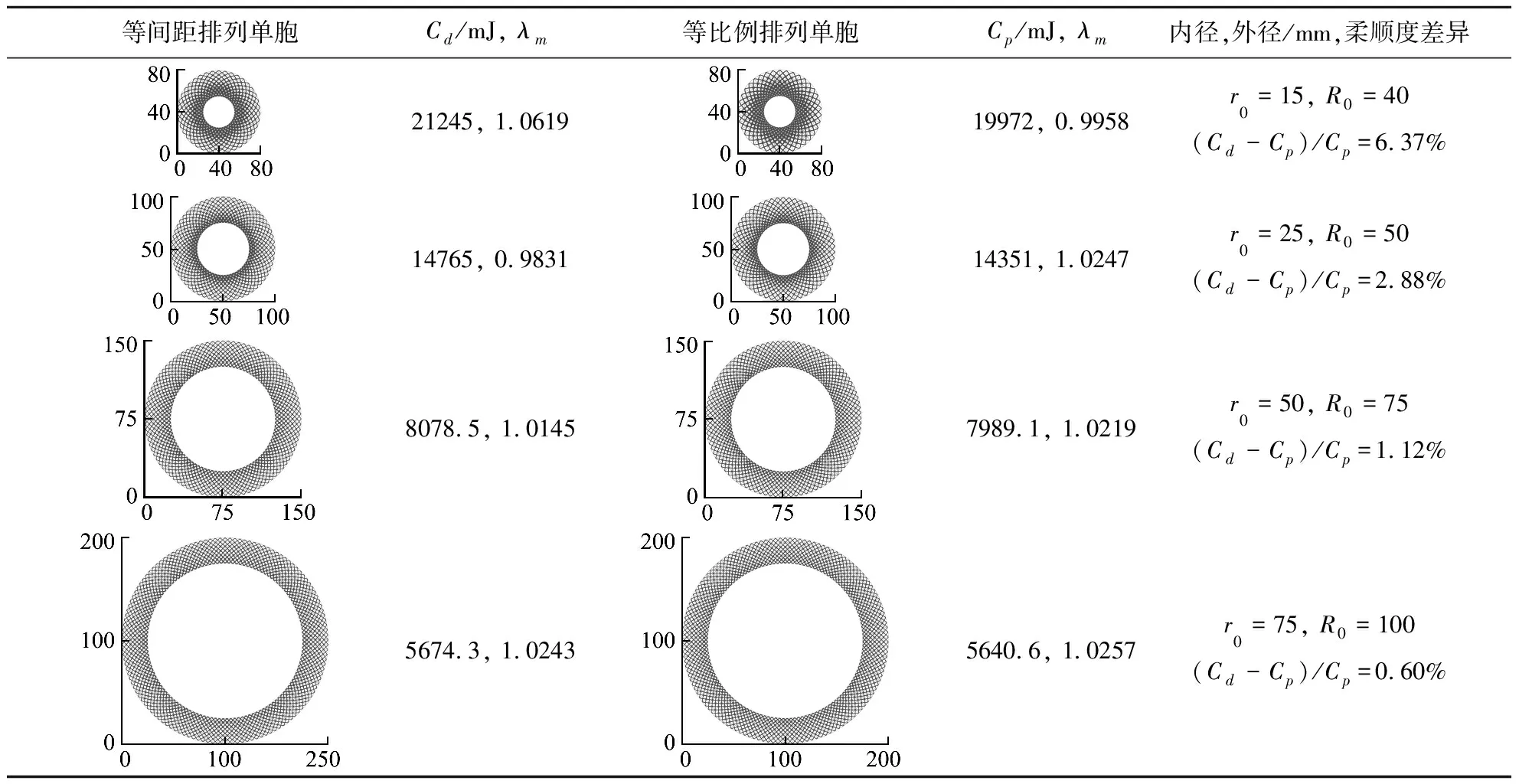
表3 不同半徑不同排列方式柔順度差異Tab.3 Differences in compliance under different radii and different arrangements

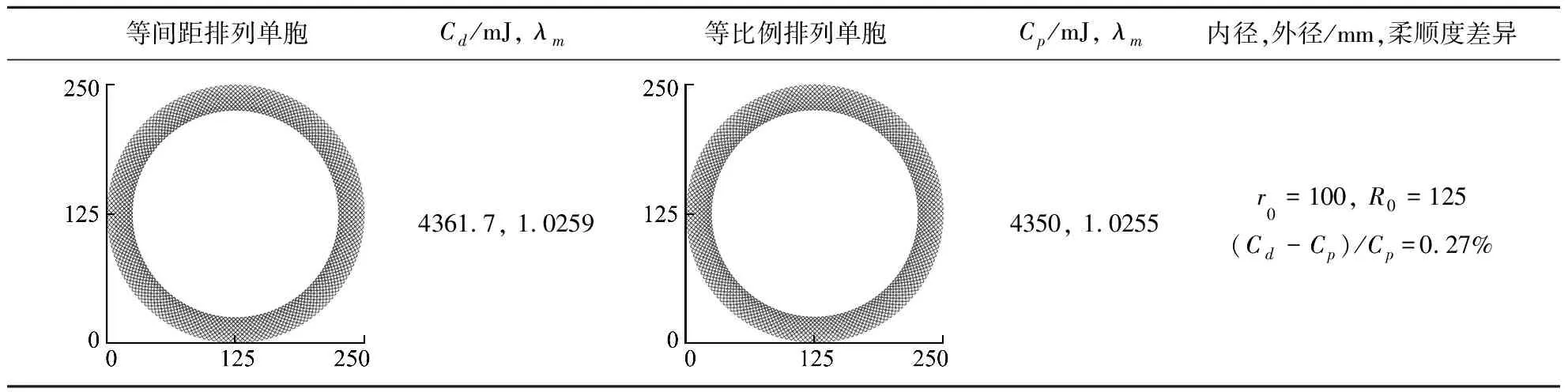
(續表)

6 結 論

本文開展了循環對稱結構多尺度拓撲優化方法研究，提出了用于表征等效性能映射計算的弧邊比特征參數，闡明了循環對稱單胞均勻化等效性能的不變性、可映射性以及與平移周期單胞的統一性，建立了微結構單胞等效性能的三元擬合插值模型與B樣條參數化多尺度設計框架。

算例結果表明，對于受剪切載荷作用的循環對稱結構，等比例單胞排列設計優于等間距單胞排列設計，且當結構半徑趨于無窮大時，循環對稱結構退化為平移周期性結構。

參考文獻(References):

[1] Liu Z Q,Meyers M A,Zhang Z F,et al.Functional gradients and heterogeneities in biological materials:Design principles,functions,and bioinspired applications[J].ProgressinMaterialsScience,2017,88:467-498.

[2] Osorio L,Trujillo E,van Vuure A W,et al.Morphological aspects and mechanical properties of single bamboo fibers and flexural characterization of bamboo/epoxy composites[J].JournalofReinforcedPlasticsandComposites,2011,30(5):396-408.

[3] Chen W J,Zheng X N,Liu S T.Finite -element-mesh based method for modeling and optimization of lattice struc-tures for additive manufacturing[J].Materials,2018,11(11):2073.

[4] Bends?e M P,Sigmund O.Material interpolation schemes in topology optimization [J].ArchiveofApp-liedMechanics,1999,69(9-10):635-654.

[5] Sigmund O.Tailoring materials with prescribed elastic properties[J].MechanicsofMaterials,1995,20(4):351-368.

[6] Xia L,Breitkopf P.Recent advances on topology optimization of multiscale nonlinear structures[J].ArchivesofComputationalMethodsinEngineering,2017,24(2):227-249.

[7] Radman A,Huang X,Xie Y M.Topology optimization of functionally graded cellular materials[J].JournalofMaterialsScience,2013,48(4):1503-1510.

[8] Li H,Luo Z,Gao L,et al.Topology optimization for functionally graded cellular composites with metamaterials by level sets [J].ComputerMethodsinApp-liedMechanicsandEngineering,2018,328:340-364.

[9] 邱克鵬,張衛紅.功能梯度材料結構拓撲優化設計研究[J].西北工業大學學報,2010,28(6):851-857.(QIU Ke -peng,ZHANG Wei-hong.Improving topo -logical design of FGM (functionally graded material) structure[J].JournalofNorthwesternPolytechnicalUniversity,2010,28(6):851-857.(in Chinese))

[10] Wang Y Q,Zhang L,Daynes S,et al.Design of graded lattice structure with optimized mesostructures for additive manufacturing [J].Materials&Design,2018,142:114-123.

[11] 孫士平,張衛紅.多相材料微結構多目標拓撲優化設計[J].力學學報,2006,38(5):633-638.(SUN Shi-ping,ZHANG Wei-hong.Multiple objective topology optimal design of multiphase microstructures[J].ChineseJournalofTheoreticalandAppliedMe-chanics,2006,38(5):633-638.(in Chinese))

[12] 張衛紅,駱金威,戴高明,等.周期性多孔材料等效剪切模量與尺寸效應研究[J].力學學報,2011,43(1):144-153.(ZHANG Wei-hong,LUO Jin-wei,DAI Gao-ming,et al.Numerical predictions of effective shear modulus and size effect for periodic cellular materials [J].ChineseJournalofTheoreticalandApp-liedMechanics,2011,43(1):144-153.(in Chinese))

[13] Tang Y L,Dong G Y,Zhao Y F.A hybrid geometric modeling method for lattice structures fabricated by additive manufacturing[J].TheInternationalJournalofAdvancedManufacturingTechnology,2019,102(9-12):4011-4030.

[14] Dedè L,Borden M J,Hughes T J R.Isogeometric analysis for topology optimization with a phase field model[J].ArchivesofComputationalMethodsinEngineering,2012,19(3):427-465.

[15] Moses E,Fuchs M B,Ryvkin M.Topological design of modular structures under arbitrary loading[J].StructuralandMultidisciplinaryOptimization,2002,24(6):407-417.

[16] Gao T,Zhang W H.Topology optimization involving thermo -elastic stress loads[J].StructuralandMultidisciplinaryOptimization,2010,42(5):725-738.

[17] Zuo Z H,Xie Y M,Huang X D.Optimal topological design of periodic structures for natural frequencies[J].JournalofStructuralEngineering,2011,137(10):1229-1240.

[18] Maharaj Y,James K A.Metamaterial topology optimization of nonpneumatic tires with stress and buckling constraints[J].InternationalJournalforNumericalMethodsinEngineering,2020,121(7):1410-1439.

[19] Zhang H K,Wang Y G,Kang Z.Topology optimization for concurrent design of layer-wise graded lattice materials and structures[J].InternationalJournalofEngineeringScience,2019,138:26-49.

[20] Chatzigeorgiou G,Efendiev Y,Lagoudas D C.Homo -genization of aligned “fuzzy fiber” composites[J].InternationalJournalofSolidsandStructures,2011,48(19):2668-2680.

[21] Wang C,Zhu J H,Zhang W H,et al.Concurrent topology optimization design of structures and non-uniform parameterized lattice microstructures[J].StructuralandMultidisciplinaryOptimization,2018,58(1):35-50.

[22] Xu Z,Zhang W H,Gao T,et al.A B-spline multi-para-meterization method for multi-material topology optimization of thermoelastic structures[J].Struc-turalandMultidisciplinaryOptimization,2020,61(3):923-942.

[23] Chatzigeorgiou G,Efendiev Y,Charalambakis N,et al.Effective thermoelastic properties of composites with periodicity in cylindrical coordinates[J].InternationalJournalofSolidsandStructures,2012,49(18):2590-2603.

[24] Li Q H,Xu R,Liu J,et al.Topology optimization de -sign of multi-scale structures with alterable microstructural length-width ratios[J].CompositeStructures,2019,230:111454.

[25] Zhou Y,Zhang W H,Zhu J H,et al.Feature -driven topology optimization method with signed distance function[J].ComputerMethodsinAppliedMecha-nicsandEngineering,2016,310:1-32.

[26] Xu Z,Zhang W H,Zhou Y,et al.Multiscale topology optimization using feature -driven method[J].ChineseJournalofAeronautics,2020,33(2):621-633.

[27] Xia L,Breitkopf P.Design of materials using topology optimization and energy-based homogenization app -roach in matlab[J].StructuralandMultidisciplinaryOptimization,2015,52(6):1229-1241.

[28] Liu S T,Cheng G D,Gu Y,et al.Mapping method for sensitivity analysis of composite material property[J].StructuralandMultidisciplinaryOptimization,2002,24(3):212-217.

[29] Zong H M,Liu H,Ma Q P,et al.VCUT level set method for topology optimization of functionally graded cellular structures[J].ComputerMethodsinAppliedMechanicsandEngineering,2019,354:487-505.