一種基于附加重力場的鑄件拓撲優化方法

馬 晶， 亢 戰

(大連理工大學 工程裝備結構分析國家重點實驗室，大連 116024)

1 引 言

連續體拓撲優化研究可追溯到Cheng等[1]關于實心彈性薄板剛度最大化設計這一近代布局優化的先驅性工作。目前，拓撲優化已發展成為眾多工程設計領域支撐結構創新設計的關鍵技術之一[2,3]。但是，不同制造工藝的約束建模，仍是拓撲優化方法研究關注的一個重要方向。鑄造工藝廣泛應用在汽車機械、航天航空和土木工程等領域的金屬結構及零件制備中。不同類型的鑄造(金屬鑄造、砂型鑄造和熔模鑄造等)對鑄件拓撲和形狀設計提出了不同的限制。本文僅考慮永久性鑄模的工藝約束，要求在凝固后鑄模應可拆卸,而不會損壞鑄件或模具[4]。在不使用型芯的情況下，鑄件滿足一定的幾何特征才能避免脫模時鑄件卡住模具。鑄件的這種可成型條件稱為鑄造約束。

鑄造約束要求鑄件具有兩個特征(圖1)，一為單連通性，即無內部孔洞(internal cavity)；二為可脫模，即無側凹(undercut)。

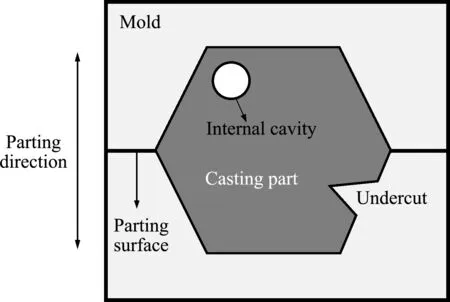
圖1 鑄件脫模

為了將拓撲優化應用在鑄件設計中，學者們針對不同的優化方法提出了多種處理方式，主要分為基于單元密度的方法、基于方向矢量點積的方法和基于標量場的方法三類。

基于單元密度的方法是最早提出的鑄件拓撲優化方法，其直接對設計結構的單元密度進行約束。Zhou等[5]最早提出，通過約束單元密度在脫模方向上單調減小可以抑制內部孔洞和側凹。Harzheim等[6]將該思路應用于基于模擬生物生長規則的密度法，通過限制單元由外向內生長以及僅允許在生長方向上增減單元等，得到了可鑄造的優化解。這種單元密度約束方法還擴展到了多個任意生長方向[7]，并且運用到動力學結構優化中[8]。Gersborg等[9]將每排單元的密度轉化為控制實體和空隙界面位置的單個設計變量。類似地，映射方法(Projection schemes)利用給定的映射函數控制設計的幾何特性。Guest等[10]將鑄造視作銑削的逆過程，給出了一種類似銑削頭形狀的映射函數，同時實現尺寸控制和鑄件優化。Vatanabe等[11]利用映射方法實現了鑄造、鍛造和冷軋等多種工藝約束下的結構拓撲優化。

水平集模型能更清晰描述結構邊界，可用來定義鑄造約束。Xia等[12]最早提出，從可行解出發，約束水平集演進速度方向為分型方向，可以得到可鑄造的優化結構，隨后又將分型方向作為設計變量[13]。Allaire等[14]認為該約束是過度約束，并提出了一種新的點約束形式，限制從邊界點出發沿著分型方向的線與結構相交。Wang等[15]提出了一種積分形式的約束，即要求脫模方向與水平集梯度方向單位矢量的點積在水平集與其偏置形成的窄帶上的積分小于0。Qian[16]采用類似思路，在密度優化法框架下通過約束密度場梯度和指定方向矢量的點積的積分實現了懸垂角和側凹的控制。

第三類方法通過引入虛擬物理場對鑄造約束進行描述。Liu等[17]提出了虛擬溫度場法(VTM)，將孔洞設為自發熱高導熱材料，通過設計域的溫度識別增材制造結構的封閉孔，并在后續工作中通過約束人為設定的最高溫度實現脫模約束[4]。受此啟發，Wang等[18]提出了基于靜電場的鑄造約束方法，同時實現了分型面的控制。在這兩種基于標量場的方法中，無論是溫度場還是靜電場分析都需要求解與位移場分析不同的偏微分方程。

本文提出一種基于附加重力場的鑄造約束方法，利用逆結構的柔順性函數，將內孔及側凹抑制表達為柔順性這一積分量的約束，從而實現鑄件的拓撲優化。該方法的優點是，只需基于位移場的解構造單個鑄造約束，并且無需計算鑄件邊界法向方向，便于數值實現。

2 附加重力場方法

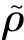
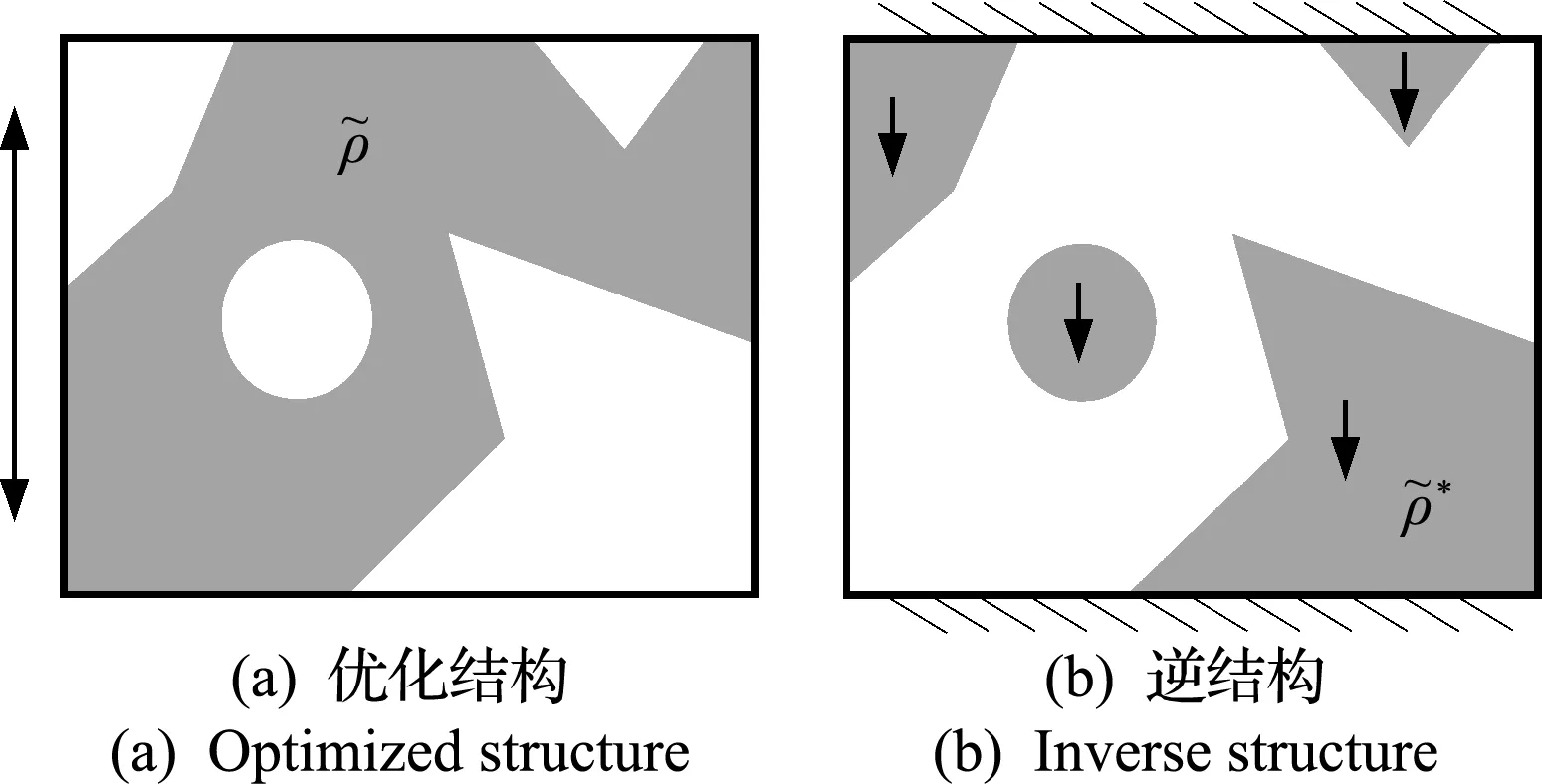
圖2 優化結構及其逆結構

附加重力場方法是利用逆結構的力學解對優化結構的可鑄造性進行量化，逆結構與待優化結構的位移場是獨立求解的。逆結構的部分邊界固定，承受由其相對密度決定的附加重力載荷。逆結構可以類比于模具，而附加重力場方法會使逆結構中不可脫模的部分產生較大的變形。固定邊界和重力載荷方向由預定的分型方向決定，其中分型(脫模)方向即模具移除的方向；固定的邊界可以承受載荷，即模具可以沿著該邊界垂直向外移除。如 圖2 所示，以上下分型設計為例，對上下邊界進行固定，并施加豎直向下的重力載荷。同理，若希望鑄件左右分型，則固定左右邊界并施加橫向的重力載荷。

需要指出的是，本文沒有指定分型面，只給定了分型方向，且要求分型方向與設計域邊界垂直。以圖2(b)的逆結構為例，左上角部分可以向上或者向左脫模，但是內部孔洞和右下角的部分在上下和左右方向都不可脫模。當設定單個脫模方向的時候，與其固定邊界相對的邊界就是分型面(可參見4.2節)；當設定多個脫模方向時，優化結果的分型面不一定是平面。

2.1 無內孔約束

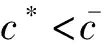
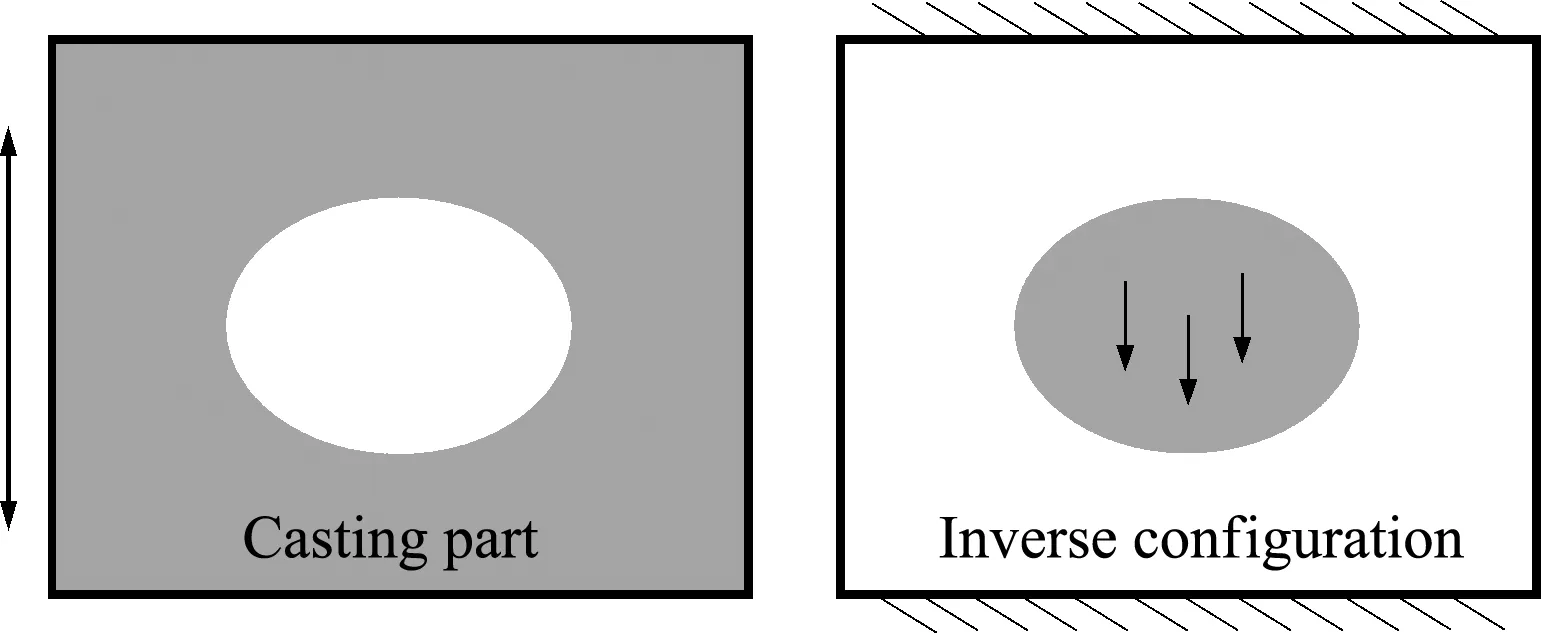
圖3 含內孔鑄件及其逆結構

2.2 無側凹約束

如圖4所示，類比VTM[4]，本文引入參數α<1，令逆結構的材料剪切模量G*=αG0，G0為各向同性材料的剪切模量。

圖4 有側凹的鑄件及其逆結構

3 鑄件拓撲優化

3.1 材料插值

(1)

式中Emin和E0分別為弱材料和結構材料的楊氏模量,q為懲罰因子，本文取為3。

3.2 優化列式

本文以最小化結構柔順性為目標，對鑄件進行拓撲優化。考慮的拓撲優化數學模型如下，

(2)

結構的剛度陣、逆結構的剛度陣和載荷向量分別為

(3)

為了避免棋盤格并減少灰度單元，得到清晰的拓撲結果，本文采用密度過濾以及保體積的 Hea-viside過濾[21]。密度過濾表達式為

(4)

其中權重w(xi)=R-‖xi-xe‖，R為過濾半徑，Ne={i|‖xi-xe‖≤R}為以單元e為中心的過濾半徑內包含的單元。

物理密度表達為

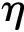
3.3 靈敏度分析

采用伴隨法可得到柔順性對于設計變量的靈敏度

(5)

經過類似的推導可以得到鑄造約束的靈敏度,

(6)

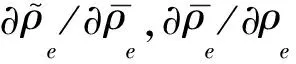
4 數值算例

4.1 二維結構算例

4.1.1 平面梁結構的優化

圖5給出了左角點受力的某平面梁結構。

圖5 平面梁結構

表1 不同約束下的平面梁優化結構

Tab.1 Optimal structures of planar beam

under different constraints

Case 1Case 2Case 3Case 4Topology designCompliance78.84130.77168.70108.21NotesWithout casting constraintα=1,f?yα=0.1,f?yα=1,f?x

圖6給出了Case 2結構優化的迭代歷史，Heaviside過濾的斜率β增加時，目標和約束值會出現突變，隨著結構逐漸清晰，迭代趨于穩定。考慮鑄造約束的三種結果都滿足約束，但結構柔順性有明顯差異。引入了弱剪切條件之后，逆結構中與左邊界相連的部分(圖6(b))明顯減小。這是由于逆結構中該部分弱剪切材料受到向下的重力會產生較大的剪切變形，而與上下邊界相連的部分不會受此影響。

圖6 平面梁結構Case 2的優化迭代歷史

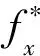
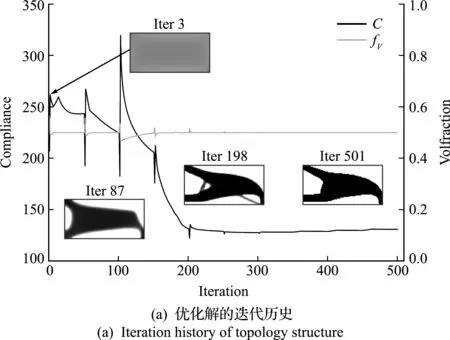
表2 三種構型的逆結構在不同的載荷和剪切模量下的柔順性

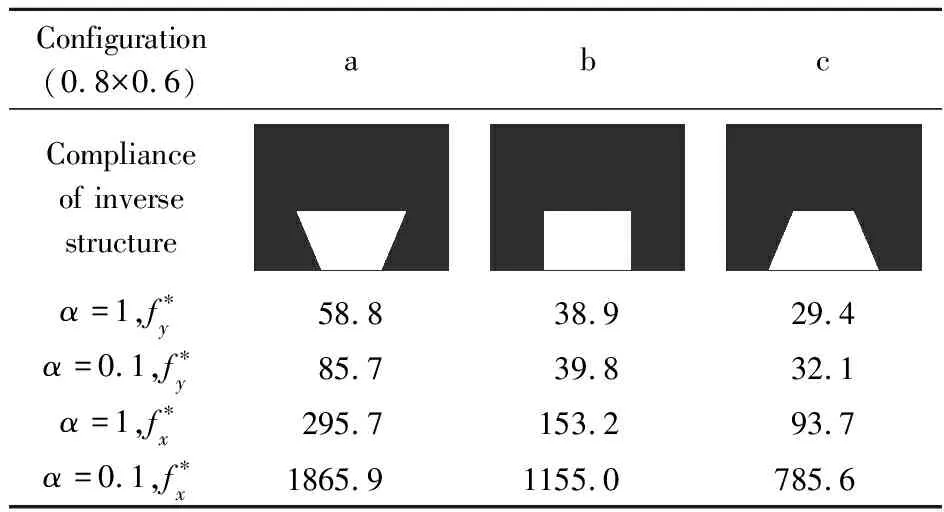
Tab.2 Compliance of the inverse structures with different loads and shear moduli

4.1.2 四角簡支板的優化

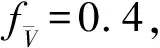
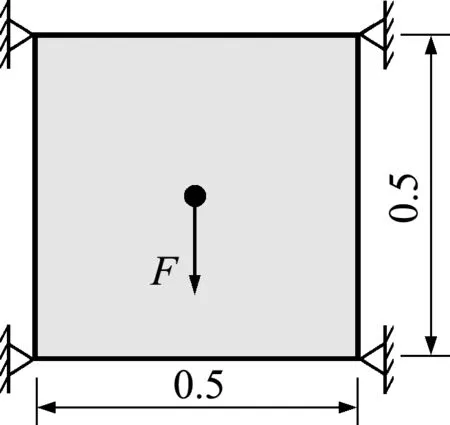
圖7 四角簡支板結構

分別給定上下左右四個方向和僅上下方向脫模的邊界條件，得到了圖8兩個優化結果，都符合給定的脫模條件。

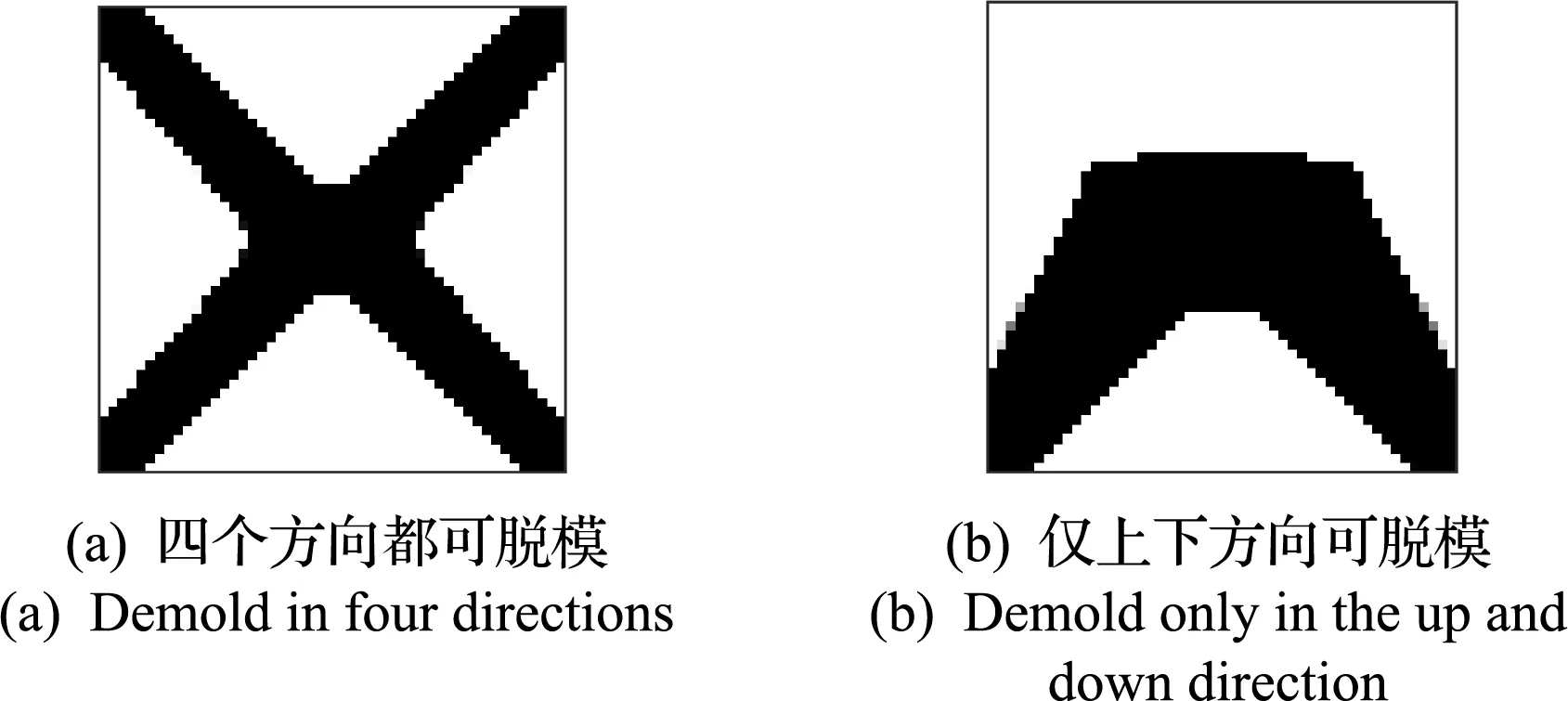
圖8 不同脫模條件的優化結果

4.2 三維結構算例

本文在Comsol 5.6實現了三維算例的優化。圖9給出了某四點簡支三維結構，上表面中心點受集中載荷F=1，結構離散為500個邊長為0.4的正六面體常應變單元。

圖9 三維結構

在無鑄造約束時最小化結構的柔順性，得到 圖10 的優化結果，從沿x方向的截面圖10(c)以及側視圖10(b)可以看出，在結構的中心部分存在不完全封閉的孔洞，不滿足可分型條件。

圖10 無鑄造約束的優化結果

采用本文方法，分別設置只能向上脫模和上下方向皆可脫模的邊界條件，分別得到圖11和圖12的優化解。這兩個優化結構沒有內孔和脫模方向上的側凹，因此滿足可鑄造約束。

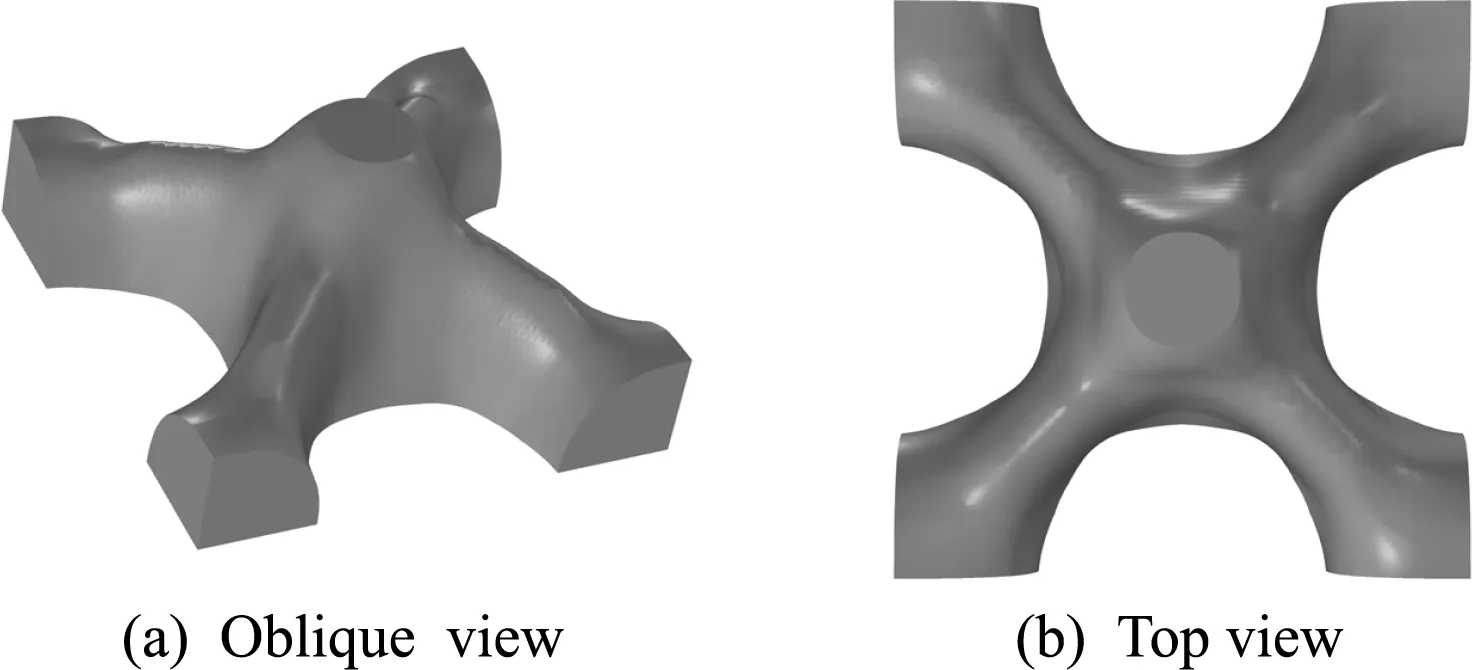
圖11 向上脫模的優化鑄件結構(顯示密度閾值為0.7)

圖12 上下方向皆可脫模的優化鑄件結構(顯示密度閾值為0.7)

5 結 論

本文提出了一種基于逆結構概念和附加重力場的鑄造約束方法。該方法對優化解的逆結構(可以看作是模具)施加重力，僅引入單個約束限制逆結構的最大柔順性，即可實現對優化解中內孔和側凹特征的抑制。二維和三維算例驗證了方法的有效性。該約束作為一個獨立約束，還適用于多種目標性能的結構拓撲優化問題。

與已有的虛擬標量場鑄造約束方法相比，本文方法不是對設計域內響應的最大值進行約束，而是對積分型表達式(逆結構的柔順性)進行約束。因此，該方法有利于優化求解過程的穩定收斂。

實際工程的鑄件優化設計問題更為復雜。一方面，除了鑄件本身，模具、型芯和澆鑄凝固系統的設計也需要優化；另一方面，鑄造工藝在持續發展，如結合3D打印技術的砂模鑄造(3DSP[24])降低了對鑄件的工藝約束要求，引入型芯也能提高鑄件的復雜度。這些都為拓撲優化真正與鑄造這一傳統工藝緊密結合提出了新的問題。將本文方法拓展用于復雜鑄件分型面和分型方向的優化，將是一個有意義的研究方向。

參考文獻(References):

[1] Cheng K T,Olhoff N.An investigation concerning optimal design of solid elastic plates [J].Interna-tionalJournalofSolidsandStructures,1981,17(3):305-323.

[2] 邊炳傳,隋允康.多約束作用下連續體結構的拓撲優化 [J].計算力學學報,2010,27(5):781-788.(BIAN Bing-chuan,SUI Yun-kang.Topology optimization of continuum structures under multiple constraints[J].ChineseJournalofComputationalMechanics,2010,27(5):781-788.(in Chinese))

[3] 陳 峰,陳飆松,周大為,等.結構拓撲優化中變量連接算法研究與軟件實現 [J].計算力學學報,2016,33(2):158-164.(CHEN Feng,CHEN Biao -song,ZHOU Da-wei,et al.Research and software implementation of variable connection algorithm for structural topo -logy optimization[J].ChineseJournalofComputationalMechanics,2016,33(2):158-164.(in Chinese))

[4] Li Q H,Chen W J,Liu S T,et al.Topology optimization design of cast parts based on virtual temperature method [J].CADComputer-AidedDesign,2018,94:28-40.

[5] Shyy Y K,Thomas H L.Topology Optimization with Manufacturing Constraints[A].World Congress of Structural & Multidisciplinary Optimization[C].2001.

[6] Harzheim L,Graf G.A review of optimization of cast parts using topology optimization [J].StructuralandMultidisciplinaryOptimization,2006,31(5):388-399.

[7] Lu J N,Chen Y H.Manufacturable mechanical part design with constrained topology optimization [J].Procee-dingsoftheInstitutionofMechanicalEngineers,PartB:JournalofEngineeringManufacture,2012,226(10):1727-1735.

[8] Xu B,Han Y S,Zhao L,et al.Topology optimization of continuum structures for natural frequencies considering casting constraints [J].EngineeringOptimization,2019,51(6):941-960.

[9] Gersborg A R,Andreasen C S.An explicit paramete -rization for casting constraints in gradient driven topology optimization [J].StructuralandMultidisciplinaryOptimization,2011,44(6):875-881.

[10] Guest J K,Zhu M.Casting and milling restrictions in topology optimization via projection-based algorithms [A].Proceedings of ASME 2012 International Design Engineering Technical Conference and Computers and Information in Engineering Conference [C].2012.

[11] Vatanabe S L,Lippi T N,de Lima C R,et al.Topo -logy optimization with manufacturing constraints:A unified projection-based approach [J].AdvancesinEngineeringSoftware,2016,100:97-112.

[12] Xia Q,Shi T L,Wang M Y,et al.A level set based method for the optimization of cast part [J].StructuralandMultidisciplinaryOptimization,2010,41(5):735-747.

[13] Xia Q,Shi T L,Yu W M,et al.Simultaneous optimization of cast part and parting direction using level set method [J].StructuralandMultidisciplinaryOptimization,2011,44(6):751-759.

[14] Allaire G,Jouve F,Michailidis G.Casting Constraints in structural optimization via a level-set method [A].10t hWorld Congress on Structural and Multidisciplinary Optimization[C].2013.

[15] Wang Y G,Kang Z.Structural shape and topology optimization of cast parts using level set method [J].InternationalJournalforNumericalMethodsinEngineering,2017,111(13):1252-1273.

[16] Qian X P.Undercut and overhang angle control in topology optimization:A density gradient based integral approach [J].InternationalJournalforNumericalMethodsinEngineering,2017,111(3):247-272.

[17] Liu S T,Li Q H,Chen W J,et al.An identification method for enclosed voids restriction in manufacturability design for additive manufacturing structures [J].FrontiersofMechanicalEngineering,2015,10(2):126-137.

[18] Wang C,Xu B,Meng Q X,et al.Topology optimization of cast parts considering parting surface position [J].AdvancesinEngineeringSoftware,2020,149:102886.

[19] Andreassen E,Clausen A,Schevenels M,et al.Efficient topology optimization in MATLAB using 88 lines of code [J].StructuralandMultidisciplinaryOptimization,2011,43(1):1-16.

[20] Stolpe M,Svanberg K.An alternative interpolation scheme for minimum compliance topology optimization [J].StructuralandMultidisciplinaryOptimization,2001,22(2):116-124.

[21] Xu S L,Cai Y W,Cheng G D.Volume preserving nonlinear density filter based on Heaviside functions [J].StructuralandMultidisciplinaryOptimization,2010,41(4):495-505.

[22] Svanberg K.MMAandGCMMATwoMethodsforNonlinearOptimization[M].2007.

[23] Wang F W,Lazarov B S,Sigmund O.On projection methods,convergence and robust formulations in topology optimization [J].StructuralandMultidisciplinaryOptimization,2011,43(6):767-784.

[24] Wang J Y,Sama S R,Manogharan G.Re -thinking design methodology for castings:3D sand-printing and topology optimization [J].InternationalJournalofMetalcasting,2019,13(1):2-17.