薄壁結構多層級并發加筋拓撲優化研究

(1.大連理工大學 工業裝備結構分析國家重點實驗室，大連 116024；2.大連銘云科技有限公司，大連 116023)

1 引 言

航天裝備大量采用網格加筋和周期性點陣等復雜薄壁結構，其重量占裝備結構干重的60%以上，輕量化需求十分迫切[1]。尤其面向以空天飛行器為代表的新一代航天裝備，其承力薄壁在大型化和精細化設計的發展趨勢下，往往還面臨高剛度和高抗屈曲等極端承載需求，給輕量化設計造成極大挑戰[2]。繼續基于傳統正置正交或三角形等單一規則加筋形式開展薄壁設計，已難以滿足結構的輕質高承載需求，只能通過犧牲結構的力學性能來實現輕量化設計。因此，亟需發展創新結構形式，并建立相應的結構設計方法，充分挖掘結構承載潛力，為新一代航天裝備的高性能承力薄壁提供支撐。

多層級結構是一類自然界常見的材料結構形式，其層級化的材料結構特點表現出高剛度、抗屈曲和抗缺陷等各種優異的力學性能[3]。這種通過豐富材料的結構層次來增強其力學性能的方法，為航天承力薄殼的創新結構設計提供了新的設計 思路。

受上述自然材料的啟發，本文針對航天裝備承力薄殼的高剛度和高抗失穩設計需求，提出了一種薄壁結構的多層級并發加筋拓撲優化方法，可同時給出主層級筋條布局形式和次層級點陣單胞構型，構成層級化的薄壁加筋結構形式。通過不同層級的加筋設計來滿足如整體承載和局部抗屈曲等不同層次的承載需求，有效擴展了結構設計空間，發掘利用結構承載潛力，獲得高承載的薄壁結構創新構型。

2 國內外現狀

早期的薄壁結構加筋設計主要采用均勻周期性網格加筋，如正置正交加筋和等三角加筋等，由于其結構形式相對簡單，可以通過全局啟發式參數優化和梯度參數優化的兩步驟流程獲得一組較優異的設計參數[4]，然而，簡單的結構形式難以應對復雜且嚴苛的承載環境，采用復雜的預設結構形式進行層級化結構的參數優化，其增加的參數變量又導致分析和優化迭代計算量呈幾何式增長[5]。為解決該問題，代表性工作包括深度學習方法[6]，通過卷積神經網絡提取加筋布局特征，從而提升優化迭代效率；近似求解方法[7]，解析地求解特定多層級加筋的失穩系數，從而縮短單次計算時間等。多層級加筋的參數優化研究表明，多層級加筋構型表現出改善結構整體剛度、局部穩定性和可靠性等多方面優點[8]。

然而，參數優化設計方法受制于設計人員預先給出的構型，難以改變加筋構型拓撲，對加筋布局設計域限制較大[9]。相對的，利用拓撲優化方法獲取概念設計能極大挖掘結構的承載能力。在薄壁加筋領域，隨著拓撲優化理論的發展，學者研究了基結構法[10]、沖壓約束[11,12]和B樣條參數描述[13]等數值處理技術，成功應用于變密度法、水平集法和剛度擴散法等拓撲優化方法中，突破了早期經典拓撲優化方法低體分比和灰度單元等數值求解問題[14]，實現了利用拓撲優化直接生成加筋特征，并在平面問題和中小規模的三維空間問題上取得了較好的成果。而針對包括航天裝備在內的大規模模型問題，上述方法由于高自由度帶來的計算效率問題和復雜承載帶來的優化收斂問題，難以得到實際工程應用[15]。為解決該問題，有研究基于大型航天薄壁其加筋點陣尺寸遠小于整體結構的幾何特點，對單胞進行了無限周期性的近似，實現了基于周期性邊界條件的等效數值方法，將周期性微結構轉化為等效屬性，其中代表性的方法有代表體元法[16]和漸進均勻化方法[17]。代表體元法在單胞邊界施加單位邊界條件，使代表性胞元與某種均勻結構的應變能相等，然后求解該均勻結構的材料屬性，力學意義直觀；漸進均勻化方法則通過單位特征應變進行漸進攝動展開，具有更嚴謹的數學基礎。利用上述方法，將結構設計轉換為材料設計，再根據單胞等效性能與結構形式的關系，就實現了單胞結構的逆均勻化設計，并成功應用于大規模筒殼結構的穩定性設計，有效提升了對薄壁結構的可設計性[18]。

圖1 多層級加筋設計

圖2 漸進均勻化雙尺度加筋單胞設計[18]

homogenization

面向新一代的結構設計需求，為實現進一步豐富結構形式，拓寬結構設計域，有學者提出多尺度設計方法[19]，將整體結構優化稱為宏觀設計，并在其中增加一組單元內的設計變量以表征材料屬性，稱為微觀設計，實現用一種弱材料替代實心材料，或先獲取多種材料屬性的整體布局，再通過逆均勻化設計對材料屬性進行解釋[20]，實現了格柵點陣的構型-布局并發設計[21]。該思路的代表工作是基于多孔各向異性材料法PAMP(Porous Anisotropic Material with Penalty)[22]的涂層-點陣填充優化[23]，利用逆均勻化方法并發獲得了平面問題下的涂層點陣設計。面向三維問題的差異化構型設計，有學者提出了實體-格柵并發優化設計[24]，通過一個兩步驟的優化進程，實現了典型航天設備的加筋-微桁架布局設計，較傳統單層級結構有極大性能提升。研究表明，層級化的設計思想可以提供優越的結構設計潛力，但仍表現出較多限制。現有設計方法或處理平面或小規模問題，而受限于優化計算成本，對高自由度的空間問題適用性差；或以單元尺度表述微結構，導致優化結果約束于單元內，優化構型在微結構的設計變量尺度內變化，層級設計不顯著；或使整體布局和微結構分別設計，人為干預性強。

圖3 多尺度并發設計方法

基于上述討論，為實現一種適用于大規模模型的多層級并發加筋設計，需要解決現有研究難以進行主次層級加筋構型清晰表征并優化的問題，突破空間問題下的多層級并發優化技術，進而實現薄壁結構多層級加筋結構優化設計。為此，本文發展了一種薄壁結構多層級并發加筋拓撲優化方法，可同時獲得優化的主層級稀疏加筋布局和次層級周期性點陣構型，有效擴展了薄壁結構加筋設計的初始設計域。通過層級化的筋條構型針對性承載不同類型的載荷，有利于提升薄壁結構在復雜載荷下的結構承載效率，為工程薄壁結構的輕質高承載設計提供了更先進的結構優化手段。

3 多層級并發拓撲優化方法

為實現層級化的主層級加筋與次層級點陣的并發優化，需要對兩種結構形式的構型進行統一描述，建立兩者間的等效剛度傳遞關系，并在每一次迭代中同步開展兩個層級的優化設計。本文提出的多層級并發加筋拓撲優化方法實施流程如圖4所示。首先，同時構建主層級筋條和次層級點陣的有限元數值模型，并根據設計需求初始化兩個層級的過濾和映射矩陣形式；然后，初始化或更新不同層級的設計變量，對于次層級點陣層次，計算其等效模量，并傳遞至主層級優化進程中，對于主層級模型，利用剛度和密度插值構建整體有限元分析模型；最后，計算獲得響應函數，同步獲得響應函數對各層次設計變量的靈敏度，并將上述主次層級分析數據代入優化求解器進行求解。重復上述優化過程直至滿足收斂條件，最終獲得優化的多層級加筋薄壁結構。

圖4 多層級并發拓撲優化流程

上述步驟的關鍵在于，需要建立主次層級間的等效剛度傳遞關系，以實現兩者的并發優化設計。還需要對周期性次層級結構進行等效表征，避免大規模的次層級分析導致優化迭代耗時無法接受。此外，需要對主次層級設計域施加筋條幾何約束，使優化結果呈現為清晰的加筋形式。

3.1 多層級并發拓撲優化模型

多層級并發拓撲優化框架對主層級稀疏加筋和次層級點陣構型進行同時設計并優化迭代。其中，次層級模型通過3.2節所述方法進行構建，主層級模型包含主層級加筋和次層級模型等效獲得的等效材料，兩者通過插值決定最終的剛度和密度。基于該思想，優化列式表示如下：

s.t.h(ρ,x)≤0

vm(ρ,x)≤0

ρ∈ρa d,x∈xa d

(1)

式中ρ為插值前的主層級有限元模型單元的偽密度，x為次層級點陣有限元模型單元的偽密度或幾何模型的控制參數，在3.2節進行具體說明，ρ和x分別為主層級加筋和次層級點陣的設計變量，ρa d和xa d為其可行域。f為目標函數，h為約束函數，vm為體分比約束。DM為主層級加筋和次層級點陣插值獲得的等效剛度，插值函數有多種表達形式，本文采用如下的剛度插值函數[25]，

(2)

(3)

多層級并發優化的程序實現流程總結如下。

Initialization： 建立多層級有限元分析模型，構建次層級點陣等效模型，初始化模型參數和優化參數，定義過濾矩陣(在3.3節說明)。

(1) 采用漸近均勻化方法求解次層級單胞的等效剛度屬性，計算等效剛度對次層級設計變量的導數(在3.2節說明)。

(2) 插值更新整體有限元模型，分析獲得目標函數、約束函數值及其對主層級加筋設計變量和次層級點陣等效材料屬性的導數。

(3) 通過鏈式法則分別求解對所有設計變量的敏度。

(4) 求解優化問題，更新設計變量，如果滿足收斂準則則結束優化，不滿足則返回步驟(1)。

3.2 次層級點陣單胞數值計算模型

為保證多層級并發優化的可行性和設計可用性，采用合理的等效手段將周期性點陣進行簡化極為重要。本文采用一種漸進均勻化方法的新求解方法[17]對次層級點陣進行等效，該方法通過將均勻化計算的單位應變場改為等效的位移場，使均勻化計算格式更為簡便，簡要介紹如下。

首先，采用特征位移表達特征應變，

(4)

(5)

根據單位應變，獲得節點反力為

(6)

(7)

式中Ks p為附加周期性邊界條件的的單胞總剛度陣。進而獲得等效剛度的有限元表達式為

(8)

基于上述方法，就實現了單胞模型的材料等效。如果采用殼單元進行計算，則采用板殼的周期性漸進均勻化方法[17]。本文后續算例均采用實體單元，故不詳細說明。

利用等效方法優化單胞構型，根據容許的計算時間、實際工程建模制造可行性等設計需求，本文給出兩種單胞結構的設計方法。第一種方法是單胞概念構型拓撲優化設計。該方法直接建立完整的單胞有限元模型，次層級點陣的設計變量為次層級單胞有限元模型單元的偽密度，優化迭代獲得拓撲優化生成的單胞構型。等效材料屬性對設計變量的敏度為

(9)

第二種方法是典型單胞構型設計，通過構建參數化的單胞幾何模型并進行有限元離散，獲取等效材料屬性，次層級點陣的設計變量為幾何模型的控制參數。利用該方法，可以直接使次層級點陣表現為一些工程中常見的構型(如三角形和六邊形)。為獲得參數化構型等效剛度對設計變量的敏度，如果采用差分法，則需要在每次優化迭代中進行多次計算，計算成本遠超出可接受范圍。構建數值插值模型能夠有效在優化迭代之前一次性完成所有計算，從而在后續迭代步驟中極大幅度縮小該步驟的計算時間[27]。基于上述問題，本文提出一種基于徑向基插值函數RBF(Radial Basis Function)[28]的次層級單胞快速等效流程。徑向基模型的表達式為

(10)

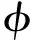
(11)

(12)

式中c為基函數的控制參數。目標函數對變量的敏度可以根據表達式顯式地計算。改變模型參數建立多個有限元模型，獲得等效剛度中的所有獨立變量，就可以構建多個獨立變量對參數的徑向基函數，并采用擬合精度評判標準對代理模型的精度進行評判，對于樣本量較小的模型，常用的評判標準有R2，Adj-R2和均方根誤差等[28]。對于部分工程構型，也可以參考其等效剛度解析表達式的研究[29]。為保證單胞的幾何特征，在選取周期性結構的單胞形狀時需要盡量選擇其代表胞元，并且控制單胞尺寸，使其周期陣列與宏觀整體結構的設計域相匹配。由于漸進均勻化計算的周期性邊界條件施加在單胞上，對單胞單元的數值處理均需要施加周期性條件。

3.3 優化的數值處理方法

變密度法拓撲優化需要通過過濾和映射方法處理棋盤格、灰度單元和網格依賴性等數值問題，薄壁結構的多層級并發拓撲優化方法還需要處理薄壁結構的多層級加筋表征問題。

基于偏微分方程的Helmholtz過濾方法由于不依賴單元臨域搜索，在大規模模型上表現出較大優勢[29]，并可以通過修改其過濾半徑，僅通過單元法向就可以實現大部分結構的加筋特征約束表征[11]。有限元離散的Helmholtz方程可表示為

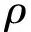
(13)

(14)

式中N為形函數，c為表示擴散效果的3×3二階正定張量，

(15)

式中V為單元空間向量的正交基，其中vn為加筋方向，根據數學描述或單元坐標法向量獲得，R為過濾半徑，rn設置為一個足夠大的值(遠大于厚度方向)，使過濾后vn方向的密度分布保持水平，在密度過濾時同時實現加筋特征的約束。

對于結構化網格，其單元編號規律簡單可循，可以直接設置變量連接以實現加筋特征約束，該線性映射表示為

ρe=Lρd

(16)

式中ρe為次層級單胞的偽密度，ρd為設置了變量連接后優化問題的實際設計變量，L為映射矩陣，該矩陣的構建方法為其第i列的第j行為1，使第j個單元的密度等于第i個單元的密度。

為解決灰度單元的問題，本文采用Heaviside密度映射[30],

(17)

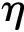
運用上述數值處理方法，任意響應函數對設計變量的靈敏度需要按照鏈式法則進行修正。

4 算例分析

4.1 四角簡支的方板最小化柔順度優化

以方形板為例，說明本方法在復合載荷條件下的剛度最大化問題。方板板長a=1000 mm，板厚為t=20 mm，主層級加筋筋高為hm=280 mm，次層級點陣高度為hs=130 mm。材料選用鋁，彈性模量E=71000 MPa，泊松比ν=0.3。底面的四個頂點沿三個方向固定，使板處于簡支狀態，施加兩個載荷，載荷N1=10000 N為板中心垂直朝向面外的集中力，載荷N2=1000 N為面內對邊雙向垂直的均布壓力。模型采用100×100×12的8節點六面體單元進行離散，其中板厚劃分3層單元，為不可設計域，主層級加筋設計域包含8層單元，次層級點陣包含設計域的下4層單元。主層級加筋沿板厚度方向設置變量連接。此外，作為一種合理的工程實踐，優化結構設置沿板邊垂直平分線對稱的變量連接約束，因此，主層級設計變量個數為100×100÷4=2500。結構整體的體積約束設為15%。

圖5 四邊簡支方板模型

本算例優化列式采用方程(1)，其中，目標函數f為結構柔順度C，其可表示為

(18)

式中DM為主層級加筋和次層級點陣插值獲得的等效剛度，由設計變量ρ和x決定，Kk為整體模型單元剛度陣，uk為有限元求解的單元位移。多層級并發拓撲優化的靈敏度推導分為兩部分，對主層級加筋設計變量的導數和對次層級點陣設計變量的導數。對于本問題，目標函數對主層級加筋的靈敏度推導與傳統拓撲優化方法類似，基于伴隨法，可表示為

(19)

式中g′(ρ)為材料插值函數對宏觀設計變量的敏度，對于本文選取的插值函數，g′(ρ=pαρ(p -1)-α。在實際處理中，可以首先計算剛度相同單元的應變能，然后再將g′(ρ)作為系數相乘以減少重復計算。

目標函數對次層級點陣等效材料的敏度為

(20)

由于等效剛度系數含21個獨立變量，因此對每個單元需要計算21次，為提升計算效率，可以按照同樣的方法減少重復計算，并由于單元層級內每個計算之間沒有耦合效應，可以采用并行計算技術加快求解效率。獲取目標函數對次層級點陣單胞材料系數的靈敏度后，再根據3.2節方法，根據鏈式法則就可以求得目標函數對微觀設計變量的敏度。約束函數h為最大尺寸約束，通過控制半徑內的總材料密度，使優化結果呈現為加筋形式，本文采用如下的表達形式[31]，

(21)

式中pn為p范數參數，γ為局部尺寸約束上限。

為完整展示多層級加筋優化方法，并與傳統單層級加筋優化方法進行對比，本節共開展三個優化，優化1為傳統單層級優化，優化2為基于典型單胞構型設計的多層級并發優化，優化3為單胞概念構型拓撲優化設計的多層級并發優化。在實際處理上，三個優化問題的區別表現為其次層級模型處理上的不同,優化1等價于多層級并發優化中直接令次層級剛度為0。優化2采用正置正交的加筋形式，并利用3.2節所述方法進行等效。為準確描述材料的性能，提供大量不同尺寸的模型進行擬合，由于參數化建模和有限元分析的處理不進入優化迭代循環，因此對整體計算時間沒有顯著影響。優化3構建次層級單胞網格為100×100×10，并沿厚度方向設置變量連接，因此次層級設計變量為100×100=10000個。

優化結果如圖6所示。為更清晰地表示優化結果，通過后處理將次層級點陣構型完整展示在整體模型上。圖6的三個優化結果的柔順度依次為2564.8 J，2363.7 J和2355.3 J。典型構型次層級點陣的多層級并發拓撲優化結果中，主層級加筋與次層級點陣的材料體積比例為VM∶VS=70.9%∶29.1%，拓撲構型次層級點陣的多層級并發拓撲優化結果中，主層級加筋與次層級點陣的材料體積比例為VM∶VS=70.8%∶29.2%。

圖6 方板拓撲優化結果

將優化結果總結如圖7所示，可以看出，多層級并發優化獲得了主層級稀疏加筋和次層級點陣的層級化結構形式，與單層級加筋優化的結構形式區別顯著。多層級并發優化剛度較單層級優化剛度有較大提升，兩個多層級優化結果(圖6(b,c))相對于單層級優化結果(圖6(a))，柔順度分別減小了7.8%和8.2%。該結果表明，通過多層級并發拓撲優化方法，獲得的多層級加筋構型承載能力優于單層級加筋構型。

圖7 算例1的優化結果對比

為進一步討論載荷邊界對優化結果的影響，修改本算例的載荷大小，分別令N1或N2=0，開展兩個新的優化算例。優化結果如圖8所示。可以看出，對于僅存在面外集中力N1的載荷工況，最終的優化結果僅包含主層級稀疏加筋，呈現為斜十字形加筋形式，而次層級點陣體積約為0，這一結果與該問題的一般解[9,10,32]相同；而對于只有對邊壓力N2的載荷工況，其結果僅包含次層級點陣構型，主層級筋條體積約為0，呈現為非均勻的正置正交構型。

圖8 修改承載條件下的多層級優化結果

上述結果表明，盡管多層級加筋結構形式拓展了薄壁結構的初始設計空間，但優化結果的層級化程度與載荷邊界具有強相關性，單一載荷邊界下的優化結果可能不呈現為多層級構型。具體而言，對于單一的集中載荷邊界，優化結果往往呈現為稀疏的主層級加筋形式，且主層級筋條布局接近當前工況下的最優傳力路徑，從而實現結構整體柔順度最小化；對于單一的均布載荷邊界，優化結果往往呈現為密集的周期性加筋構型，均勻化地增強結構整體，從而抵抗均勻的載荷；對于兼具集中載荷與均布載荷的復雜載荷邊界，此時優化結果呈現為多層級加筋構型，通過主層級筋條抵抗集中載荷，通過次層級筋條抵抗均布載荷，從而獲得更高承載性能的優化結果。

4.2 穩定性約束下的加筋曲殼最小柔順度優化

本節以曲殼為例，展示本方法在剛度和穩定性的雙重設計需求下的優化效果。加筋曲殼幾何模型如圖9所示，為一個1/6圓柱殼，其直邊長d=500 mm，外徑r=250 mm，殼厚t=2 mm，筋高h=8 mm，次層級點陣的高度為主層級筋條的一半，材料選用鋼，彈性模量E=210000 MPa，泊松比ν=0.37。曲殼兩端約束垂直于曲殼方向的兩個自由度，并施加朝向曲殼內的均勻軸壓N=800 N。

圖9 曲殼模型

模型劃分為48384個六面體單元，其中殼厚為3層單元。加筋約束采用3.3節所述的各向異性過濾方法生成加筋，設置加筋方向過濾半徑rn=1500。體分比約束為30%，主層級設計變量為48384個。優化目標為在保證結構一階線性臨界失穩系數大于1的前提下最小化結構柔順度。對于該問題，注意需要對次層級等效材料的主方向進行設置，彈性矩陣的轉換矩陣表達式為

(22)

本算例的優化列式采用方程(1)，其中，目標函數f為結構柔順度C，其表達式和敏度推導與4.1節相同。約束函數h為結構一階線性臨界失穩載荷，其計算及其敏度計算推導如下。一般而言，求解結構失穩臨界承載力的特征值問題是求解其逆特征值為

(23)

式中Kσ M為初應力矩陣(幾何剛度陣)，KM為結構剛度陣，兩者均通過主層級加筋和次層級點陣剛度插值并組合。單元的初應力矩陣表示為

(24)

式中G為排序后的形函數微分項，S為結構應力矩陣，其表示為

(25)

(26)

KM的相關計算見4.1節。Kσ M對任意設計變量的導數為

(27)

為避免計算?u/?x，利用伴隨法計算如下,

(28)

式中伴隨向量v根據以下伴隨方程求解，

(29)

式中Kσ M的偏導數計算只需要計算其中結構應力矩陣S的偏導數，關于其分項s的計算表達式為

(30)

式中I為單位矩陣。對次層級單胞設計變量的敏度同樣利用鏈式法則計算獲得。

構建與4.1節相似的三個優化問題，其中，優化2選用正三角形單胞，優化3構建單胞模型劃分為80×80×20個單元，沿厚度方向設置變量連接，并設置對稱約束，變量數為80×80÷4=1600。

優化結果如圖10所示，圖10的三個優化結果的一階失穩系數依次為1.52，1.28和1.36，滿足穩定性約束，三者的柔順度依次為506.88 kJ，432.19 kJ和372.08 kJ。典型構型次層級點陣的多層級并發優化結果中，主層級加筋與次層級點陣的材料體積比例為VM∶VS=60.1%∶39.9%，拓撲構型次層級點陣的多層級并發優化結果中，主層級加筋與次層級點陣的材料體積比例為VM∶VS=66.5%∶33.5%。將優化結果總結如圖11所示，并展示了三個優化結構的一階失穩模態。結果顯示，兩個多層級優化結果(圖10(b，c))相對于單層級優化結果(圖10(a))，柔順度分別減小了14.7%和26.6%，多層級并發優化的剛度相對于單層級優化有顯著提升。

圖10 曲殼優化結果

圖11 算例2的優化結果對比

本節算例的多層級并發優化構型同樣呈現出與單層級加筋優化的明顯區別。在雙重設計目標的復雜約束下，單層級加筋結構為提升結構抗失穩能力，將部分材料布置于非直接傳力路徑，導致結構整體剛度下降，而多層級加筋構型通過主次層級筋條共同作用，在保證結構整體承載能力的同時，同步增強薄殼整體和局部抗彎剛度，改變結構失穩模態，提升結構抗屈曲能力。其次，上述算例中，在相同的屈曲約束下，拓撲點陣優化構型的結構承載力明顯優于預設的正三角點陣優化構型，前者的柔順度降低程度是后者的1.8倍。這說明，相比傳統單層級加筋和典型次層級點陣的多層級加筋設計，主層級筋條布局和次層級點陣構型的共同設計可給出更優的兼具剛度和抗屈曲承載能力的薄壁結構設計。

5 結 論

本文提出了一種薄壁結構的多層級并發加筋設計方法，在一次拓撲優化求解中同時生成主層級稀疏加筋和次層級密集點陣構型，擴展了結構優化設計空間，獲得創新結構形式，利用主次層級的筋條結構針對性地抵抗復雜載荷邊界，有效提升了材料利用率。優化算例表明，多層級并發加筋可以優化兩層級加筋的體積比例及兩層級加筋的拓撲布局，優化結構承載效率，在復雜邊界環境及設計指標下，主次層級加筋可以協同作用，有效提升結構承載能力。本方法提供的優化構型工程實用性強，能夠有效應用于航天裝備的薄壁結構優化，也可以延拓至常見薄壁結構主承力結構，從而有效提升裝備薄壁結構的承載效率。

參考文獻(References):

[1] 王 博，郝 鵬，田 闊.加筋薄殼結構分析與優化設計研究進展[J].計算力學學報,2019,36(1):1-12.(WANG Bo,HAO Peng,TIAN Kuo.Recent advances in structural analysis and optimization of stiffened shells [J].ChineseJournalofComputationalMe-chanics,2019,36(1):1-12.(in Chinese))

[2] 全棟梁,時光輝,關成啟,等.結構優化技術在高速飛行器上的應用與面臨的挑戰[J]:力學與實踐,2019,41(4):373-381,415:(QUAN Dong-liang,SHI Guang-hui,GUAN Cheng-qi,et al.Applications and challenges of structural optimization in high-speed aerocraft [J].MechanicsinEngineering,2019,41(4):373-381,415.(in Chinese))

[3] Fratzl P,Weinkamer R.Nature’s hierarchical materials[J].ProgressinMaterialsScience,2007,52(8):1263-1334.

[4] Bagheri M,Jafari A A,Sadeghifar M.A genetic algorithm optimization of ring-stiffened cylindrical shells for axial and radial buckling loads[J].ArchiveofAppliedMechanics,2011,81(11):1639-1649.

[5] 鄧亞權.基于代理模型的結構疲勞壽命優化方法、軟件及應用[D].南京航空航天大學,2010.(DENG Ya-quan.Method,Software and Application of Structural Fatigue Life Optimization Based on Metamodels[D].Nanjing University of Aeronautics and Astronautics,2010.(in Chinese))

[6] Hao P,Liu D C,Zhang K P,et al.Intelligent layout design of curvilinearly stiffened panels via deep lear-ning-based method[J].Materials&Design,2021,197:109180.

[7] 徐元銘，李松澤.整體次加筋壁板屈曲載荷近似計算方法[J].北京航空航天大學學報,2015,41(3):369-374.(XU Yuan-ming,LI Song-ze.Approximate calculation method of buckling load on integral sub-stiffened panel[J].JournalofBeijingUniversityofAeronauticsandAstronautics,2015,41(3):369-374.(in Chinese))

[8] Wang B,Tian K,Zhou C H,et al.Grid-pattern optimization framework of novel hierarchical stiffened shells allowing for imperfection sensitivity[J].AerospaceScienceandTechnology,2017,62:114-121.

[9] 鐘煥杰.薄壁加筋結構的拓撲優化方法研究[D].南京航空航天大學,2015.(ZHONG Huan-jie.Research on Topology Optimization of Stiffened Plates[D].Nanjing University of Aeronautics and Astronautics,2015.(in Chinese))

[10] 董小虎，丁曉紅.基于自適應成長法的周期性加筋結構拓撲優化設計方法[J].中國機械工程,2018,29(17):2045-2051.(DONG Xiao -hu,DING Xiao -hong.Topology optimum design method for periodic stiffe -ner structures based on adaptive growth method[J].ChinaMechanicalEngineering,2018,29(17):2045-2051.(in Chinese))

[11] Wang B,Zhou Y,Tian K,et al.Novel implementation of extrusion constraint in topology optimization by Helmholtz-type anisotropic filter[J].StructuralandMultidisciplinaryOptimization,2020,62(4):2091-2100.

[12] 張衛紅，章勝冬，高 彤.薄壁結構的加筋布局優化設計[J].航空學報,2009,30(11):2126-2131.(ZHANG Wei-hong,ZHANG Sheng-dong,GAO Tong.Stiffener layout optimization of thin walled structures[J].ActaAeronauticaetAstronauticaSinica,2009,30(11):2126-2131.(in Chinese))

[13] Feng S Q,Zhang W H,Meng L,et al.Stiffener layout optimization of shell structures with B -spline parame -terization method[J].StructuralandMultidisciplinaryOptimization,2021,63(6):2637-2651.

[14] Olhoff N,Bends?e M P,Rasmussen J.On CAD -integrated structural topology and design optimization[J].ComputerMethodsinAppliedMechanicsandEngineering,1991,89(1-3):259-279.

[15] Wagner H N R,Hühne C,Rohwer K,et al.Stimulating the realistic worst case buckling scenario of axially compressed unstiffened cylindrical composite shells[J].CompositeStructures,2017,160:1095-1104.

[16] Xia Z H,Zhang Y F,Ellyin F.A unified periodical boundary conditions for representative volume elements of composites and applications[J].InternationalJournalofSolidsandStructures,2003,40(8):1907-1921.

[17] 蔡園武.周期性板結構的漸近均勻化方法及微結構優化[D].大連理工大學,2014.(CAI Yuan-wu.Asymp -totic Homogenization of Periodic Plate and Micro -Structural Optimization[D].Dalian University of Technology,2014.(in Chinese))

[18] Zhou Y,Tian K,Xu S L,et al.Two -scale buckling topology optimization for grid-stiffened cylindrical shells[J].Thin-WalledStructures,2020,151:106725.

[19] Wu J,Sigmund O,Groen J P.Topology optimization of multi-scale structures:a review[J].StructuralandMultidisciplinaryOptimization,2021,63(3):1455-1480.

[20] Rodrigues H,Guedes J M,Bendsoe M P.Hierarchical optimization of material and structure[J].StructuralandMultidisciplinaryOptimization，2002,24(1):1-10.

[21] 易斯男.基于均勻化的周期性梁板結構降階及拓撲優化[D].大連理工大學,2015.(YI Si-nan.Model Reduction and Topology Optimization of Periodic Beam and Plate Structure Based on Homogenization[D].Dalian University of Technology,2015.(in Chinese))

[22] 劉 嶺，閻 軍，程耿東.考慮均一微結構的結構/材料兩級協同優化[J].計算力學學報，2008,25(1):29-34.(LIU Ling,YAN Jun,CHENG Geng-dong.Structure -material concurrent optimization considering uniform material microstructure[J].ChineseJournalofComputationalMechanics,2008,25(1):29-34.(in Chinese))

[23] Wadbro E,Niu B.Multiscale design for additive ma-nufactured structures with solid coating and periodic infill pattern[J].ComputerMethodsinAppliedMe-chanicsandEngineering，2019,357:112605.

[24] Wang C,Zhu J H,Wu M Q,et al.Multi-scale design and optimization for solid-lattice hybrid structures and their application to aerospace vehicle components[J].ChineseJournalofAeronautics，2021,34(5):386-398.

[25] Sigmund O.Design of multiphysics actuators using topology optimization.Part II:Two -material structures[J].ComputerMethodsinAppliedMechanicsandEngineering，2001,190(49-50):6605-6627.

[26] Zhu J H,Zhang W H,Beckers P.Integrated layout design of multi-component system[J].InternationalJournalforNumericalMethodsinEngineering，2009,78(6):631-651.

[27] Wang C,Gu X J,Zhu J H,et al.Concurrent design of hierarchical structures with three -dimensional para-meterized lattice microstructures for additive manufacturing[J].StructuralandMultidisciplinaryOptimization，2020,61(3):869-894.

[28] 艾依斯，張愛蓮，吳義忠.一種改進的RBF全局優化方法[J].計算機工程與應用，2012,48(15):43-48.(AI Yi-si,ZHANG Ai-lian,WU Yi-zhong.Improved global optimization method using radial basis functions[J].ComputerEngineeringandApplications,2012,48(15):43-48.(in Chinese))

[29] Lazarov B S,Sigmund O.Filters in topology optimization based on Helmholtz-type differential equations[J].InternationalJournalforNumericalMethodsinEngineering，2011,86(6):765-781.

[30] Guest J K,Prévost J H,Belytschko T.Achieving minimum length scale in topology optimization using nodal design variables and projection functions[J].InternationalJournalforNumericalMethodsinEngineering，2004,61(2):238-254.

[31] Guest J K.Imposing maximum length scale in topology optimization[J].StructuralandMultidisciplinaryOptimization，2009,37(5):463-473.

[32] 崔榮華.基于拓撲優化框架的薄板加強筋布局優化[D].大連理工大學,2019.(CUI Rong-hua.Layout Optimization of Stiffeners Based on Topology Optimization Framework[D].Dalian University of Techno -logy,2019.(in Chinese))