基于參數(shù)化水平集方法的微結(jié)構(gòu)拓撲優(yōu)化設(shè)計

魏 鵬,2， 范海堅， 李雪平*， 蘇 成

(1.華南理工大學(xué) 土木與交通學(xué)院，亞熱帶建筑科學(xué)國家重點實驗室，廣州 510640；2. 華南理工大學(xué) 廣東省高分子先進制造技術(shù)及裝備重點實驗室，廣州 510640)

1 引 言

材料在微觀尺度下可以看作是由眾多擁有相似拓撲的微結(jié)構(gòu)周期性排列而成的，且材料在宏觀尺度下的屬性不僅與材料本身的物理本質(zhì)屬性有關(guān)，還取決于材料內(nèi)部微結(jié)構(gòu)的拓撲[1]。為了獲得微結(jié)構(gòu)周期性排列的復(fù)合材料的性能，學(xué)者們通過均勻化方法來預(yù)測構(gòu)成復(fù)合材料的周期性微結(jié)構(gòu)的宏觀等效屬性[2]。通過逆向均勻化方法可以實現(xiàn)微結(jié)構(gòu)的拓撲優(yōu)化設(shè)計[3]，即以微結(jié)構(gòu)的宏觀等效屬性為目標，通過迭代更新微結(jié)構(gòu)內(nèi)材料的分布狀態(tài)，最終使材料在宏觀尺度上表現(xiàn)出滿足目標最優(yōu)的性質(zhì)。復(fù)合材料在物理性質(zhì)、機械性能和熱性能等方面具有單一材料不具備的優(yōu)勢，并在航空航天、汽車和機械等領(lǐng)域中得到了研究和應(yīng)用。目前已有眾多學(xué)者采用拓撲優(yōu)化方法設(shè)計了剛度和熱傳導(dǎo)性最大化[4]、磁導(dǎo)率最大化[5]、流體滲透性最大化[6]和具有負熱擴散系數(shù)[7]等性質(zhì)的材料。

拓撲優(yōu)化領(lǐng)域近幾十年來在以程耿東等[8]為代表的學(xué)者做出的奠基性工作下不斷發(fā)展進步。程耿東等[9]針對變厚度彈性薄板進行剛度優(yōu)化設(shè)計，為連續(xù)體拓撲優(yōu)化做出了先驅(qū)性工作。針對受到應(yīng)力約束的結(jié)構(gòu)拓撲優(yōu)化問題，提出ε放松算法解決了應(yīng)力奇異性問題。最近又提出了用序列整數(shù)規(guī)劃方法求解拓撲優(yōu)化問題[10]，為拓撲優(yōu)化領(lǐng)域的發(fā)展作出了重要貢獻。

本文拓撲優(yōu)化模型采用的水平集方法最早由Osher等[11]提出，用于描述曲線和曲面的演化過程，應(yīng)用于圖像處理和計算機視覺等界面追蹤領(lǐng)域。隨后Sethian等[12]將水平集方法引入到結(jié)構(gòu)拓撲優(yōu)化研究中。水平集方法通過隱式模型描述結(jié)構(gòu)演化邊界，具有能夠自動處理拓撲變化并獲得清晰光滑邊界的優(yōu)勢。傳統(tǒng)水平集方法通過求解H-J(Hamilton-Jacobi)方程推動水平集函數(shù)點水平運動實現(xiàn)邊界演化，這導(dǎo)致在求解過程中存在無法自動開孔和對初始設(shè)計依賴性高等問題。針對上述問題，學(xué)者們提出了半隱式格式的水平集方法[13]、分片常數(shù)水平集方法[14]、基于反應(yīng)擴散方程的水平集方法[15]和參數(shù)化水平集方法[16]等，這些方法在一定程度上克服了傳統(tǒng)水平集方法無法自動開孔的不足，但仍部分存在著數(shù)值不穩(wěn)定及對初始設(shè)計依賴性高的問題。

本文采用參數(shù)化水平集方法，更新了水平集函數(shù)迭代格式，實現(xiàn)了自動開孔；結(jié)合水平集帶方法，對零水平集附近的材料密度進行插值處理使其分布在[0,1]范圍內(nèi),設(shè)計邊界在優(yōu)化過程中引入了中間密度以提高優(yōu)化過程中的穩(wěn)定性。并將上述方法應(yīng)用于包括體積模量或剪切模量最大化和具有負泊松比性質(zhì)的材料拓撲優(yōu)化問題中，研究不同體積分數(shù)約束、多種初始設(shè)計及水平集帶方法對優(yōu)化結(jié)果的影響。

2 引入水平集帶的參數(shù)化水平集方法

2.1 傳統(tǒng)水平集方法

水平集方法核心思想是構(gòu)建一個高一維的水平集函數(shù)，通過該水平集函數(shù)曲面與零平面的交線來表達材料分布區(qū)域的邊界，如圖1所示。其邊界的定義可以表示為

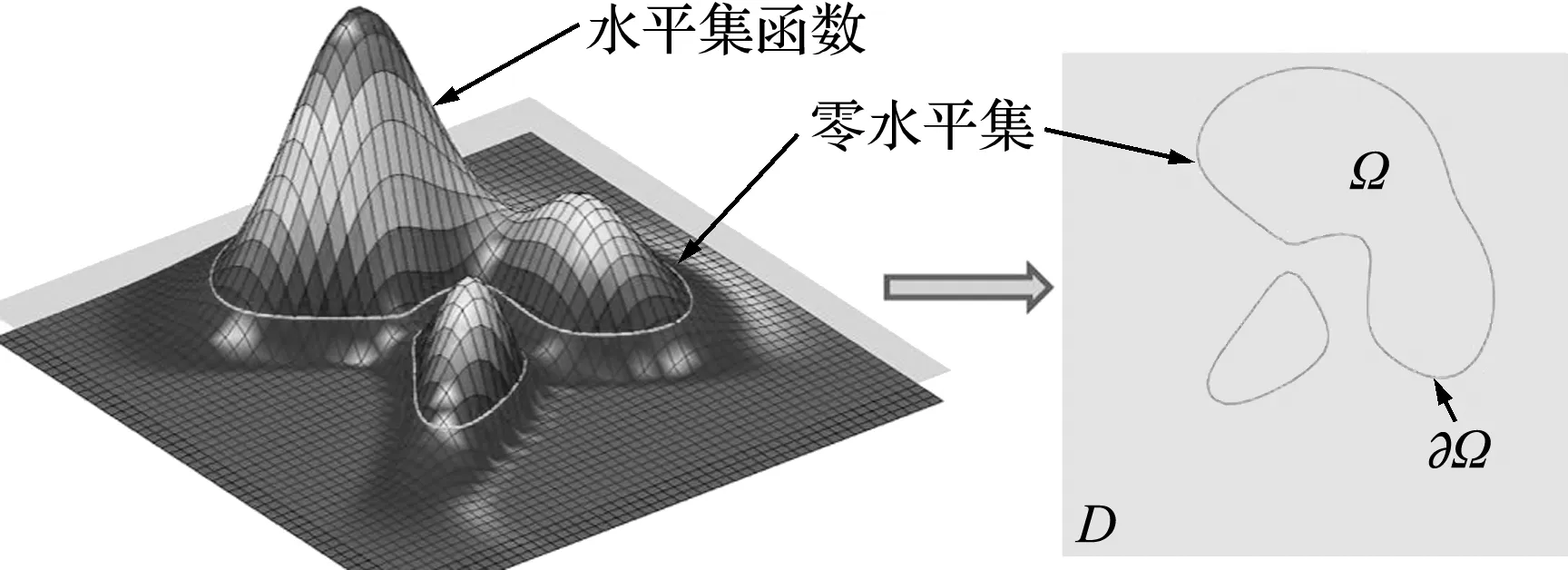
圖1 水平集函數(shù)(左)及對應(yīng)的材料分布區(qū)域的邊界(右)

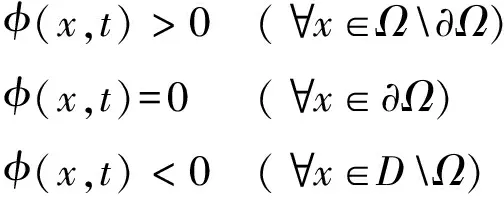
(1)

傳統(tǒng)水平集方法通過求解描述水平集函數(shù)演化方程，即下式的H-J偏微分方程來進行更新,

(2)

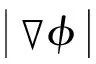
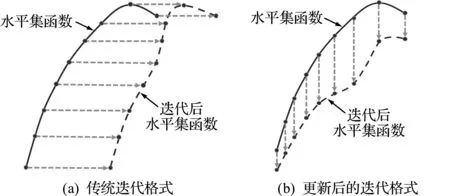
圖2 更新前后的迭代格式

2.2 轉(zhuǎn)換參數(shù)化水平集的迭代格式

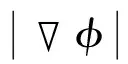
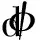
(3)

此時原來的H-J偏微分方程轉(zhuǎn)換為更易求解的常微分方程，水平集函數(shù)的更新也僅取決于邊界的法向速度Vn。如圖2(b)所示，水平集函數(shù)的更新轉(zhuǎn)換為各點的豎向運動，Vn的物理意義也變成了水平集函數(shù)點的豎向運動速度。

同時本文采用參數(shù)化水平集方法，引入基函數(shù)對水平集函數(shù)進行插值，將水平集函數(shù)轉(zhuǎn)化為一系列基函數(shù)和相應(yīng)參數(shù)的線性組合,

(4)

式中n為基函數(shù)數(shù)目，g(x)為基函數(shù)，α為對應(yīng)的展開系數(shù)。基函數(shù)的選取可以根據(jù)需要選擇為徑向基函數(shù)、B樣條函數(shù)和有限元形函數(shù)等[17]。本文采用MQ徑向基函數(shù)，其形式為

(5)

式中xi為第i個節(jié)點的坐標，c為很小的常數(shù)。基函數(shù)僅與空間坐標相關(guān)，通過更新相應(yīng)的參數(shù)α即可實現(xiàn)水平集函數(shù)的演化。由此可得到以α為設(shè)計變量的水平集函數(shù)迭代格式，

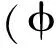
(6)

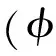
2.3 引入水平集帶方法

水平集方法會嚴格地將邊界兩側(cè)材料劃分為{0,1}分布，在邊界演化過程中會導(dǎo)致材料密度的突變，孔洞的生成消失都會造成數(shù)值的不穩(wěn)定。而變密度法由于引入了中間密度，故在迭代演化中能夠保持較好的連續(xù)性和穩(wěn)定性。為了將變密度法中間密度的拓撲表現(xiàn)潛力引入水平集方法中，Wei等[18]提出了水平集帶方法，故在零水平集附近的單元引入中間密度。即在原零水平集上下一定范圍內(nèi)引入密度插值函數(shù)，水平集帶內(nèi)的水平集函數(shù)值將會通過密度插值函數(shù)映射到指定的密度范圍，表達式為

(7)

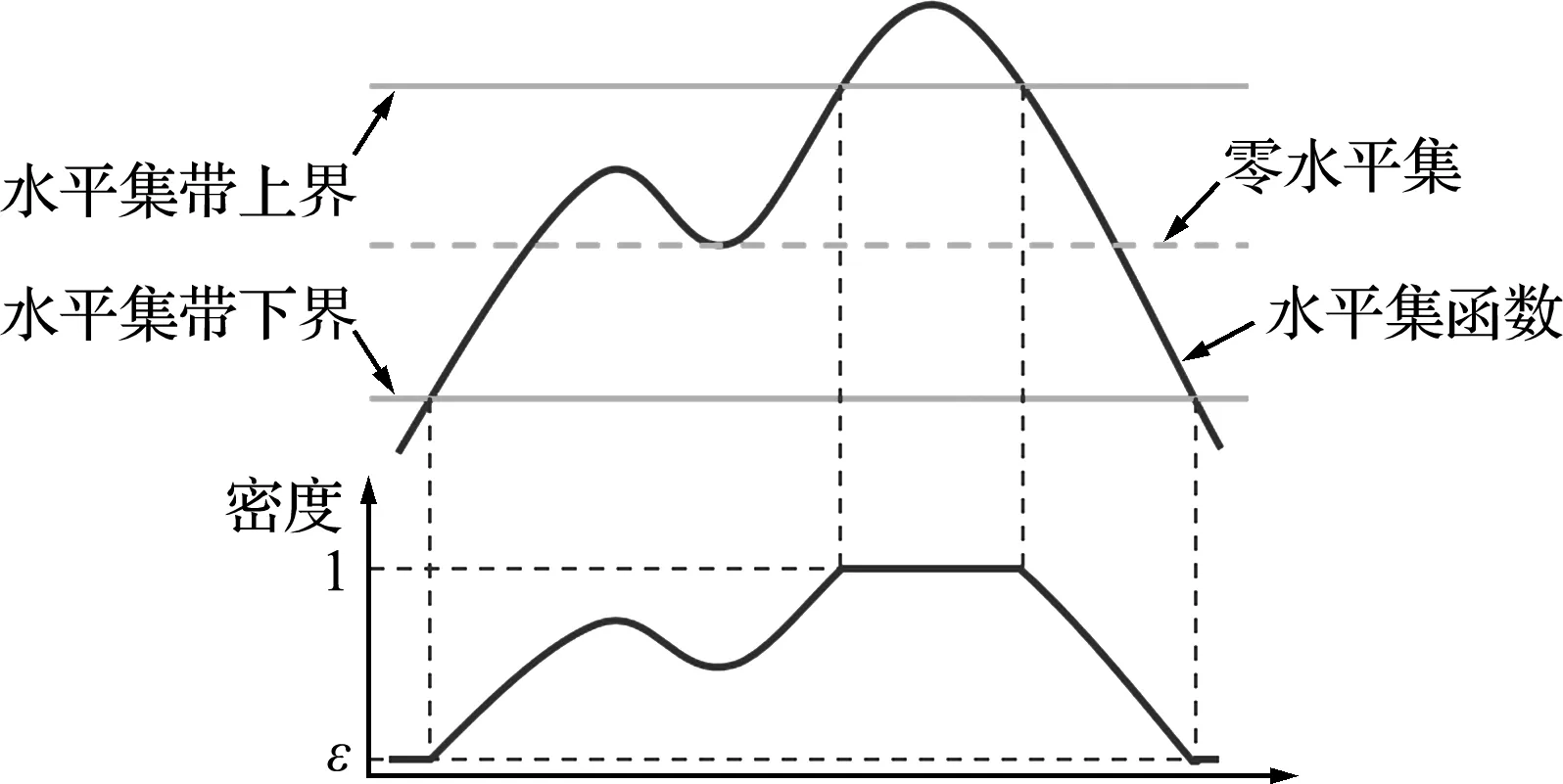
圖3 水平集帶方法

3 能量均勻化方法和拓撲優(yōu)化模型

3.1 能量均勻化方法

一個宏觀非均質(zhì)的結(jié)構(gòu)可以看作是由微觀尺度上微結(jié)構(gòu)單胞周期性重復(fù)組合構(gòu)成，通過均勻化方法可以研究微觀結(jié)構(gòu)在周期性重復(fù)排列后的等效力學(xué)性能。

假設(shè)x為結(jié)構(gòu)宏觀尺度的全局變量，y=x/ε為材料微觀尺度的局部變量，根據(jù)漸進展開理論，結(jié)構(gòu)的宏觀位移場uε(x,y)可以按參數(shù)ε展開為

uε(x,y)=ε0u0(x,y)+ε1u1(x,y)+

ε2u2(x,y)+…

(8)

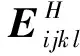
(9)

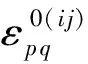
(10)

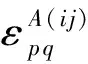
(11)

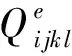
3.2 材料微結(jié)構(gòu)拓撲優(yōu)化設(shè)計模型

本文基于參數(shù)化水平集方法構(gòu)建材料微結(jié)構(gòu)的拓撲優(yōu)化模型，將微結(jié)構(gòu)的宏觀等效特性作為拓撲優(yōu)化的目標函數(shù)，

(12)

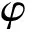
(13)

(14)

根據(jù)均勻化方法的等效彈性剛度矩陣定義，最大化材料體積模量的目標函數(shù)定義為

(15)

式中K為體積模量值。最大化材料剪切模量的目標函數(shù)定義為

(16)

式中G為剪切模量值。由于負泊松比材料的特殊性，以負泊松比為目標的材料設(shè)計更為復(fù)雜。根據(jù)泊松比的定義，泊松比的計算如下，

(17)

因此目標函數(shù)選取為剛度矩陣中各元素的組合[19]

(18)

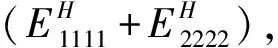
4 數(shù)值算例與結(jié)果分析

本節(jié)分別針對最大化體積模量、剪切模量和具有負泊松比的材料進行拓撲優(yōu)化設(shè)計。其中實體材料和空材料的楊氏模量分別為1和1×10-9，泊松比均為0.3，有限元網(wǎng)格劃分為50×50。

4.1 體積模量最大化

以體積模量最大化為目標函數(shù)，體積分數(shù)為0.5。水平集帶初始帶寬為3，每次迭代減小0.1，最終帶寬收斂至0。圖4是對應(yīng)的水平集函數(shù)及水平集帶。表1列出了不同迭代步下的微結(jié)構(gòu)拓撲及其密度分布。圖4在迭代開始時，零水平集上下存在著水平集帶邊界，邊界內(nèi)的水平集函數(shù)對應(yīng)的單元密度在ε和1之間，如圖1所示此時存在著許多中間密度單元。隨著優(yōu)化的進行，水平集帶上下邊界逐漸收縮至重合，中間密度單元逐漸消失，單元密度接近黑白分明的{ε,1}分布。

圖4 水平集函數(shù)及水平集帶的演化過程

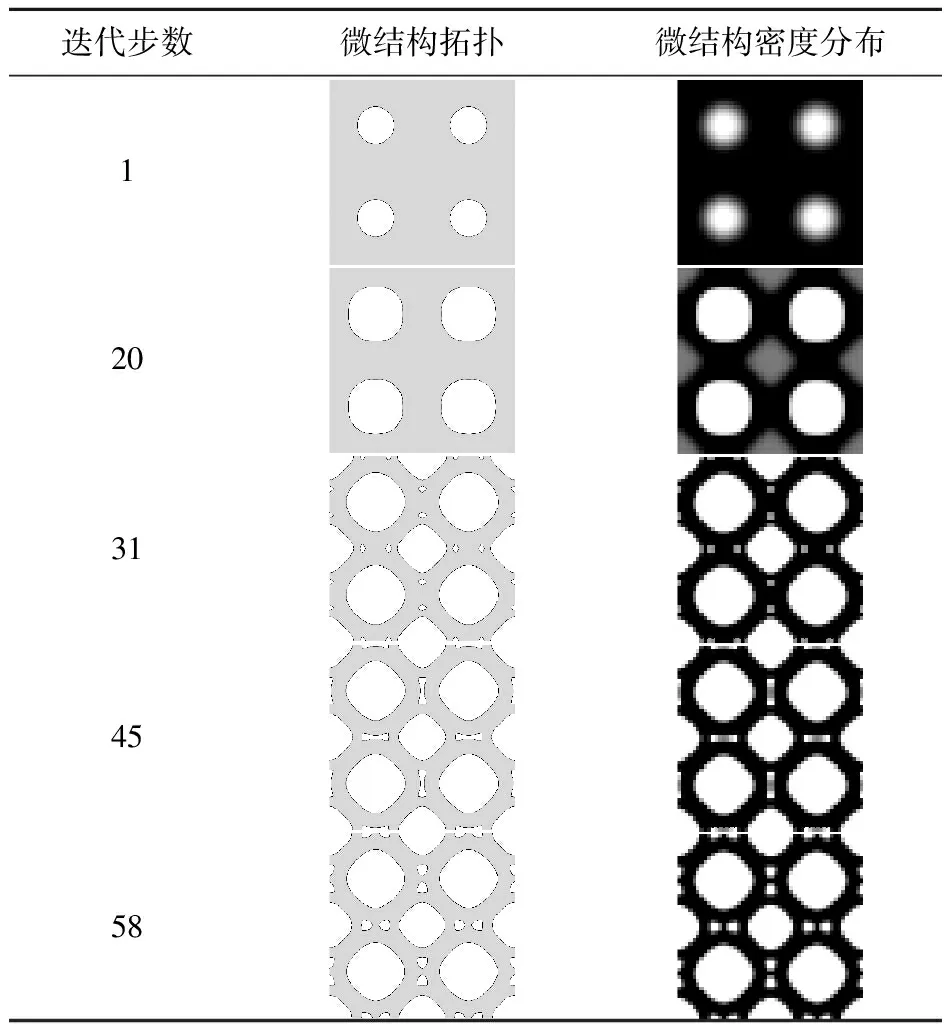
表1 體積模量最大化優(yōu)化過程

最終優(yōu)化的微結(jié)構(gòu)等效彈性剛度矩陣如下，體積模量值為0.190。

為了進一步驗證所得體積模量的最優(yōu)，在此引入復(fù)合材料設(shè)計的HS(Hashin-Shtrikman)邊界[20]，該理論用于預(yù)測復(fù)合材料宏觀等效特性的界限值，可表示為

(19)

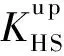
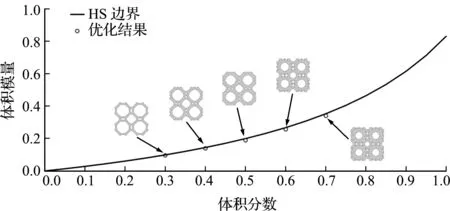
圖5 優(yōu)化結(jié)果與HS邊界值對比

表2列出了在不同初始設(shè)計下，體積分數(shù)為0.5，是否引入水平集帶方法的優(yōu)化結(jié)果比較。在部分情況下，引入水平集帶方法能獲得更合理的優(yōu)化結(jié)果。對于較為簡單的體積模量最大化問題，迭代過程中拓撲變化較小，水平集帶方法對優(yōu)化結(jié)果的提升并不明顯。

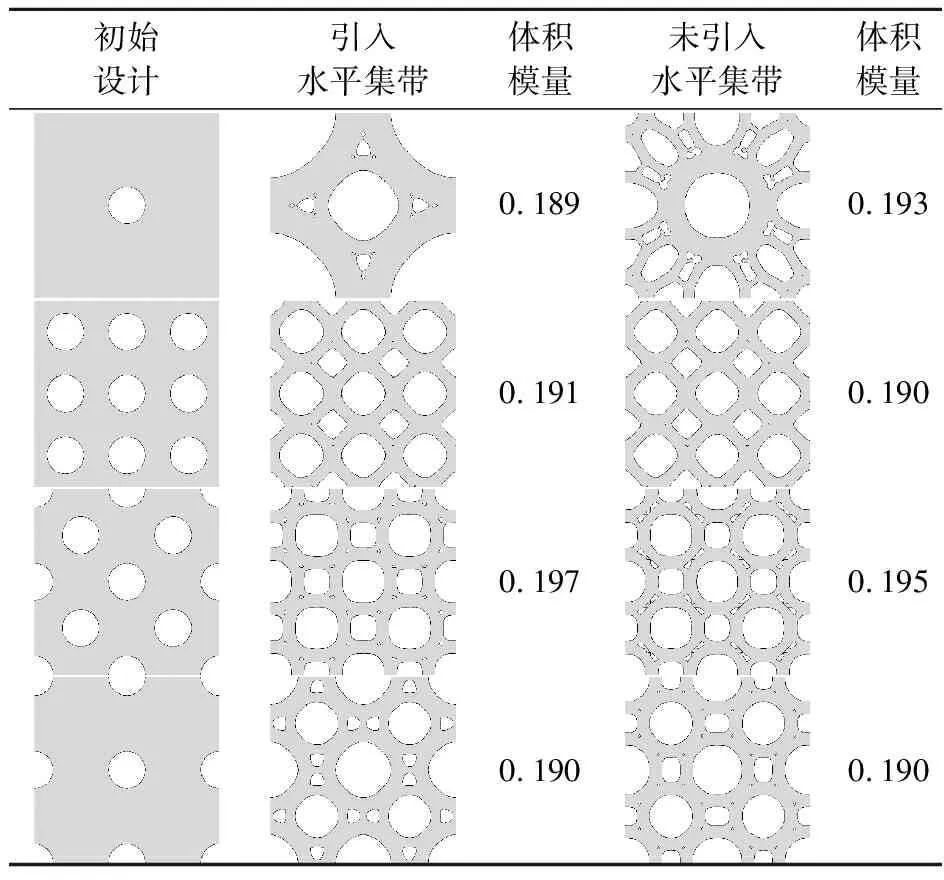
表2 不同初始設(shè)計的優(yōu)化結(jié)果

最終的優(yōu)化結(jié)果對于初始設(shè)計和優(yōu)化參數(shù)都比較敏感，說明了材料設(shè)計問題具有較多的局部最優(yōu)解，呈現(xiàn)明顯的非凸性[3]。這是因為定義的目標函數(shù)式(15)同時與等效彈性矩陣的4項數(shù)值相關(guān)，同一目標函數(shù)值可能對應(yīng)著4項數(shù)值不同的搭配，也對應(yīng)著不同的等效彈性剛度矩陣和微結(jié)構(gòu)拓撲，這也說明微結(jié)構(gòu)拓撲與剛度矩陣并非一一對應(yīng)的關(guān)系，從而導(dǎo)致具有眾多局部最優(yōu)解。

4.2 剪切模量最大化

以剪切模量最大化為目標函數(shù)，水平集帶初始帶寬為3，每次迭代減小0.1，最終收斂至0。表3列出了優(yōu)化結(jié)果，包括各種初始設(shè)計和不同體積分數(shù)下(0.2,0.4,0.6)的微結(jié)構(gòu)拓撲、3×3微結(jié)構(gòu)分布及對應(yīng)的剪切模量值G。以剪切模量最大化為目標的優(yōu)化結(jié)果材料分布在45°斜對角線上，即與切應(yīng)力平行的方向，說明材料得到了充分的利用。雖然不同初始設(shè)計下的微結(jié)構(gòu)拓撲不完全相同，但其周期性排列的形式是基本相似的，也側(cè)面說明了材料設(shè)計優(yōu)化結(jié)果的非唯一性。因此雖然材料設(shè)計的優(yōu)化結(jié)果很大程度上取決于初始設(shè)計和優(yōu)化參數(shù)，但通過合理選擇模型和方法仍可以獲得較優(yōu)的結(jié)果。

表3 不同初始設(shè)計和體積分數(shù)下的優(yōu)化結(jié)果Tab.3 Optimal results under different initial designs and volume fraction

4.3 負泊松比材料

為了獲得具有負泊松比性質(zhì)的材料，以式(17)為目標函數(shù)，取體積分數(shù)為0.4，對各種初始設(shè)計，及是否引入水平集帶方法進行對比。針對更為復(fù)雜的負泊松比問題，為了提高迭代穩(wěn)定性[18]，在此處設(shè)置水平集帶初始帶寬為6，每次迭代減小0.05，最終帶寬收斂至0。表4列出了4種初始設(shè)計下的負泊松比優(yōu)化結(jié)果。負泊松比材料的獲得說明了本文方法和模型的有效性，且與文獻[21，22]有著相似的拓撲形式。橫向?qū)Ρ劝l(fā)現(xiàn)對于拓撲變化較大的負泊松比問題，引入水平集帶后能夠促進負泊松比的獲得，并且有著更小的泊松比。尤其是對于初始設(shè)計2，引入水平集帶后能夠避免求解陷入某些局部最優(yōu)解，最終收斂于更合理的結(jié)果。

圖6是表4初始設(shè)計2引入水平集帶方法的迭代收斂曲線。在前30步為了滿足體積分數(shù)約束，體積分數(shù)和目標函數(shù)迅速變化，結(jié)構(gòu)拓撲發(fā)生顯著變化，當(dāng)滿足體積約束后曲線趨于平穩(wěn)并最終達到收斂條件，說明本節(jié)所采用的材料設(shè)計方法具有較高的優(yōu)化效率。

表4 負泊松比優(yōu)化結(jié)果Tab.4 Optimal results with negative Poisson’s ratio

為了展示及驗證微結(jié)構(gòu)的負泊松比特性，將上述算例的3×3分布形式導(dǎo)入ANSYS進行分析。該模型尺寸為150 mm×150 mm。對模型左右兩端約束其豎向位移并分別施加向左向右的拉伸位移0.5 mm。結(jié)果如圖7所示，黑色實線和灰色云圖分別為變形前后結(jié)果。在左右施加拉伸位移后，上下兩端均產(chǎn)生了向外膨脹的位移，說明了由該微結(jié)構(gòu)周期排列形成的材料具有負泊松比的性質(zhì)。取圖7黑色虛線框內(nèi)的單胞進行分析，其左右兩側(cè)平均位移為0.170 mm，上下平均位移為0.105 mm，計算泊松比約為-0.612，與算例結(jié)果-0.607相近，也說明了本文采用的能量均勻化方法的有效性。

圖7 負泊松比仿真分析

5 結(jié) 論

本文采用了參數(shù)化水平集方法，更新了水平集迭代格式，并結(jié)合水平集帶方法，以材料的體積模量、剪切模量最大化和負泊松比為目標進行了微結(jié)構(gòu)拓撲優(yōu)化設(shè)計。優(yōu)化結(jié)果表明，(1) 更新了迭代格式和引入水平集帶方法的參數(shù)化水平集方法具有較高的優(yōu)化效率和穩(wěn)定性，并且能得到清晰光滑的材料邊界；(2) 本文方法能夠根據(jù)目標函數(shù)有效地搜尋到滿足特定性能的材料微結(jié)構(gòu)；(3) 材料設(shè)計問題具有較多局部最優(yōu)結(jié)果，最優(yōu)的微結(jié)構(gòu)拓撲不具有唯一性；(4) 水平集帶方法對于拓撲變化較小的體積模量最大化問題的求解優(yōu)勢并不明顯，但對于復(fù)雜的負泊松比材料設(shè)計問題，具有避免求解陷入局部最優(yōu)解,從而獲得更合理結(jié)果的優(yōu)勢。

本文方法能在一定程度上減輕優(yōu)化結(jié)果對初始設(shè)計的依賴性，但并不能解決材料設(shè)計問題的非凸性。本文方法還可應(yīng)用于最大化能量吸收問題和功能梯度材料的拓撲優(yōu)化設(shè)計。

參考文獻(References):

[1] Torquato S，Haslach H W.Random heterogeneous materials:Micro -structure and macroscopic properties[J].AppliedMechanicsReviews,2002,55(4):B62-B63.

[2] Guedes J,Kikuchi N.Preprocessing and postprocessing for materials based on the homogenization method with adaptive finite element methods[J].ComputerMethodsinAppliedMechanicsandEngineering,1990,83(2):143-198.

[3] Sigmund O.Materials with prescribed constitutive parameters:An inverse homogenization problem[J].InternationalJournalofSolidsandStructures,1994,31(17):2313-2329.

[4] Challis V J,Roberts A P,Wilkins A H.Design of three dimensional isotropic microstructures for maximized stiffness and conductivity[J].InternationalJournalofSolidsandStructures,2008,45(14-15):4130-4146.

[5] Guest J K,JH Prévost.Design of maximum permeability material structures[J].ComputerMethodsinAppliedMechanicsandEngineering,2007,196(4-6):1006-1017.

[6] Guest J K,Prévost J H .Optimizing multifunctional materials:Design of microstructures for maximized stiffness and fluid permeability[J].InternationalJournalofSolids&Structures,2006,43(22-23):7028-7047.

[7] Sigmund O,Torquato S.Design of materials with extreme thermal expansion using a three -phase topology optimization method [J].JournaloftheMechanicsandPhysicsofSolids,1997,45(6):1037-1067.

[8] Cheng K T,Olhoff N.An investigation concerning optimal design of solid elastic plates [J].InternationalJournalofSolidsandStructures,1981,17(3):305-323.

[9] Cheng G D,Guo X.ε -relaxed approach in structural topology optimization [J].StructuralOptimization,1997,13(4):258-266.

[10] Liang Y,Cheng G D.Further elaborations on topo -logy optimization via sequential integer programming and Canonical relaxation algorithm and 128-line MATLAB code [J].StructuralandMultidiscipli-naryOptimization,2019,61(1):411-431.

[11] Osher S,Sethian J A.Fronts propagating with cur-vature -dependent speed:Algorithms based on Hamilton-Jacobi formulations [J].JournalofComputationalPhysics,1988,79(1):12-49

[12] Sethian J A,Wiegmann A.Structural boundary design via level set and immersed interface methods [J].JournalofComputationalPhysics,2000,163(2):489-528.

[13] Luo J Z,Luo Z,Chen L P,et al.A semi-implicit level set method for structural shape and topology optimization[J].JournalofComputationalPhysics,2008,227(11):5561-5581.

[14] Wei P,Wang M Y.Piecewise constant level set me -thod for structural topology optimization[J].InternationalJournalforNumericalMethodsinEnginee-ring,2009,78(4):379-402

[15] Otomori M,Yamada T,Izui K,et al.Matlab code for a level set -based topology optimization method using a reaction diffusion equation[J].StructuralandMultidisciplinaryOptimization,2015,51(5):1159-1172.

[16] Wei P,Li Z Y,Li X P,et al.An 88-line MATLAB code for the parameterized level set method based topology optimization using radial basis functions[J].StructuralandMultidisciplinaryOptimization,2018,58(2):831-849.

[17] Wei P,Yang Y,Chen S K,et al.A study on basis functions of the parameterized level set method for topology optimization of continuums[J].JournalofMechanicalDesign,2020,143(4):1-48.

[18] Wei P,Wang W W,Yang Y,et al.Level set band method:A combination of density-based and level set methods for the topology optimization of continuums[J].FrontiersofMechanicalEngineering,2020,15(3):390-405.

[19] Xia L,Breitkopf P.Design of materials using topology optimization and energy-based homogenization app -roach in Matlab[J].StructuralandMultidiscipli-naryOptimization,2015,52(6):1229-1241.

[20] Hashin Z,Shtrikman S.A variational approach to the theory of the elastic behaviour of multiphase materials[J].JournaloftheMechanicsandPhysicsofSolids,1963,11(2):127-140.

[21] Amstutz S,Giusti S M,Novotny A A,et al.Topological derivative for multi-scale linear elasticity models applied to the synthesis of microstructures[J].InternationalJournalforNumericalMethodsinEngineering,2010,84(6):733-756.

[22] Wang Y Q,Luo Z,Zhang N,et al.Topological shape optimization of microstructural metamaterials using a level set method[J].ComputationalMaterialsScience,2014,87:178-186.