多子域模式重復結構多目標拓撲優化

王浩軒， 吳 開， 杜建鑌

(清華大學 航天航空學院，北京 100084)

1 引 言

當今微電子和航空航天等高新工業領域的發展對結構的傳熱性能提出了更高的要求，電路的集成化和小型化使得熱傳導變得更加困難，如何對散熱材料進行優化設計，從而利用有限材料獲得更好的傳熱效果，對未來芯片的研究有重要的意義。在航空航天領域，高速飛行器伴隨著嚴重的氣動加熱現象，如何設計同時滿足力熱要求的結構，也是一個值得研究的問題。拓撲優化是一種較為先進的優化方法，可以改變結構的拓撲構型，有很大的設計自由度，目前已廣泛應用于力、熱、聲和振動等多種領域的優化當中。

工程中傳熱問題大多是連續體拓撲問題，對于連續體拓撲優化，早期最重要的開創性工作可追溯到20世紀80年代初Cheng等[1,2]針對板的優化設計研究。Bends?e等[3]通過設計域內材料分布描述拓撲微結構，基于均勻化理論將微結構構型與宏觀材料屬性對應。但均勻化計算較為復雜，之后文獻[4，5]發展了變密度拓撲優化方法，這種方法基于帶罰因子的固體各向同性材料插值模型SIMP(Solid Isotropic Material with Penalty)，對中間密度的材料進行懲罰，使優化迭代趨于0～1分布，這種方法程序實現簡單，優化效率高，應用范圍較廣。對于SIMP模型中的中間密度單元，Bends?e等[6]給出了原因和物理解釋。張君茹等[7]以SIMP法為基礎，以二次型性能指標為目標函數，提出了實現旋轉板減振設計的拓撲優化方法。牛飛等[8]以結構最小柔順性為目標函數，提出了擴散結構優化設計的理論模型，并得到了二維和三維算例的合理結果。此外，進化結構優化方法、獨立連續映射法ICM(Independent Continuous Mapping)和水平集方法等也有較為廣泛的應用。

對于傳熱問題，左孔天等[9]基于SIMP材料插值模型，編制了傳熱結構的多目標優化算法，通過數值算例進行了驗證。崔天福等[10]以密度法為基礎，推導出了滿足KKT(Karush-Kuhn-Tucker)條件的最優準則法迭代公式。龍凱等[11]基于ICM法，建立了周期性結構拓撲優化模型，針對不同循環周期下的算例進行計算和對比。魏嘯等[12]基于密度法，分別以算數平均溫度最小化、單位面積內能最小化以及平均溫度梯度最小化為目標函數，對高導熱材料分布形態進行了研究。Jing等[13]利用水平集法表示結構邊界，采用網格生成法逼近熱對流邊界，驗證了基于水平集的邊界表達優化設計方法的有效性。Torii等[14]提出了一種具有多項式混沌展開PCE(Polynomial Chaos Expansion)的熱傳導魯棒拓撲優化，給出了求解不確定大小、不確定位置的發熱問題以及不確定位置的損傷問題的應用，證明了基于不確定性的優化方法能夠獲得更穩健的設計。Lohan等[15]利用生成算法對傳熱問題拓撲結構進行設計，表明生成算法相對于SIMP方法有更大的設計空間。

模式重復的思路來自于超材料的設計，超材料是一類人工復合材料或結構，其特點是具有周期性重復微結構。目前超材料的設計廣泛使用拓撲優化方法，如Sigmund等[16]利用變密度法設計的負熱膨脹系數超材料以及Christiansen等[17]設計的負折射率超材料。但目前大部分超材料設計均是材料級設計，即設計單胞尺寸遠小于宏觀尺寸。這種設計需要引入均勻化方法，且實際工程中限于制造精度，難以實現真正的材料級設計。而微結構尺寸與宏觀尺寸相當的結構級微結構設計目前僅在仿生材料[18]領域有較廣泛的應用，且單胞結構依賴于主觀設計，受限嚴重。因此利用拓撲優化進行結構級超材料設計，在工程中是一個新的嘗試。Liu等[19]討論了一種基于對稱性和模式重復的水平集拓撲優化方法，相較傳統水平集方法減小了數值計算量，通過數值算例驗證了方法的可行性和有效性。Wu等[20]提出了基于變量關聯方法超材料柔性機構設計方法，獲得了具有更高強健性的多胞柔性機構。

本文針對工程中的傳熱模式，以SIMP模型為基礎，利用多子域不同分布來實現多種模式重復方案，對傳熱結構進行優化。現階段傳熱領域大多以散熱弱度為目標函數，本文考慮了工程中出現較多的局部溫度優化問題，以局部溫度最小化為優化目標進行設計。為了獲得綜合能力更強的結構，引入了多目標設計方法，對散熱弱度和局部溫度同時進行優化，避免了優化結果中的異常現象。同時考慮工程中的力熱一體化問題，利用多目標方法，同時對結構散熱弱度和靜柔度進行優化。最后比較了模式重復結構和傳統全域設計結構在缺陷影響下的性能。

2 理論模型與優化方法

2.1 模式重復設計模型建立

模式重復方法本質上是引入周期約束，將單個或多個設計域上的設計變量映射到全域上，目前研究較多的是單設計域映射方式，本文參考并發展了Wu等[20]提出的多設計域映射模型，并將其應用于熱傳導以及力-熱一體化多目標優化問題。

考慮模式重復的單域設計和多子域設計概念模型如圖1所示。將全域劃分為大小相等的周期性單胞，單域模式重復的設計變量定義在其中一個單胞上；多子域模式重復的設計變量定義在其中多個單胞上，最后通過全等映射復制到其他單胞(由同種單胞映射而成的區域為一個子域)。

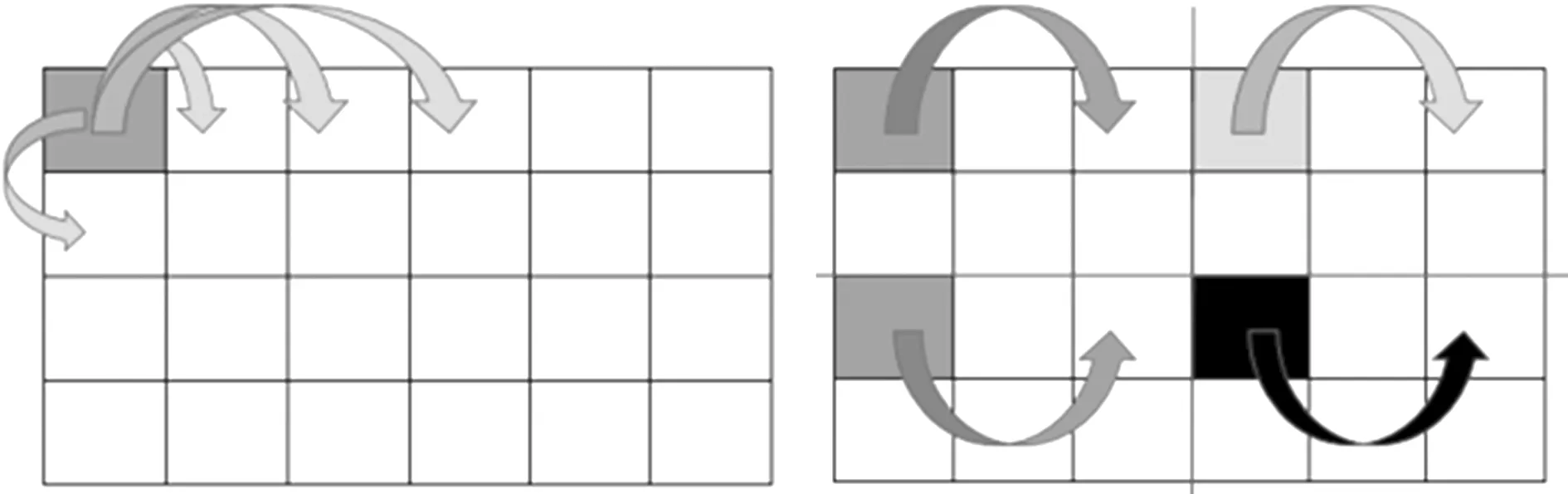
圖1 考慮模式重復的單域和多子域設計的映射方式

首先以熱傳導拓撲優化問題為例，引入模式重復的拓撲優化模型可表示為

s.t.:KT=P

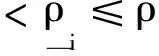
(1)

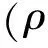
(2)

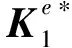
(3)

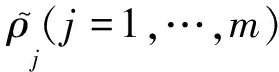
(4)

式中r為過濾區域的半徑，α與迭代步數有關，可行的一種形式為α=max [1,(t-t0)]，t和t0分別為當前和迭代穩定時的迭代步數，目的是在迭代穩定后逐步減小過濾的影響。

2.2 最優條件與迭代求解

由拉格朗日乘子法易得式(1)的最優條件為

(i=1,…,n)

(5)

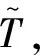
(6)

式中L為局部溫度選擇向量。由伴隨法進行靈敏度分析，目標函數靈敏度可表示為

(7)

式中λ為目標函數增廣拉格朗日函數的拉格朗日乘子。對于兩種目標函數，λ可得

(8)

由于K只顯含物理密度x，因此其對設計變量以鏈式求導法則進行靈敏度分析，可表示為

(9)

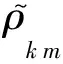
(10,11)

(12)

同樣可以給出,

(13)

(i=1,…,n)

(14)

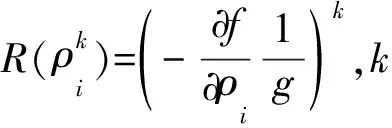
(15)

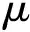
2.3 多目標優化模型和求解

多目標模型可利用加權方式將不同目標綜合在一個目標函數當中，為保證優化中不同目標具有量級相近的變化率，可利用式(16)對散熱弱度和局部溫度進行加權處理[9]

(16)

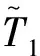
s.t.:S=PTT

KT=P

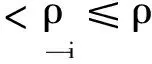
(17)

此時目標函數靈敏度分析結果如下,

(18)

根據式(7，8)可求出。

3 問題與結果分析

3.1 均布內熱源散熱問題

考慮芯片散熱的背景材料發熱問題，全域尺寸為0.1 m×0.1 m，下邊界中心有1/2長度的對流邊界，其余邊界絕熱。兩種設計材料導熱系數分別為λ1=398 W/(m·K)，λ2=237 W/(m·K)，對應銅和鋁，設定銅的體積約束為30%，這是雙材料優化問題。對流邊界換熱系數h=2000 W/(m·K)，內部均勻熱源Q=2.4×105W/(m2·K)，外部環境溫度T∞=20 ℃，優化目標為散熱弱度。

全域設計優化結果中，高導熱材料(銅)基本都堆積在拓撲結構的下方，可以解釋為整個區域的熱量向此處集中，因此需要在此處鋪設高導熱材料以更高效地將熱量導出。圖2展示了全域設計、不同結構單胞數的單域設計和不同映射方案的多子域設計優化結果(不同方案Sx-y中，x為子域的個數，y為設計單胞的映射類型，具體分布如圖8所示，不同顏色代表不同的子域)。可以看出，全域設計與模式重復設計之間，以及不同模式重復方案之間的拓撲結果有較大差異。這種差異產生的原因是模式重復方案引入了周期約束，而且不同映射方式也會影響優化效果。

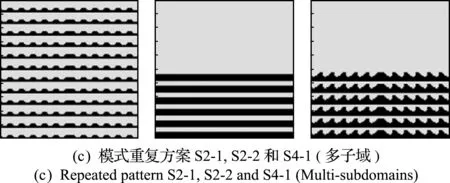
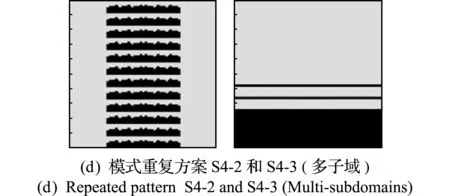
圖2 均勻內熱源散熱問題優化結果

為探究其中的聯系，將不同映射方案和不同結構單胞數對應的拓撲結構下的散熱弱度進行比較，如圖3所示。橫坐標表示每個方向上單胞的個數，縱坐標為對應優化結果的散熱弱度。比較全域設計和模式重復可以看出，全域設計結果總是最優的，因為其具有最高的設計自由度；比較不同模式重復方案，此算例中多子域模式重復結果均優于單域模式重復結果，但并不是子域越多越好，與設計域映射方式有關。優化效果較好的三種方案為S2-2，S4-1和S4-3，具體分布如圖2(c，d)所示。共同點是，(1) 材料整體處于結構下方，與全域設計相似； (2) 子域近似按照全域設計結構分區，保證了不同區域的不同需求。這對多子域模式重復的設計域映射方式有很好的借鑒作用。

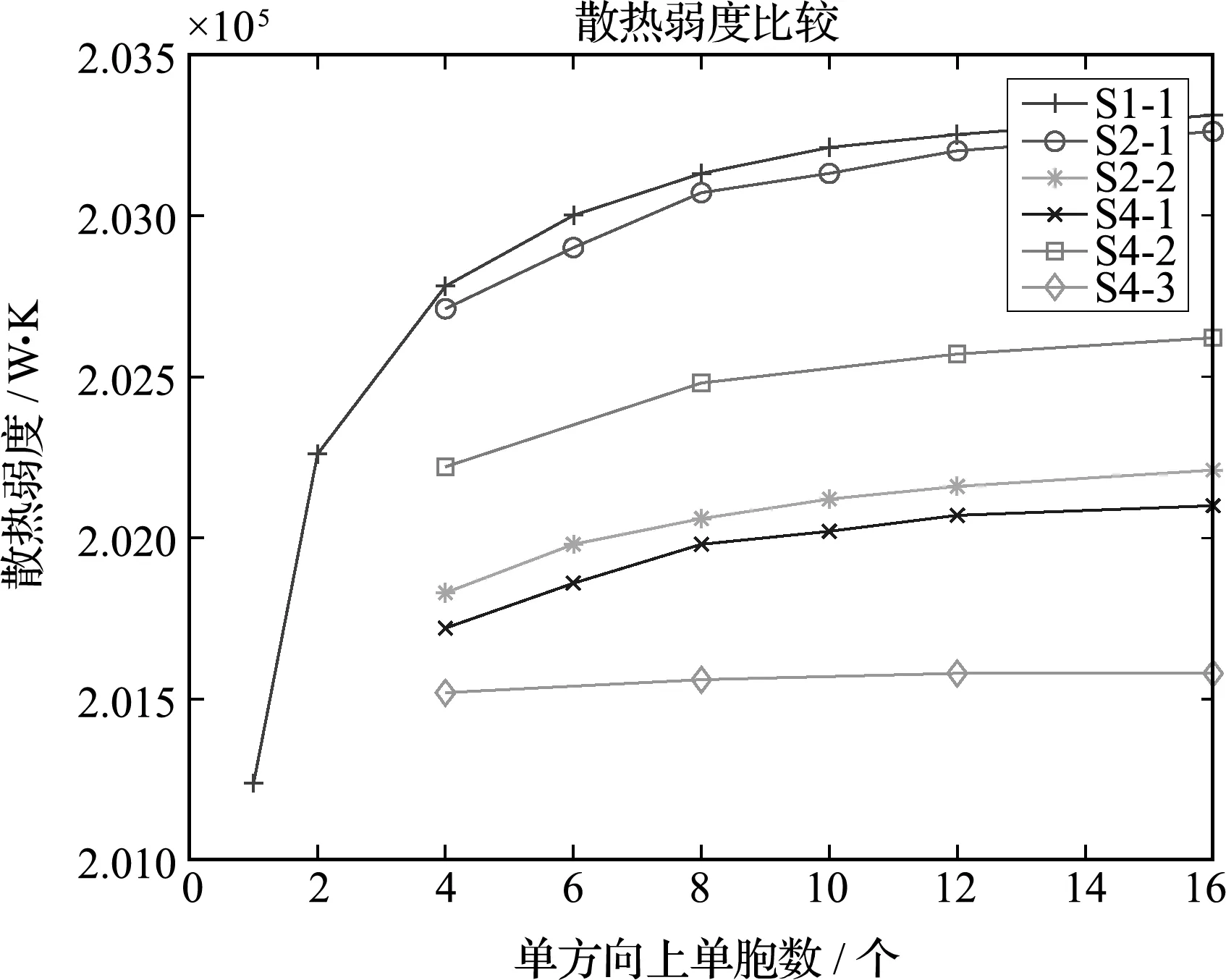
圖3 不同方案和單胞數的比較

3.2 恒定熱流局部溫度優化問題

以溫度作為目標函數時，可以選擇整個區域和局部區域甚至某幾個點的溫度進行優化，相較于散熱弱度，可以針對特殊情況進行處理，如目標區域某個部分有耐熱性差的材料，或是元件對溫度較為敏感，則需要特別針對這部分進行局部優化。

全域模型如圖4所示，發熱元件位于全域上方，將其簡化為恒定熱流邊界，長度為上邊界尺寸的1/2，需通過設計散熱通道將熱量傳導至下方對流邊界。全域尺寸0.1 m×0.1 m,恒定熱流q=20000 W/m，下邊界為對流邊界，其余邊界絕熱。兩種設計材料導熱系數分別為λ1=398 W/(m·K)，λ2=0.01 W/(m·K)，對應銅和空氣，銅的體積約束為50%。對流邊界換熱系數h=2000 W/(m·K)，外部環境溫度T∞=20 ℃。區域中央為一正方形保護區域，即需要進行局部溫度優化的區域，占全域面積的1/4。

圖4為全域設計優化結果，材料分為兩部分，一部分分布在兩邊，將熱流由上至下傳至換熱邊界；另一部分在中央，將目標區域的熱量導出。 這種結構的優勢是保護區域溫度極低，幾乎等于環境溫度，但不足之處是在熱流入口處出現局部高溫。

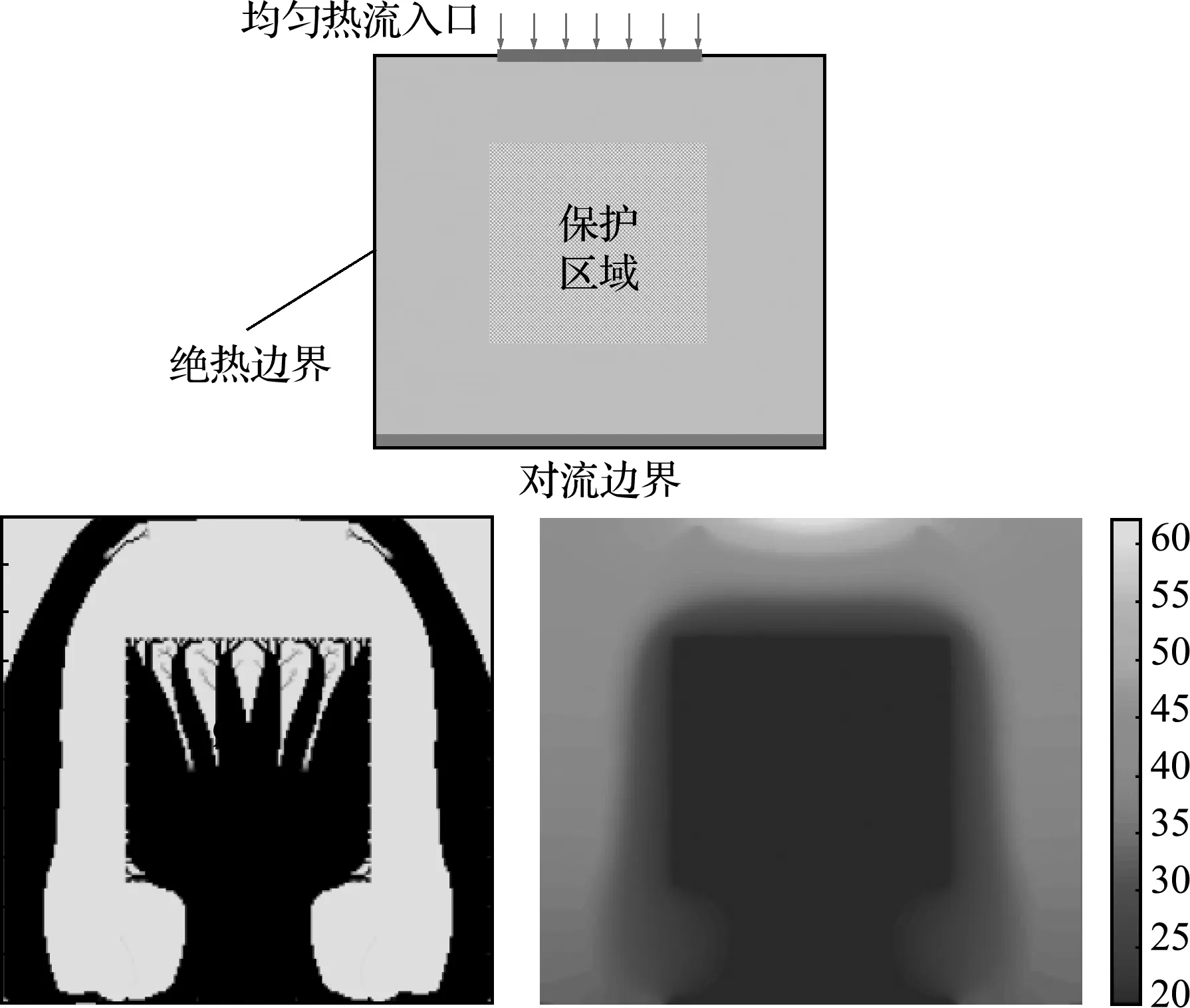
圖4 簡化模型和全域設計結果

由于優化目標和邊界條件的特殊性，通過以下處理保證模式重復結果的合理性，令熱流入口處單元密度恒為1，且不隨迭代變化，可以保證熱流能夠進入區域，與實際工程也相符。利用多目標優化公式將散熱弱度和保護區域溫度聯合，散熱弱度為低權重，目的是防止非保護區域溫度異常；保護區域溫度為高權重，使保護區溫度最小化。

不同模式重復拓撲結構如圖5所示，相關參數列入表1。與問題1的相同點是模式重復結構優化效果均差于全域設計結果，而且溫度相差較為明顯，但此問題中全域設計結果在非保護區域出現明顯高溫，而這樣的高溫在工程應用中可能會受到很大限制。

圖5 不同方案拓撲優化結果

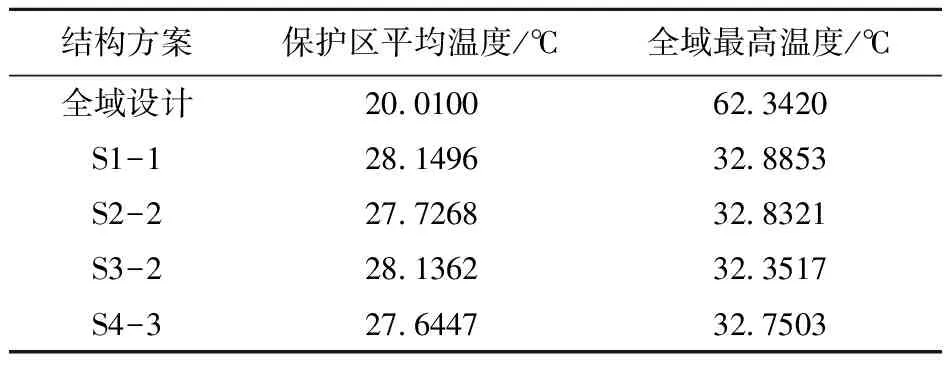
表1 不同方案參數

模式重復結構將熱流邊界與保護區域直接相連，這是模式重復結構與全域設計結構的最大不同之處。在模式重復中，即使考慮了將保護區域設為單獨的子域(圖5(b)左)，仍然無法避免這種直接相連的情況。這與模式重復方法本身的周期性約束有關，在這種約束下，模式重復方法對特定問題(如本節的局部溫度優化)適應性較差。但是模式重復結構中，材料在全域內分布較均勻，這種結構更容易兼顧多種性能，對實際工程的復雜環境有較強的適應性。

3.3 力熱一體化結構設計問題

力熱一體化結構的優化設計可以對工程中復雜的力熱一體化問題提出設計思路。本節基于簡單的力熱條件模型，探究模式重復在力熱一體化結構設計中的可行性。

如圖6所示，全域尺寸0.1 m×0.05 m，熱邊界條件為區域上邊界中心有1/2長度的恒定熱流邊界，qh=20000 W/m，下邊界為對流邊界，換熱系數h=2000 W/(m·K)，其余邊界絕熱，外部環境溫度T∞=20 ℃。力邊界條件，上邊界中心有向下的集中力F=1000 N，下邊界左右角為固定邊界。設計材料為鋁合金，體積約束30%。導熱系數λ=160 W/(m·K)，彈性模量E=72 GPa，泊松比為0.33。熱目標與力目標分別是散熱弱度和靜柔度，為多目標優化問題。

圖6為簡化模型以及不同力熱權重下的全域設計結果，由于結構是左右對稱的，方便起見只展示左半結構。可以看出，隨兩者權重的變化，拓撲結構逐漸從傳力最優變化至傳熱最優。

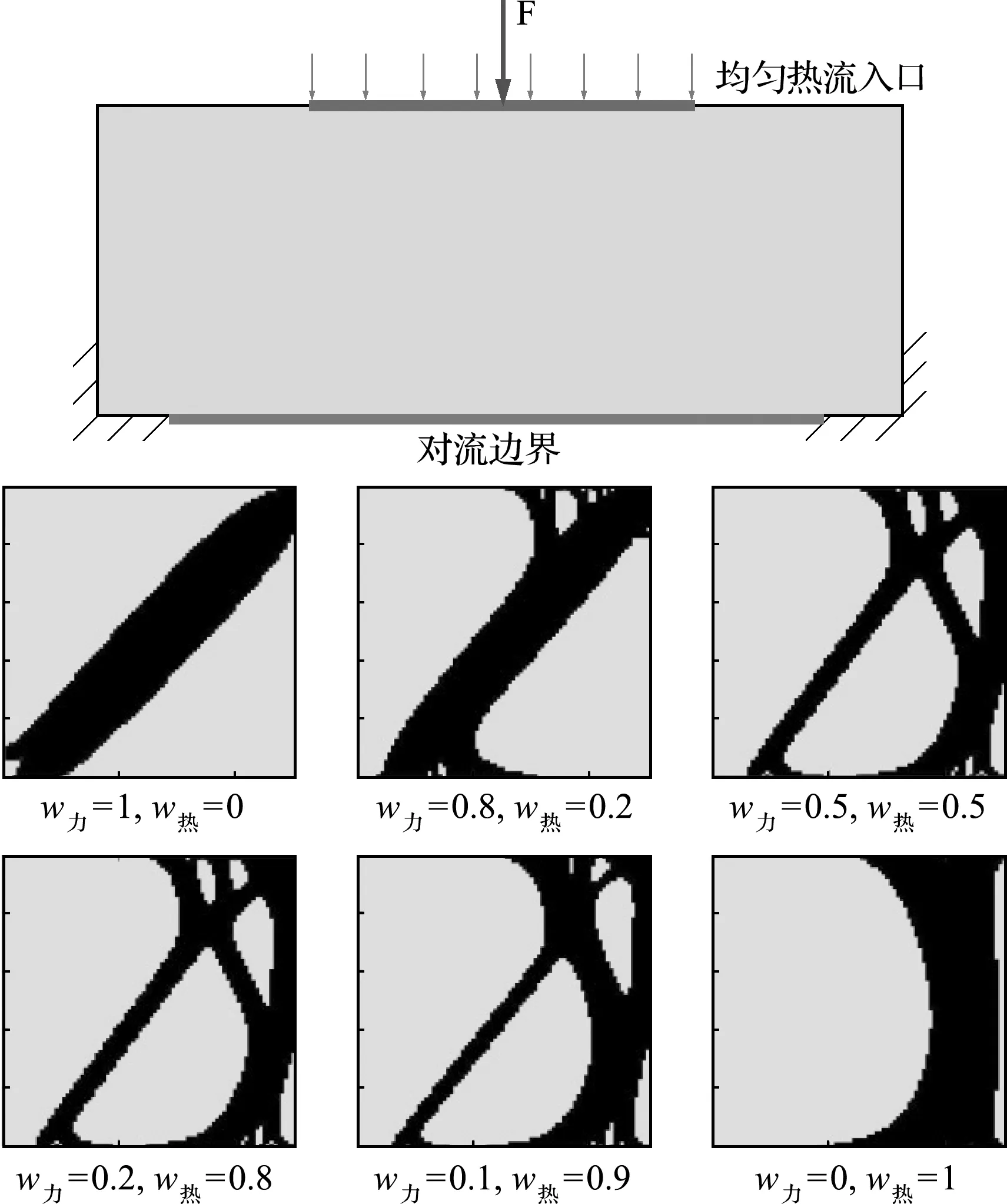
圖6 簡化模型和全域設計結果(左半)

模式重復結構也有類似的變化，不同重復方案的結果如圖7所示。當散熱弱度與靜柔度權重相當時，拓撲結構具有兩者單獨優化時的特征，可以看作是純力優化與純熱優化的結合。不同方案下，模式重復方法均得到了清晰的結構。

圖7 不同模式重復方案和不同權重組合結果(左半)

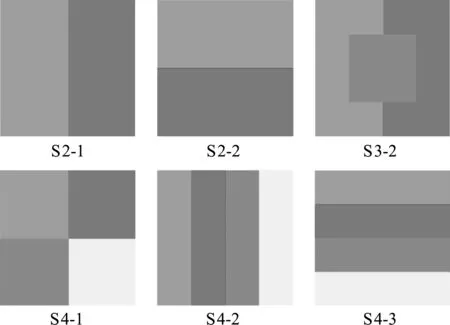
圖8 不同多子域模式重復映射方案(不同顏色為不同子域)

4 結構在缺陷影響下的性能

分析全域設計結構和模式重復結構在受損狀態下的性能。分析方式主要為全局分析，假設 0.1 m×0.1 m的結構上(如3.2節)出現了一小塊缺陷，缺陷大小為0.0167 m×0.0333 m(結構1/6邊長×1/3邊長)，缺陷處材料設置為低性能材料。缺陷橫縱坐標均進行變動，以遍歷整個區域。每一組坐標為一個采樣位置，記錄此缺陷下結構的目標函數和全域最高溫度等信息，得到一系列樣本數據，進而對樣本數據進行分析。以3.2節得到的最優結構為例，統計得到的樣本數據標準差列入表2。

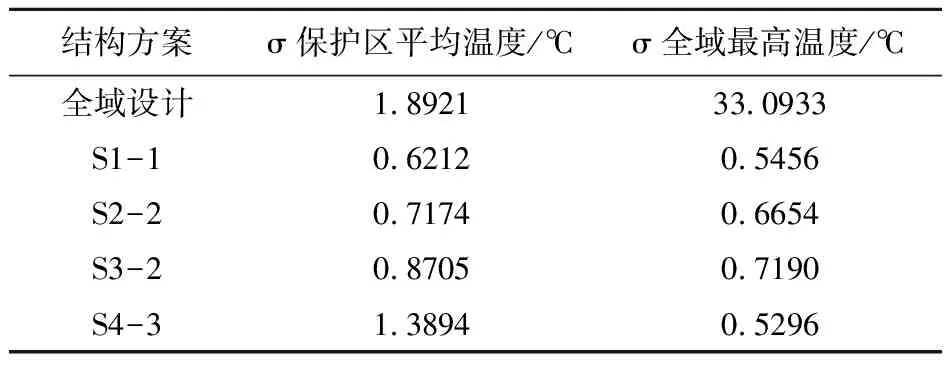
表2 恒定熱流局部溫度優化問題結構強健性分析

對恒定熱流局部溫度優化問題不同結構進行分析，發現不同結構中，全域設計的保護區平均溫度和全域最高溫度的標準差明顯高于其他結構，說明全域設計結構在有缺陷影響時，性能波動較大，這是因為全域設計結構關鍵位置破壞后，熱量會在上方集中，而模式重復結構由于每個單胞都有工作能力，因此不會存在這樣的情況。則可以說明模式重復結構具有更強的抗缺陷能力。

5 結 論

本文通過兩類傳熱結構設計,以及力熱一體化結構設計，驗證了多子域模式重復方法在熱傳導和力熱一體化拓撲優化中的可行性。對以溫度為目標函數的傳熱問題進行了分析，考察了多子域模式重復方法對局部優化問題的適應能力。最后比較了全域設計結構和模式重復結構在缺陷下的性能。

從優化效果看，模式重復設計與傳統全域設計相比有較大差距，這主要是因為模式重復方法大大減小了設計自由度。但另一方面，模式重復有很多適合工程應用的特性和功能, (1) 模式重復結構由周期性微結構單胞排列而成，這為工程的模塊化組裝提供了基礎，大大降低了制造難度。(2) 模式重復結構更擅長應對缺陷問題，即使局部失效，整體性能也不會受到太大影響。(3) 模式重復結構綜合性能較為均衡，在多目標因素均衡設計中有很大應用空間。

多子域模式重復設計效果介于單域模式重復設計和傳統全域設計之間，同時又繼承了模式重復結構的諸多優點，因此是一種十分理想的模式重復方案。當然，多子域模式重復方法目前仍存在一定的不足。(1) 多子域模式重復中，子域的映射方案主要依靠經驗和嘗試，如參考全域設計結果和利用多子域均勻分布等，尚不能高效準確地進行最優映射。 (2) 多子域模式重復結構中存在結構冗余，這也是其性能相比全域設計有所降低的原因之一。 (3) 多子域模式重復方案對一些特定問題的適應性較差，實際應用中仍需根據具體需求選擇全域設計或是模式重復設計。

參考文獻(References):

[1] Cheng K T,Olhoff N.An investigation concerning optimal design of solid elastic plates [J].Interna-tionalJournalofSolidsandStructures,1981,17(3):305-323.

[2] Cheng K T,Olhoff N.Regularized formulation for optimal design of axisymmetric plates [J].InternationalJournalofSolidsandStructures,1982,18(2):153-169.

[3] Bends?e M P,Kikuchi N.Generating optimal topolo -gies in structural design using a homogenization method[J].ComputerMethodsinAppliedMechanicsandEngineering,1988,71(2):197-224.

[4] Bends?e M P.Optimal shape design as a material distribution problem[J].StructuralOptimization,1989,1(4):193-202.

[5] Rozvany G I N,Zhou M,Birker T.Generalized shape optimization without homogenization[J].StructuralOptimization,1992,4(3-4):250-252.

[6] Bends?e M P,Sigmund O.Material interpolation schemes in topology optimization[J].ArchiveofApp-liedMechanics,1999,69(9-10):635-654.

[7] 張君茹,程耿東.基于二次型性能指標定軸轉動板減振拓撲優化[J/OL].計算力學學報:1-8.[2021-07-26].http://kns.cnki.net/kcms/detail/21.1373.O3.20210408.1649.018.html.(ZHANG Jun-ru,CHENG Geng-dong.Topology optimization of vibration reduction of in-plane rotating plate around a fixed hub based on quadratic performance index[J/OL].ChineseJournalofComputationalMechanics:1-8.[2021-07-26].http://kns.cnki.net/kcms/detail/21.1373.O3.20210408.1649.018.html.(in Chinese))

[8] 牛 飛,王 博,程耿東.基于拓撲優化技術的集中力擴散結構設計[J].力學學報,2012,44(3):528-536.(NIU Fei,WANG Bo,CHENG Geng-dong.Optimum topology design of structural part for concentration force transmission[J].ChineseJournalofTheoreticalandAppliedMechanics,2012,44(3):528-536.(in Chinese))

[9] 左孔天,趙雨東,陳立平.傳熱結構的多目標拓撲優化設計研究[J].計算力學學報,2007,24(5):620-627.(ZUO Kong-tian,ZHAO Yu-dong,CHEN Li-ping.Study on multiple objective topology optimization of thermal conductive structure[J].ChineseJournalofComputationalMechanics,2007,24(5):620-627.(in Chinese))

[10] 崔天福,丁曉紅,侯麗園.基于密度法的傳熱結構拓撲優化設計[J].上海理工大學學報,2014,36(6):548-555.(CUI Tian-fu,DING Xiao -hong,HOU Li-yuan.Structural topology optimization design of heat transfer based on density method[J].JournalofUniversityofShanghaiforScienceandTechnology,2014,36(6):548-555.(in Chinese))

[11] 龍 凱,賈 嬌.基于ICM法的傳熱結構周期性拓撲優化設計[J].工程力學,2015,32(5):227-235.(LONG Kai,JIA Jiao.Periodic topology optimization design for thermal conductive structure using ICM method[J].EngineeringMechanics,2015,32(5):227-235.(in Chinese))

[12] 魏 嘯,丁曉紅.不同目標函數的傳熱結構拓撲優化研究[J].電子科技,2017,30(2):156-160.(WEI Xiao,DING Xiao -hong.Topology optimization of transfer structure for different objective functions[J].ElectronicScienceandTechnology,2017,30(2):156-160.(in Chinese))

[13] Jing G X,Isakari H,Matsumoto T,et al.Level set-based topology optimization for 2D heat conduction problems using BEM with objective function defined on design-dependent boundary with heat transfer boundary condition[J].EngineeringAnalysiswithBoundaryElements,2015,61:61-70.

[14] Torii A J,Santos D P D S,Medeiros E M.Robust to -pology optimization for heat conduction with polynomial chaos expansion[J].JournaloftheBrazilianSocietyofMechanicalSciencesandEngineering,2020,42(6):1-13.

[15] Lohan D J,Dede E M,Allison J T.Topology optimization for heat conduction using generative design algorithms[J].StructuralandMultidisciplinaryOptimization,2017,55(3):1063-1077.

[16] Sigmund O,Torquato S.Composites with extremal thermal expansion coefficients[J].AppliedPhysicsLetters,1996,69(21):3203-3205.

[17] Christiansen R E,Sigmund O.Designing meta material slabs exhibiting negative refraction using topology optimization[J].StructuralandMultidisciplinaryOptimization,2016,54(3):469-482.

[18] Ma Q,Cheng H Y,Jang K I,et al.A nonlinear mechanics model of bio-inspired hierarchical lattice materials consisting of horseshoe microstructures[J].JournaloftheMechanicsandPhy-sicsofSolids,2016,90:179-202.

[19] Liu Y,Li Z Y,Wei P,et al.Parameterized level-set based topology optimization method considering symmetry and pattern repe -tition constraints[J].ComputerMethodsinAppliedMechanicsandEngineering,2018,340:1079-1101.

[20] Wu K,Sigmund O,Du J B.Design of metamaterial me -chanisms using robust topology optimization and variable linking scheme[J].StructuralandMultidisciplinaryOptimization,2021,63:1975-1988.

[21] 杜建鑌.結構優化及其在振動和聲學設計中的應用[M].北京：清華大學出版社,2015.(DU Jian-bin.StructuralOptimizationandItsApplicationinVibrationandAcousticDesign[M].Beijing:Tsinghua University Press,2015.(in Chinese))