爆炸荷載下泡沫混凝土減振層動力響應分析

袁英杰，孫惠香，陳 卓

(空軍工程大學航空工程學院，西安 710038)

高精度鉆地武器的飛速發(fā)展促使人們愈發(fā)關(guān)注重要防護工程的抗打擊能力。天然巖石具有強度高、整體性好的特點，重要地下防護工程盡可能修建于整體性好、強度高的天然巖體中[1-3]。盡管如此，爆炸產(chǎn)生的強沖擊波仍會使結(jié)構(gòu)產(chǎn)生劇烈振動，造成人員傷亡和設備損壞。

近年來，國內(nèi)外學者針對地震荷載下結(jié)構(gòu)減振進行了大量研究[4-6]，其中，在襯砌與結(jié)構(gòu)層間設置減振層的方法體現(xiàn)了較好的適用性。黃勝等[7]比較了橡膠和泡沫混凝土材料隔振層的抗振效果，其中泡沫混凝土體現(xiàn)了更好的經(jīng)濟性；徐華等[8]比較了不同減振層設置模式，并建議采用軟質(zhì)減振層；王帥帥等[9]分析了隧道設置減振層后的應力變化，得出最優(yōu)減振層設計方法；崔光耀等[10]通過實驗研究了強振動下的減振層減振技術(shù)；趙武勝等[11]對泡沫混凝土減振層的減振效果影響因素進行了研究；針對地下結(jié)構(gòu)Wang等[12]、Zhao等[13]和Chen等[14]提出隔振層的隔振思想，隨后開展了相關(guān)理論分析和試驗研究；申玉生等[15]提出減振層結(jié)合柔性接頭抗振措施有效抑制了強振作用下交叉隧道的縱向裂縫擴展；李利莎等[16]對地下沖擊荷載下泡沫混凝土回填層的減振性能進行了研究，分析了結(jié)構(gòu)振動響應的影響因素。綜上，地下結(jié)構(gòu)設置減振層能起到良好的減隔振效果，而對爆炸荷載下的巖體拱結(jié)構(gòu)設置減振層減振效果的研究較少。

由于爆炸實驗的高危險、高成本的限制，對爆炸荷載下大型洞室結(jié)構(gòu)減振性能研究主要采用理論分析和數(shù)值模擬。本文基于ANSYS/LS-DYNA動力分析軟件，建立炸藥-空氣-結(jié)構(gòu)模型，在巖體與襯砌間設置0、0.2、0.4、0.6、0.8、1.0、1.2 m不同厚度泡沫混凝土減振層。應用流固耦合算法對比分析了襯砌重要控制點最大有效應力、峰值壓力及峰值位移，探究爆炸荷載下不同厚度減振層對結(jié)構(gòu)減振效果的影響，以期為巖體中洞室設計提供參考。

1 數(shù)值模擬

1.1 數(shù)值模型

計算模型：巖體中直墻拱結(jié)構(gòu)，跨度14 m，拱高6.5 m，其中直墻高2.0 m，埋深為10 m，巖體為Ⅲ類花崗巖。數(shù)值模型由圍巖、錨桿加固層、減振層、襯砌、空氣和炸藥組成。錨桿加固層指初期支護，為模擬實際工程效果，考慮初期支護提高了圍巖的強度、整體性等性質(zhì)，將加固層屈服應力、破壞應變及彈性模量增大20%[17]，寬度取2.0 m。減振層選擇可壓縮變形的泡沫混凝土，全斷面設置于加固層與襯砌層之間，厚度設置方案如表1所示。

表1 數(shù)值模擬方案

襯砌為鋼筋混凝土，雙層布筋，混合澆筑。考慮圍巖強度等級較高，自承載能力較好，同時為協(xié)調(diào)設置減振層后產(chǎn)生的變形，將地板與直墻分離設置，具體設置如圖1所示，鋼筋情況如圖2所示。

圖1 襯砌單元Fig.1 Lining elements

圖2 鋼筋單元Fig.2 Steels elements

工況為GBU-28型鉆地彈垂直侵徹洞室頂部，GBV-28技術(shù)參數(shù)如表2所示。根據(jù)以往經(jīng)驗公式總結(jié)出適合巖體的鉆地彈侵徹深度公式[18]，針對Ⅲ類圍巖，計算可得出GBU-28鉆地彈侵徹深度為4.85 m，本文取5.0 m。僅考慮武器爆炸對巖體中結(jié)構(gòu)的破壞作用，為封閉式爆炸，炸藥鉛垂置于巖體內(nèi)部，尖端距地面5.0 m。自重荷載遠小于爆炸荷載產(chǎn)生的作用，忽略重力影響[19]。考慮計算效率，縱深取2.0 m，對1/2模型建模。等效柱狀裝藥尺寸為0.3 m×0.3 m×2.1 m，TNT裝藥量為306 kg，中心起爆。對稱面施加相應對稱約束，除上表面外其他面設置無反射邊界，動力計算模型如圖3所示。

表2 GBU-28 技術(shù)參數(shù)

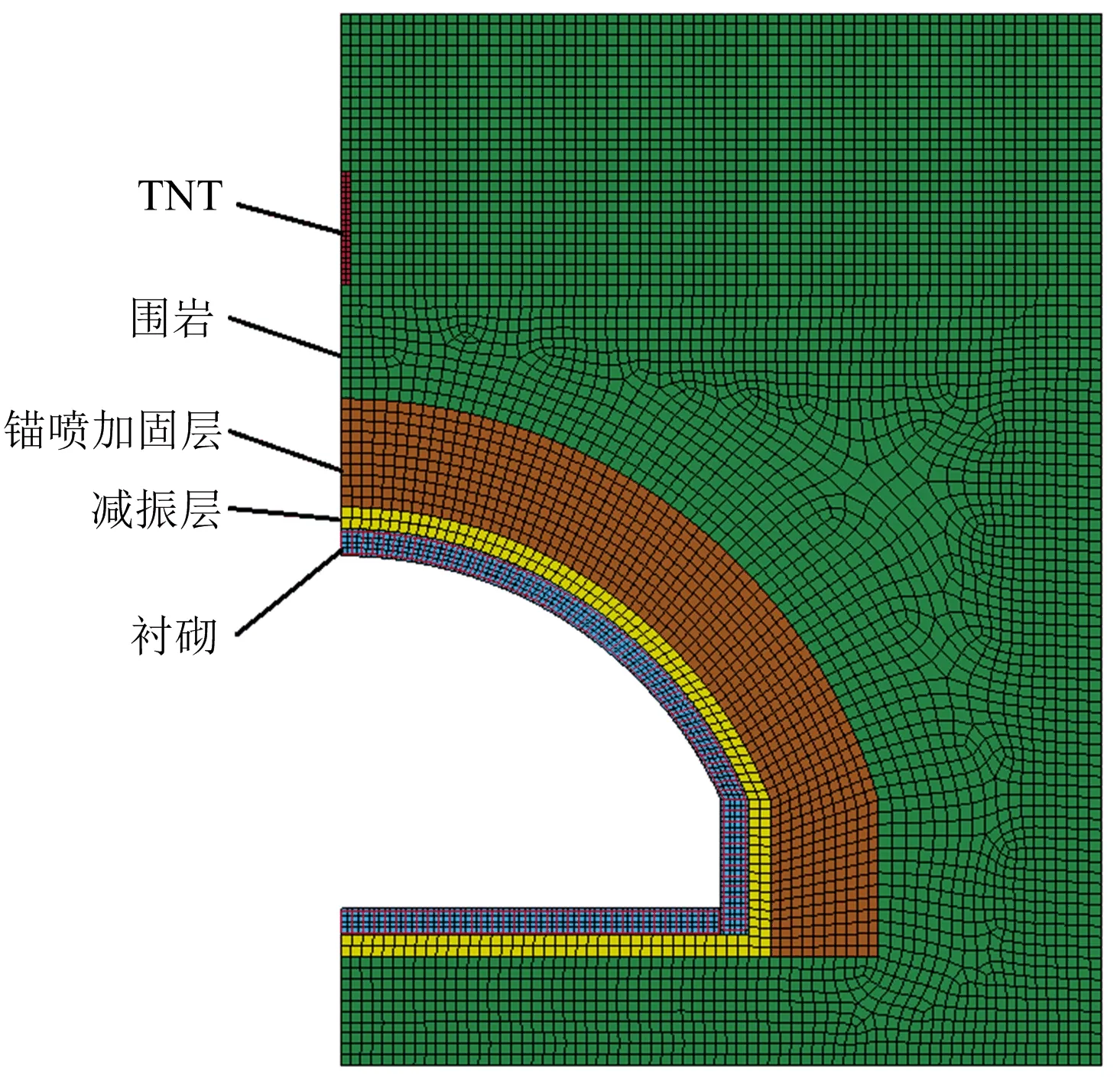
圖3 動力計算模型Fig.3 Dynamic calculation model

1.2 單元和材料模型

鋼筋單元類型為Link160,其他單元類型為3D Solid164。采用LS-DYNA中流固耦合算法描述爆炸的全過程，將空氣與炸藥定義為流體，炸藥可能膨脹的空間設置ALE空間，對于巖體、加固層、減振層和襯砌采用Lagrange算法，通過流固耦合方式處理炸藥對巖體及洞室的作用。襯砌與減振層采用接觸算法模擬二者相互作用[20]。

鋼筋、圍巖及加固層材料選用率相關(guān)塑性隨動強化模型(*MAT_PLASTIC_KINEMATIC)，參數(shù)見文獻[21]。混凝土采用H-J-C本構(gòu)模型，關(guān)鍵字為*MAT_JOHNSON_HOLMGUIST_CONCRETE，該模型能較好描述混凝土在爆炸荷載等高應變率下的力學行為，具體參數(shù)見文獻[22]。泡沫混凝土選用可壓縮泡沫模型*MAT_CRUSHABLE_FOAM，參數(shù)見文獻[16]。空氣采用*MAT_NULL模型和*EOS_LINEAR_POLYNOMIAL狀態(tài)方程描述，具體參數(shù)見文獻[23]。TNT炸藥采用*MAT_HIGH_EXPLOSIVE_BURN材料模型結(jié)合*EOS_JWL狀態(tài)方程描述，具體參數(shù)見文獻[24]。

2 模擬結(jié)果驗證

模型單元選取及不同單元壓力時程分別如圖4、圖5所示。為驗證結(jié)果的有效性，采用文獻[25]中計算公式。

圖4 單元選取Fig.4 Element selection

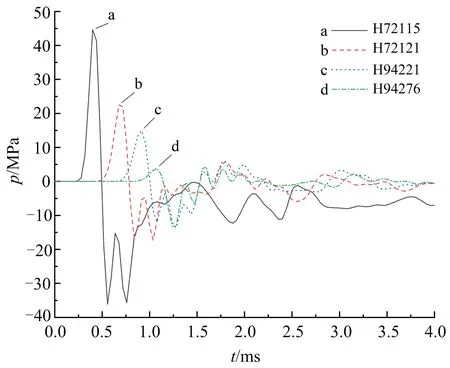
圖5 不同單元壓力時程Fig.5 Pressure-time at different elements

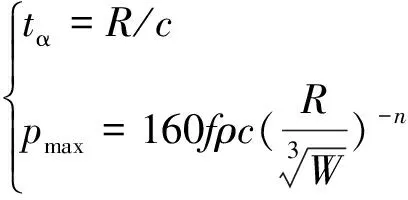
(1)

式中：tα為峰值到達時間；R為爆炸傳播距離；c為介質(zhì)中沖擊波波速；pmax為峰值壓力；f為耦合系數(shù)；ρ為巖石密度；W為裝藥質(zhì)量；n為介質(zhì)衰減系數(shù)。

數(shù)值模擬結(jié)果與公式結(jié)果誤差均在15%以內(nèi)(見表3)，誤差原因為等效柱狀裝藥與公式中裝藥方式存在差異，同時應力波穿過不同材料層發(fā)生反射，與初始應力波疊加也會造成誤差。

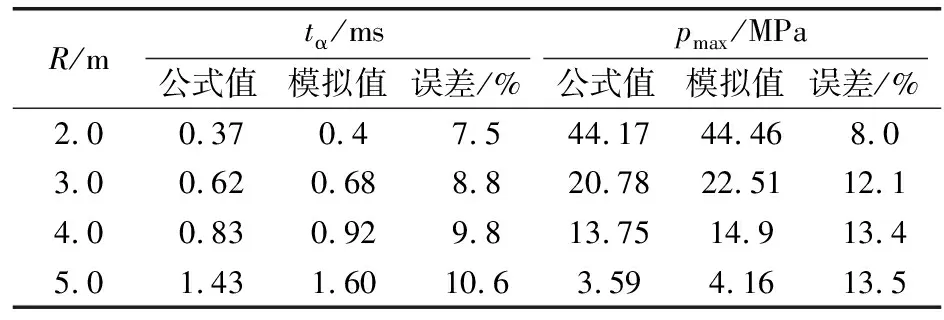
表3 不同位置巖石自由場沖擊參數(shù)

3 模擬結(jié)果分析

選取洞室襯砌外側(cè)拱頂、拱肩和拱腳單元，對比不同工況下最大有效應力、峰值壓力及峰值位移情況。

3.1 應力分析

混凝土在爆炸沖擊荷載下強度大于靜載作用下強度，其動態(tài)抗壓強度隨應變率增大而增大，根據(jù)歐洲國際混凝土學會建議，混凝土抗壓強度動態(tài)增強因子DIF按下式[26]計算：

(2)

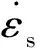
不同工況下最大有效應力如圖6所示，可知：①拱頂處由于距爆心最近，有效應力最大，未設置減振層時拱腳與拱頂接近，這是由于上部荷載主要通過拱腳傳至下部，拱肩有效應力最小；②設置減振層后拱頂與拱腳最大有效應力均變小，且拱腳最大有效應力減小超過80%，此時小于拱肩應力，這是因為拱腳下部的泡沫混凝土層改變了原有的剛性接觸，通過變形緩沖了拱腳傳遞的荷載，說明泡沫混凝土減振層改善了襯砌層的內(nèi)力情況，起到了減振作用；③設置減振層后拱肩最大有效應力提高不到21%，這是由于可壓縮的減振層使洞室各部分產(chǎn)生位移，而拱肩處于洞室上下連接部位，為協(xié)調(diào)內(nèi)部變形應力增大，但由于增幅不超過30%，可以忽略;④隨著減振層厚度的增加，拱頂與拱腳最大有效應力繼續(xù)減小，當減振層厚度超過0.6 m后，減振效果不明顯。

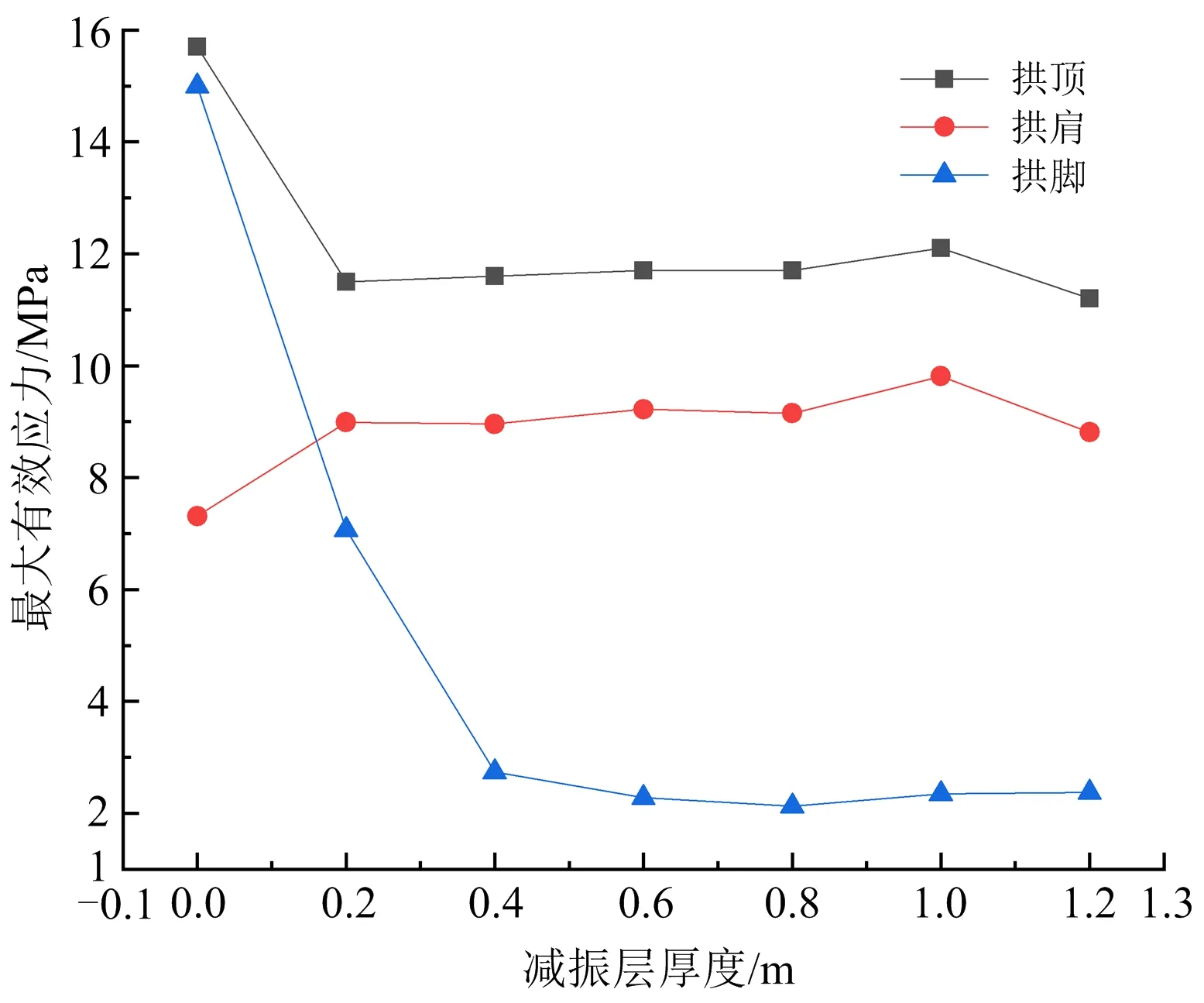
圖6 不同工況最大有效應力Fig.6 Maximum effective stress of different conditions

3.2 壓力分析

應力波從第1種介質(zhì)傳播至第2種介質(zhì)時，會在邊界處發(fā)生透射和反射現(xiàn)象，透射波與反射波的性質(zhì)由介質(zhì)的波阻抗(ρc)決定[27]。當(ρc)1>(ρc)2時，將發(fā)生反射卸載；反之發(fā)生反射加載。易知圍巖、混凝土、泡沫混凝土波阻抗依次遞減，選取分界面兩側(cè)不同材料單元進行壓力分析，如圖7所示。應力波由圍巖傳入泡沫混凝土時發(fā)生反射卸載，壓力變小，故圍巖中單元壓力絕對值均大于減振層中單元，如圖7a所示；之后應力波經(jīng)過減振層的衰減作用，再進入混凝土層時發(fā)生反射加載，壓力變大，故減振層中單元壓力絕對值大于襯砌單元，如圖7b所示，故應力波在減振層中衰減程度決定著襯砌受力大小。

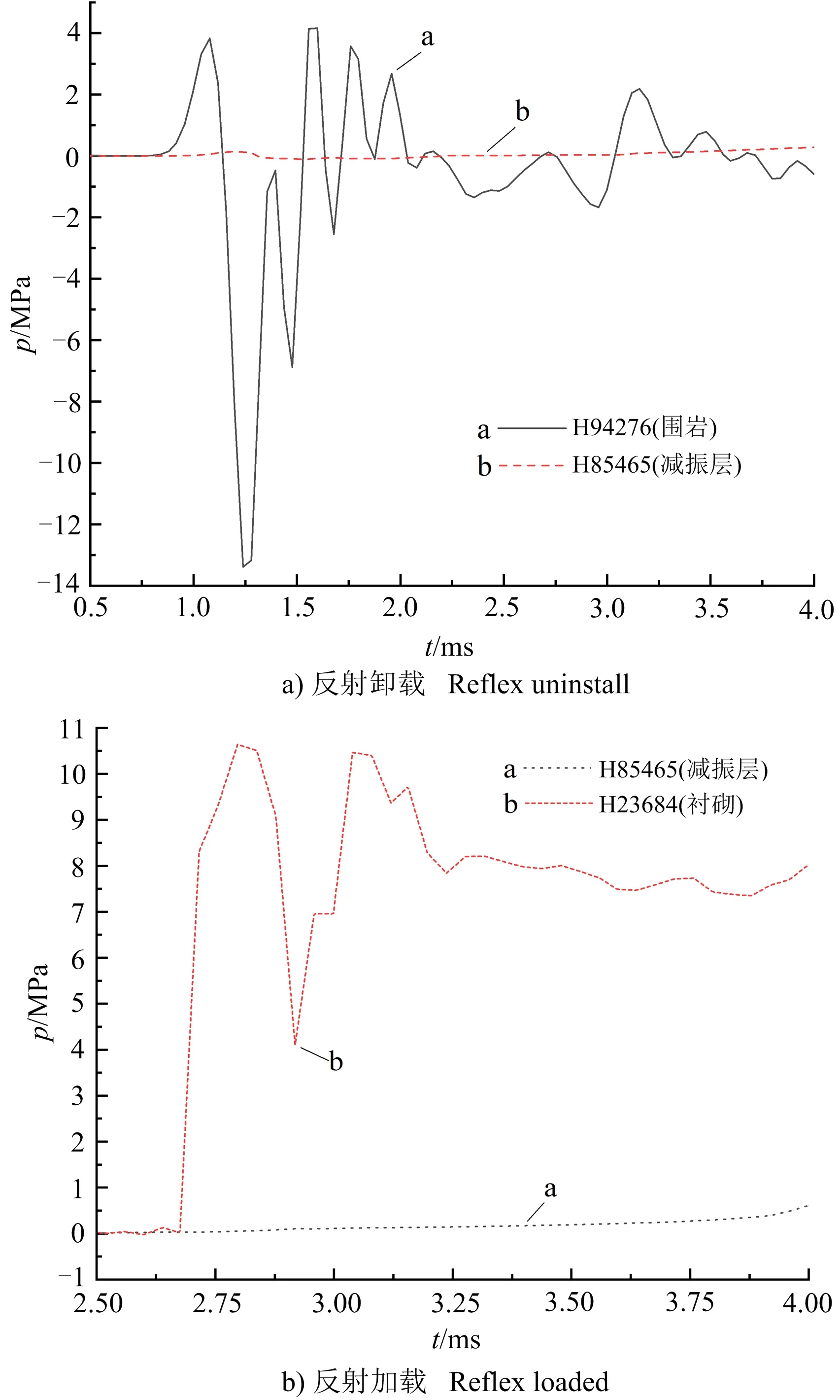
圖7 單元壓力時程Fig.7 Pressure-time of elements

隨著減振層厚度的增加，襯砌外層壓力普遍減小(見圖8)，說明泡沫混凝土層衰減應力波效果大于反射加載，起到了減振的作用；拱腳峰值壓力減幅最大，這是由于一方面上部減振層波阻抗較小，衰減了應力波，另一方面也有下部減振層緩沖上部荷載，改善拱腳受力；減振層厚度0.6 m時拱腳受力改善情況最好，已降至原來的15.4%，超過0.6 m后壓力衰減效果一般。

圖8 不同工況峰值壓力Fig.8 Maximum pressure of different conditions

3.3 位移分析

荷載施加過程中，應力波先后經(jīng)過拱頂、拱肩和拱腳，由拱腳將壓力傳至洞室下部材料。在未設置減振層時，拱腳與巖體剛性接觸，無法發(fā)生較大變形，故內(nèi)力較大；設置減振層后，應力波得到衰減，拱腳發(fā)生位移，吸收爆炸能量改善了襯砌受力情況(見圖9)。

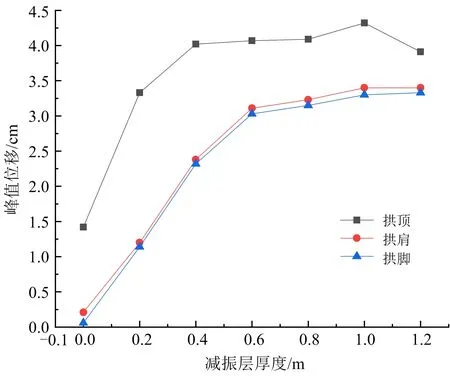
圖9 不同工況峰值位移Fig.9 Maximum displacement of different conditions

由圖9可以看出：①設置減振層后，襯砌各部分位移均增加，拱頂峰值位移最大，由1.45 cm增大到3.3 cm以上，拱肩與拱腳位移較小，拱肩略大于拱腳，整體位移控制在4.5 cm以內(nèi)，能確保洞室的安全；②拱肩與拱腳由內(nèi)加鋼筋的直墻連接，相對位移較小，隨減振層厚度增加峰值位移增加幅度變大，最后穩(wěn)定在3.0 cm左右；③隨著減振層厚度的增加，峰值位移繼續(xù)增大，當厚度超過0.6 m后，增加不明顯。

4 結(jié)論

1)設置泡沫混凝土減振層使襯砌有效應力減小，拱腳減少超過80%，起到了減振作用。

2)泡沫混凝土減振層衰減了應力波，減小了結(jié)構(gòu)受力，拱腳減少最為明顯，起到抗爆作用。

3)隨著層厚增加，最大有效應力、峰值壓力減小，峰值位移增大，超過0.6 m后變化不明顯。

4)力和位移兩個角度都是拱頂值最大，應采取措施對拱頂進行加固。結(jié)合經(jīng)濟因素考慮，建議設置0.6 m厚泡沫混凝土減振層。