注重思維能力的培養，讓復習課擺脫困境

邱丹

復習課是幫助學生進行查缺補漏，建立起完整知識結構的重要環節。復習課不只是單純地消化舊知識，不只是單純地做練習，更要注重對學生數學思維能力的培養。下面，筆者結合教學實踐，談談復習課的開展方式。

一、培養思維的靈活性——燃起學生學習熱情

在數學復習課中，不能因為沒有新的知識需要傳授，而取消了讓學生進行自主探究的環節。相反，因為復習課涉及舊知識的梳理，可以設置問題讓學生積極言說、大膽表達，這有利于學生間的思維碰撞，促進思維發展。

如人教版六下“圖形的運動”的總復習，筆者在課前通過任務單（讓三角形ABC通過圖形的運動變成一個美麗的圖案）讓學生運用學過的運動方式來設計圖形，激發學生靈活應用知識來設計作品。

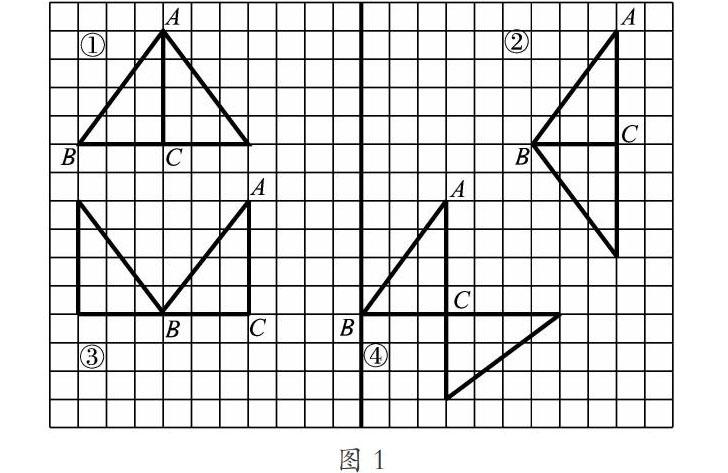
課伊始，筆者展示了學生的不同作品。在展示通過對稱軸來完成作品（圖1）時，筆者：同學們認真觀察，用同樣的三角形ABC怎么設計出來的軸對稱圖形會不一樣呢？生：因為它們的對稱軸不同，作品①是以AC為對稱軸，作品②是以BC為對稱軸。筆者：作品③和④的對稱軸，你們會尋找嗎？學生紛紛在草稿紙上畫了作品③和作品④的對稱軸。筆者：看來我們在觀察軸對稱圖形的時候，關鍵是要找到它的什么？生：對稱軸。

二、培養思維的深刻性——避免學生陷入題海

數學思維的深刻程度在解題的過程中表現得最為明顯，如果學生只是重復性地刷題，不懂得提煉題目中的知識信息，在遇到變式題時就可能因為找不到題目中的條件信息而不能正確地解決問題。因此，教會學生捕捉題中的信息，尋找信息間的聯系，揭示題目的本質，才能尋得最佳解題方法，使得思維更加深刻。

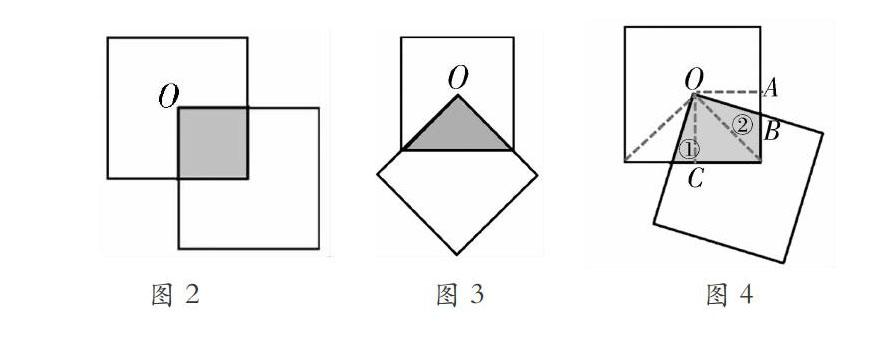
如“圖形的運動”的總復習，筆者通過多媒體展示了一道這樣的習題：兩個正方形紙片（圖2），其中一個正方形的一個頂點在另一個正方形的中心點O，繞點O轉動一個正方形，重疊部分的面積有什么變化嗎？本題的設計意圖是以“靜”觀“動”的方式刺激學生的觀察欲望，讓學生多角度深入觀察重疊部分的面積會隨著正方形的旋轉發生怎樣的變化。筆者操作圖形的轉動，引導學生從規則圖形入手，旋轉后重疊部分的圖形除了圖2，還有圖3的情況。學生觀察發現正方形在旋轉一周的過程中，圖2與圖3的情況各會出現4次，并且重疊部分的面積都是正方形面積的四分之一，多次出現重疊部分圖形不規則的情況。到此，筆者給予了肯定，然后引導學生思考是否可以從規則圖形是正方形的四分之一找到解題的思路，是否可以將不規則圖形（圖4）轉化成如圖2或圖3的規則圖形。學生觀察圖4后，生回答：若將①號的三角形繞著O點逆時針旋轉90°，可以將重疊部分的圖形轉化成正方形。生：若將②號陰影部分繞著O點順時針旋轉90°，可以將重疊部分的圖形轉化成三角形，轉化后的重疊部分是大正方形的四分之一。筆者：對他們的做法，你們有什么疑問嗎？生：①號陰影部分為什么會與三角形OAB一樣呢？此時，生回答：圖形旋轉后大小不變。筆者：是的，圖形的旋轉不改大小，其實①號陰影部分三角形的邊OC和三角形OAB的OA是相等的，并且兩個三角形對應的內角也相等，所以它們是一樣的大小，這在以后初中會有更深入的學習。

本題不僅回顧了旋轉這一知識的難點，還滲透了讓學生應用圖形的變化來解決不規則圖形面積計算的問題，通過一步步引導使學生的思維走向深刻。

三、培養思維的廣闊性——看見知識間的聯系

復習課的內容知識具有系統性的特點，是引導學生歸納梳理知識點、發現知識間聯系、培養思維廣闊性的好時機。具體地在梳理階段，可以引導學生將學習過的知識放在一起進行比較，從而產生新的東西。

如“圖形的運動”的總復習，在引導學生復習完舊知識之后，筆者將四種運動的方式先以動態的方式展示，再讓學生比較觀察四種運動的共同點與不同點。通過尋找共同點，發現圖形運動的共性是形狀不發生變化，感受四種運動的內在聯系。

【教學片段】

筆者通過多媒體展示一個直角三角形，再以高為中心進行旋轉，形成一個圓錐。

師：讓我們帶著運動的眼光看圓錐和圓柱，你能看到哪些圖形的運動呢？

生：圓錐可以由三角形旋轉的軌跡形成。

師：同學們的觀察很仔細，那圓柱可以通過什么圖形的運動來得到嗎？

生：通過固定長方形的一條長或寬，然后進行旋轉，旋轉軌跡就是圓柱。

生：圓柱還可能是圓形上下平移的軌跡。

師：那長方體呢？

生：上下平移長方形的軌跡形成的。

生：也可以前后平移長方形。

師：那長方體除了可以由它的六個面平移得到，還有可能是什么方法呢？

生：可以是線段，線段平移變成了長方形，長方形再平移。

生：那線也可以是通過點的平移得到的。

生：那長方體也可以說是一個點經過平移得到的。

師：長方體居然是通過一個點運動得來的。同學們有沒有發現，移動點可以變成線，移動線可以成面，移動面可以成體。學了圖形的運動，我們就能用運動的眼光來觀察事物。

可以發現，通過觀察立體圖形，尋找圖形的運動，不僅調動學生利用本節課復習的內容來解決問題，還培養學生的觀察力與空間想象力。

（作者單位：福建省連江縣東湖中心小學 責任編輯：王振輝）