基于層次多尺度散布熵的滾動軸承智能故障診斷

鄢小安，賈民平

（1.南京林業大學機械電子工程學院，南京 210037； 2.東南大學機械工程學院，南京 211189）

0 引 言

滾動軸承作為機械設備重要的組成部件，在航空航天、高速鐵路、礦山冶金、風力發電等行業都是必不可少的[1]。在實際工程應用中，隨著機械設備的長期運轉，受載荷、轉速、環境等多因素影響，軸承會不可避免地出現損壞，其故障發展過程通常會經歷正常、輕微故障、中度故障、嚴重故障、失效等幾個階段。然而，滾動軸承在整個生命周期內的運行健康狀態不易有效辨識和區分。因此，如何采用先進的特征提取方法從軸承全壽命周期數據內獲取有效豐富的故障診斷信息，對保障機械設備安全穩定運行具有重要的現實意義[2]。

近些年，研究學者提出許多非線性動力學方法用于評估信號的復雜性與不確定性，如譜熵、樣本熵、排列熵[3]、模糊熵、符號動力學熵[4]等。以上方法在機械故障診斷領域得到了很好的應用。孫鮮明等[5]提出一種瞬時包絡尺度譜熵，有效提取了軸承故障信息，并對軸承早期故障異常點進行了準確識別。馮輔周等[6]采用一種小波相關排列熵對軸承早期故障進行了有效識別。李永波等[7]提出一種層次模糊熵（Hierarchical Fuzzy Entropy, HFE）獲取軸承故障特征信息，并結合二叉樹支持向量機準確地識別了軸承不同故障類型及程度。Wu等[8]結合多尺度排列熵（Multiscale Permutation Entropy, MPE）和支持向量機有效地識別了軸承故障類型。Zhu等[9]采用層次樣本熵（Hierarchical Sample Entropy, HSE）提取軸承故障特征，并結合基于粒子群優化的支持向量機對軸承故障模式進行了有效辨識。Zheng等[10]將廣義復合多尺度排列熵（Generalized Composite Multiscale Permutation Entropy,GCMPE）與拉普拉斯分值特征選擇相結合對軸承故障模式進行了有效檢測。Wang等[11]首先采用一種廣義精細復合多尺度樣本熵（Generalized Refined Composite Multiscale Sample Entropy, GRCMSE）獲取軸承故障特征信息，然后將提取的故障特征輸入到支持向量機中進行了有效識別。然而，上述方法僅在原信號多尺度或多層次上挖掘軸承故障信息，沒有同時兼顧信號不同層次及不同頻段上的多尺度故障特征。換言之，上述方法所獲取的故障信息不夠全面、豐富。因此，為解決上述方法中存在的問題，Yang等[12]將層次多尺度排列熵（Hierarchical Multiscale Permutation Entropy, HMPE）和模糊支持張量機相結合，對不同的軸承故障類型進行了有效識別。另外，散布熵（Dispersion Entropy, DE）作為一種新的信號復雜性評價指標[13-15]，與現有的排列熵（Permutation Entropy, PE）、模糊熵（Fuzzy Entropy, FE）和樣本熵（Sample Entropy, SE）相比，具有運行速度快、計算效率高的優點。當時間序列的數據長度較小時，散布熵不會出現沒有定義的熵值，并且很好地考慮到了信號幅值的重要信息。因此，在散布熵優點的基礎上，Zhou等[16]提出了一種修改的層次多尺度散布熵（Modified Hierarchical Multiscale Dispersion Entropy, MHMDE），并結合核極限學習機對旋轉機械關鍵部件（如軸承、齒輪）進行了有效的故障識別。然而，文獻[12]和[16]的方法是依靠人為經驗選取熵值的重要參數，不具備自適應性，而且容易影響故障特征提取性能。

同時，在故障信息獲取后需要進行智能識別。為此，許多線性或非線性向量分類模型被依次提出，包括線性判別分析（Linear Discriminant Analysis, LDA）、人工神經網絡（Artificial Neural Network, ANN）、極限學習機（Extreme Learning Machine, ELM）和支持向量機（Support Vector Machine, SVM）等，其中SVM因其算法簡單、魯棒性好在智能診斷領域受到了極大關注。然而，SVM在應用過程中需要將矩陣形式的特征信息轉換成向量形式，這容易引起原振動信號內部結構信息丟失，從而降低分類性能。因此，為克服這一問題，Luo等[17]在2015年提出一種新型非線性分類模型——支持矩陣機（Support Matrix Machine, SMM）。與傳統SVM相比，SMM可以直接從原始特征矩陣中學習其內部結構信息，具有更強的小樣本特征學習性能和魯棒性。迄今為止，SMM已成功應用在腦電圖分類中，但其在軸承健康狀態識別中的應用報道較少。

綜上，本文結合層次分解、多尺度粗粒化分析和鳥群優化算法提出一種基于層次多尺度散布熵（Hierarchical Multiscale Dispersion Entropy, HMDE）的軸承智能診斷方法。采用參數自適應優化的HMDE提取矩陣形式的軸承故障特征信息，將提取的多維故障特征矩陣輸入SMM進行模型訓練并完成軸承健康狀態的自動識別。通過兩組軸承加速壽命實驗數據的分析，以驗證提出方法在識別軸承故障模式與故障程度方面的有效性。

1 層次多尺度散布熵

1.1 HMDE的定義

圖1為HMDE的流程圖。對于一個給定的時間序列{x(i),i= 1 ,2,… ,N}，HMDE的計算過程如下：

1）定義一個平均算子Q0和差分算子Q1為[18]

式中 2n-1為算子的長度，n為正整數，Q0(x)和Q1(x)分別表示原始時間序列在第一層分解中的低頻成分和高頻成分。

2）為了描述信號的層次分析，當j=0或1時，定義第k層算子的矩陣形式為[19]

3）為了獲得層次分解過程中各層的層次分量Xk,e，需要反復使用上述定義的Qkj算子，同時需要定義一個一維向量[γ1,γ2,… ,γk]和一個整數值，其中{γp,p= 1 ,2,… ,k} ? { 0,1}表示第p層的平均或差分算子。據此，第k層的第e個節點的層次分量可表示為[20]

4）根據公式（5）計算各層次分量Xk,e在τ尺度下的復合粗粒化序列

式中DE(·)為散布熵運算，m為嵌入維數，c為類別個數，d為時間延遲（s），k為分解層數，e為節點，τ為尺度因子。

1.2 參數影響研究

為了考察不同參數對HMDE性能的影響，對美國凱斯西儲大學（Case Western Reserve University, CWRU）公開的基準數據集[21]進行分析。試驗裝置由驅動電機、軸承座、轉矩傳感器和測力計等組成，如圖2所示，驅動端軸承為 SKF6205，風扇端軸承為 SKF6203。試驗過程中，采樣頻率為12 kHz，采樣長度為4 096點，在電機驅動端軸承座上安裝一個加速度傳感器分別采集 1組軸承正常加速度數據和1組軸承外圈故障數據。限于篇幅，表1僅列出了不同參數下軸承正常信號的前2行4列的層次多尺度散布熵。

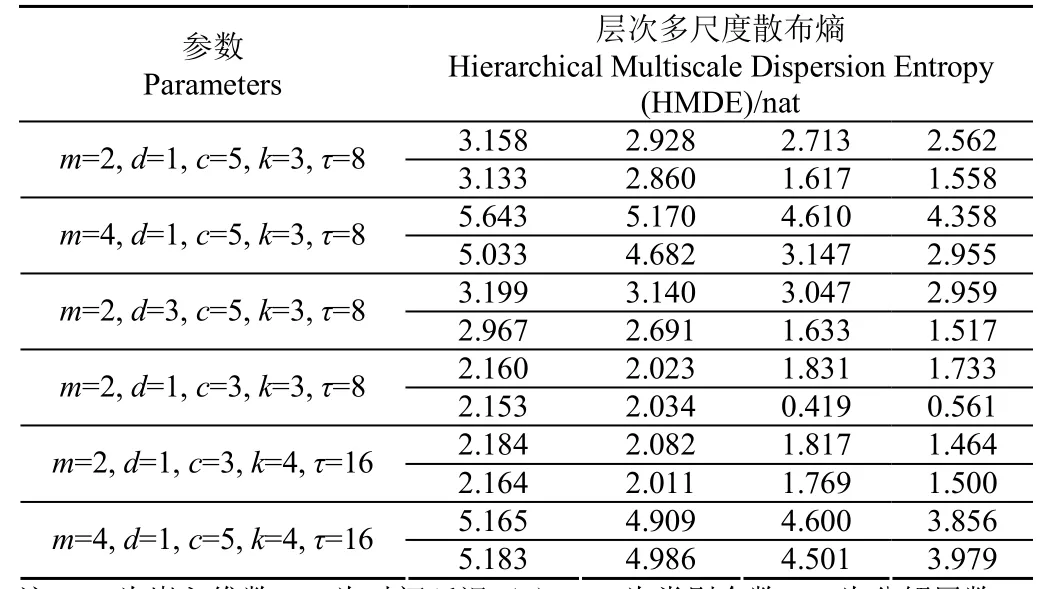
表1 不同參數下軸承正常信號的層次多尺度散布熵Table 1 HMDE of bearing normal signal under different parameters

從表1可以看出，當其他參數固定、嵌入維數m增加時，各層次或尺度下的散布熵值會出現一定增長。當其他參數固定、時間延遲d增加時，各層次或尺度下的散布熵值也會出現變化，但變化程度不明顯。當其他參數固定、類別個數c增加時，各層次或尺度下的散布熵值會發生較明顯變化。此外，當其他參數固定、分解層數k和尺度因子τ增加時，可以獲取更豐富、全面的散布熵特征，但也增加了相應的計算量。由于外圈故障信號的HMDE的變化規律與表1基本一致，這里不再重復贅述。因此，通過上述分析可以得出，時間延遲d對HMDE的計算結果影響較小，而其他4個參數（即嵌入維數m、類別個數c、分解層數k和尺度因子τ）對計算結果具有較大影響。

為了分析HMDE對軸承故障特征提取的有效性，將其與現有的7種復雜性度量方法進行對比分析。這7種對比方法分別為精細復合多尺度散布熵（Refined Composite Multiscale Dispersion Entropy, RCMDE）[22]、GCMPE、GRCMSE、HFE、HSE、MHMDE和HMPE。具體地，分別采用HMDE和7種對比方法計算上述軸承正常數據和外圈故障數據的熵值變化情況，并計算兩者之間的歐式距離（Euclidean Distance, ED），進而對比不同方法的軸承故障特征提取性能。需要注意的是，各算法中的參數均設置為嵌入維數m=3，時間延遲d=1 s，類別個數c=5，尺度因子τ=8，分解層數k=3，相似容限r=0.15σ，其中σ為原信號的標準差。限于篇幅，表2僅列出了不同方法下軸承正常信號的前1行4列的熵值。表3列出了各算法5次試驗的平均歐式距離ED和平均運行時間。從表3可看出，相比其他方法，HMDE的平均歐式距離最大，說明HMDE獲得的特征信息更具區分性，具備更優越的信號復雜性評估性能。此外，就各算法的平均運行速度而言，HMDE的運行時間與MHMDE比較接近，同時明顯小于GRCMSE、HFE、HSE和HMPE的運行時間，但大于RCMDE和GCMPE的運行時間，這主要是由于 HMDE中集成了層次分解和多尺度分析過程，因此引起了計算效率的下降。

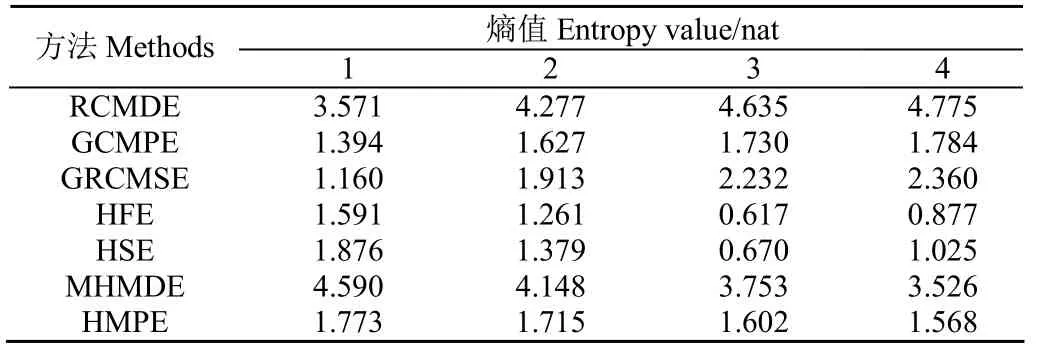
表2 不同方法下軸承正常信號的熵值Table 2 Entropy value of bearing normal signal with different methods

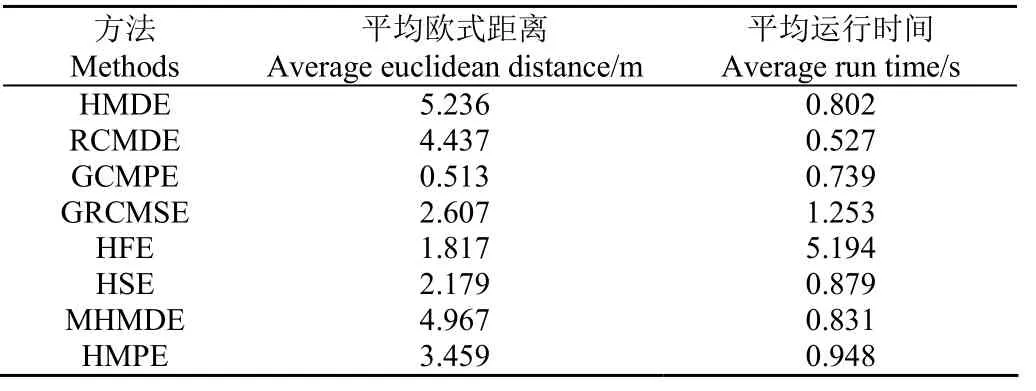
表3 不同方法的平均歐式距離和平均運行時間Table 3 Average Euclidean distance and average run time of different methods

1.3 參數優化

目前，群智能尋優算法在解決參數優化問題方面卓有成效，包括常見的粒子群優化（Particle Swarm Optimization, PSO）、蟻群算法（Ant Colony Algorithm,ACO）、蝙蝠算法（Bat Algorithm, BA）等。鳥群優化算法（Bird Swarm Algorithm, BSA）是Meng等[23]在2016年提出的一種新型仿生尋優算法。與其他尋優算法相比，BSA在參數優化方面具有優化精度高、穩定性強、收斂速度快等優點。為此，綜合考慮各參數之間的交互作用，本文采用BSA對HMDE的4個重要參數（即嵌入維數m、類別個數c、分解層數k和尺度因子τ）進行自適應選取。參數優化過程概括如下：

1）初始化種群和設置 BSA的各項參數。當迭代數t=0時，設置鳥群規模N=20，最大迭代數M=30，初始化飛行頻率FQ，覓食頻率P和幾個常量（即認知加速系數C，社會加速系數S，0～2之間的正整數FL、正數a1和正數a2)。

2）計算適應度值。根據式（7）所示的適應度函數計算并比較鳥群的適應度值，確定鳥群個體最佳位置和鳥群整體最佳位置。

式中xi為錯誤分類樣本數，xc為正確分類樣本數，fitness(i)為第i只鳥的當前適應度值。當fitness(i)取到最大值時，對應的鳥群個體最佳位置為pi,j，同時對應的鳥群整體最佳位置為gj。

3）通過判斷飛行頻率FQ與迭代數t相乘再除以100的運算t×FQ/100是否存在余數，執行迭代運算并確定位置更新公式。具體如下：

若t×FQ/100存在余數，則隨機生成一個均勻分布數。當隨機數小于覓食頻率P時，鳥群個體將執行覓食行為，位置更新公式如式（8）；當隨機數大于或等于覓食頻率P時，鳥群個體保持警戒行為，位置更新公式如式（9）。

式中rand(0,1)為0到1之間的一個均勻分布隨機數。

若t×FQ/100不存在余數，當鳥群個體為生產者時，位置更新公式如式（10）；當鳥群個體為乞討者時，位置更新公式如（11）。

式中 randn是一種產生隨機數或矩陣的函數，randn(0,1)表示生成均值為 0、標準差為 1的高斯分布隨機數，k?[1,2,3,… ,N],k≠i。

4）根據步驟3）的準則，更新每個鳥群個體的位置。若當前鳥群個體位置好于先前鳥群個體位置，則當前鳥群個體位置被當作最優位置。否則，保留先前鳥群個體位置為最優位置繼續鳥群更新。

5）判斷是否滿足停止條件。若達到最大迭代次數或最小錯分率，則整個優化過程結束，輸出鳥群的最優位置（即HMDE的最優組合參數）。否則，繼續循環迭代直到滿足停止條件。

2 基于HMDE的軸承智能診斷方法

為了獲取更豐富、更全面的軸承故障特征信息，同時提高故障診斷精度，本文提出一種基于HMDE的軸承智能故障診斷方法。圖3為提出方法的流程圖，其具體實現過程表述如下：

1）通過在試驗設備上安裝加速度傳感器，獲取全壽命周期內的軸承振動數據。

2）通過鳥群優化算法自適應確定 HMDE的最優參數，并根據最優參數計算不同健康狀態下軸承振動數據的HMDE作為多維度特征矩陣。

3）將多維度特征矩陣隨機劃分為訓練樣本矩陣和測試樣本矩陣，采用訓練樣本矩陣對SMM進行模型訓練，并將測試樣本矩陣輸入到訓練好的 SMM 模型中進行測試和自動輸出識別結果。在該步驟中，假設給定的訓練數據集為為第i個輸入矩陣，yi? { 1,-1 }為訓練標簽，d1和d2分別表示輸入矩陣的行數和列數，則SMM可以通過合頁損失函數和譜彈性網絡懲罰函數來實現模型的訓練和分類，如下所示：

3 試驗驗證

本文通過軸承故障診斷試驗來驗證所提方法的故障特征提取與智能診斷能力。試驗采用 2組軸承加速壽命數據集：西安交通大學與昇陽科技的XJTU-SY軸承加速壽命試驗數據[24]、東南大學狀態監測與故障診斷研究中心的ABLT-1A軸承加速壽命試驗數據。

3.1 設備與方法

XJTU-SY軸承加速壽命試驗數據源自西安交通大學與浙江長興昇陽科技有限公司的機械裝備健康監測聯合實驗室。圖4所示試驗臺主要由數字式力顯示器、電機轉速控制器、交流電機、支撐軸承和液壓加載系統等部分組成。在試驗過程中，將2個PCB-352C33加速度計分別安裝在測試軸承的垂直和水平方向，采用DT9837便攜式動態信號采集器對軸承全壽命數據進行了監測與記錄。測試軸承型號為UER204，滾動體直徑為7.92 mm，節圓直徑為34.55 mm，滾動體數量為8個，接觸角為0°。數據采集過程中，電機轉速設置2 400 r/min，軸承承受的徑向力10 kN，采樣頻率25.6 kHz，采樣間隔1 min，每次采樣時長1.28 s。在軸承加速壽命試驗結束后，軸承3_1表面出現了外圈故障，而軸承3_4存在內圈故障，如圖4所示。因此，本文采用軸承3_1和軸承3_4的全壽命周期數據進行分析。

ABLT-1A軸承加速壽命試驗數據源自東南大學機械工程學院的狀態監測與故障診斷研究中心。圖5所示的試驗臺主要由軸承測試模塊、傳動系統、加載系統、潤滑系統、電氣控制系統、計算機監控系統等部分組成。在實驗過程中，軸承測試模塊裝有4個軸承，軸承型號為HRB6308，滾動體直徑為15.081 mm，節圓直徑為65.5 mm，滾動體數量為8個，接觸角為0°。為了加速軸承的性能退化，在徑向加載油缸內安裝徑向大活塞，采用徑向大活塞對測試軸承進行徑向加載。具體地，通過加載系統在設備運行過程中定期添加一定質量的砝碼，使得每個軸承受到一個近15 kN的徑向載荷。此外，測試過程中，電機轉速平均穩定在3 000 r/min，采樣頻率設定為25.6 kHz，3個PCB加速度計以垂直方向安裝在軸承座上對整個軸承全壽命數據進行測量，并通過NI9234數據采集卡和搭建的LabVIEW監測軟件，每隔15 s采集并保存1組軸承振動加速度數據。當測試軸承在負載下連續運行10 h后，由于振動均方根超出了預定閾值，試驗設備發生停機。通過線切割技術將 4個軸承切開，明顯發現軸承 2的滾動體表面出現局部剝落故障，如圖5所示。因此，本文采用軸承2的全壽命周期數據進行分析。

在實際中，軸承故障程度的識別要比軸承故障類型的識別更加困難。目前，對于軸承全壽命過程，沒有明確的準則被用于確定和劃分軸承性能退化階段，即全壽命過程中軸承故障程度是不易辨識的。為解決這一問題，現有許多研究學者通過根據一些指標（如峭度、均方根、能量或信息熵）對軸承性能退化階段進行大致劃分，從而獲取不同故障程度的軸承振動數據，并采用基于熵值理論的特征提取及診斷方法，實現不同軸承故障程度的識別。因此，基于前人研究，為了實現軸承故障模式及程度的有效識別，本文首先選用均方根指標對 2組試驗的整個軸承性能退化數據進行劃分，獲取不同故障程度的軸承振動數據。然后，采用參數優化的HMDE提取軸承故障特征信息，并結合支持矩陣機進行軸承故障程度識別。

3.2 結果與分析

首先，采用均方根指標對 2組軸承加速壽命試驗數據（XJTU-SY和ABLT-1A）進行劃分，獲取不同軸承狀態數據。表4列出了不同軸承狀態數據的詳細信息，包括每種軸承狀態的樣本數及其對應的均方根。如表4所示，對于XJTU-SY軸承數據集，將軸承3_1全壽命數據中第525、2 350、2 475和2 538 min對應的4組數據作為 4種軸承狀態（即正常、外圈輕微故障、外圈中度故障、外圈嚴重故障），同時將軸承3_4全壽命數據中第1 417、1 445和1 479 min對應的3組數據作為其他3種軸承狀態（即內圈輕度故障、內圈中度故障和內圈嚴重故障），共7種軸承狀態，每種軸承狀態具有50個樣本，每個樣本包含2 048個數據點，隨機選取每種軸承狀態的25個樣本作為訓練，剩余樣本作為測試，即訓練集和測試集都包含7×25=175個樣本。對于ABLT-1A軸承數據集，將軸承2全壽命數據中第85、280、291和292 min對應的4組數據作為4種軸承狀態（即正常、滾動體輕微故障、滾動體中度故障、滾動體嚴重故障），每種軸承狀態具有60個樣本，隨機選取每種軸承狀態的30個樣本作為訓練，剩余樣本作為測試，即訓練集和測試集都包含4×30=120個樣本。值得說明的是，在2組試驗中，每種軸承狀態的樣本均是通過數據分割方法[25]（即采用一個滑移窗）得到的。限于篇幅，圖6僅繪制了不同的外圈軸承振動信號的時域波形和包絡譜。圖7為不同狀態下滾動體振動信號的時域波形和包絡譜。如圖6和圖7所示，隨著軸承外圈故障或滾動體故障程度的加深，包絡譜中軸承外圈故障特征頻率fo=123.32 Hz或滾動體故障特征頻率fb=102.8 Hz處的幅值越來越明顯，這與實際軸承故障演化規律相符合。

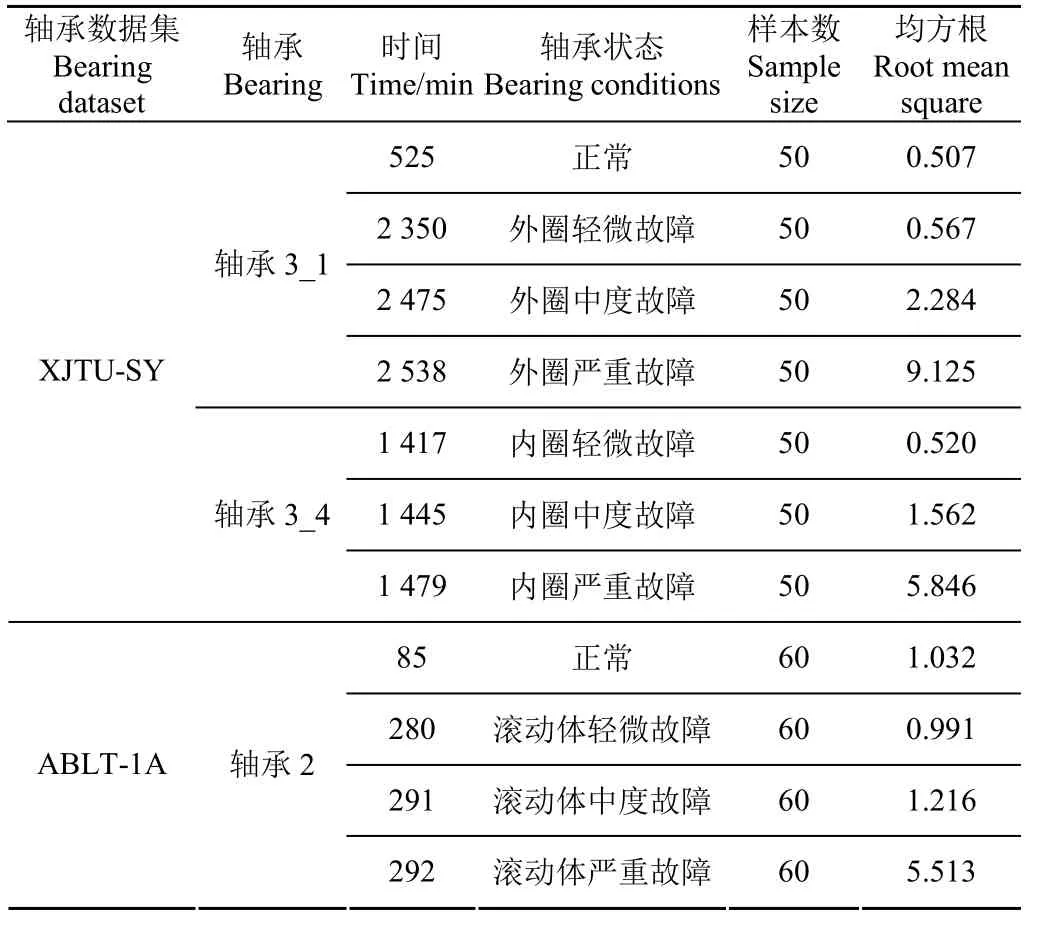
表4 不同軸承狀態數據Table 4 Data of different bearing conditions

然后，采用本文方法進行軸承故障特征提取和智能診斷。限于篇幅，圖8僅顯示了本文方法對XJTU-SY軸承數據集獲得的混淆矩陣。在混淆矩陣中，橫坐標序號1～7分別表示預測的7種軸承狀態，縱坐標序號1～7分別表示實際的 7種軸承狀態（即正常、外圈輕微故障、外圈中度故障、外圈嚴重故障、內圈輕度故障、內圈中度故障和內圈嚴重故障）。混淆矩陣中的對角線數值表示不同軸承狀態對應的識別精度。從圖8可以看出，6種軸承狀態（即正常、外圈輕微故障、外圈中度故障、外圈嚴重故障、內圈輕度故障、內圈中度故障）的識別精度都是100%（即混淆矩陣對角線前6個數值均為1），而第 7類軸承狀態（內圈嚴重故障）的一個樣本被錯誤分為第 1類軸承狀態（正常），其識別精度僅有 96%（24/25），相當于 0.96。因此，在測試集中，本文方法正確識別了174個數據樣本，僅有1個數據樣本被誤分。也就是說，本文方法取得了99.43%（174/175）的識別精度，驗證了本文方法在識別不同軸承狀態中的有效性。

最后，為了突出本文方法的優勢，將本文方法與 7種同類型診斷方法（即RCMDE、GCMPE、GRCMSE、HFE、HSE、MHMDE和HMPE）進行對比分析。為了避免診斷結果的偶然性，每種算法都進行5次試驗。此外，為了確保算法對比的公平性，7種對比算法的重要參數均通過鳥群優化算法進行自適應選取，各參數優化結果如表5所示。值得注意的是，由于 RCMDE、GCMPE、GRCMSE、HFE和HSE算法對于每個樣本提取的特征信息屬于向量形式，因此，這 5種對比算法的分類過程都通過SVM來完成，且各分類模型參數均采用默認值（即懲罰參數C1=1，核參數λ=1/n），其中n為提取的故障特征維度。與提出方法一樣，MHMDE和HMPE的分類過程均采用SMM來完成。表6列出了不同方法5次試驗結果的平均識別精度準確率和標準差。從表6可看出，對于XJTU-SY軸承數據集，本文方法的平均識別精度為99.66%，標準差為 0.312。與 RCMDE、GCMPE、GRCMSE、HFE、HSE、MHMDE和HMPE相比，本文方法的標準差更小（即算法穩定性更好），平均識別精度分別提高了3.89、12.34、6.63、9.15、7.09、0.81和2.63個百分點。對于ABLT-1A軸承數據集，本文方法的平均識別精度為99.34%，標準差為0.371。與7種對比方法（即RCMDE、GCMPE、GRCMSE、HFE、HSE、MHMDE和HMPE）相比，本文方法的平均識別精度分別提高了2.17、3.51、6.17、9.51、11.51、1.17和 3.01個百分點。由此可知，相比傳統的基于多尺度熵或層次熵的智能故障診斷方法，本文方法在識別滾動體故障程度方面具有一定優越性。需要說明的是，目前存在許多其他的先進分類模型，如非并行最小二乘支持矩陣機[26]、卷積神經網絡[27]、自編碼器[28]。因此，在將來的工作中，本文方法中的分類過程可以采用這些先進的分類模型替代 SMM 進行軸承故障類型識別。

表5 不同對比方法的參數設置Table 5 Parameter settings for different contrast methods

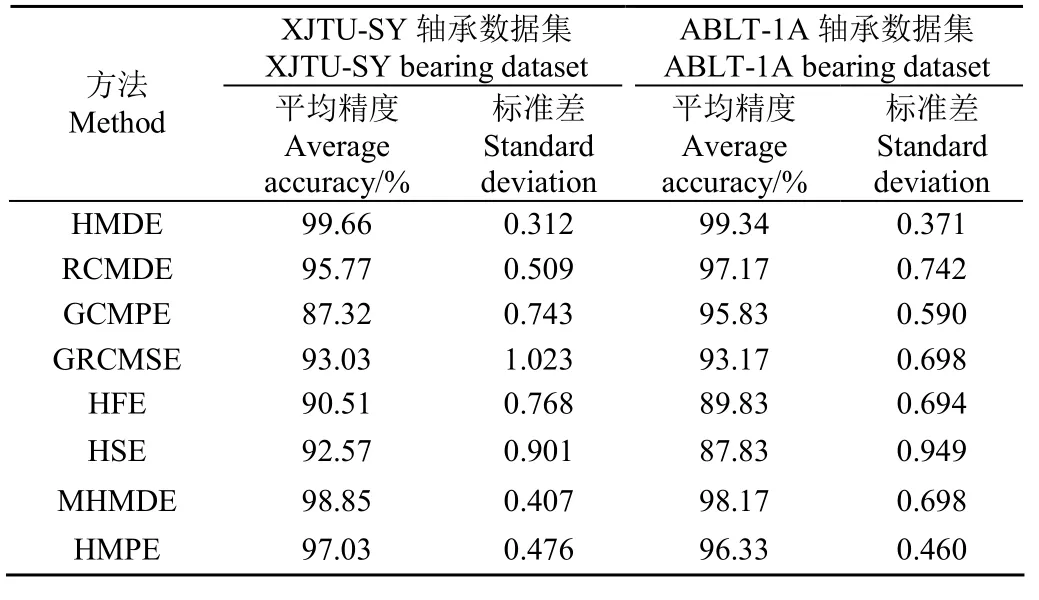
表6 不同診斷方法的對比結果Table 6 Comparison results of different diagnosis methods

4 結 論

1）針對全壽命周期內滾動軸承故障模式與程度難以有效識別的問題，提出了一種基于層次多尺度散布熵的滾動軸承智能診斷方法。該方法采用了BSA算法自適應優化HMDE的重要參數，避免了HMDE在特征提取過程中因人工選取參數而影響診斷效果的問題，同時兼顧了SMM在處理多維特征矩陣方面的優點。

2）通過試驗分析對本文方法在軸承故障模式與故障程度識別中的有效性進行了驗證。試驗結果表明：對于第1和第2組試驗，本文方法的平均識別精度可分別達到99.66%和99.34%。相比RCMDE、GCMPE、GRCMSE、HFE、HSE、MHMDE和 HMPE方法，本文方法在第 1組試驗中的平均識別精度分別提高了3.89、12.34、6.63、9.15、7.09、0.81和2.63個百分點。本文方法在第2組試驗中的平均識別精度分別提高了2.17、3.51、6.17、9.51、11.51、1.17和3.01個百分點。