基于傅里葉描述子和共振頻率的不規則果形梨果硬度評估指標構建

王 鵬 ，吳 杰 ,2※

（1.石河子大學機械電氣工程學院，石河子 832000；2.綠洲特色經濟作物生產機械化教育部工程研究中心，石河子 832003）

0 引 言

果蔬硬度是其重要的內部品質之一，硬度與果蔬的口感、成熟度等密切相關，是梨果品質檢測重要指標。國內外學者研究發現共振頻率是評估硬度變化的重要參數。通常果蔬硬度采用頻率指標f2m2/3（f為赤道部感測頻率，m為質量）評價[1]，但已有研究表明，果形對果蔬共振頻率有影響，Chen等[2]研究指出，評價指標f2m2/3適于近球形果蔬的硬度評價，但對非球形果蔬硬度評價誤差較大。為此，Cherng等[3]提出了一種適于評價橢球形果蔬硬度的雙頻指標SCherng=()2/3m2/3ρ1/3（f1為赤道部感測頻率，f2為萼端或梗端感測頻率，ρ為果蔬密度），筆者團隊針對多為卵圓形的庫爾勒香梨，從香梨赤道部和萼端分別感測共振頻率f1和f2，構建了一種雙頻硬度指標Sf1f2= ( 0.4f1+ 0.6f2)2m2/3，提高了香梨硬度評價性能[4]。盡管如此，梨果種類豐富，果形復雜，其中啤梨為典型的果形不規則梨果，現有的各種基于規則果形構建的頻率指標，可能都不適于啤梨硬度的精確評價。因此，有必要基于共振頻率構建一種適于評價果形不規則梨果硬度的指標。

針對復雜果形果蔬，了解果形對共振頻率的影響規律，是構建消除果形影響的新硬度評價指標的關鍵。大多研究采用縱橫比、圓度比、圓形度、偏心度、離心率等描述果形[5-9]，李凡等[5]采用縱橫比和圓度比對香梨形狀定量描述獲得5種果形，申翠香等[7]采用圓形度描述蘋果果形。這些描述方法多用于蘋果、桃子、柑橘等“比較端正”果形的描述[8-11]，但卻很難全面描述果形復雜不規則的梨果。近年來，郝敏等[12]采用具有平移伸縮和旋轉不變性且有多特征描述能力的Zernike矩描述馬鈴薯，但Zernike矩描述果形時，數據處理量大，計算耗時長[13]。傅立葉描述子具有很強的果蔬外形重建功能且對復雜果形有較強的描述能力[14-16]，這一方法在描述木瓜、畸形馬鈴薯、楊桃等果蔬外形輪廓時，能夠兼顧全局及局部特征[17-19]，其中 Limsiroratana等[17]研究木瓜果形描述方法時，發現傅里葉描述子計算快速且抗噪性強；EIMasry等[18]采用傅里葉描述子描述畸形馬鈴薯，并選取4個傅里葉描述子識別畸形馬鈴薯，識別率可達 96.2%；Abdullah等[19]采用傅里葉描述子描述楊桃外形，對3種變形果的識別率最高可達 100%。上述研究表明傅里葉描述子可以描述果形復雜多變的果蔬外形特征。

因此，本文采用傅里葉描述子對啤梨果形進行定量描述，并結合試驗模態和有限元模態分析方法，了解啤梨果形變化對其頻率的影響規律，構建適于不規則果形的梨果硬度準確評價指標，為復雜果形梨果硬度振動法無損檢測提供研究基礎。

1 材料與方法

1.1 啤梨試樣

啤梨試樣于2019年10月于石河子水果批發市場采購，剔除損傷及病蟲害試樣，立即貯藏于?2～0 ℃、相對濕度85%～95%的冷庫備用。試驗前將試樣在(23±1)℃室溫下回溫24 h。

1.2 研究思路

首先結合試驗模態和有限元模態分析結果確定啤梨試樣適宜的振型和對應的模態頻率，采用傅里葉描述子和縱橫比描述啤梨試樣果形；然后利用Pearson線性相關性分析果形對啤梨振動頻率的影響規律，進而構建含有果形描述子和共振頻率的新硬度評估指標以消除果形對硬度評估的影響；最后結合M-T穿刺硬度實測值，采用普通最小二乘法（ordinary least square, OLS）分別對基于頻率的無損硬度與M-T穿刺硬度SMT進行線性回歸分析。研究方案流程如圖1所示。

1.3 啤梨試驗模態分析

試驗模態分析系統如圖2所示，選擇單點感測多點激勵方式采集振動信號構建頻率響應函數[4]，啤梨試樣用橡皮筋懸掛使其處于接近自由振動狀態。根據前期試驗在試樣表面均布56個點，取赤道部的32號點（見圖3）為感測點，LC1305型力錘（河北朗斯有限責任公司）以9～12 N的力從1號點依次開始敲擊各點[4]，固結在感測點的LC0408T型加速度傳感器（河北朗斯有限責任公司）感測信號，隨機選取10個試樣進行試驗模態分析。

1.4 啤梨有限元模態分析

如圖4所示，采用Rigelscan Elite型三維掃描儀（精度0.0185 mm，武漢中觀自動化科技有限公司）獲得啤梨試樣.asc格式點云模型，然后將其導入正逆向混合設計軟件Geomagic Wrap 2017（美國，Geomagic公司）進行逆向處理，獲得.stp格式實體模型，最后將實體模型導入有限元分析軟件Abaqus 2017（法國，達索SIMULIA公司）中進行有限元分析。

采用有限元軟件Abaqus 2017（法國，達索SIMULIA公司）劃分網格時，由于啤梨試樣小且形狀不規則，因此選用10節點二次四面體結構實體單元C3D10進行自由網格劃分，避免大量分割操作導致工作量增加和人為誤差。為減少計算時間，在保證精度的前提下將網格大小設定為2 mm。假設啤梨為均質、各向同性的線彈性體，模型泊松比取0.3[20]，采用排水法測得啤梨密度。采用有限元分析軟件 Abaqus進行啤梨有限元模態分析時，在Frequency分析步中選擇子空間迭代算法（subspace）求解器，求解運動方程+Ka(t) = 0（M為質量矩陣，為加速度矢量，K為剛度矩陣，a(t)為速度矢量），設置最大頻率為1 000 Hz，頻移為100 Hz，特征值提取數量為20，每次循環矢量數為28次，最大循環次數為30次，獲得啤梨前20階模態振型和對應的固有頻率進行分析。

1.5 啤梨固有頻率歸一化

由于質量對模態固有頻率影響很大[21-22]，采用模態分析啤梨果形對頻率影響時，用式（1）對各階模態固有頻率進行歸一化處理以消除質量對固有頻率的影響[20]：

式中m為試樣質量，kg；m0為常數，根據前期試驗取0.1 kg；f為某一階模態固有頻率，Hz；fn為歸一化的固有頻率，Hz。

1.6 啤梨果形描述方法

1.6.1 果形輪廓的提取

采用EOS 750D型佳能數碼相機（日本，佳能有限公司）采集啤梨圖像，采用Matlab 2014（美國，MathWorks公司）軟件中圖像處理工具箱對啤梨圖像進行灰度變換、閾值分割、邊界提取，獲得試樣外形輪廓，如圖5所示。

1.6.2 試樣輪廓半徑序列的計算

如圖6，計算試樣輪廓曲線的形心坐標x0和y0[23]：

式中n為試樣邊界輪廓曲線上的總樣點數；k為邊界輪廓曲線上點的序數。求得形心坐標x0和y0后，以形心坐標為圓心，果梗與果體交界處P1點作為起始點，按逆時針方向求半徑序列r(k)：

1.6.3 半徑序列的傅里葉變換

為避免試樣大小對果形分析的影響，將半徑序列r(k)歸一化處理[24]：

式中rav為試樣的平均半徑，Pixels；n為試樣邊界輪廓的樣點數，rg(k)為歸一化半徑序列。對歸一化半徑序列rg(k)進行離散傅里葉變換：

式中Fh為傅里葉描述子，h為傅里葉變換后的自變量，2π/n為相鄰兩樣點間夾角，Fh可理解為半徑序列變化h次的程度[23]。當h=0時，F0表征試樣平均半徑信息，F1表征試樣外形的彎曲程度信息，F2表征試樣外形的伸長度信息，F3表征試樣外形的三角度信息，F4表征試樣外形的方形度信息[24]。

1.6.4 縱橫比q的計算

采用縱橫比描述啤梨果形時，測量如圖7所示啤梨試樣肩高的最大值Hmax(mm)和最小值Mmin(mm)以及赤道部最大直徑Dmax(mm)和最小直徑Dmin(mm)，縱橫比q由公式（9）計算求得[4]。

1.7 啤梨硬度的M-T穿刺法測定

采用TA.XP plus質構儀（英國，Stable Micro System公司）在啤梨梗端、赤道部和萼端 3個區域內每個區域隨機選取4個點進行帶皮M-T穿刺試驗[25-26]。采用直徑5 mm 的圓柱探頭，穿刺速度為 1 mm/s，穿刺深度為8 mm。穿刺硬度由穿刺前曲線的斜率計算得出，然后取12次穿刺試驗平均值作為梨整體硬度。

1.8 硬度評估指標的評價方法

在室溫(23±1) ℃、相對濕度 20%環境下，隨機選取140個啤梨試樣等分為7組，每2 d進行一次測試試驗。試驗時隨機選取一組啤梨試樣，每個試樣在15 min內依次進行激振試驗、圖像采集和M-T穿刺試驗，獲得啤梨基于頻率的無損硬度和M-T穿刺硬度。

采用普通最小二乘法（Ordinary Least Square, OLS）分別對基于頻率的無損硬度與M-T穿刺硬度SMT（N/mm）進行線性回歸分析[26]，回歸方程為

式中SZ為各頻率指標中的某一個；α和β分別為回歸方程的回歸系數和截距。

2 結果與分析

2.1 試驗模態對有限元模態的驗證

2.1.1 試驗模態與有限元模態的分析結果

瑞士有很多傳統的奶酪飲食，其中奶酪火鍋就是其中最著名的一款。如果說瑞士有什么美食的話，那一定首推奶酪火鍋。瑞士盛產奶酪，而且法令規定一個地區只能生產該地區產的奶酪，因此瑞士的奶酪直至今日仍能夠保持極其傳統的風味，且不同地區的奶酪味道各不相同。

通過啤梨試驗模態分析獲得 3個模態，分別為彎曲模態、擠壓模態和呼吸模態，如圖8所示。可以看到，彎曲模態在啤梨梗端發生較大變形，在萼端幾乎不發生振動變形；擠壓模態在赤道部發生最大變形，呼吸模態主要沿啤梨徑向發生擴張和收縮的振動變形。

啤梨進行有限元模態分析所獲得的20階有限元模態振型中，第1～6階頻率近似為0，為剛體模態；第16～20階振型變形復雜，為二階模態，本研究不予考慮。在第7～15階振型中，第8階與第7階變形相同，均為彎曲模態，第10階為擠壓模態，第13～15階模態變形相同，均為呼吸模態。

2.1.2 試驗模態與有限元模態頻率對比

調整有限元分析彈性模量值，當第 7階有限元彎曲模態頻率與試驗模態結果相同時，確定彈性模量值Eest，取這一彈性模量值為有限元模態分析的彈性模量并計算剩余各階有限元模態的固有頻率值[4]。計算有限元模態頻率與試驗模態頻率的差值，以差值絕對值與試驗模態頻率比值大小判別有限元模態分析的準確性。任取10個啤梨試樣進行試驗，結果如表1所示。頻率的有限元結果與試驗結果的相對誤差不超過3.25%,表明采用各向同質線彈性體的梨實體建模進行有限元模擬結果較準確，因此可以采用有限元模態分析果形對頻率的影響規律。

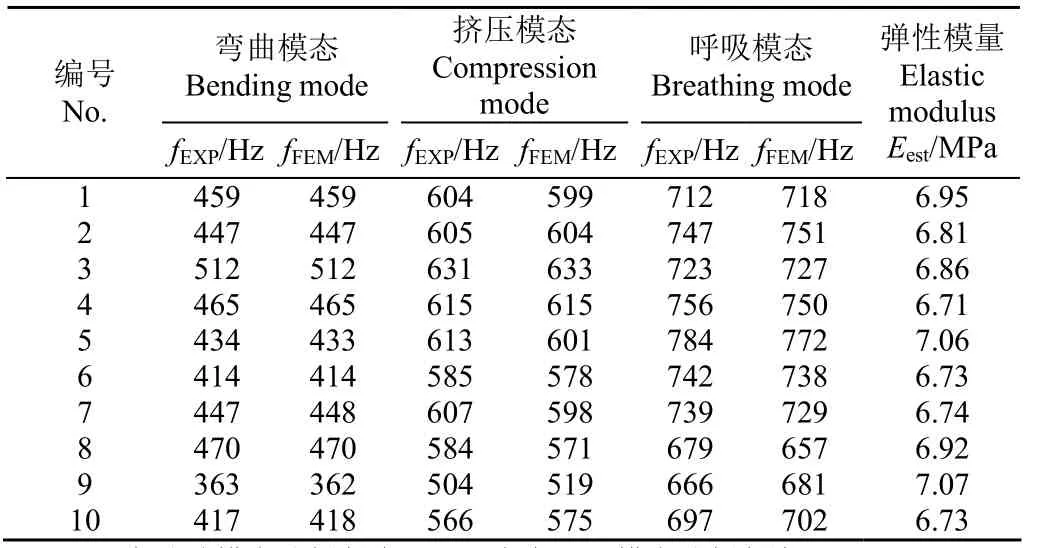
表1 試驗模態分析與有限元模態分析頻率比較Table 1 Comparisons between the experimental frequencies and the FEM frequencies

2.2 傅里葉描述子對啤梨外形描述結果分析

如圖9所示，前20個傅里葉描述子與F0的比值隨h增大迅速減小，但F4和F6與F0的比值出現反彈。當h大于16時，Fh與F0比值曲線趨于水平且比值小于0.005，即啤梨果形信息主要集中在前16個傅里葉描述子。

梨試樣輪廓和前10、15、20個傅里葉描述子反變換圖如圖10所示，采用前10個傅里葉描述子反變換獲得的梨輪廓圖基本能描述梨果形，但對啤梨梗端或萼端輪廓重合度較差；采用前15個傅里葉描述子反變換獲得的輪廓與原輪廓形狀度吻合度高。因此，盡管采用前20個傅里葉描述子反變換獲得的輪廓仍然與梨輪廓保持很好重合度，但采用前15個傅里葉描述子已足以描述啤梨試樣輪廓的主要信息。

2.3 果形對啤梨共振頻率的影響

對 100個啤梨進行有限元模態分析，本研究取彎曲模態、呼吸模態和擠壓模態的歸一化固有頻率進行分析。采用Pearson相關性分析方法對啤梨彎曲、呼吸和擠壓3種模態的歸一化固有頻率和前15個傅里葉描述子進行線性相關性分析，與歸一化固有頻率有較強相關性的 7個傅里葉描述子的相關系數如表2所示。

表2 歸一化固有頻率和傅里葉描述子間的相關性Table 2 Correlation between the normalized frequencies and the Fourier descriptors

由圖11可知，歸一化固有頻率fn與果形系數間關系可用下式表示

式中fn為歸一化固有頻率，S為果形描述子，a和b的取值由振型決定，各階振型對應a和b取值見圖11。

2.4 啤梨硬度評估指標的構建

果蔬硬度可用彈性模量E表征，且頻率f的平方與彈性模量E成正比[27-28]，故下式成立：

經轉換可得

將公式（1）和（11）代入公式（13），得

式中m0為常數，a、b值由圖11獲得，EFEM為有限元模擬彈性模量值，取2.1.2節計算Eest的平均值6.86 MPa，代入公式（14）中得到硬度評價指標SE：

圖12為啤梨在赤道部感測的振動頻譜曲線，共振頻率fBE為彎曲模態的頻率，其對應加速度幅值不突出試驗時不易提取。擠壓模態的共振頻率fC的加速度幅值很高，試驗時非常容易提取。因此，在應用新的硬度評價指標檢測啤梨時，評價指標中a、b分別取圖11中擠壓模態對應的值。

2.5 各頻率指標對啤梨硬度的評價能力比較

啤梨在室溫條件下硬度隨儲藏時間變化規律如圖13所示，由圖可知啤梨M-T穿刺硬度在12 d內總體呈現先快后慢的下降趨勢，M-T穿刺硬度在前6 d內急劇下降，6～12 d之間硬度下降速度減緩。

將縱橫比q和F1代入公式（15）獲得含有果形描述子的硬度指標SE(q)和SE（F1），由1.8節方法對基于頻率的硬度指標與M-T穿刺硬度SMT進行線性回歸分析，結果如圖14所示。傳統單頻硬度評估指標Sf與 M-T穿刺硬度SMT的決定系數較低（R2=0.733），啤梨試樣不規則果形可能是導致單頻指標Sf硬度評估值與M-T穿刺硬度實測值相關性不高的原因。

Cherng等[3]提出的雙頻硬度評價指標SCherng和筆者團隊研究提出的雙頻指標Sf1f2與 M-T穿刺硬度SMT的決定系數R2非常接近，分別為0.775和0.765，較傳統單頻硬度評估指標而言，與硬度實測值SMT相關系數有所提高，但由于這 2種硬度指標都只能消除近橢形果形對頻率的影響，相關系數提高效果并不顯著。采用新硬度指標SE評估啤梨硬度時，以縱橫比q和傅里葉描述子F1作為啤梨果形描述子分別帶入新指標SE計算獲得的指標SE(q)與M-T穿刺硬度SMT的決定系數R2值為0.746，指標SE（F1）與 M-T穿刺硬度SMT的決定系數R2值為 0.892，在各指標中最高。這表明傅里葉描述子能準確描述不規則果形梨果，本研究提出的硬度評價指標SE（F1）更適于復雜且不規則果形的啤梨硬度評估。

3 結 論

1）啤梨振動試驗模態分析獲得彎曲模態、擠壓模態和呼吸模態，彎曲模態和呼吸模態在赤道部振動變形較小，擠壓模態振動變形在赤道部變形較大，采用加速度傳感器在赤道部感測時更易于獲得擠壓模態的共振頻率。

2）采用前 15個傅里葉描述子足以描述啤梨外形特征，第1個傅里葉描述子F1與啤梨彎曲模態、擠壓模態和呼吸模態歸一化固有頻率高度線性相關，線性相關系數r分別為?0.923、?0.922、0.700，較適于描述啤梨復雜果形的變化。

3）基于擠壓模態的共振頻率（fC）和傅里葉描述子F1構建硬度指標SE(F1)，可消除果形對啤梨硬度評估的影響。與其他研究報道的頻率評估指標相比，該硬度指標檢測啤梨硬度值與M-T穿刺法檢測硬度值的決定系數R2為0.892，可用于果形復雜梨果硬度的較精確評估。