基于混合算法的光伏多峰值MPPT研究

郭昆麗，劉璐雨，蔡維正

(西安工程大學電子信息學院，陜西西安 710048)

光伏發電作為一種環保、無污染的發電方式受到了人們的關注，為了解決光伏發電系統能量轉換效率低[1]的問題，最大功率點跟蹤技術(maximum power point tracking，MPPT)是目前廣泛應用和研究的技術。然而在實際運用過程中，光伏陣列會被物體遮擋(如建筑物、灰塵覆蓋等)，形成局部遮陰情況，從而引起局部過熱。為了防止光伏陣列局部過熱現象，通常在光伏電池板處反并聯一個旁路二極管，但這會導致光伏陣列的輸出特性P-U 曲線，出現多個峰值，使得傳統的MPPT 算法失效[2]。

針對上述問題，文獻[3]提出基于粒子群優化算法來搜尋多峰值情況的最大功率點。雖然該方法能夠防止陷入局部最優點，但是單一的粒子群算法在粒子切換過程中會造成巨大的過沖和振鈴現象，對開關器件造成損壞。文獻[4]提出了采用人工神經網絡方法用于MPPT 技術，但是神經網絡的方法需要大量的歷史數據來訓練網絡。文獻[5]提出了一種基于電導增量法優化的粒子群全局MPPT 算法，將電導增量法同傳統粒子群算法結合起來對光伏陣列進行聯合控制。該方法的收斂速度比較慢，計算量比較大。文獻[6]提出了一種基于“遮陰度”模型的新型多峰全局最大功率點跟蹤重構算法，該方法對于復雜多變的遮陰現象，容易導致算法失效。文獻[7]提出了擾動觀察法結合模糊控制法，該方法在前期跟蹤過程中使用擾動觀察法，容易陷入局部最優值。

針對上述問題，本文提出了一種“兩步走”MPPT 技術。首先利用粒子群算法(PSO)和遺傳算法(GA)相結合的算法(PSO-GA)通過少量的迭代次數搜尋至最大功率點附近；然后切換至模糊控制方法來搜尋最大功率點，并穩定。這種混合算法彌補了單個算法的不足，提高了系統的速度和精度。通過粒子群算法和遺傳算法優缺點互補，避免陷入局部最優值和減少收斂時間。通過模糊控制方法可以使系統在最大功率點處穩定，避免振蕩帶來的能量損失。

1 光伏陣列的輸出特性

1.1 光伏陣列仿真模型

如圖1 所示，用Simulink 搭建了光伏陣列在不同輻照度下的仿真模型。為了防止局部過熱，在光伏電池處反并聯了一個二極管。本文給出1 000、800、600 W/m2三種輻照度進行模擬局部遮陰情況。將溫度設置為25 ℃，通過串聯的方式將光伏陣列進行連接。

圖1 光伏陣列局部遮陰仿真模型

1.2 光伏陣列輸出特性曲線

對圖1 中的光伏陣列模型進行仿真分析，得到輸出電壓、輸出電流、輸出功率的數據，進行繪圖，得到光伏陣列的輸出特性曲線，如圖2 所示。因為外部環境條件的不斷變化，所以P-U 曲線具有非線性特性。當溫度或輻照度發生變化時，最大功率點也會發生移動。通過圖2(b)可以觀察得到，輸出特性P-U 曲線出現了3 個峰值，當輸出電壓為20.88 V 時，才是全局的最大功率點，其余兩個峰值點稱為局部最大功率點。如果采用傳統的MPPT 算法，比如擾動觀察法，很難找到最大功率點，或者陷入局部最優點，造成能量損失，從而降低光伏發電的效率。

圖2 局部遮陰情況下光伏陣列輸出特性

2 混合算法

為了增加跟蹤速度、減少算法計算量，本文采用“兩步走”MPPT 控制策略。第一步，使用PSO-GA 結合算法，設定少量的迭代次數，找到全局最大功率點的范圍區間。第二步，使用模糊控制在該區間內找到最大功率點，并且穩定，防止因為在最大功率點處振蕩帶來的能量損失。

2.1 PSO-GA 算法

采用粒子群算法和遺傳算法相結合進行一個全局尋優搜尋。由于遺傳算法的隨機性，它不能提供問題的精確解，它需要復雜和耗時的計算才能收斂。相比之下，粒子群算法可以通過比較粒子的位置與周圍位置以及粒子的全局位置來達到精確解。但是，如果使用不當，在高維空間中可能陷入局部最優。遺傳算法通過交叉和變異得到各種解，彌補了粒子群優化算法的不足。同時，粒子群算法通過加快計算速度和提高計算精度來彌補遺傳算法的不足[8]。為此，提出了一種粒子群和遺傳結合的混合算法，如圖3 所示。該算法具有粒子群優化算法的速度和精度以及遺傳算法的多樣性。

圖3 PSO-GA混合算法流程

第一步，在搜索空間上隨機生成初始解。粒子x0的初始位置也由[xmin,xmax]范圍內的均勻分布生成，其中xmin和xmax分別為變量的上下界。

第二步，將粒子群算法應用于初始種群。每個粒子的位置和速度是根據單個粒子的經驗和其他粒子的經驗來確定的。該算法對結果進行排序，并保存用于快速收斂的最佳和最差解。對初始種群進行評估，并根據Pbest和gbest的值對種群進行排序。Pbest是每次迭代中的最佳解，gbest是所有迭代中的最佳解。

第三步，將遺傳算法應用于剩余的低秩粒子。在每次迭代中，遺傳算法通過交叉和變異操作生成一個新的種群。最后，將遺傳算法和粒子群優化算法生成的種群組合起來，進行下一次迭代。這種組合被用作下一次迭代的初始解。算法將在特定的迭代次數后停止。

2.2 模糊控制

對于光伏系統，由1.1 節可知，太陽的輻照度和溫度的變化都會影響光伏陣列的輸出功率。而且這兩個參數未知性很大，難以預測。與傳統的MPPT 控制算法不同，模糊控制法對大氣突變具有魯棒性，不需要建立精確的數學模型。本文利用模糊控制算法進行MPPT，所提出的控制算法是離線控制算法，不需要依賴大量的數據學習[9]。本文以功率變化量與電壓變化量之比為變化比率E，E(t)與上一個時刻E(t-1)的差值定義為ΔE，以E和ΔE這兩部分作為模糊控制的輸入，以占空比變化量ΔD作為輸出。

在模糊控制算法中，由式(1)和式(2)計算模糊控制算法輸入E和ΔE。

式中：PPV(t)和VPV(t)分別為光伏組件的輸出功率和電壓。

2.2.1 隸屬度函數的確定

輸入變量和輸出變量的隸屬度函數均采用三角形來定義。通過測量輸入變量E和ΔE，并將數字表示形式的輸入量量化為通常用語言值表示的某一限定碼的序數。每一個限定碼表示集合論域內的一個模糊子集。

第一步，辨識模糊控制的所有輸入輸出變量，其中橫坐標為輸入變量與輸出變量相比的集合論域。縱坐標為隸屬度函數，其范圍為0～1。輸入變量E和ΔE定義7 個模糊子集：負 大(NB)、負 中(NM)、負 小(NS)、零(ZO)、正 小(PS)、正 中(PM)、正大(PB)，如圖4(a)、(b)所示[10]。

圖4 輸入變量的隸屬度函數定義

根據控制經驗，將E和ΔE量化為離散論域，取值如下：

為了使最大功率點處有更小的抖動，本文設置ΔE的隸屬度函數在越靠近最大功率點處，三角形隸屬度函數越密集，反之越稀疏。

對于輸出變量占空比ΔD也定義了7 個模糊子集：負大(NB)、負中(NM)、負小(NS)、零(ZO)、正小(PS)、正中(PM)、正大(PB)，隸屬度函數如圖4(c)所示。

2.2.2 模糊規則設計

對于模糊規則的選取，按照“if and then”的原則來進行設計。根據控制經驗，模糊規則設計如表1。

表1 模糊規則

對應Matlab 的模糊控制設計如圖5 所示，“And”方法設置為min，“Or”方法設置為max，解模糊設定為重心法。根據表1 的模糊規則對應了49 條模糊規則語句，設定如圖5 所示。

圖5 Matlab模糊規則設計

3 仿真及實驗結果

根據“兩步走”MPPT 控制策略，搭建Simulink 仿真模型，如圖6 所示。根據不斷的實驗測試，本文設定粒子群和遺傳算法的迭代次數為30 次。可以減少計算量，并且能找到全局最大功率點附近，通過一個判斷模塊進行切換，轉化為模糊控制搜尋至最大功率點，并穩定。

圖6 “兩步走”MPPT控制仿真模型

為了驗證該方法提出的有效性，將基于擾動觀察法、電導增量法、擾動觀察結合模糊控制法，變步長電導增量結合粒子群算法，以及提出的混合控制算法進行了仿真對比驗證。

在這種情況下，t=1 s時，輻照度從1 000 W/m2到800 W/m2，在t=1.5 s 時，輻照度變到600 W/m2，最后在t=2 s 時恢復到1 000 W/m2。如圖7(a)所示，所提出的混合算法在t=0.2 s 時達到其最優點，擾動觀察法和電導增量法分別在0.48 s 和0.54 s 時達到最優，這清楚地表明提出的混合算法在局部遮陰(光照幅度變化時)其性能優于電導增量法和擾動觀察法。圖7(b)顯示了光伏系統輸出功率的變化。所提出的混合算法可以在1 000 W/m2、25 ℃條件下使光伏陣列輸出的功率達到98.70 kW，變步長增量結合粒子群算法可以達到96.03 kW，擾動結合模糊控制法輸出功率為95.09 kW，電導增量法和擾動觀察法輸出功率分別為94.52 和90.13 kW。

圖7 模糊控制算法隸屬度函數的優化結果

根據分析，在不同的輻照度下出現多峰值情況，所提出的混合算法比另外幾種更有優勢，提高了輸出功率，縮短了跟蹤時間。如表2所示，當光照幅度在1 000 W/m2、25 ℃情況下，該算法比擾動結合模糊控制法提高了3.6%[(98.70-95.09)/98.70=3.6%]，比變步長增量結合粒子群算法提高了2.7% [(98.70-96.03)/98.70=2.7%]。驗證了本文所提出算法的優越性。

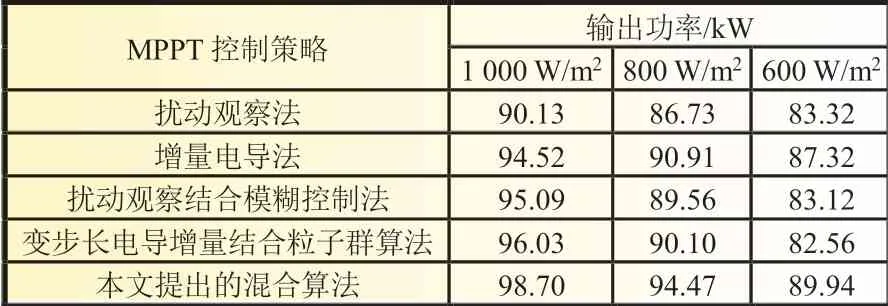
表2 變輻照度恒溫度MPPT 控制算法的比較

4 結論

針對局部遮陰情況下出現的多峰值問題，本文提出了一種混合算法來跟蹤全局最大功率點，從而提高光伏發電效率。采用“兩步走”策略，首先利用粒子群結合遺傳算法，使用少量的迭代次數搜尋至全局最大功率點附近；再切換至模糊控制算法，跟蹤到最大功率點。利用Matlab/Simulink 仿真驗證，該算法比擾動結合模糊控制法輸出功率提高了3.6%，比變步長增量結合粒子群算法提高了2.7%，驗證了該混合算法的可行性。通過跟蹤時間對比，所提出的混合算法也有較優的跟蹤性能和響應速度。