基于改進脊線法的超冗余機器臂逆運動學求解*

潘 健，郭忠峰，王赫瑩(沈陽工業大學遼寧省智能制造與工業機器人重點實驗室，遼寧 沈陽 110870)

0 引言

機器人已廣泛地應用于各個領域，傳統串并聯機器人由于尺寸和靈活性限制難以適用于復雜狹窄的作業環境，超冗余機械臂因其具有良好的環境適應性和避障能力[1]，逐漸成為機器人領域研究的熱點。

國外對超冗余機械臂的研究起步較早，1991年，Chikjian和Burdick最先提出“超冗余”一詞[2]，后續許多團隊設計了不同的機械結構。Walker及其團隊[3-5]開發了一種線驅動機械臂，并建立了運動學模型，英國OC Robotics公司[6-7]先后研發了多款超冗余機器人，用于飛機零部件組裝、狹小空間焊接切割等。國內對超冗余機械臂的研究比國外晚，主要的研究單位有哈爾濱工業大學、沈陽自動化研究所、北京航天航空大學[8-10]等。超冗余機械臂因其自由度數多，所以逆運動學求解困難，傳統的廣義逆法求解超冗余機械臂運動學存在計算量巨大甚至無法求解的問題[11]，針對這一問題，Chikjian和Burdick于1994年提出了基于脊線的逆運動學求解算法并應用于超冗余機械臂的逆運動學求解[12]，但是該方法將機械臂關節盡可能的擬合在脊線上，導致機械臂喪失了許多自由度。

本文針對傳統機器人尺寸大、靈活性不足的缺點，設計了一款基于新型球形關節串聯而成的超冗余機器臂，以其為基礎，提出一種基于改進脊線法的超冗余機械臂逆運動學求解算法，用于新型超冗余機械臂操作空間和關節空間之間的逆運動學求解，利用Matlab對空間脊線及機械臂逆運動學進行數值仿真。

1 新型超冗余機器臂結構設計

1.1 整體結構設計

新型超冗余機器臂整體機械結構如圖1所示，整個機械系統由機械臂模塊和驅動模塊組成。

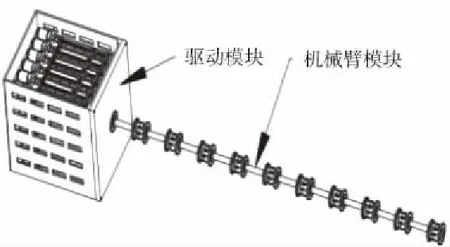
圖1 超冗余機器人機械系統原理圖

機械臂模塊由10個模塊化單關節串聯而成，每個模塊化單關節具有兩個自由度，機械臂的末端可以安裝機械抓手和攝像頭。驅動模塊采用箱體式結構，內置30個電機采用分層布置方式，每一層6個電機，分為5層，機械臂通過法蘭與驅動模塊箱體連接。

1.2 驅動部分結構設計

驅動模塊的單層驅動結構示意圖如圖2所示，底座上等間距安裝6個電機，電機輸出端通過聯軸器與絲杠連接，機械臂關節的驅動繩索通過雙U形槽輪導線裝置與絲杠螺母上的壓線裝置連接，通過絲杠螺母的直線運動可以實現驅動繩索的拉緊和放松。

圖2 單層驅動模塊結構示意圖

1.3 球形關節結構設計

新型超冗余機械臂由10個新型球型關節串聯而成，新型球型關節的結構如圖3所示。

圖3 新型球形結構示意圖

一個新型球型關節包括中間球體及兩端與之配合的導繩盤，中間球體上均勻設置4個半球形軌道，導繩盤上與中間球體配合的內球面上兩側分別設置兩個半球形孔用于安裝滾珠，實現導繩盤在中間球體軌道上的滾動，可以減小關節運動時的摩擦損耗，提高關節使用壽命，導繩盤兩側的側耳上設置螺紋孔，用于擋塊和導繩盤側耳的連接。關節與關節之間用法蘭連桿連接，單關節長度為150 mm，新型球型關節的單自由度旋轉角度范圍為[-30°，30°]。新型超冗余機械臂直徑為50 mm，中間球體、導繩盤、連桿中心軸線方向均采用空心結構，減輕了整個機械臂的重量，同時電纜可由機械臂中心穿過，實現末端電子設備的供電和信號傳輸。機械臂采用電機外置三線驅動方式，三根繩索呈120°布置，每個導繩盤上均勻布置導繩孔，驅動繩索直徑為1.2 mm。

2 基于改進脊線法的超冗余機械臂逆運動學求解

2.1 空間脊線模型

圖4 空間脊線示意圖

空間脊線是一條可以描述超冗余機械臂空間形態的曲線[13]，其示意圖如圖4所示。

空間脊線的數學表達式[14-16]可描述為：

(1)

式中：s為歸一化脊線長度的參數；X(0)為脊線的起點位置；X(1)為脊線的終點位置；L為脊線的實際長度；u(σ)為脊線在點σ處的脊線切線向量。

空間脊線的切線向量u(σ)可以表示成：

(2)

其中，ψ(σ)為空間線段Oσ與其在XOY平面上投影之間的夾角，φ(σ)為空間線段Oσ在XOY平面上投影與Y軸之間的夾角。

2.2 空間脊線運動學

脊線的運動學是研究脊線參數與脊線末端點之間的關系，而到達空間一點不止一條脊線，因此需要對脊線形狀進行限制，令{si(s)}為對應的脊線形狀約束方程：

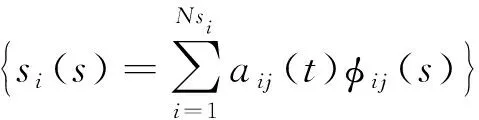
(3)

式中：Nsi為模態子方程的個數；aij(t)為模態協同參數；φij(s)為模態子方程。

由于空間脊線方程表達式比較復雜，協同參數一般無法由顯示方程求解，因此采用數值方法求解空間脊線協同參數，下面簡述脊線協同參數的求解過程。

脊線方程對時間t求導得：

(4)

式中：J(a)為脊線的模態雅克比矩陣，是脊線協同參數的函數。

(4)式用來求解t時刻脊線協同參數集合a。

上述脊線協同參數求解可能會使脊線末端位姿產生較大的誤差，因此需要對協同參數進行修正，下面采用迭代法進行參數修正。

ak+1=ak+α·J-1(ak)·[XD-X(ak)]

(5)

式中：J-1(ak)為模態雅克比矩陣的逆矩；ak為第k次迭代a的計算值；XD為脊線的末端點位置；X(ak)為當ak為脊線協同參數時計算出的脊線末端位置；α為常數，控制迭代收斂速度。

脊線運動學描述：正運動學是已知脊線的模態協同參數求解脊線的末端位置；脊線的逆運動學是已知脊線的末端位置求解脊線的模態協同參數。

2.3 超冗余機械臂關節位置擬合

本文提出基于障礙物位置的機械臂關節擬合方法，關節擬合示意圖如圖5所示，擬合過程主要包含三個步驟：末端關節擬合；剩余關節預擬合；局部關節位置調整。

圖5 機械臂關節擬合示意圖

2.3.1 末端關節擬合

為使脊線末端指向與機械臂末端執行器指向相匹配，假定機械臂末端執行器指向方向的單位向量為kn，末端位置坐標為Xe=[xeyeze]T，機械臂總長度為l，關節數為n，則機械臂末端關節的位置坐標為：

Xn=[xnynzn]T=Xe-kn·l/n

(6)

2.3.2 剩余關節位置預擬合

為使剩余關節盡可能地落在或者接近脊線，對剩余關節位置進行預擬合，由于靠近機械臂始端的關節位置由后一關節的位置和關節長度決定，所以在剩余關節擬合時由機械臂末端關節向機械臂始端關節開始擬合，假設機械臂任意關節i的位置坐標為Xi=[xiyizi]T，其中i∈[3，n-1]，以點ji+1為球心，以l/n為半徑作球體，與脊線相交于一點ji，以點ji為關節i的擬合點，以點ji到點ji+1之間的脊線的內接弦向量li作為關節i的擬合量，則關節i的位置向量可以表示為：

Xi=Xi+1-li

(7)

由(7)式可以推導i≥3關節的位置向量，為了保證i≥3關節都擬合在脊線上，取各段脊線的內接弦作為擬合量，當k=2時，剩余脊線的長度會小于2L/n，導致關節2無法擬合到脊線上，取點j2、j1分別為關節1、2的擬合點，其中關節1為原點。

圖6 關節2擬合 示意圖

如圖6所示，分別以點j1、j3為球心，以l/n為半徑作球體，兩個球體的交線為空間圓，在該圓上求解一點j2，使得j2到脊線的距離最短。以j2為關節2的擬合點，點j2到點j3之間的線段作l2為關節2的擬合量，點j2到點j1之間的線段l1作為關節1的擬合量，關節2的位置向量可以表示為：

X2=X3-l2

(8)

2.3.3 局部關節位置調整

在預擬合過程中，機械臂所有的關節接近或落在脊線上，對于無障礙路徑，這種擬合求解方法可以減少計算量，但是對于有障礙路徑，這種擬合求解方法由于犧牲了大量自由度而導致機械臂喪失靈活性，故本文提出基于障礙物位置的關節擬合算法，即引入障礙物參數(包括障礙物位置參數和尺寸參數)，對局部關節位置進行調整。

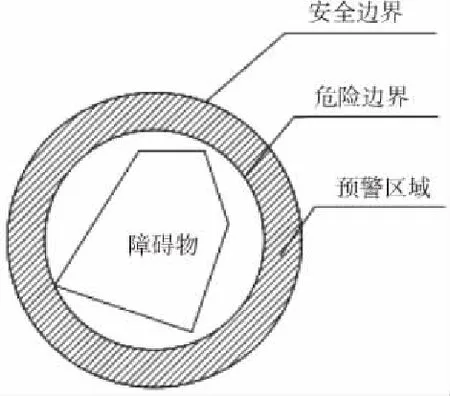
圖7 障礙物模型示意圖

如圖7所示，首先對障礙物進行建模，為了便于描述機械臂關節與障礙物之間的位置關系，將障礙物的外接球面視為機械臂所能到達的極限位置，稱之為危險邊界，其半徑為Rw，同時，為了保證機械臂運動過程中的絕對安全，在危險邊界周圍設置預警區域，預警區域的外圍邊界是機械臂的安全運動邊界，其半徑為Ra。在一般工況下，要求機械臂絕對安全運行，所以機械臂關節要始終處于安全邊界之外。

假設機械臂第i個關節ji處于安全邊界范圍之內，為了使機械臂安全運行，需要對機械臂關節ji的位置進行調整，調整后的關節需要滿足以下邊界條件：

(9)

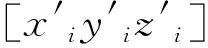
根據上述條件限制，求解得到一系列滿足條件的關節空間位置坐標后，為了使調整后的關節更好地與脊線吻合，在上述邊界條件的解集中確定調整后關節的位置，使其滿足到預擬合確定的關節ji位置的歐氏距離最小，將該位置作為調節后的關節位置，即滿足下列公式：

(10)

同樣地，對于復雜工況環境，若同時出現多個關節在安全邊界以內，則可以引入多組障礙物參數，應用同樣的方法對多個關節位置進行調整。

2.4 超冗余機械臂關節變量求解

求得各個關節擬合后的位置坐標后，下面求解關節k的旋轉角度θk、θ2k，結合常用的D-H坐標系法進行關節變量求解，以本文設計的新型超冗余機械臂為例，建立機械臂的D-H坐標系如圖8所示，得到各個關節的D-H參數如表1所示。

圖8 新型超冗余機械臂D-H坐標系

表1 新型超冗余機械臂關節D-H參數

(11)

式中，c*是cosθ*的簡寫，s*是sinθ*的簡寫。

對于1關節，可以通過下式求解旋轉角度θ1、θ2。

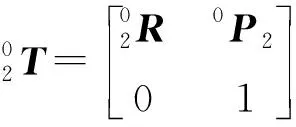
(12)

X1=0P2

(13)

(14)

Xk=0P2k

(15)

在上述關節旋轉角度求解過程中，因為末端關節求解時用到前面關節的旋轉角度變量，所以求解時需要從首端關節到末端關節依次求解。

3 空間脊線與機械臂逆運動學仿真

3.1 空間脊線仿真

根據超冗余機械臂的結構特點，本文選取模式函數為：

(16)

脊線約束方程為：

(17)

任意給定脊線的末端位置，在上述約束方程的約束下可以求解出空間唯一一條脊線與之對應，假設給定脊線的末端位置為空間圓，其方程為：

根據給定的脊線末端點位置，本文通過數值方法(newton法)求解脊線的協同參數，得到空間脊線方程，在matlab中繪制空間脊線的三維圖形(圖9)及XY平面投影(圖10)，脊線較光滑，沒有曲率較小的脊線段，因此超冗余機械臂可以與脊線很好的擬合。

圖9 空間脊線三維圖 圖10 空間脊線YZ平面投影圖

3.2 機械臂逆運動學仿真

為了驗證本文提出的基于改進脊線法的超冗余機械臂逆運動學算法的有效性，本文用matlab進行仿真計算。設置機械臂參數：機械臂的末端位置為X=[600，450，900]T，歸一化后對應脊線的末端為：

Xd=[0.4，0.3，0.6]T

設置障礙物參數：障礙物模型1的位置為[290，550，255]T，半徑為30 mm，障礙物模型2的位置為[485，550，480]T，半徑為30 mm。歸一化后對應的障礙物參數為：

Xa1=[0.193，0.367，0.170]TRa1=0.02

Xa2=[0.323，0.367，0.320]TRa2=0.02

根據本文所提出的改進脊線逆運動學求解算法和空間超冗余機械臂擬合算法進行超冗余機械臂逆運動學求解并通過matlab仿真，結果如圖11所示，圖中實線曲線表示空間脊線，虛線折線表示機械臂中心線的擬合，每個折線段表示機械臂連桿的位置，圓圈表示超冗余機械臂關節。

圖11 基于改進脊線法逆運動學仿真結果

根據本文所提出的機械臂關節自由度求解算法，通過matlab求解各個關節的自由度變量，運用matlab機器人工具箱函數robot.plot()繪制超冗余機械臂空間構型，如圖12所示。

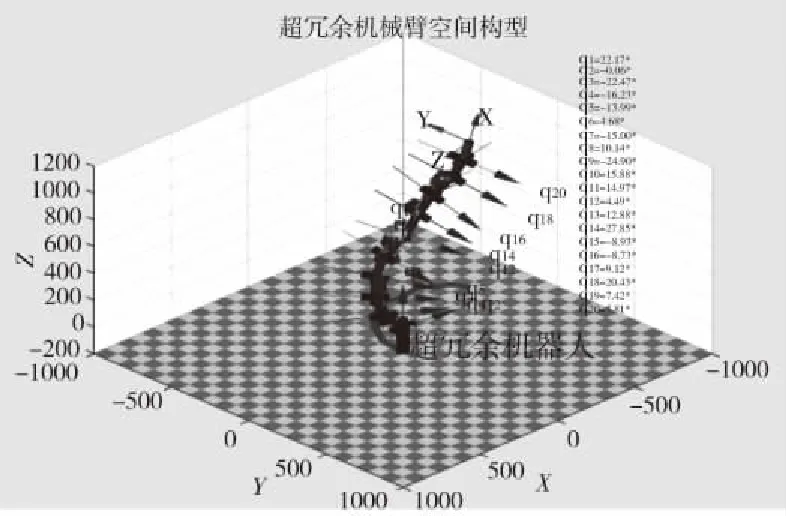
圖12 新型超冗余機械臂空間構型圖

4 結論

本文設計了一款基于新型球形關節串聯而成的超冗余機械臂，提出了一種基于改進脊線法的超冗余機械臂逆運動學求解算法，并且結合D-H坐標系法，完成了各個關節變量的求解及仿真，為進一步對超冗余機械臂運動學及動力學分析奠定了基礎。