正常狀態下盾尾密封油脂腔壓力分布特性研究*

王林濤，鈄 婧，孫開欣，王 寧，郭正剛(大連理工大學機械工程學院，遼寧 大連 116023)

盾構法施工以其安全、高效的特點，已成為隧道掘進工程中一種重要的施工方法[1]。這種工法施工通過采用盾殼支撐前方和上部土體，并采用密封措施防止盾殼外部水土侵入盾體內，從而可有效地保證盾構施工人員的安全。后盾與管片之間的密封稱為盾尾密封。盾尾密封系統一旦破壞，則盾體外的水土、背填漿液很容易穿透盾尾密封進入盾體內，出現盾尾漏漿、漏水現象。為了研制盾尾泄漏監測與預警技術，在盾尾結構限制下無法直接監測到泄漏現象，只能通過布設壓力傳感器監測壓力變化來發現泄漏部位。

目前盾構盾尾密封通常采用尾刷+充填油脂的形式，尾刷由3道鋼絲刷組成，尾刷與盾體、管片一起形成2個空腔，空腔內注入油脂充填，從而起到阻隔盾體外注漿材料和地層中的水、土的作用[3]。由于盾尾密封刷是彈簧板+鋼絲束+彈簧板的結構，受力時的形態難以確定，且在盾尾間隙之間，每兩個盾尾刷之間采用的是焊接的方式形成一環密封刷。因此，每道盾尾密封刷受到前后腔體內流體壓力作用時變形規律都不是相同的，盾尾刷的密封性能難以檢測和確定。而密封油脂是一種帶有塑性的非牛頓流體，目前沒有準確的參數可以描述它的流體性能。在盾尾密封腔內的油脂建立起壓力，與刷絲間充填油脂的盾尾密封刷共同組成盾尾密封系統。盾尾密封油脂腔的壓力分布結果是研究盾尾密封刷變形規律的前提，且對盾尾密封系統的傳感器布設有指導性意義。所以，盾尾密封油脂腔的壓力分布特性研究是非常有必要的，它是研究整個盾尾密封系統密封性能的需求前提，為盾尾密封系統失效安全預警技術研究提供理論基礎。

針對盾尾密封系統，國內外學者主要在盾尾密封油脂和盾尾密封刷方面有一定的理論和實驗研究。國內外典型的盾尾密封油脂材料有法國CONDAT盾尾密封油脂、日本松井TAIL SEALER盾尾密封油脂、“上隧牌”盾尾密封油脂等，而王德乾[4-5]、白傳航[6]、叢恩偉[7]、盧少華等[8]都根據實際工程項目的原理需求，在不同程度上研發出新型的盾尾密封油脂或優化了原有的密封油脂配方；歐洲噴射混凝土標準(EFNARC)、美國Jacopo Franchini等、日本松井公司、中鐵五院、石家莊鐵道大學嚴振林等[9]各自設計了原理相似的油脂耐水壓密封性檢測裝置，并提出相應的盾尾密封油脂耐水壓密封性檢測方法；饒竹紅等[10]在現有的油脂耐水壓密封性檢測方法和現有裝置的基礎上，利用了計算流體動力學的分析軟件FLUENT計算分析了盾尾密封油脂在水密性裝置中的流動性規律；李奕[11]、霍志光[12]對傳統盾尾密封刷進行了結構上的優化改進，李大偉等[13]研制了能夠測試盾尾密封刷的耐磨性能和彈性的綜合實驗平臺；高振峰等[14]依據油脂耐水壓特性建立盾尾密封二維數值模型，將盾尾密封刷對密封油脂的阻礙作用等效成多孔介質區域的作用，得到滲漏過程中的油脂流動分布與壓力變化規律；鐘波等[15]通過建立盾尾刷的三維有限元模型，對盾尾刷在不同間隙和不同壓力下的工作性能進行了有限元分析。上述研究主要集中于盾尾密封油脂和盾尾密封刷的自身特性研究，沒有結合兩者的特性分析盾尾密封系統的密封性能，也沒有根據實際結構和工況分析密封系統的壓力分布特性和影響因素。

本文運用計算流體力學方法，開展盾尾密封系統在正常工作狀態下的油脂壓力分布規律和影響因素等理論研究。基于實際工程所用盾構機的結構尺寸建立盾尾密封系統全尺度三維仿真模型，通過改變結構參數、工況參數來研究盾尾密封系統正常狀態下壓力分布特性的影響因素與影響規律，為大型掘進機施工安全關鍵系統監測與預警技術研究提供理論支撐。

1 盾尾密封系統流體模型

1.1 盾尾密封建模理論

1.1.1 流體動力學控制方程

在盾尾密封系統的油脂密封原理正常工作的工況下，流體動力學方程應滿足流動基本方程，包括質量守恒方程、動量守恒方程和能量守恒方程[16]：

(1)

(2)

(3)

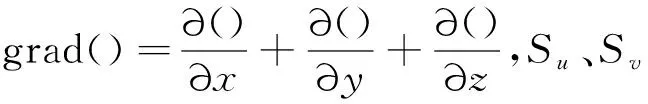
1.1.2 多孔介質模型

FLUENT軟件在計算多孔介質時是給多孔介質的方程中添加一個動量源相，這個動量源相中包含了兩部分，粘性阻力和慣性阻力。

(4)

式中，等號右側第一項為粘性阻力，第二項為慣性阻力。其中，μ為流體粘度，v為速度，Dij和Cij為矩陣。將上式中的矩陣用系數進行代替即為：

(5)

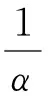
ΔP=a·v2+b·v

(6)

將式(5)與式(6)進行對比可得：

(7)

其中，ρ為流體密度，Δn為多孔介質厚度。

若只考慮粘性阻力效應，多孔介質模型變為線性化的Darcian模型：

(8)

1.2 盾尾密封數值求解模型

1.2.1 三維求解模型

本文以某實際工程所用某型土壓平衡盾構機的盾尾密封系統為研究對象，基于圖1所示的盾尾密封原理，對其進行參數化建模，建立了盾尾密封系統流場三維仿真物理模型，如圖2所示。為了簡化盾尾刷露出刷絲部分的流體計算，將這部分簡化為多孔介質區域，使其可在流體計算時發揮作用。

圖1 盾尾密封原理示意圖

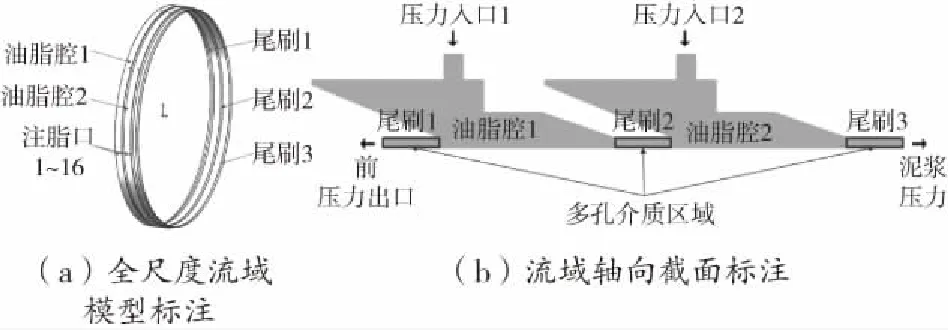
圖2 盾尾密封油脂腔三維仿真物理模型

1.2.2 網格劃分

網格劃分采用mesh模塊的自動網格劃分方法，多孔介質區域采用六邊形網格，油脂入口處網格尺寸比周圍網格的尺寸小，達到網格細化效果，流體域網格如圖3所示。對模型進行了網格無關性驗證，考慮網格質量、分析精度和計算時間等因素，最終選定全局單元尺寸為20 mm，局部單元尺寸為10 mm，網格數量為192萬，平均單元質量為0.8207。

圖3 盾尾密封流體域網格模型

1.2.3 邊界條件

盾尾密封油脂腔的油脂控制有兩種控制方式，壓力控制和流量控制。油脂泵通過管道將油脂輸送到各個腔室，一般采用壓力控制方式確保密封所需壓力。初始模型設置參數與邊界條件如表1所示。

表1 初始模型設置參數與邊界條件

2 模型驗證

2.1 密封油脂流體模型驗證

非牛頓流體是指剪切應力和剪切變形速率之間不滿足線性關系的流體[19]，盾尾密封系統所用的密封油脂就是一種帶有塑性的非牛頓流體。在常用的非牛頓流體模型中，Herschel-Bulkley模型是具有Power-Law流體性質的Bingham模型，當剪切應力超過屈服強度τ0時，流體按照Power-Law模型的本構關系流動：

(9)

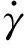
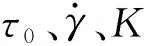
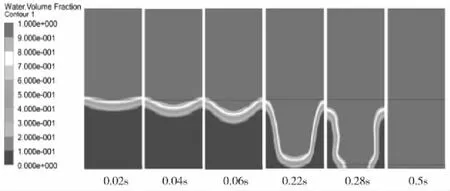
圖4 油脂流動規律(深色部分為油脂)

2.2 多孔介質模型驗證

由經驗數值[20]可知，密封油脂的平均消耗量約為每平方米管片表面消耗0.8 ～1.3 kg，若主機最大掘進速度為80 mm/min，管片外徑為6900 mm，那么單位時間內油脂最大消耗量Gmax和最小消耗量Gmin為：

Gmax=80×3.14×6900×1.3/106=2.25 kg/min=0.0375 kg/s

Gmin=80×3.14×6900×0.8/106=1.39 kg/min=0.0232 kg/s

仿真模擬時設定正常注脂壓力入口為3 bar，注漿壓力為2 bar，得到出口流量結果如表2所示。

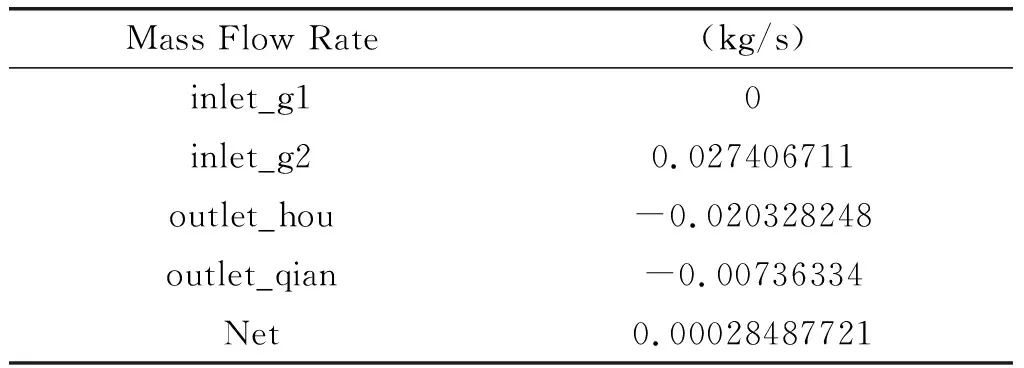
表2 質量流量計算結果

可得到入口流量約為0.02741 kg/s，出口流量約為0.02769 kg/s，誤差為0.00028 kg/s，約1%，在允許范圍之內。仿真得到的平均流量值0.0275 kg/s，處于油脂消耗量范圍0.0232～0.0375 kg/s之內，證明了利用多孔介質模型代替盾尾密封刷的阻礙作用的合理性和可行性。

2.3 模型簡化驗證

根據三維仿真模型的對稱性質，截取全尺度模型的四分之一作為分析所用局部模型，如圖5所示。

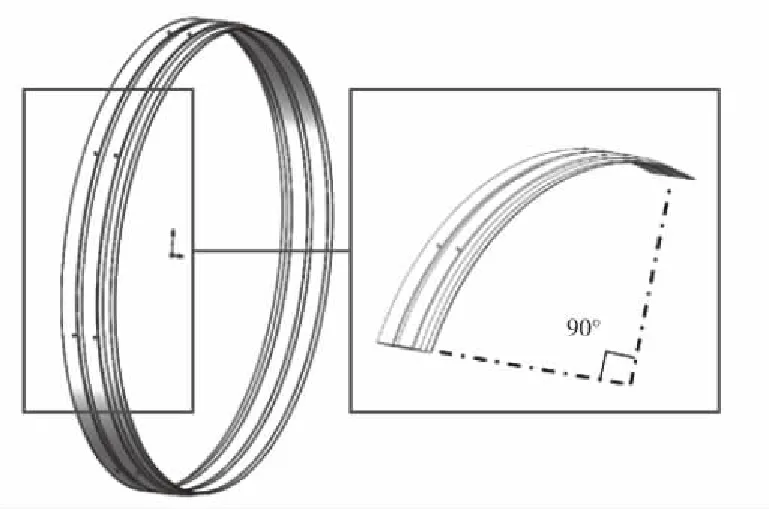
圖5 四分之一模型

相同參數設置條件下，全尺度模型與局部模型的計算結果對比如表3所示，結果誤差在允許范圍(誤差<2%)內，驗證了局部模型的可行性。

表3 結果驗證

3 油脂腔壓力特性分析

3.1 正常狀態壓力分布規律

盾尾密封油脂腔采用壓力控制方式，按照油脂注入壓力控制原則將邊界條件設定為：油脂腔1壓力入口為2 bar，油脂腔2壓力入口為3 bar，前壓力出口為1 bar，注漿壓力(后壓力出口)為2 bar。得到的油脂腔2入口處兩方向截面壓力分布云圖如圖6所示。根據圖示，觀察周向截面壓力值在曲線y2+z2=35002mm和線段O1O2上的變化情況，O2點為兩線交點。

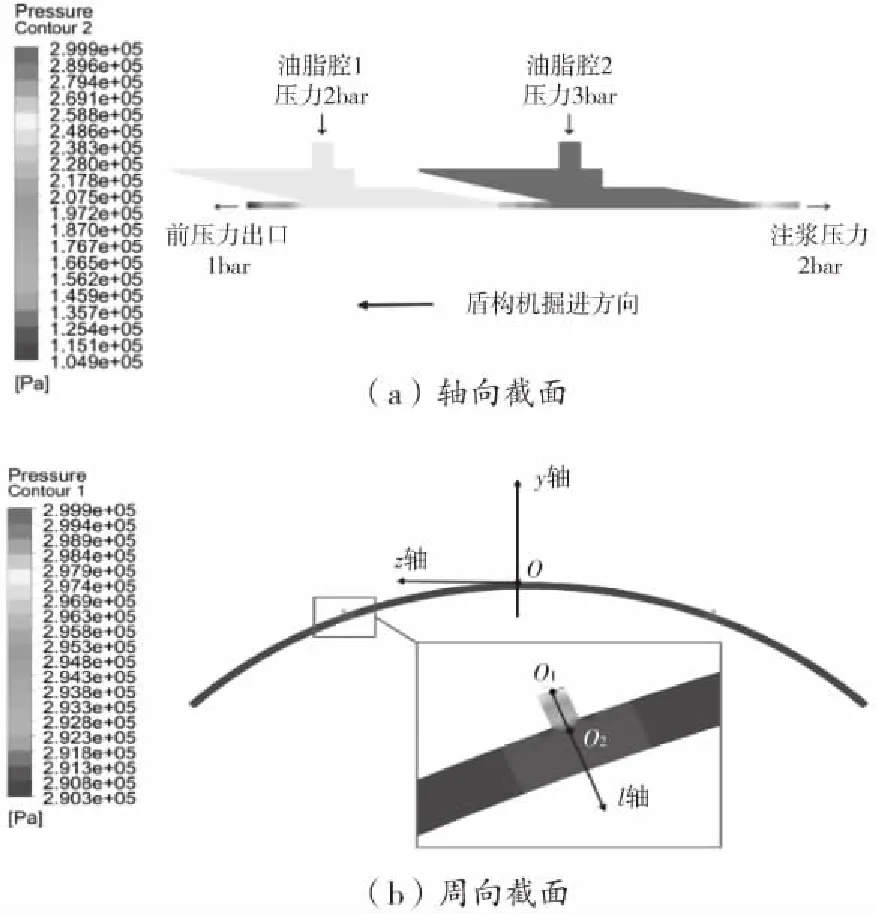
圖6 油脂腔壓力分布云圖

從軸向截面壓力云圖可以看出，油脂從入口處往油脂腔內充填，進入油脂腔后油脂沿著盾構機行進方向前后擴散，多孔介質區域對壓力有阻礙作用，油脂腔內的壓力從入口處的最高點沿軸向的前后向低壓出口位置遞減。而周向截面壓力分布規律為：油脂從入口處往圓心方向遞減，入口處為設定的入口壓力，越往腔內充填壓力越小，變化情況如圖7(a)所示；在入口處兩側，油脂腔內的壓力從入口處的最高點沿周向兩側低壓位置遞減，油脂壓力沿著圓周方向下降的趨勢和幅度大致相同且分布區域呈對稱形式，以至于在兩個入口的中軸線位置，壓力達到周向的最小值，變化情況如圖7(b)所示。

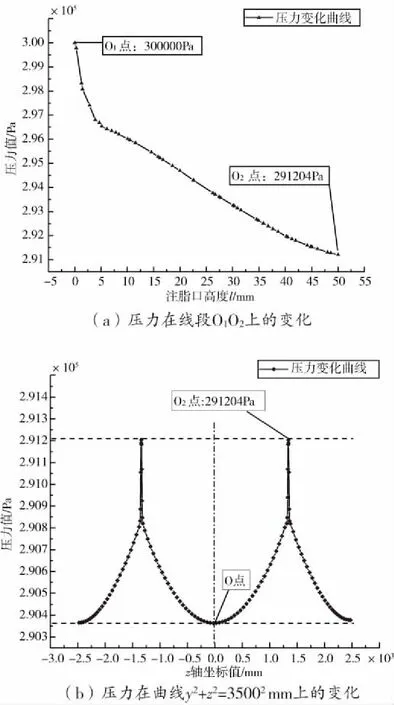
圖7 周向截面油脂入口間壓力變化情況

3.2 油脂壓力分布特性模型設計

3.2.1 變量設計

為了探究油脂壓力分布特性的影響因素，將油脂腔2垂直于入口面的周向壓力差值ΔPc和軸向壓力差值ΔPa設定為輸出參數，選取了盾尾油脂腔的結構參數、模型特性參數和邊界條件參數共12個參數為可變參量，如表4所示。

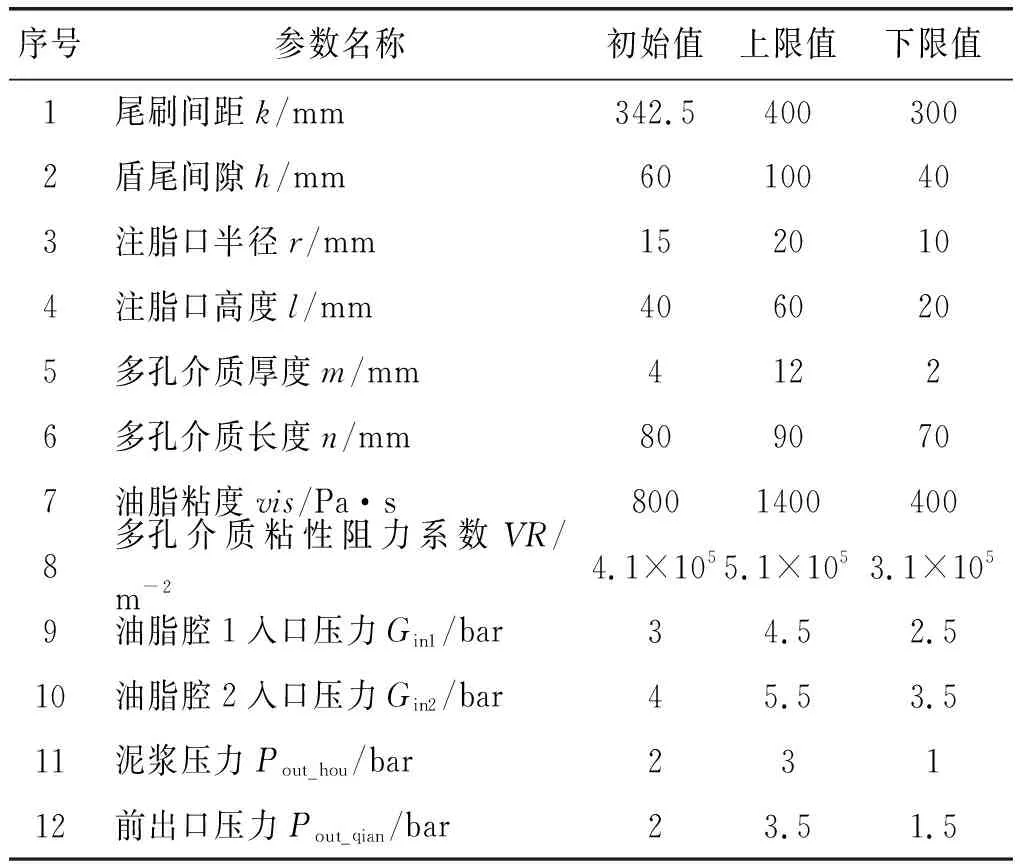
表4 設計變量

3.2.2 響應面模型

DOE試驗設計方法采用拉丁超立方抽樣，生成501個試驗設計樣本點(包含上下限值)，采用Workbench構建GeneticAggregation響應面模型，模型的擬合程度如圖8所示，相關系數R2達到0.998以上，表示模型的擬合程度很好。

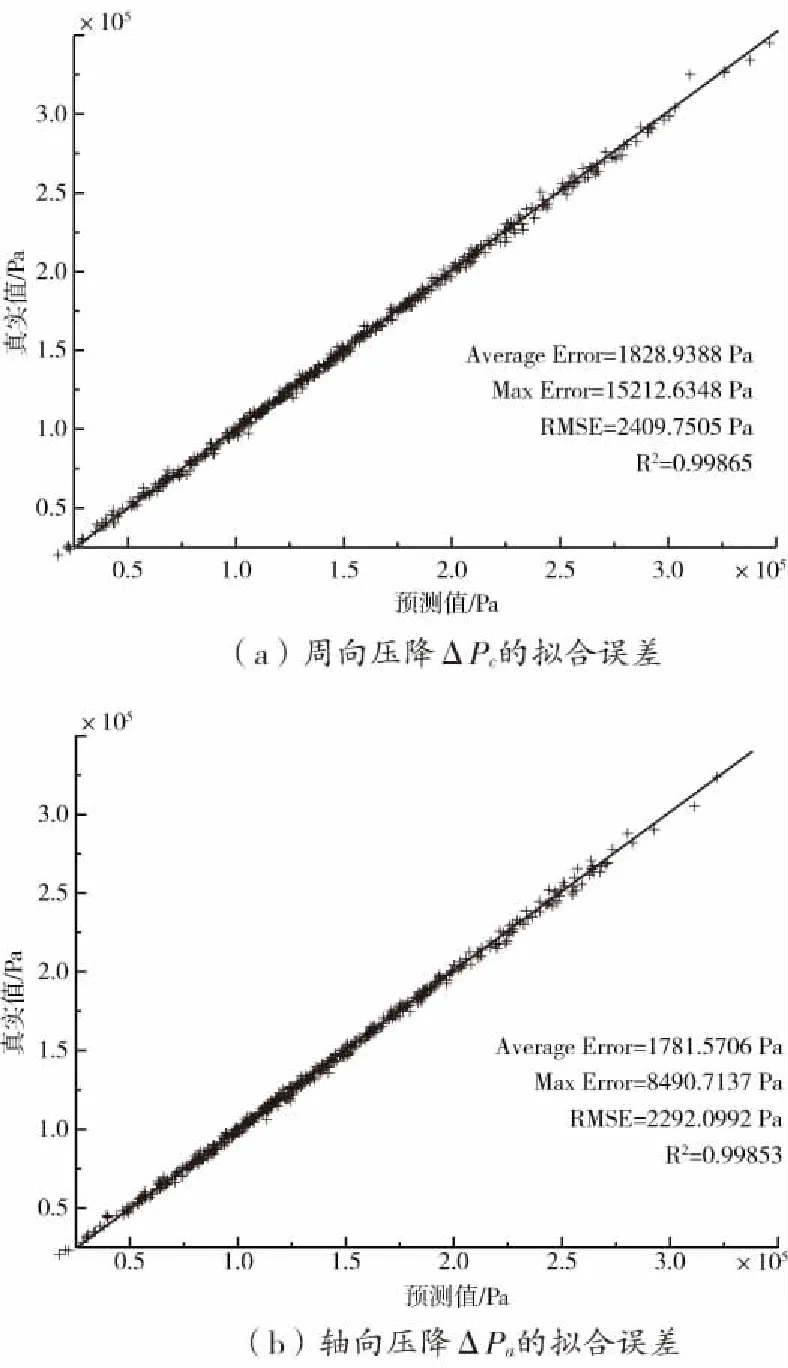
圖8 響應面模型擬合程度

3.3 壓力分布特性的影響因素

3.3.1 結構參數的影響

盾尾密封系統的結構參數在對盾尾密封系統進行設計選型時是必不可少的考慮因素。根據響應面模型的模擬計算，尾刷間距、盾尾間隙等結構參數對周向壓降ΔPc和軸向壓降ΔPa的影響如圖9圖10所示。

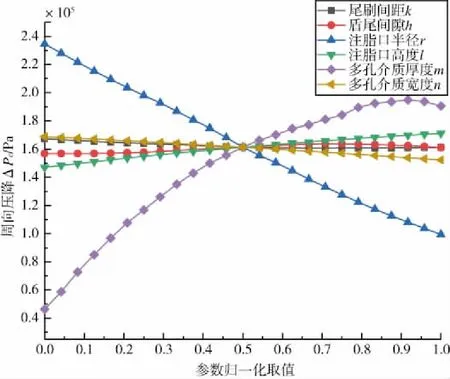
圖9 結構參數對周向壓降ΔPc的影響規律

圖10 結構參數對軸向壓降ΔPa的影響規律

對周向壓降的影響規律圖進行分析，得到以下發現：尾刷間距k、注脂口半徑r、多孔介質厚度n對周向壓降有負向影響，即隨著這些可變參量數值增大，環向壓降減小；但k和n對周向壓降的影響程度較小，r對周向壓降的影響程度較大。盾尾間隙h、注脂口高度l、多孔介質厚度m對周向壓降有正向影響，即隨著這些可變參量數值增大，環向壓降增大；但影響程度最大的是m，h和l的影響程度較小。

對軸向壓降的影響規律圖進行分析，得到以下發現：尾刷間距k改變了油脂腔軸向尺寸，對軸向壓降沒有明顯影響；有負向影響的參量是盾尾間距h、注脂口半徑r、多孔介質厚度n，即隨著這些可變參量數值增大，環向壓降減小，其中影響最大的是r；而注脂口高度l、多孔介質厚度m對軸向壓降有正向影響，即隨著這些可變參量數值增大，軸向壓降增大，其中影響最大的是m。

由于注脂口半徑r影響入口壓力，尾刷多孔介質厚度m影響尾刷的密封性能，才會有相對明顯的影響規律。而注脂口尺寸、尾刷間距屬于不可變結構參數，需要在系統設計時考慮；盾尾間距、尾刷多孔介質厚度屬于可變工況參數，需要在工況變化時考慮這些參數的影響。所以不論影響程度大小，在結構設計、系統優化、監測傳感器布設時都需要考慮這些參數的影響，在可行基礎上選擇最佳的參數配置，保證正常狀態下的密封壓力要求。

3.3.2 模型特性參數的影響

(1)為了探究實際工況下的油脂腔壓力分布規律，就需要考慮到工程所用密封油脂的材料性能，其中最重要的就是粘度vis。由于油脂粘度變化特性相對難測，根據現有文獻資料中的油脂流變試驗測試結果選定油脂粘度研究范圍，探究油脂粘度對壓力分布的影響，結果如圖11所示。

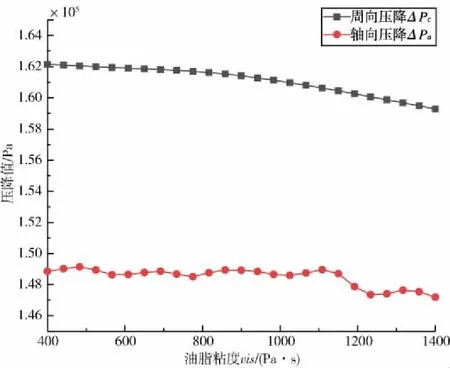
圖11 油脂粘度vis對壓降的影響規律

油脂粘度對周向壓降有明顯的負向影響，隨著油脂粘度增大，周向壓降減小，減小趨勢較為平緩。而從軸向壓降的響應曲線來看，油脂粘度對軸向壓降沒有明顯的影響規律，粘度在1100 Pa·s之前軸向壓降在小范圍內波動，1100 Pa·s之后軸向壓降波動范圍整體下降。但不管是周向還是軸向，壓降變化程度對于基本數值來說都不算大，只要保證盾尾密封系統溫度不驟變，油脂粘度影響的壓降值不超過要求限制即可。

(2)正常狀態下，盾尾刷利用自身彈簧板的反彈力平衡兩側壓力，使油脂從刷絲部分流出而外部泥漿不能侵入油脂腔，簡化之后即是多孔介質模型利用阻力效應控制兩側壓差從而控制出口流量。因為油脂腔內油脂流動緩慢，處于層流狀態，在只考慮粘性阻力效應的情況下，粘性阻力系數對壓降的影響如圖12所示。

圖12 粘性阻力系數VR對壓降的影響規律

不管是周向壓降還是軸向壓降，隨著多孔介質粘性阻力系數的增大，壓降的值總是減小的。顯而易見，粘性阻力效應是替代盾尾刷對油脂的阻礙作用，盾尾刷抵抗變形的能力越強，粘性阻力效應就越明顯。但是在簡化過程中，多孔介質的粘性阻力系數還受到其他因素的影響，比如盾尾間隙、盾尾刷磨損狀態、盾構機推進速度等，在之后的研究工作中可以考慮這些因素的變化對粘性阻力系數以及對壓力分布的影響。

3.3.3 邊界條件對壓力分布的影響

根據油脂注入壓力控制原則，設計了Gin2=Gin1+1bar=Pout_qian+2bar的油脂腔壓力入口條件，使得尾刷多孔介質區域兩側的壓力條件始終滿足原則要求。泥漿注入壓力會改變盾尾刷的受力變形從而對油脂腔2的壓力分布造成影響。邊界條件對油脂腔壓力分布規律的影響如圖13圖14所示。

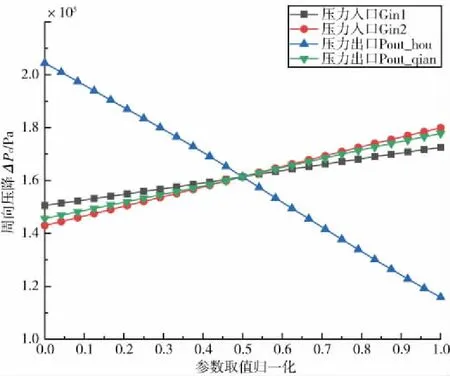
圖13 邊界條件對周向壓降ΔPc的影響規律

圖14 邊界條件對軸向壓降ΔPa的影響規律

從影響曲線很容易看出，油脂腔入口壓力對壓降有正向影響，泥漿壓力對壓降有負向影響。由于在設計變量范圍時考慮了油脂注入壓力控制原則，且在尾刷3兩側總是保持油脂腔入口壓力大于泥漿壓力，邊界條件對環向和軸向壓降的影響有著穩定的規律。但由于只是設定入口壓力大于泥漿壓力，油脂腔壓力分布在環向截面上有壓力最低點，壓力薄弱部分的壓力可能低于泥漿壓力，會造成泥漿侵入油脂腔從而導致密封失效。在研究油脂腔壓力狀態實時監測系統時，就需要在壓力薄弱部分布設壓力傳感器，實時調整注脂、注漿壓力，在最可能失效部位保證每一時刻的油脂耐壓密封性能。

4 結論

本文應用計算流體力學方法，建立了帶有多孔介質區域的盾尾密封系統三維求解模型，分析了盾尾密封油脂腔在正常狀態下的壓力分布規律以及壓力分布特性的影響因素，得出了以下結論：

1)正常狀態下盾尾密封油脂腔的壓力分布規律為：油脂腔內的壓力從入口處的最高點沿圓周方向兩側低壓位置和軸向的前后向低壓出口位置遞減；

2)盾尾密封油脂腔壓力分布特性受到各方面參數的影響且影響程度各有不同，壓力薄弱位置的最小壓力隨參數變化而變化，為盾尾密封系統結構設計、實時壓力監測系統的傳感器布設提供思路；

3)油脂腔在正常狀態下的壓力分布規律為接下來研究受到外部流體侵入時油脂壓力變化及流場特性鋪墊了一定的理論基礎。