基于機器學習的海表溫度對中國降水的預測研究

李良偉，鄒斌，石立堅，劉鵬

（1.國家衛星海洋應用中心，北京 100081；2.國家海洋環境預報中心，北京 100081；3.自然資源部空間海洋遙感與應用重點實驗室，北京 100081；4.南方海洋科學與工程廣東省實驗室，廣東 廣州 511458）

1 引言

海表溫度（Sea Surface Temperature，SST）與降雨有著密不可分的聯系，以往的一些研究集中在降水與局部和區域尺度SST變化關系上。Zahraie等[1]利用K-means聚類算法和遺傳算法（Genetic Algorithm，GA），將阿曼灣、阿拉伯海和印度洋北部選定區域的SST進行聚類，提出了改進的K-means方法和GA模型，該模型可以有效地用于研究區域正常降水的季節預測，這兩種聚類技術的結果已被用于制定伊朗東南部省份的季節性降水預測指南中。Cordery等[2]觀察到一個季節的全球和局部現象與干旱事件的未來4個季節的降水之間有著很強的關系，例如太平洋SST異常可用于預測澳大利亞東部的低降水季節。Higgins等[3]利用熱帶太平洋SST對Nino-3.4地區的氣溫和降水作出了客觀的季節預報，并且跟蹤并比較了這些預測與8 a的觀測結果以及美國國家海洋和大氣管理局（National Oceanic and Atmospheric Administration，NOAA）官方發布的美國氣候預測中心（Climate Prediction Center，CPC）的季節性預報結果的差異。不同時間尺度的SST和海溫大氣耦合系統的震蕩通常會對降雨活動產生重要的影響。對中國降水有影響的包括：季節或年內震蕩，主要是受太陽輻射周期的變化，時間尺度通常為1 a，如季風；年際震蕩，如厄爾尼諾與南方濤動（El Ni?o-Southern Oscillation，ENSO）[4]；年代際震蕩，如太平洋年代際振蕩（Pacific Decadal Oscillation，PDO）[5]，這些震蕩在降水長期預測以及氣候預測中有重要作用。研究指出，ENSO循環對中國降水具有很大影響[6-7]。陶詩言等[7]研究發現ENSO的不同階段對中國夏季降水有不同的影響。王紹武等[8]利用近500 a旱澇資料，指出赤道中太平洋地區年代際變化與中國東部36 a旱澇周期關系密切，從而提出了與海氣相互作用有關的旱澇36 a周期變化機制。于淑秋等[9]應用滑動T檢驗法對北太平洋海溫年代際躍變進行了研究，指出在1976/1977年SST躍變前中國汛期降水量在東北地區偏少，華北地區偏多，長江流域偏少，華南偏多，而躍變后則相反。朱益民等[10]指出，PDO位于暖位相期（即中緯度北太平洋異常冷，熱帶中東太平洋異常暖），冬季阿留申低壓增強，蒙古高壓也增強（但東西伯利亞高壓減弱），中國東北、華北、江淮以及長江流域大部分地區降水偏少。針對具體海域對降水的影響，孫柏民等[11]指出，夏季江淮流域降水與1月黑潮區的SST有很好的正相關關系，與6月SST則呈負相關。

中國降水的主要因素有來自印度洋和太平洋受SST驅動的季風和臺風，也有受不同時間尺度的SST和海溫大氣耦合系統的震蕩（如ENSO和PDO等）的影響，過去大多數研究都是以某一具體海域的溫度異常或者局部海域的海氣耦合震蕩來研究對中國降水的影響。本文則以30°E～70°W和50°N～50°S的SST為研究范圍，這也是影響中國降水的季風、臺風以及黑潮的主要來源及活動海域。通過機器學習的方法來挖掘SST對中國降水的時空影響，利用聚焦時延神經網絡（Focused Time-Delay Neural Network，FTDNN）嘗試利用SST對聚類后的中國降水進行中長期的預測。

本文探索通過機器學習的方法建立SST與周降水量的機器學習模型，并用此模型預測各聚類區的周降水量。通過預測的周降水量累加可得到月降水量或季度降水量，從而預測出該區域降水量較長一段時間內的趨勢變化。

2 數據

本文所用的兩個數據集如下：

中國日降水量取自中國地面降水日值0.5°×0.5°格點數據集（V2.0）。該數據集是基于國家氣象信息中心基礎資料專項最新整編的中國地面高密度臺站（2 472個國家級氣象觀測站）的降水資料，利用ANUSPLIN軟件的薄盤樣條法（Thin Plate Spline，TPS）進行空間插值，生成1961年至最新的中國地面水平分辨率0.5°×0.5°的日值降水格點數據。

SST取自NOAA最優插值（Optimal Interpolation，OI）SST每周數據；時間為1981年10月29日—2016年11月13日；SST的選取范圍為30°E～70°W和50°N～50°S，這是影響中國降水的季風、臺風以及黑潮的主要來源及活動海域。

3 研究方法

3.1 降水的時間序列聚類

時間序列是由一組按時間先后順序排列的變量組成，它通常是在相等間隔的時間段內，依照給定的采樣率，對某種觀測要素進行長期觀測得到的[12]。本文將使用K-means聚類算法，選取時間序列的相關性特征將時空立方體的位置劃分為多個簇，每個簇內的時間序列的相關性值較為接近，彼此之間的相似程度高于其他簇中的時間序列[13]。在時間范圍內，統計相關性來衡量時間序列的相似性時，例如，時間序列（1，2，3，4，5）與時間序列（10，20，30，40，50）的值不同，但是完全相關，其差為0，可以通過1減去相關性來計算兩個時間序列之間的差。這意味著完全正相關（相關性=1）的時間序列的差為0，不相關（相關性=0）的時間序列的差為1，而完全負相關（相關性=-1）的時間序列的差為2。所有其他相關程度將生成介于0～2之間的值，正相關性越大表明相似度越高。

本文使用輪廓系數（Silhouette）法確定降水的最佳聚類數。Silhouette系數由Rousseeuw[14]于1987年提出，它能夠衡量一個結點與它屬聚類相較于其他聚類的相似程度，計算方法如下：

式中：a(i)為樣本i到同簇其他樣本的平均距離，a(i)稱為樣本i的簇內不相似度，簇C中所有樣本的a(i)均值稱為簇C的簇不相似度；b(i)為樣本i的簇間不相似度，b(i)值越大，說明樣本i越不屬于其他簇；s(i)接近1，則說明樣本i聚類合理；s(i)接近-1，則說明樣本i更應該分類到另外的簇；若s(i)近似為0，則說明樣本i在兩個簇的邊界上。

3.2 主成分分析降維

主 成 分 分 析（Principal Component Analysis，PCA）可以用于減少特征空間維數、選擇最有用的變量、確定變量的線性組合和識別目標或是異常值分組等[15]。對于一組數據中某個特征組成的多維向量，其中的某些元素本身沒有區分性，比如都為0，或者與0相差很小，那么這個元素本身就沒有區分性，用它做特征來區分，貢獻會非常小。我們的目標是找到變化大的元素，即方差大的那些維，去除掉變化不大的維，從而使特征留下的都是最能代表此元素的值。例如，本文中對于SST在99%的方差被保留之后，SST的數據維度從20 000多個降到600多個。方差太少時無法代表所有的海溫活動，而過大時，會大幅增加輸入神經網絡的維度，增大神經網絡的訓練時間，最終的預測結果也不理想。本文經過測試最終保留了SST均方差為91%的維度來研究主要維度對降水的影響。表1與圖1是本文輸入神經網絡中的前6個主要維度的方差和空間模態。第一模態代表了SST的季節性模態，后5個模態在赤道和太平洋顯示出很大的變化，這些模態捕獲了ENSO、PDO和北太平洋環流振蕩（North Pacific Gyre Oscillation，NPGO）等現象[16]。

表1 前6個主要維度的方差

圖1 SST前6個主要模態的空間分布

3.3 FTDNN

時延神經網絡（Ti me-Delay Neural Network，TDNN）是一種多層人工神經網絡結構，由Waibel等[17]于1989年提出。初衷是為了解決語音識別中，傳統方法隱馬爾科夫模型（Hidden Markov Model，HMM）無法適應語音信號中的動態時域變化。該結構參數較少，進行語音識別不需要預先將音標與音頻在時間線上進行對齊，實驗證明TDNN比HMM表現更好。TDNN的提出具有非常重要的影響，卷積神經網絡（Convolutional Neural Networks，CNN）就是受TDNN影響而發明的，它是卷積網絡的前身。FTDNN神經網絡可以看作是一維的卷積神經網絡，它的共享權重被限制在單一的維度上，且沒有池化層，通過共享權值可以方便學習，在學習過程中不要求對所學的標記進行精確的時間定位，且有能力表達語音特征在時間上的關系，非常適用于語音和時間序列的信號處理[18]。

TDNN與其他神經網絡一樣，由多個由簇組成的互連層進行操作。這些集群意在表示大腦中的神經元，像大腦一樣，每個集群只需要注意輸入的小區域。原典型TDNN具有3層集群，一組用于輸入，一組用于輸出，中間層通過過濾器處理輸入的操作。由于它們的順序性質，TDNN被實現為前饋神經網絡。在TDNN前饋網絡的輸入端帶一個抽頭延遲線，稱為FTDNN。這是動態網絡的一部分，稱為聚焦網絡，其中動態只出現在靜態多層前饋網絡的輸入層。該網絡非常適合時間序列預測，例如混沌激光的測量數據集，該數據集是圣達菲時間序列競賽中使用的數據集，使用FTDNN網絡顯示出很好的預測效果[19]。FTDNN網絡的優點之一是它不需要通過動態反向傳播來計算網絡梯度，這是因為抽頭延遲線只出現在網絡的輸入端，不包含反饋回路或可調參數，因此該網絡比其他動態網絡的訓練速度更快。

本文將日降水數據處理為周降水數據，使之和NOAA的SST產品數據的時間一致，經過K-means聚類得到最佳的聚類結果之后，再將各區域的格點數據取平均。由于降水數據是周數據，原始數據存在一些較大的異常值（見圖2），而異常值的存在會極大地干擾模型訓練，必須對原始數據進行平滑處理。常見的平滑方法有移動平均法、加權平均法和指數平滑法。移動平均法雖然可以很好地過濾掉異常值，但是平滑后的時間序列過于平穩，造成每個分類之間的差異不夠明顯，而加權平均法中合理地分配加權系數較為困難。通常我們認為每周的降水不是一個孤立事件，它不會突然地增大，比如臺風對某地降水的影響。事實上在臺風來臨前的一段時間內，它所影響的區域的降水就會增加，在登陸時增大更加明顯，基于此最后選擇指數平滑算法對原始數據進行平滑。如圖2所示，平滑后的結果降低了異常值的大小，但同時也保留了原始周數據的波動性。

圖2 降水周數據以及平滑后的降水數據

4 結果與討論

4.1 最佳聚類數的確定

基于相關性聚類的輪廓系數值如圖3所示。隨著簇數的增加輪廓系數值也增加，但增長速度放緩，聚類數為7時，輪廓系數值最大。通常輪廓系數值越大聚類效果越好，但聚類數太大時海洋對陸地降水的影響就會分散，聚類數太少時，會使地理空間跨度太大，每個分類的平均值不能很好地代表所包含的時間序列的特征，本文最終選取輪廓系數值最大的7為最終的聚類結果。圖4為基于相關性分7類的聚類結果。從地理分布來看：區域1主要包括東北和內蒙古北部地區，區域2大部分屬于華北和西北東部區域，區域3則屬于西北地區，區域4大部分屬于青藏高原區域，區域5大部分屬于西南區域，區域6大部分屬于長江以南的華東、華中和華南區域，區域7屬于黃河和長江之間的華中和華東區域。從氣候區分布來看，區域1、區域2、區域5、區域6和區域7大部分處于季風區，其降水受季風、臺風和ENSO等海洋活動的影響較大，而區域3與區域4大部分屬于溫帶大陸性氣候和高原山地氣候。本文所分的7個區域分布與中國年降水量分布以及傳統的中國氣候區分布有所差別，這與本文所用的數據是周降水量波動比較大有關，而傳統氣候區在劃分時除了結合氣候區劃分外，還要結合生產實際需要并適當照顧自然區或行政區[20]。

圖3 基于相關性的輪廓系數值

圖4 基于相關性分7類的聚類結果

4.2 聚類特征的可視化

由于降水周數據的數據量比較大，時間序列過長會造成可視化后的數據分布較密集，而每一個簇內包含上百個時間序列，都將其可視化的結果并不理想。為了更好地展示聚類效果和每一個簇的特征分布，選取時間為1993—1998年，空間上使用隨機函數隨機選取5個點的時間序列。

圖5a—c表明相同簇的降水時間序列具有類似的特征，而圖5d與圖6表明不同簇的數據分布有明顯的差別。同一簇具有相同性，而不同簇具有很明顯的差異性，說明聚類結果較為理想。

圖5 分7類時的降水隨時間的變化

圖6 分7類的降水散點圖和小提琴圖

4.3 各區域分析

各區域以訓練集、驗證集和測試集的比例為8∶1∶1輸入數據，通過FTDNN進行訓練，結果如表2所示。隨著運行次數的增加，各區域測試集的最小均方根誤差、相關系數以及全集的最小均方根誤差的最佳延遲時間都穩定在相同的延遲時間。圖7是各區域測試集的平均絕對誤差，從圖7中可以看出，區域1、區域2、區域5、區域6和區域7的平均絕對誤差大于另外兩個區域，這是因為這5個區域的降水主要受季風、臺風和ENSO等海洋活動影響，從而造成周降水值的波動較大。從表2可知，區域1的最佳延遲時間為3周，區域2為4周，區域3為2周，區域4為2周，區域5為5周，區域6為6周，區域7為4周。可見，區域1、區域2、區域5、區域6和區域7等處于季風區區域的最佳延遲時間都比另外兩個處于非季風區的最佳延遲時間大，這可能是由于本文所使用數據的時間分辨率為周，季風區受季風和臺風帶來的降水量比較大導致的。在得到各區域的最佳延遲周后，輸入確定的延遲時間，對各區域單獨進行訓練，圖8與表3是使用各區域訓練得到的模型對各區域2012年7月1日之后11周降水的預測情況。區域6與區域7的預測誤差較大是因為2012年區域7受到臺風帶來的降水的影響，導致該區域降水波動比較大，而對波動較大的信號，通常很難預測準確，區域3與區域4則顯示出很好的預測效果。

圖7 測試集的平均絕對誤差

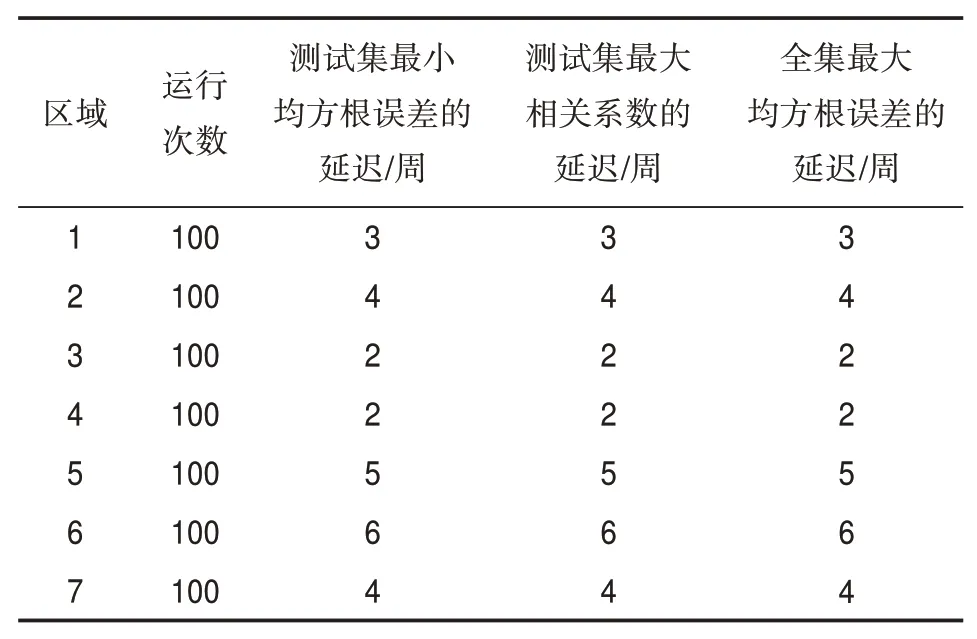
表2 各區域訓練結果

圖8 2012年7月1日之后11周各區域的預測情況

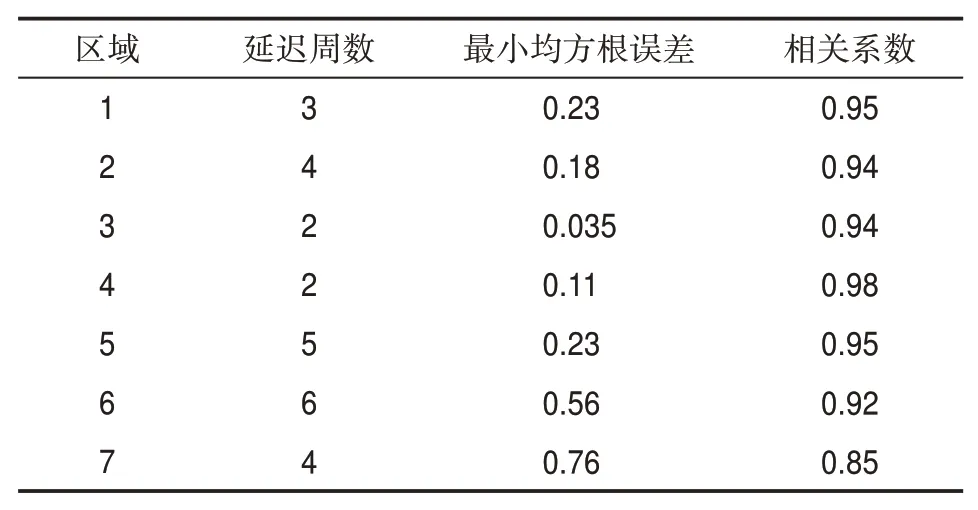
表3 連續11周的各區域模型預測的評價指標

在降水量的中長期趨勢分析上，通過預測的周降水量累加可得月降水量，從而刻畫出該區域降水量較長一段時間內的趨勢變化。這里我們給出了區域6的預測結果。從圖9可知，在大約7.3 a的降水量預測中，月降水量的預測值與真實值的相關系數達0.92，均方根誤差為3.81，較準確地預測了真實降水量的趨勢變化，其他區域的預測情況見表4。與傳統的小波變換重建原序列以及均生函數方法的預測結果相比[22]，本文預測結果的相關系數和均方根誤差都有了很大的提高，例如在新疆地區本文測試結果的相關系數比小波變換結果提高了0.05。

表4 各區域連續88周趨勢預測的評價指標

圖9 區域6連續88 M的預測值與真實值趨勢及相關性

5 結論

本文利用機器學習的方法，以30°E～70°W和50°N～50°S的SST為研究對象，通過K-means聚類算法將36 a的中國周降水數據聚為7個區域，其中區域1、區域2、區域5、區域6和區域7的大部分區域處于季風區，而區域3與區域4的大部分區域屬于溫帶大陸性氣候和高原山地氣候等非季風區。將各區域降水數據經過指數平滑之后輸入FTDNN，并求解其與經過降維處理的SST之間的關系。結果表明，區域1、區域2、區域5、區域6和區域7等受季風和臺風等海洋活動影響較大的區域的最佳延遲時間比遠離海洋區域的最佳延遲時間大，同時也得到了預測各區域降水的最佳延遲時間，其中區域1的最佳延遲時間為3周，區域2為4周，區域3為2周，區域4為2周，區域5為5周，區域6為6周，區域7為4周。在對各區域進行連續11 a的預測中得出，FTDNN神經網絡在利用降維后的SST來預測降水量上顯示出很好的預測效果。

在中長期趨勢預測上，本文的方法也可較準確地預測出某一區域未來降水量的趨勢變化，相比傳統方法預測能力有了較大的提高。但在受海洋活動影響較大區域，短期預測的降水會有很多局部突變值，預測結果不理想，這也是非線性和非平穩信號預測中的難點，以后我們將嘗試將FTDNN結合集合經驗模分解來提高預測效果。