耦合多目標優化和多屬性決策的水庫生態調度方法研究

劉 艷， 李曉春， 羅軍剛

(1.西安理工大學 西北旱區生態水利國家重點實驗室， 陜西 西安 710048；2.陜西省江河水庫管理局， 陜西 西安 710018)

水庫生態調度是在傳統水庫調度的基礎上，將水庫和河道的生態服務功能考慮進來的一種新的調度模式。目前已成為國內外水庫調度領域的研究熱點。在構建生態調度模型時，一般是將生態因子作為約束條件(約束型)或目標函數(目標型)。約束型因其目標函數單一，模型求解較為簡單，而被廣泛應用。Richter等[1]提出了一個評估水庫生態調度的框架，可以用來恢復河道環境流量。Castelletti等[2]為保護河流生態，將最小生態流量作為約束方程加入到水庫調度模型中。Gates等[3]對美國Snake河流上的大壩進行生態調度研究時，通過增加季節性枯水流量，進而提高下游生物棲息地的利用性。梅超等[4]對不同生態流量下的調度方案進行研究，分析了水庫群的綜合效益。范驄驤等[5]建立了一種以魚類產卵棲息地的生態需水為約束條件的生態調度方法。目標型則是將生態因子作為模型的目標函數，因其更符合多目標問題的本質而受到廣泛關注。Halleraker等[6]通過水力-生境模型、IHA指標法、水溫模擬法等多種方法計算環境流量，在此基礎上進行生態調度。尚文繡等[7]通過水文情勢評價指標建立了水庫生態調度模型。朱金峰等[8]研究了供水期末生態調度對生態用水產生的影響。張珮綸等[9]建立了基于需水調控策略的最優供水模型。張召等[10]以天生橋一級水庫為例，建立了以生態保證率為生態目標的優化調度模型。賈磊等[11]構建了能同時滿足生產生活用水和生態需水的水庫調度模型。薛耀東[12]通過對水庫利益主體及其用水特點的分析，構建了面向生態的水庫多利益主體協調調度模型。

目前，水庫生態調度研究一直在不斷進步和完善。但是大部分將生態作為約束條件，不能達到生態目標與其他目標之間的均衡，其次在目標構建時，沒有對目標之間進行定量分析，直接構建模型，對于目標的選擇相對不客觀。因此，本文以林家村水庫為研究對象，在構建模型之前，對各目標之間進行相關分析。為此，本文提出了一種耦合多目標相關分析、多目標優化和多屬性決策的、貫通“建模-求解-優選”全過程的一體化水庫生態調度方法，為水庫生態調度提供一種新的思路和方法。

1 研究區概況

林家村水庫位于陜西省寶雞市以西11 km的渭河峽谷出口處，是一座以農業灌溉為主，兼顧防洪發電和生態供水的水庫，具體所在位置見圖1。年調節水量0.8億m3，為寶雞峽灌區水庫補水1.48億m3，是陜西省重點水利工程。有四個主要部分：主體工程，壩后電站，防護工程和庫區淹沒處理工程。水庫主要特征參數見表1。

表1 林家村水庫主要特征參數

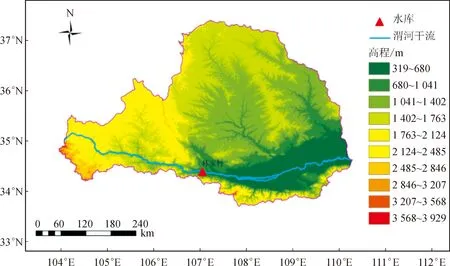
圖1 林家村水庫位置Fig.1 Location of Linjiacun Reservoir

渭水被引入渠道灌溉和發電，有效地緩解了灌區嚴重缺水的情況。但是同時也帶來了生態問題，在枯水期，林家村到魏家堡之間的河道基本處于斷流狀態，并且生態需水滿足率在逐年下降。渭河生態治理進一步增加了對生態用水的需求，使得用水矛盾變得更加突出。因此，為了緩解生態流量不足、保證生態用水需求，開展林家村水庫生態調度是很有必要的。

2 調度目標提取及關系分析

2.1 調度目標提取

生態調度是在兼顧水庫調度的社會、經濟效益的基礎上，重點考慮生態因素的水庫調度模式[13]。為了合理有效地利用水庫水資源，降低不同生態流量指標對水庫經濟效益產生的影響，本文同時考慮灌溉目標、發電目標和生態目標，建立多目標優化的水庫生態調度模型。在構建目標之前，本文對灌溉和發電目標之間進行相關性分析，如果灌溉和發電之間是負相關關系，則建立以灌溉、發電和生態為目標的多目標優化模型；否則，建立以灌溉效益最大、修正全年流量偏差最小為目標函數的優化調度模型。

目標1：灌溉效益最大，可用式(1)表示。

(1)

式中：maxY為最大灌溉效益；Wt為時段灌溉水量；f(Wt)為灌溉水量與灌溉效益的關系。

本文根據文獻[14]的研究成果，在不考慮化肥施用折純量、農業從業人員和農用機械總勞動力變化的情況下，利用面積比擬法，得到寶雞峽塬上灌區灌溉效益與灌溉水量的效益關系如下：

f(Wt)=7.16×Wt0.087

(2)

目標2：發電效益最大，可用式(3)表示。

(3)

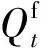
目標3：生態效益最大，即生態AAPFD值最小。采用Ladson等提出的修正全年流量偏差函數(生態AAPFD值)，相關研究表明，生態AAPFD值越小，表示河流生態越好[15]。

(4)

約束條件主要有水位約束、水量平衡約束、出力約束、灌溉需水量約束、機組過流能力約束和渠首引水流量約束等。

2.2 調度目標相關性分析

根據不同典型年(平水年、較枯水年、特枯水年)來水量和灌溉需水量，以文獻[16]中計算的生態流量結果作為約束條件(見表2)。

表2 林家村生態流量Tab.2 Ecological flow of Linjiacun

應用NSGA-II算法[17]求解以灌溉和發電為目標函數的雙目標調度模型，探究灌溉效益與發電效益之間的關系，結果見圖2。從圖2中可以看出，平水年，當發電效益小于0.119億元，發電效益和灌溉效益近似呈線性關系，y1=7.213x+6.684；當發電效益大于0.119億元，灌溉效益y2=7.725，不再隨著發電效益的增加而增加。這是因為灌溉需水量是根據灌溉面積和灌溉定額確定的，不可能是無限大的，當灌溉供水量達到灌溉需水量之后，不會繼續增加，這個時候發電引水只會增加發電效益，對于灌溉效益影響不大。較枯水年和特枯水年發電效益與灌溉效益近似呈線性正相關關系。進一步分析發現，發電效益與灌溉效益平水年的相關系數為0.952，較枯水年為0.991，特枯水年為0.984，三個典型年的發電效益與灌溉效益均在99%置信水平下顯著正相關。

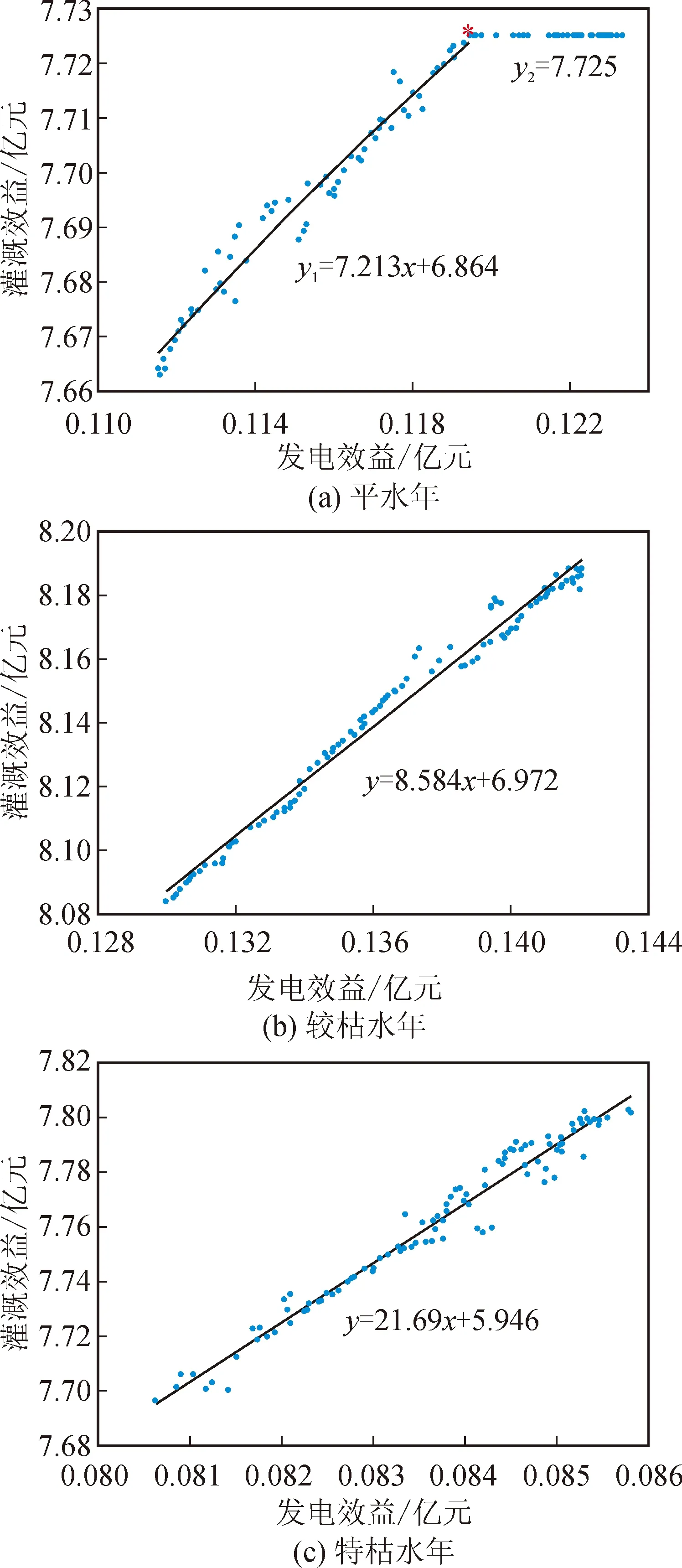
圖2 不同典型年灌溉效益與發電效益關系Fig.2 Relationship between irrigation benefit and power generation benefit in different typical years

為提高水庫的綜合利用效益，有必要進一步分析生態與灌溉、生態與發電目標之間的相互關系。以特枯水年為例，根據文獻[16]中計算的生態流量結果，分別構建灌溉效益最大優化模型，模型目標函數見式(1)；以及發電效益最大優化模型，模型目標函數見式(3)。分別分析計算了生態流量在不同滿足度的條件下，林家村水庫灌溉效益與林家村斷面生態流量的響應關系以及發電效益與生態流量的響應關系。計算結果見圖3。可以看出，隨著生態流量約束的增加，即年生態需水量的增加，灌溉效益逐漸減少且呈近似線性遞減的趨勢。林家村水庫灌溉效益的變化趨勢為：

圖3 年生態需水量與灌溉效益的關系Fig.3 Relationship between annual ecological water demand and irrigation benefits

y灌=-0.0704q+8.1269

(5)

式中：q為生態流量(m3/s)；y灌為灌溉效益(億元)。可以看出，生態流量每增加1m3/s，灌溉效益就減少0.070 4億元。

同樣地由圖4可以看出，發電效益也隨著生態流量約束的增加呈近似線性遞減的趨勢，發電效益的變化趨勢為：

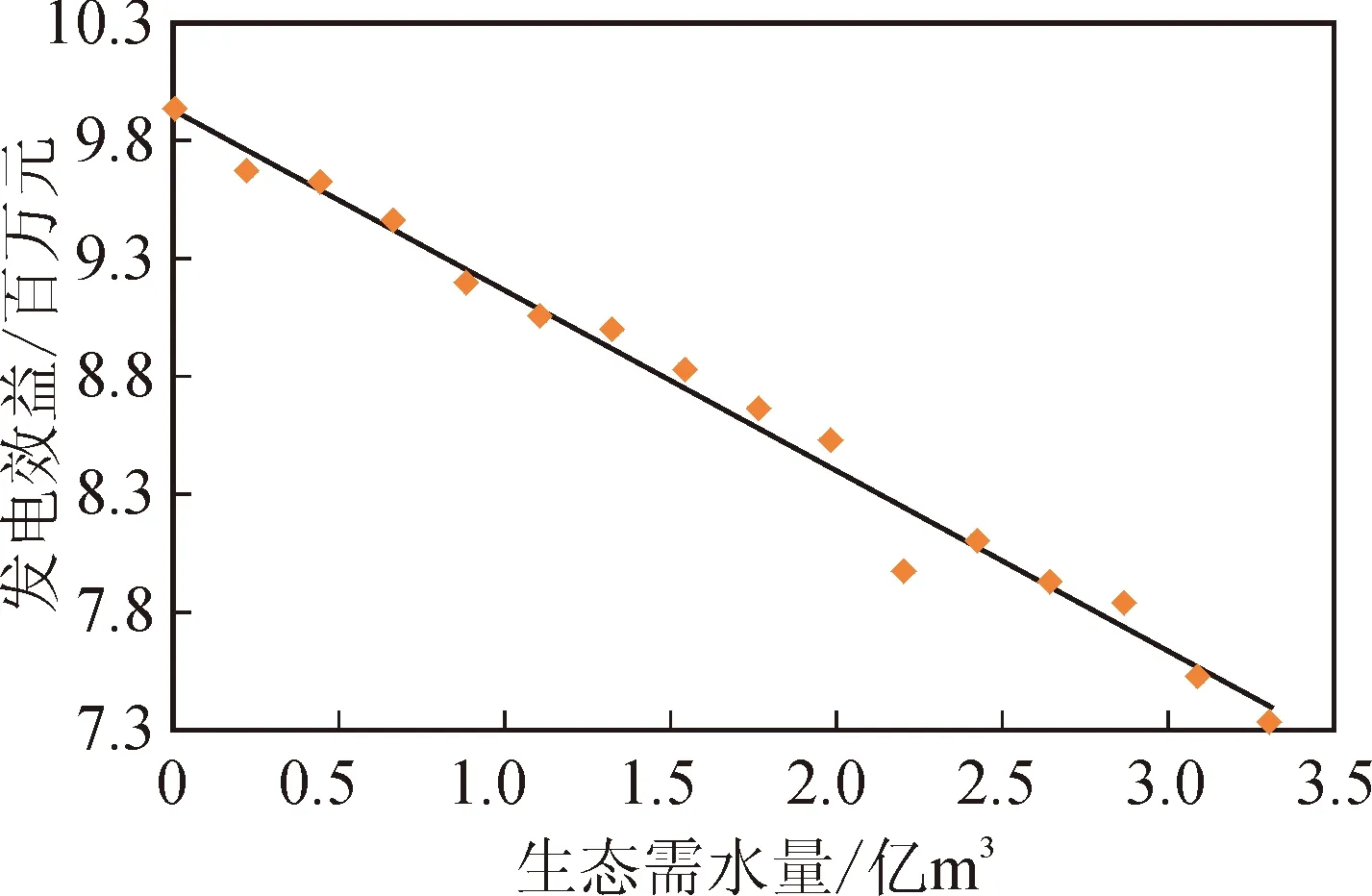
圖4 年生態需水量與發電效益的關系Fig.4 Relationship between annual ecological water demand and power generation benefits

y電=-0.7685q+9.9415

(6)

式中：q為生態流量(m3/s)；y電為發電效益(百萬元)。可以看出，生態流量每增加1 m3/s，發電效益就減少0.768 5百萬元。

通過以上各調度目標之間的相關性分析表明，林家村水庫發電與生態、灌溉與生態之間均存在負相關關系。林家村水庫的發電效益和灌溉效益存在正相關關系，所以一個目標增大的同時，另一個目標也同步增大，反之亦然。因此，在構建目標時，選擇發電效益和灌溉效益這兩個目標其中的一個目標即可。林家村水庫主要是以灌溉用水為首要目標，發電居于次要地位，結合水庫的實際運行情況，由于灌溉放水的不確定性，使得電站無法長期穩定的發電。故本文建立以灌溉效益最大、修正全年流量偏差最小為目標函數，協調建立林家村水庫多目標生態調度模型，并采用平水年、較枯水年、特枯水年3個典型年的徑流資料計算。

3 多目標調度模型構建與求解

3.1 數學模型構建

依據林家村水庫的調度目標之間相關性分析結果，可構建如下的水庫多目標調度模型。

目標函數：

MinimizeF=f(-maxY, minR)，t=1,2,…,T

(7)

約束條件：

1) 水庫水位過程約束:

Zt,min≤Zt≤Zt,max

(8)

2) 時段出力約束:

Nt,min≤Nt≤Nt,max

(9)

3) 機組過流能力約束:

(10)

4) 水量平衡約束:

Vt+1=Vt+(It-Qt)Δt

(11)

5) 灌溉需水量約束:

(12)

6) 渠首引水流量約束:

(13)

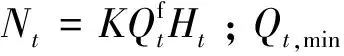
3.2 模型求解算法設計

為解決水庫多目標優化求解-多方案偏好選擇問題，本文將經典的多目標優化算法(NSGA-II)和多屬性決策方法(SEABODE)耦合，建立了一種基于多目標優化-多屬性決策的水庫生態調度模型求解算法(NSGA-II-SEABODE)。該方法的總體思路是：首先，使用NSGA-II算法[17]解決目標優化問題，以獲得備選方案集A；然后，用SEABODE法在方案集A中優選出最終的偏好方案。SEABODE法是一種基于k階p級有效概念的備選方案逐次淘汰法[18]，與傳統方法相比，SEABODE法可直接從決策矩陣中篩選方案，逐步淘汰劣等方案，無需標準化決策矩陣，也無需對屬性權重進行計算，因此，降低了方案在優選過程中受到的主觀影響。NSGA-II-SEABODE算法的求解流程見圖5。

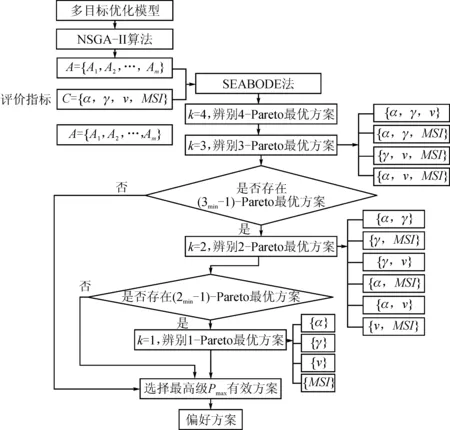
圖5 NSGA-II-SEABODE算法流程圖Fig.5 NSGA-II-SEABODE combined method flow chart

Step1： 利用NSGA-II算法對多目標優化問題進行求解，得到備選方案集A。

Step2： 基于SEABODE法構建四維屬性空間C={α，γ，υ，MSI}對方案集A排序。其中，α為可靠性，γ為可恢復性，ν為脆弱性，MSI為缺水指數。

1) 從k=4開始，在四維屬性空間C={α，γ，υ，MSI}中辨別4-Pareto最優方案，找出所有最低階(記為kmin)。

2) 從選出的四階有效方案集中進一步向三階有效方案進行優選，即k=3，此時三階子空間分別由{α，γ，υ}、{α，γ，MSI}、{γ，υ，MSI}、{α，υ，MSI}構成。

3) 若2)找到的所有kmin-Pareto最優方案中沒有一個是(kmin-1)-Pareto最優的，則選擇的偏好方案為(kmin-1)階最高級(pmax)有效方案。

Step3： 重復3)，直到找出[k,p]-Pareto最優方案為偏好方案。

3.3 生態調度方案合理性評價

基于NSGA-II法對水庫多目標生態調度模型求解，得到含有100個非劣解的非劣解集，為了找尋綜合效益最大的方案，需要對多目標方案進行優選。因此為了進一步淘汰部分較差方案，本文選擇可靠性、可恢復性、脆弱性和缺水指數四個評價指標構成水庫調度合理性評價指標體系的四維屬性空間C={α，γ，υ，MSI},其中α，γ為最大化類型屬性指標；ν和MSI為最小化類型屬性指標。然后，采用SEABODE方法從備選方案集A的100個方案中篩選出最終的偏好方案。

1) 可靠性α。在水庫調度期內，達到需求目標的概率，其計算公式為：

(14)

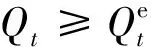
2) 可恢復性γ。在運行分析期內，水庫從破壞狀態恢復到正常供水的平均頻率，其計算公式為：

(15)

式中：γ為水庫供水可恢復性。

3) 缺水深度ν。水庫運行分析期內，單個時段內的最大相對缺水量，其計算公式為：

ν=max{DR1,DR2,…,DRT}

(16)

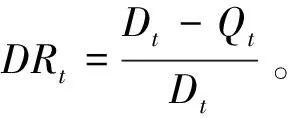
4) 缺水指數MSI。反映水庫供水效益的損失程度。

(17)

式中：T為調度期總時段數。

4 實例計算與分析

4.1 典型年的選擇

選取1950—2018年共69年的水文序列，將其進行排頻計算，然后根據Pearson-Ⅲ型曲線對水庫年平均流量進行適線，選取P=5%為特豐水年，P=25%為較豐水年，P=50%為平水年，P=75%為較枯水年，P=90%為特枯水年。典型年的來水過程見圖6。

圖6 林家村水庫典型年入庫流量Fig.6 Storage water of typical year of Linjiacun Reservoir

4.2 灌溉需水量計算

寶雞峽水庫的主要供水目標包括灌溉、發電和生態用水。根據文獻[19]可知，特豐水年和較豐水年，渠首引水后下泄流量能夠滿足生態流量；平水年引水后生態流量不足；而較枯水年和特枯數年引水前生態基流已不足，引水后更加嚴重。故本文主要計算平水年、較枯水年和特枯水年的灌溉需水量。

根據寶雞峽灌區的灌溉制度和灌溉定額，采用定額指標法，通過分析計算可以得到寶雞峽塬上灌區的月灌溉需水量，結果見圖7。其中50%典型年灌溉需水量為2.43億m3，75%典型年灌溉需水量為5.55億m3，90%典型年灌溉需水量為5.91億m3。

圖7 不同典型年灌溉需水量Fig.7 Irrigation water requirement in different typical years

4.3 優化求解與結果分析

采用MATLAB編制水庫生態調度的NSGA-Ⅱ-SEABODE優化求解算法，以月為調度時段，總調度時段12個，運行期為7月至次年6月。優化問題包括13個決策變量，分別是水庫在12個時間段內的13個水位值(包括起始水位和結束水位)。選取種群規模N=100，最大迭代次數Gen=1 000，NSGA-II算法使用模擬的二進制交叉算子和多項式突變，交叉概率pc=0.9，變異概率pm=1/n，n是決策變量的個數，交叉分配指數ηc和突變分布指數ηm都是20。通過計算可得到100組Pareto最優解。不同典型年的優化調度結果見圖8，可以看出灌溉效益與生態AAPFD值之間存在著競爭關系。為進一步分析優化結果，取其中的兩種典型優化方案：方案1(生態AAPFD值最小)、方案2(灌溉效益最大)。當以追求灌溉效益最大為目標時，可選擇方案2；當追求生態AAPFD值最小為目標時，可選擇方案1。從方案1到方案2，水庫的灌溉效益在增加的同時，生態AAPFD值也在增加。可見為了保障河道內具有一定的生態流量，會使水庫的經濟效益受到一定的影響。

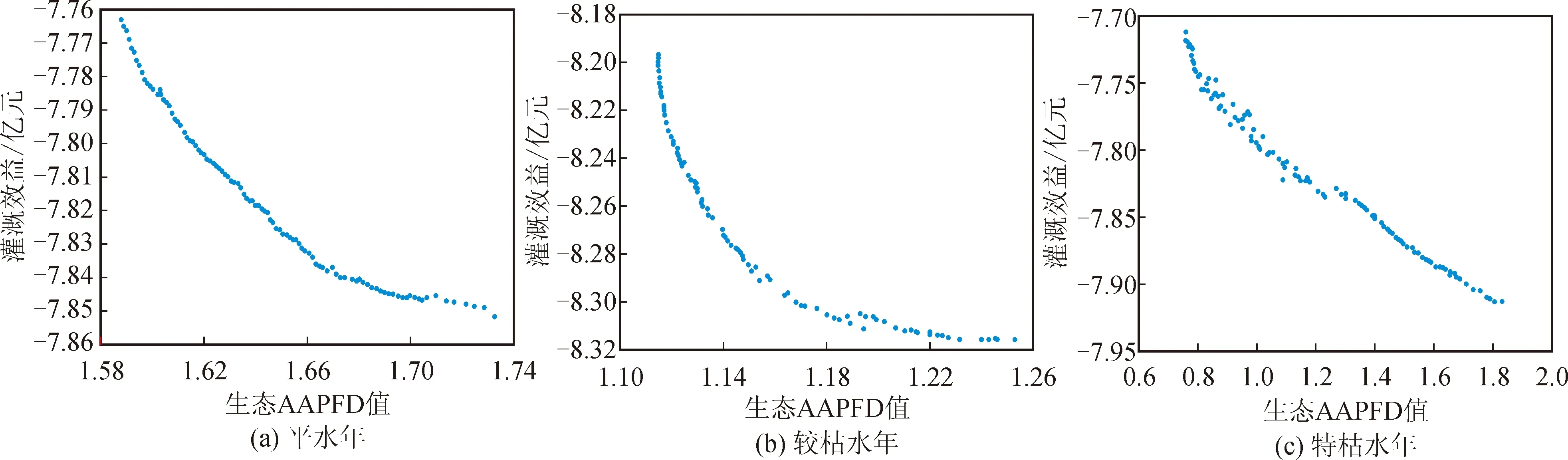
圖8 不同典型年多目標Pareto散點圖Fig.8 Pareto scatter diagram of multi-objective in different typical years

分別計算平水年、較枯水年和特枯水年水庫屬性空間C中4個評價指標值，統計結果見表3。

由表3可以看出，三個不同典型年中，不同方案的4個評價指標均存在差異。

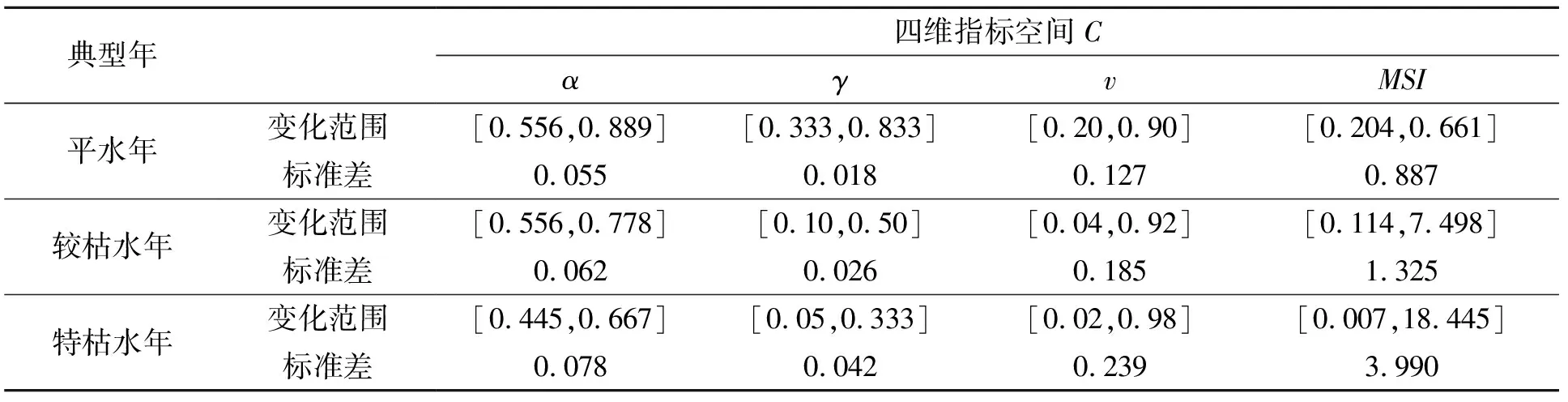
表3 決策空間A中不同典型年評價指標統計結果Tab.3 Statistical results of evaluation indicators of different typical years in decision space A

因此，可采用SEABODE法對方案集進行選擇與淘汰，確定最終的偏好方案。

平水年、較枯水年、特枯水年三種典型年下，四維指標空間C及其三維子空間中的Pareto最優方案數統計結果見表4。

表4 不同典型年的指標空間C中Pareto最優方案個數Tab.4 Number of Pareto optimal schemes in indicator space C of different typical years

表4 不同典型年的指標空間C中Pareto最優方案個數Tab.4 Number of Pareto optimal schemes in indicator space C of different typical years

典型年(1234)(123)(124)(134)(234)三階有效方案平水年4639301887較枯水年564229201513特枯水年49413613129

注：1-α，2-γ，3-ν，4-MSI。

在k=4的第一輪方案優劣排序識別中，不同典型年的方案A1～方案A100，在四維指標空間C中分別有46、56、49個方案是Pareto最優的，相當于偏好方案的優選范圍分別縮小了54%、44%、51%。為了選擇出一個具有代表性的偏好方案，需進一步完善和縮小決策者的選擇范圍。在第二輪中，將所選的四階有效解進一步優化為三階有效解，分別獲得平水年的三階有效方案個數是7個，較枯水年是13個，特枯水年是9個。第三輪k=2的方案優劣排序，同樣使用SEABODE法進行優選，得到了平水年(P=50%)、較枯水年(P=75%)和特枯水年(P=90%)下，多屬性決策的最終偏好方案分別為方案A29、方案A13、方案A80，結果見表5。

表5 典型年偏好方案結果Tab.5 Preference schemes for three typical years

從表5可以看出，不同典型年的生態調度性能評價指標差別很大。平水年的供水可靠性、可恢復性、脆弱性指標均優于較枯水年和特枯水年。其中，較枯水年和特枯水年的調水可靠性α分別下降了12.4 %、24.7%；可恢復性γ分別下降了25.4 %、50.7%；脆弱性ν分別下降了25.0%、33.3%。較枯水年的缺水指數MSI最小，為2.21，表明12月中有2個多月無法滿足正常需水量。平水年、較枯水年、特枯水年的經濟效益分別為7.949、8.452、7.927億元，生態AAPFD值分別為1.624、1.207、1.425。

5 結 論

為解決水庫生態調度模型構建和求解中存在的問題，本文提出并構建了一種耦合多目標相關分析、多目標優化和多屬性決策的水庫生態調度方法，并通過實例分析與驗證可得出如下結論。

1) 通過抽取水庫生態調度目標，并進行相關性分析，從而獲得相互沖突的調度目標，使得水庫生態調度模型的構建更具科學性和定量依據。

2) 將多目標優化和多屬性決策方法結合，構建的NSGA-II-SEABODE算法，能夠在優化求解模型的同時，從Pareto最優調度方案中優選出最終偏好調度方案。

3) 將建模方法、優化算法、優選方法耦合，從而為水庫生態調度提供了一種貫通“模型構建-優化求解-方案優選”全過程的調度方法。