噪聲非高斯條件下基于最大相關熵準則的容積濾波算法

張敬艷，修建娟，董 凱,2

(1.海軍航空大學 信息融合研究所， 山東 煙臺 264000；2.中國電子科學研究院，北京 100041)

1 引言

隨著現代雷達技術的快速發展，多普勒雷達在偵察監視、火力控制等領域得到了廣泛應用[1-2]。多普勒雷達能夠獲得目標相對雷達的徑向速度信息，利用此信息能夠更加精確地跟蹤目標，并為后續火力打擊提供支持。文獻[3]首先處理位置量測，然后利用位置濾波值獲得徑向速度量測的偽線性描述，通過Kalman濾波更新目標的運動狀態。由于不敏Kalman濾波(UKF)即無跡Kalman濾波對非線性不敏感，文獻[4]首先對距離量測和徑向速度量測進行去相關處理，然后通過Kalman濾波和UKF依次處理線性位置量測和非線性徑向速度量測，獲得對目標狀態的估計，并分析了不同的相關系數對估計結果的影響。文獻[5]利用轉換多普勒量測Kalman濾波分別從轉換多普勒量測和轉換位置量測獲得非線性偽狀態估計，并通過靜態最小均方誤差準則融合上述2種估計值，獲得對目標狀態的最終估計。以上方法均采用轉換量測方式進行狀態濾波，由于量測非線性可通過不敏變換等手段進行處理，文獻[6]提出了一種直接不敏卡爾曼濾波算法，并對其性能進行了分析。

上述算法均假設量測噪聲服從高斯分布，但是，在實際應用中，量測噪聲通常是非高斯的[7]，上述算法難以獲得較高的狀態估計精度。雖然粒子濾波能夠較好地解決量測非高斯問題，但是其計算量較大，很難實現對狀態的實時估計[8]。從信息論的角度出發，文獻[9]分析了信息熵在處理非高斯信號時的性質及應用。針對線性非高斯系統，文獻[10]提出了一種最大相關熵Kalman濾波算法，實驗結果表明該算法能夠有效處理量測噪聲非高斯條件下的線性狀態濾波問題。

由于多普勒雷達量測非線性，可考慮利用容積變換[11]近似濾波過程中出現的高斯加權積分；同時，由于量測噪聲非高斯，可利用最大相關熵準則獲取估計誤差的高階矩，從而提高目標狀態估計精度。綜合上述分析，在噪聲非高斯條件下，首先利用容積變換獲得偽量測矩陣，并根據統計誤差線性傳遞模型對量測方程進行近似處理；然后基于最大相關熵準則構造代價函數，并通過固定點迭代更新目標估計狀態，提出了一種基于最大相關熵準則的容積濾波算法MCCKF，仿真實驗驗證了所提MCCKF的有效性。

2 最大相關熵準則

兩個隨機變量之間的廣義相似性可以用相關熵進行度量[10,12]。給定2個隨機變量X,Y∈R，其聯合概率分布函數為FXY(x,y)，那么二者之間的相關熵可以定義為：

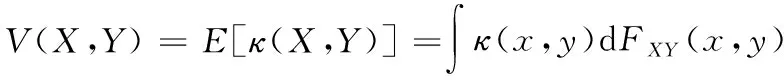
(1)

其中，E表示期望，κ(·,·)表示移位不變Mercer核函數。本文采用高斯核函數進行相關計算，即

(2)

其中：σ>0表示高斯核帶寬。對式(2)所示的高斯核函數κ(x,y)進行泰勒展開，并代入式(1)，得到

(3)

從式(3)可以看出：相關熵是誤差X-Y偶數階矩的加權和。在核帶寬σ足夠大的情況下，相關熵的大小將由二階矩決定。

在實際應用中，聯合概率分布函數為FXY(x,y)通常未知，只能得到有限的采樣數據集合{x,y}。此時，可利用樣本平均估計相關熵，即

(4)

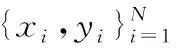
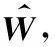
(5)

3 問題描述

考慮二維空間中的勻速直線運動目標，其動態方程為

xk+1=Fkxk+wk

(6)

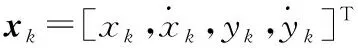
利用多普勒雷達觀測目標的運動狀態，對應的量測方程為

zk+1=h(xk+1)+vk+1

(7)

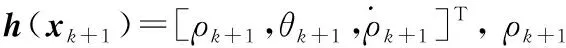
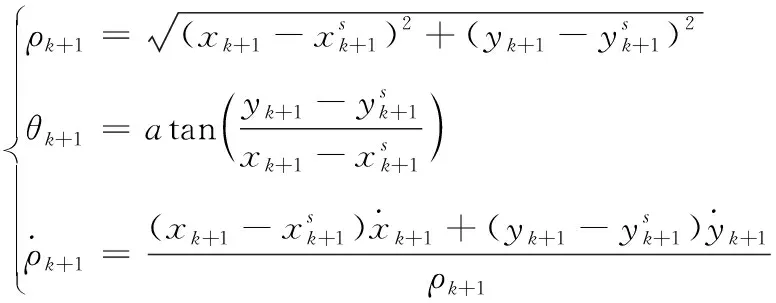
(8)

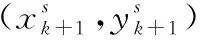
(9)

4 MCCKF算法推導

本節將最大相關熵準則與統計線性回歸模型結合，推導了一種用于解決非線性非高斯系統狀態濾波的新方法。與最小均方誤差估計不同，相關熵考慮了誤差的二階及更高階矩。因而，在閃爍噪聲這類長拖尾非高斯噪聲條件下，基于最大相關熵準則能夠獲得相對更好的狀態估計性能，仿真實驗部分對此進行了驗證，此處不再贅述。與CKF等Kalman類濾波器相似，MCCKF也分為時間更新與量測更新兩部分，具體如下：

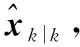
(10)

(11)

根據容積求積分規則，對預測協方差Pk+1|k進行Cholesky分解，獲得相應的狀態采樣點

(12)

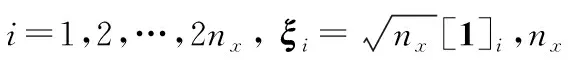
(13)

經量測函數h(·)傳遞后的容積采樣點為

Zi,k+1|k=h(χi,k+1|k)

(14)

量測的一步預測值可以表示為

(15)

進一步，狀態-量測交叉協方差可以表示為

(16)

因此，偽量測矩陣Hk+1可以表示為

(17)

根據統計誤差線性傳遞模型，量測方程(7)可以表示為

(18)

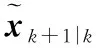
(19)

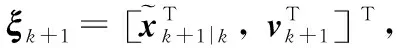
(20)

dk+1=Wk+1xk+1+ek+1

(21)

其中，

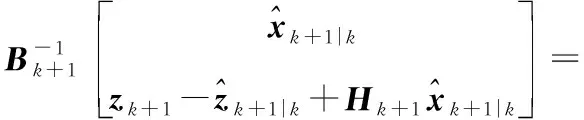
(22)

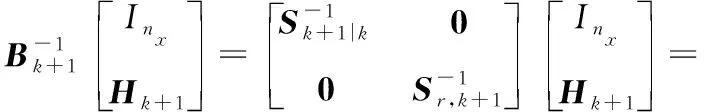
(23)

(24)

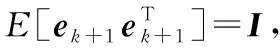
(25)

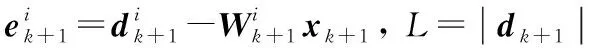
(26)

對JL(xk+1)求導數，并令

可以得到

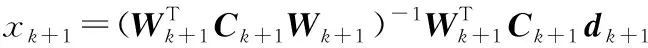
其中，

將式(22)和式(23)代入式(27)，得到

(28)

(29)

利用矩陣求逆引理，并將式(28)和式(29)代入式(27)，得到

(30)

其中，

(31)

(32)

對應的估計誤差協方差可以表示為

(33)

從式(21)、式(27)和式(30)可以看出，式(30)實際上是一個關于xk+1的固定點方程，即

xk+1=g(xk+1)

(34)

因此，可利用固定點迭代算法獲得式的解，即

(35)

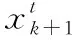
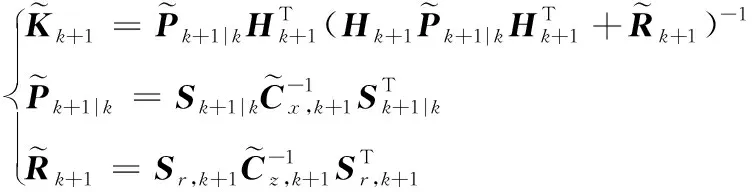
(36)

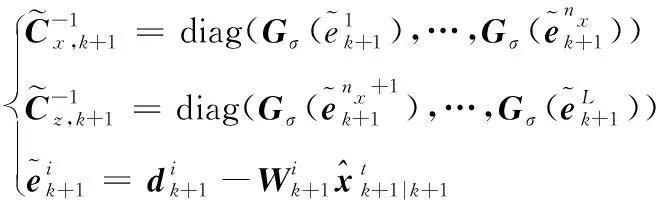
(37)

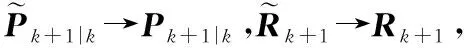
綜上所述，通過引入最大相關熵準則，并利用固定點迭代更新目標的狀態估值，MMCKF可有效捕獲量測中的非高斯噪聲信息，實現濾波性能的提升，仿真實驗對此進行了驗證。MCCKF算法的具體流程如下：

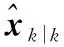
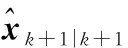
(2) 利用式(12)～式(17)計算偽量測矩陣Hk+1，并構造式所示的統計誤差線性傳遞方程；

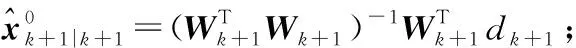
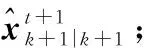
則執行步驟(6)；反之，則繼續執行步驟(4)，直至前后兩次迭代估計值滿足上述收斂條件。

(6) 更新估計誤差協方差

5 仿真實驗

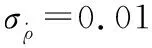
5.1 高斯量測噪聲

假設量測噪聲服從高斯分布，即vk+1～N(0,Rk+1)，得到各算法的估計結果如下：

從圖1和圖2可以看出：在高斯噪聲條件下，EKF、UKF和CKF的估計誤差相對較小，而所提MCCKF的估計誤差相對較大。此外，隨著高斯核帶寬σ的增加，所提MCCKF算法逐漸逼近CKF等的狀態估計性能。從圖 3可以看出：UKF和CKF的狀態估計一致性相對較高，而EKF、MCCKF類算法的估計一致性相對較差。

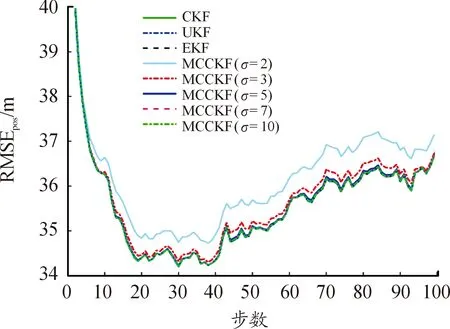
圖1 位置均方根誤差曲線

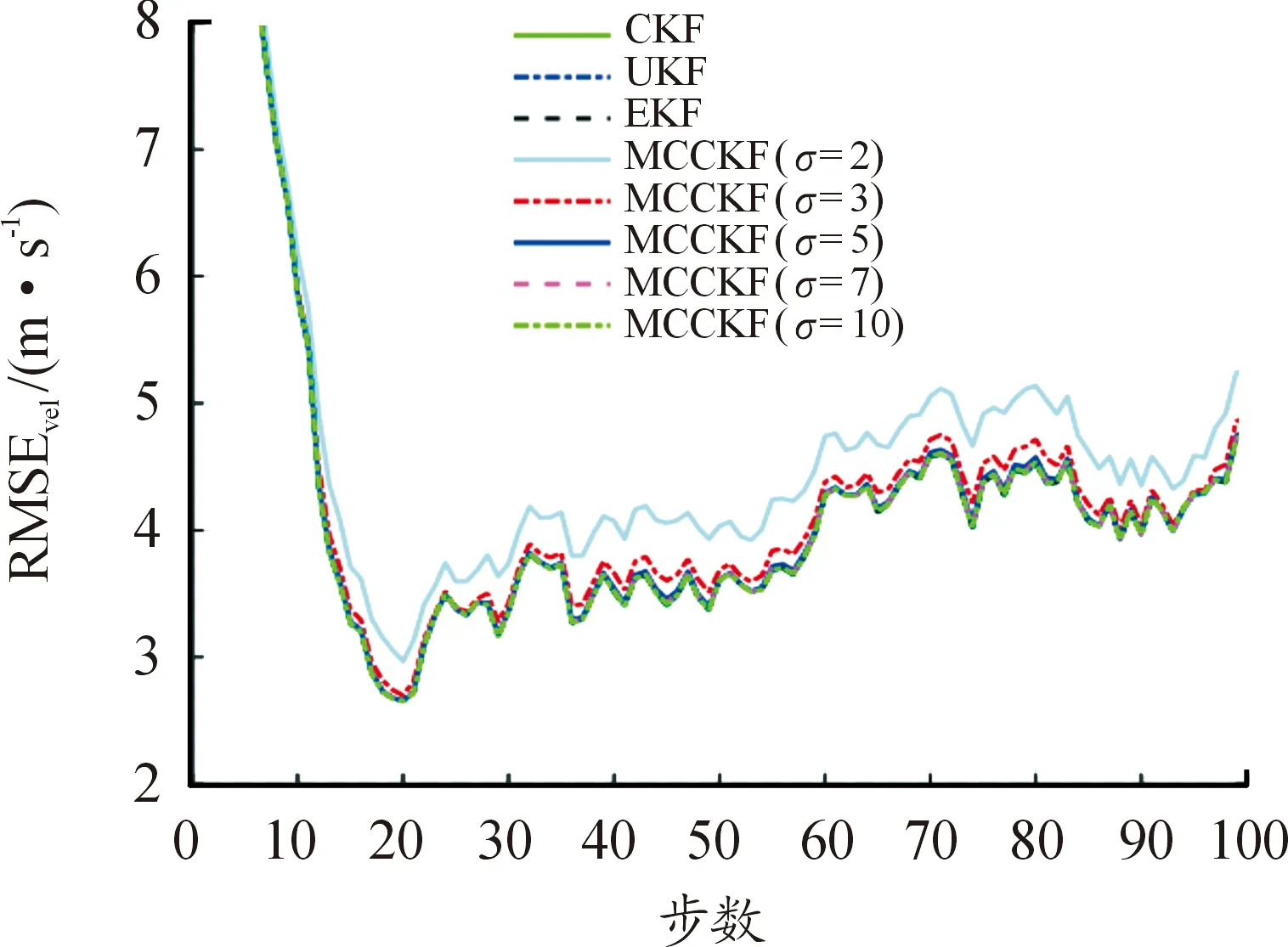
圖2 速度均方根誤差曲線

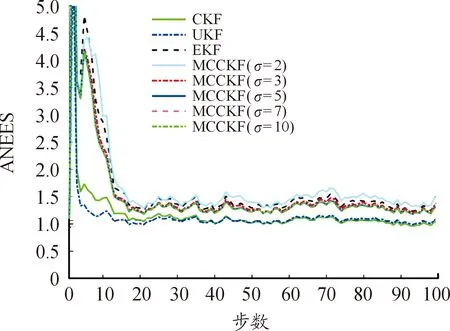
圖3 平均歸一化估計誤差平方曲線

進一步，從表1可以看出：經過少量的迭代，所提MCCKF算法便可實現收斂。從表2可以看出：隨著高斯核帶寬σ的增加，MCCKF的估計誤差逐漸減小，并逼近CKF等的估計結果。

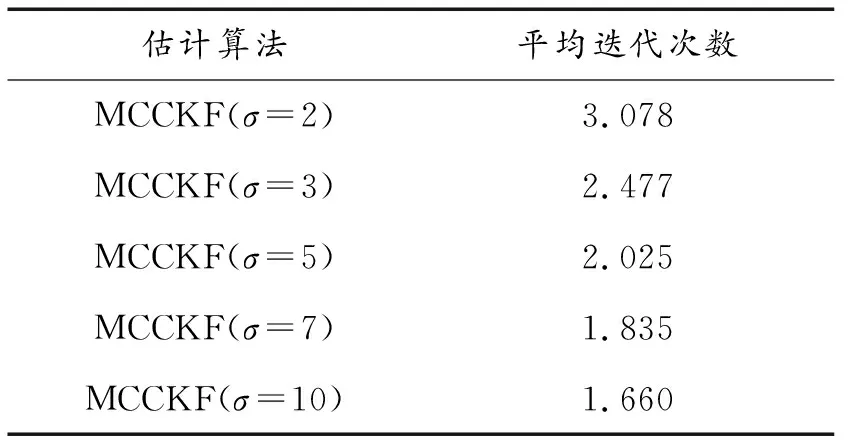
表1 平均迭代次數隨帶寬σ的變化

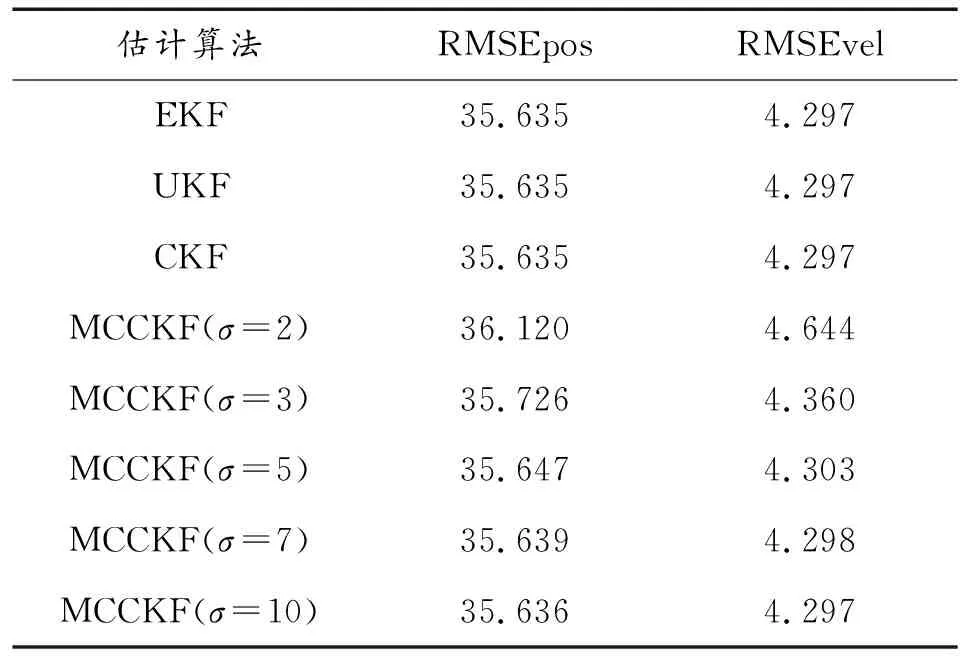
表2 高斯噪聲條件下的估計誤差

5.2 非高斯量測噪聲

假設量測噪聲服從非高斯分布，即vk+1∶0.95N(0,Rk+1)+0.05N(0,50Rk+1)，得到各算法的估計結果如圖4～圖6所示。

從圖4可以看出，在非高斯噪聲環境下，與CKF等Bayes估計相比，MCCKF算法的位置估計誤差相對較小，且在σ=2時估計誤差最小。與圖4所示的結果相似，在圖5中，除少數時刻外，MCCKF算法的速度估計誤差較CKF等Bayes估計小。從估計一致性來看，圖6所示的結果表明：從k=20開始，MCCKF算法的ANEES基本落在置信區間內，而CKF等大部分時刻落在置信上界上方。因此，MCCKF算法的估計一致性相對較好。

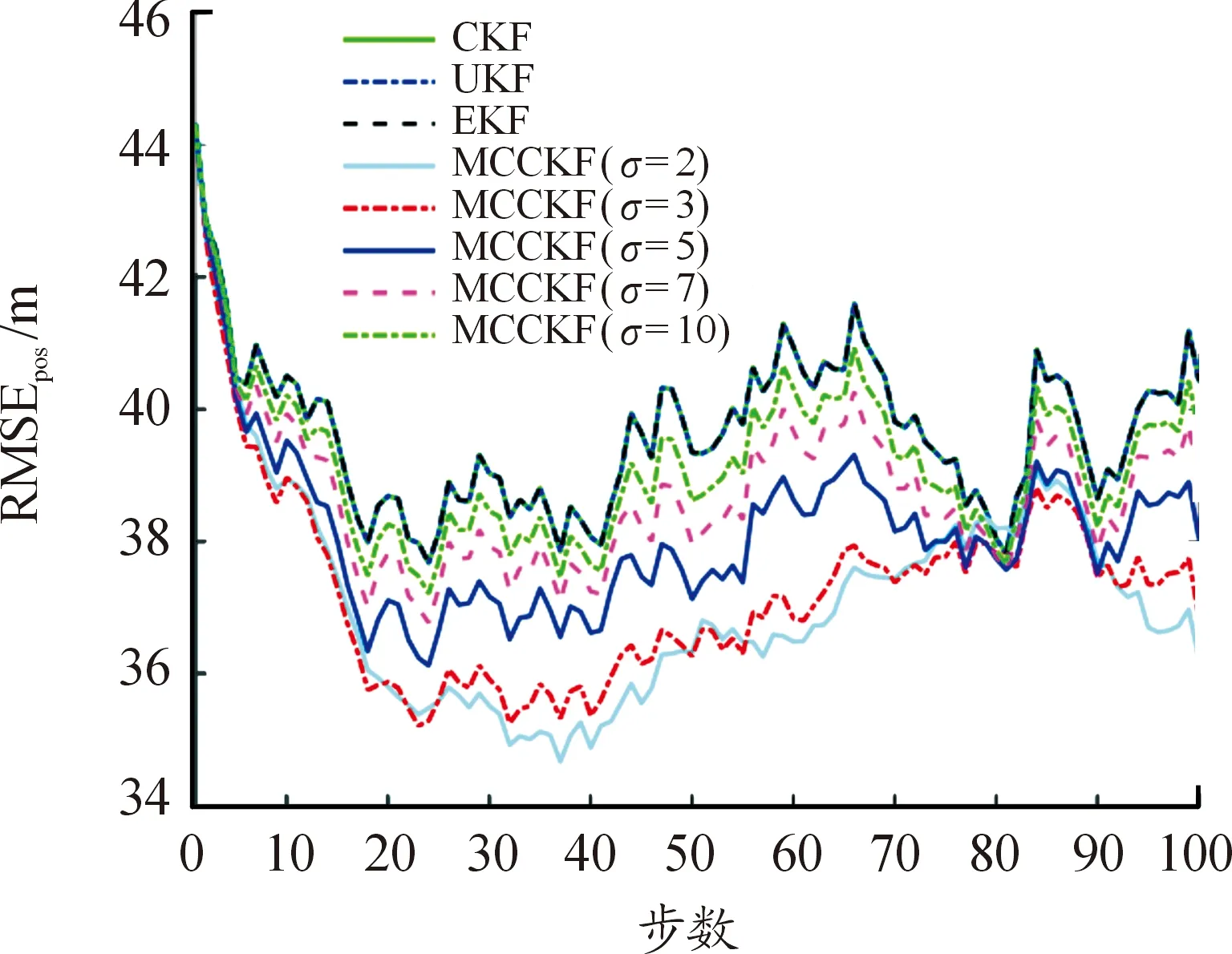
圖4 位置均方根誤差曲線

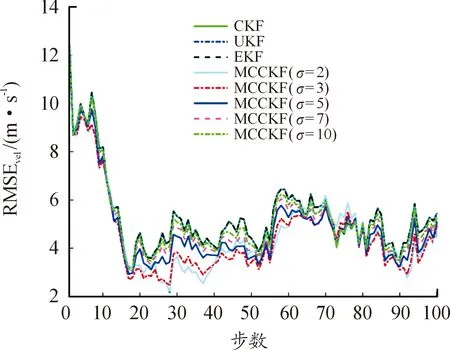
圖5 速度均方根誤差曲線

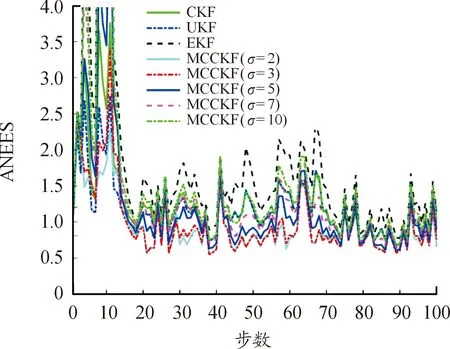
圖6 平均歸一化估計誤差平方曲線

進一步，表3比較了平均迭代次數與核帶寬σ的關系，結果表明：經過少量的迭代，MCCKF便可實現收斂，從而不會造成計算量的大幅增加。表4比較了各算法的平均位置和速度估計誤差，可以看出，MCCKF的位置和速度估計誤差相對較小，且隨著高斯核帶寬σ的減小，估計誤差也逐漸減小，與高斯環境下的結果相反。因此，在高斯噪聲環境下，為獲得良好的狀態估計結果，應選擇較大的核帶寬σ，而在非高斯噪聲環境下，應選擇較小的核帶寬σ，以捕獲誤差的高階矩信息，從而實現對目標狀態的高精度估計。

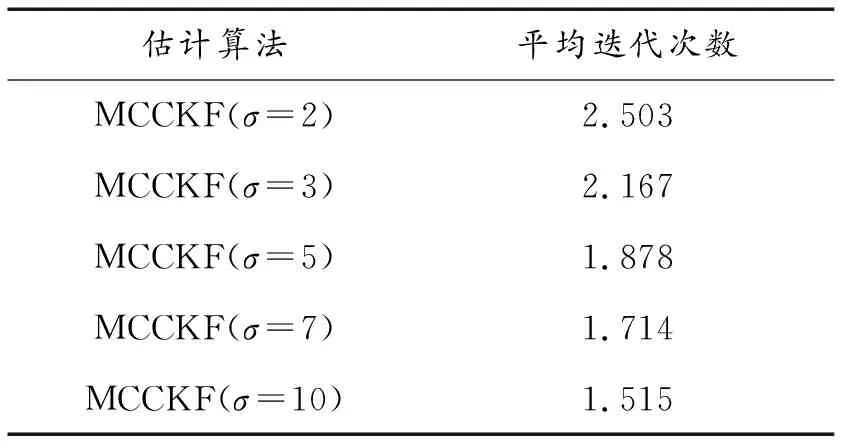
表3 平均迭代次數與帶寬σ的關系

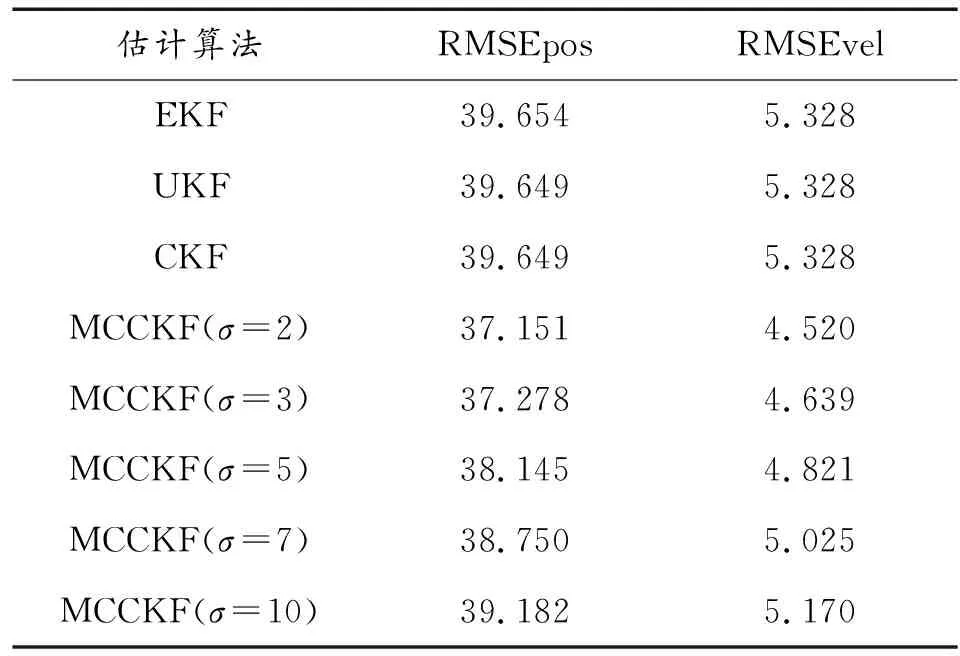
表4 非高斯噪聲條件下的估計誤差

所提方法考慮了估計誤差的高階矩，的確帶來了計算成本的增加，從而造成計算量比CKF大。但是，實驗結果證明：經過少量(大約2次)固定點迭代，所提算法便可實現收斂，并且獲得相對較高的估計精度。因此，與CKF算法(不需要固定點迭代)相比，計算成本不會顯著增加。論文針對所提MCCKF算法在不同高斯核帶寬條件下的迭代次數進行了比較，隨著高斯核帶寬的增加，收斂所需迭代次數逐漸減少，并不是說算法的迭代次數比已有算法更少了。

6 結論

針對艦載多普勒雷達在非高斯量測噪聲環境下的非線性狀態濾波問題，基于最大相關熵準則和固定點迭代更新策略，提出了一種基于最大相關熵準則的容積濾波算法MCCKF。仿真結果表明：在量測噪聲非高斯條件下，經過少量的固定點迭代，MCCKF能夠獲得較已有CKF等Bayes方法更高精度的狀態估計結果，為解決多普勒雷達非線性非高斯狀態濾波提供了一種新的解決思路。