基于雷達海雜波的蒸發波導GA-PSO算法

張 瑜，周文靜，邢孟女

(河南師范大學 物理與電子工程學院， 河南 新鄉 453007)

1 引言

海上大氣環境中經常會出現大氣波導現象，是由于海面水汽蒸發、海洋邊界層大氣的溫度和濕度隨高度急劇變化造成的[1]。蒸發波導屬于一種特殊的表面波導，容易影響無線電波傳播[2]。蒸發波導主要發生在海面40 m以下的范圍內，出現的概率可達80%，因此加強蒸發波導的研究對提高雷達探測精度及雷達整體性能具有非常重要的戰略意義[3]。

早期蒸發波導的研究出現了波導模理論、幾何光學理論和拋物方程方法等基礎理論。在這些理論基礎上，深入研究氣象條件對大氣環境下電波傳播的影響，例如湍流、散射等現象對電磁波傳播方向和距離的影響。通過利用海面上的一些氣象水文因素，如風速、位溫、比濕，建立波導模型可以得到大氣波導的剖面。美國的Paulus-Jeske提出了PJ模型，用不隨氣壓變化的位折射率替代折射率N，利用總體理查森數判斷大氣穩定度來計算不同穩定度條件下的蒸發波導高度[4-5]。法國的研究者依據莫寧-奧布霍夫相似理論提出了MGB模型，可以對穩定和不穩定情況進行迭代解析，該模型根據大氣折射率與氣壓、溫度、水汽壓的關系，比濕與水汽壓的關系，位溫和氣溫的關系，采用Geleyn方法建立模型[6]。美國學者Babin通過研究海洋大氣邊界層物理過程描述模型，把飽和水汽壓公式融入其中；將相似理論用到低風速環境并確定相似理論中的參數，由此得到計算海面蒸發波導高度的模型[7]。美國的Naval Surface Warfare Center在弗吉尼亞Wallops島進行實驗研究[8]，發現雷達回波的變化與大氣折射率的變化有關，利用雷達海雜波數據對大氣波導參數進行反演，可實時提供蒸發波導信息[9]。在這之后的諸多研究都是基于該實驗展開的，如遺傳算法[10]、濾波算法[11]、蟻群算法[12]、免疫算法[13-14]、粒子群算法[15]等相繼被用于計算反演模型。海軍工程大學的左雷也曾將整體理查森數Rib引入蒸發波導剖面模型，利用不同Rib求出不同的折射率剖面[16]。

由于雷達接收的海雜波和蒸發波導參數之間的關系為非線性，因此在這些利用雷達海雜波反演蒸發波導的大多數方法中，其反演精度受到了很大的限制。為此，本文利用增加約束條件的手段來提高反演精度，提出了一種基于不同天線高度、多波段雷達頻率的多目標遺傳—粒子群(GA-PSO)混合算法，以期望得到高精度和高穩定性的反演結果。

2 基于雷達海雜波的蒸發波導反演方法

2.1 雷達海雜波功率計算模型

蒸發波導模型在雷達海雜波反演過程中起著非常重要的作用，通常采用大氣修正折射率M進行大氣波導環境分析。假設理想狀態大氣和海面溫度不變，則修正折射率與觀測高度之間的關系式為

(1)

該模型將蒸發波導厚度d作為特征參數，因其與實際情況吻合度高而應用廣泛。其中z為高度；z0為波導底層高度，取值1.5×10-4；M0為距海面z0處的大氣折射率，取值340。

根據建立的蒸發波導參數模型，可利用雷達方程得到雷達海雜波功率的函數表達式為

Pc(m,r)=-2L(m,r)+10log10r+σ0+C

(2)

Pc是關于大氣波導特征參數m的函數式，這里的大氣波導參數即為蒸發波導厚度d。其中r為雷達到海面的距離；C為與雷達系統參數有關的常數；σ0為海雜波散射系數，由雷達海雜波估計模型GIT求得。

理論研究表明[17]：影響接收雷達海雜波功率的因素有很多，如雷達頻率、雷達增益、天線架設高度、極化方式、海況等，其中影響最大且可控的因素是雷達頻率和天線架設高度。在蒸發波導高度較低時，高的雷達頻率具有較好的反演精度；反之，蒸發波導高度較高時，低的雷達頻率具有較好的反演精度。另外，不同的雷達天線高度含有不同的海雜波特征信息，它與反演精度之間并非單調變化影響，在雷達頻率一定時，總存在某一天線高度使得反演誤差最小。

2.2 目標函數的建立

目標函數可用來判斷實測海雜波回波功率和建模仿真所得海雜波回波功率之間的符合程度。在利用海雜波反演蒸發波導時，當雷達的頻率和天線高度固定時，可建立單目標函數[18]。這種情況下，由于雷達的頻率和蒸發波導高度很難達到匹配狀態，因此反演得到的蒸發波導的精度較差。為了提高反演精度，采用變化雷達頻率的方法，即采用多波段雷達頻率測量海雜波來反演蒸發波導，建立多目標函數。這樣就可以在蒸發波導高度未知的情況下，減小雷達頻率造成的誤差，提高反演精度。另外，在雷達多頻率探測的基礎上，采用調節天線高度獲得豐富的海雜波特征信息，進一步提高反演精度。

蒸發波導環境下，雷達海雜波反演大氣折射率剖面的實現步驟如下：

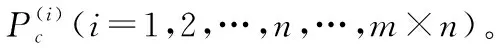
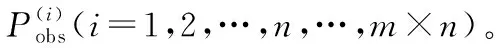
3) 建立關于實測雜波功率和建模所得雜波功率庫之間的目標函數，這里采用均方誤差和線性加權來描述目標函數。表達式為

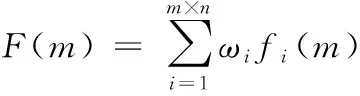
(3)

(4)

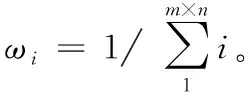
本文選取頻率個數為2，f1=10 GHz，f2=12 GHz，天線高度個數為3，h1=10 m，h2=20 m，h3=30 m。不同的頻率與不同的天線高度相結合會影響反演精度，可通過各種組合對單目標函數與多目標函數進行誤差分析。

2.3 利用GA-PSO混合算法求解目標函數

GA-PSO混合算法是將遺傳算法與粒子群算法進行結合，既留下了遺傳算法的全局搜索優勢，還加入了粒子群的種群信息和位置轉移能力。

多目標GA-PSO混合算法是將多波段頻率和多個天線高度組成的目標函數作為反演對象，采用遺傳-粒子群混合算法進行反演，可求得目標函數取得最小值時所對應的蒸發波導高度。多目標GA-PSO混合算法將遺傳算法嵌入到粒子群的位置和速度迭代更新中，先進行遺傳算法優化，得到一組搜索值后再進行粒子群算法優化，通過設置位置參數，來選擇實際需要搜索的數據范圍。該算法全局搜索能力強，反演結果精確度高，穩定性好。

混合算法主要需要3個算子：提高算子、選擇交叉算子、變異算子。在遺傳算法中個體被看作染色體，在粒子群算法中個體被當作粒子，群體中優秀個體被選拔出來組成一個新群體，另外一部分則被淘汰掉；新群體經過選擇交叉后留下子代優秀個體，最終經過變異算子后的子代和優秀個體組成的新群體進行下一代的選拔。

適應度函數即為評價函數，是遺傳算法中個體是否優秀的評判標準。多目標GA-PSO混合算法保留了遺傳算法這一特點，需要確定適應度函數，對群體中的所有個體進行適應度比較。由于在任何情況下適應度函數都應是非負值，本文所建立的目標函數F(x)滿足該要求，將其倒數作為適應度函數進行算法反演，以便得到目標函數最小值。

算法的實現流程如圖1所示。

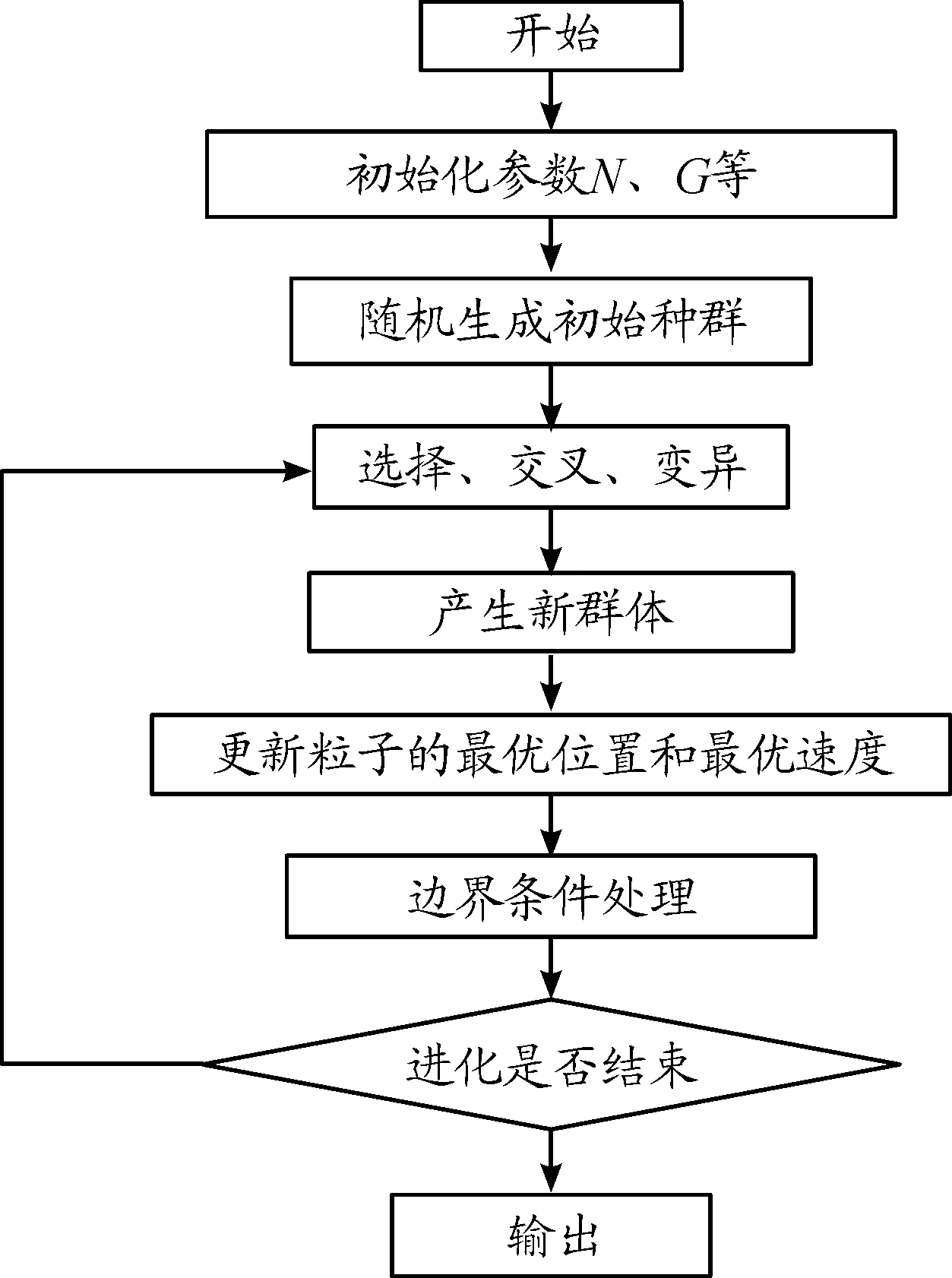
圖1 多目標GA-PSO算法流程框圖

多目標GA-PSO混合算法的具體操作步驟如下：

1) 初始化種群個數N，迭代次數G，慣性權重，學習因子，設置位置參數范圍和速度范圍。

2)隨機生成粒子的初始位置x(i)和速度v(i)，設置適應度函數。

3) 引入遺傳算法，依次進行選擇、交叉、變異。

4) 計算局部最優值和全局最優值，留下最優個體的位置和速度。

5) 邊界條件處理。

6) 循環步驟3)、4)、5)，最后輸出最優解。

3 仿真結果分析

本文通過仿真實驗分析來驗證多波段且可調節天線高度的雷達系統利用多目標GA-PSO混合算法可以對蒸發波導反演精度產生影響。實驗設置初始種群個數N=50，反演代數G=30，計算機配置為4 GB內存，CPU主頻2.60 GHz，雷達環境參數如表1所示。

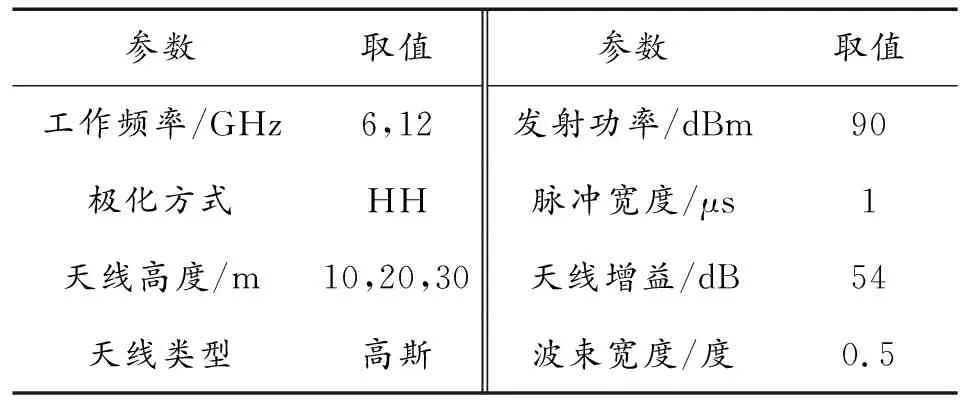
表1 雷達環境參數

在假定蒸發波導高度d為15 m、20 m兩種情況下進行模擬仿真實驗。圖2和圖3分別給出了仿真實驗所得蒸發波導高度d為15 m、20 m時目標函數值隨進化代數變化的優化曲線。兩圖從上到下分別為天線高度h1、h2、h3和可調節高度(h1,h2,h3)，從左到右分別為雷達頻率f1、f2和兩組合頻率(f1,f2)，可以看出隨著反演代數的增加，目標函數逐漸尋得最小值。

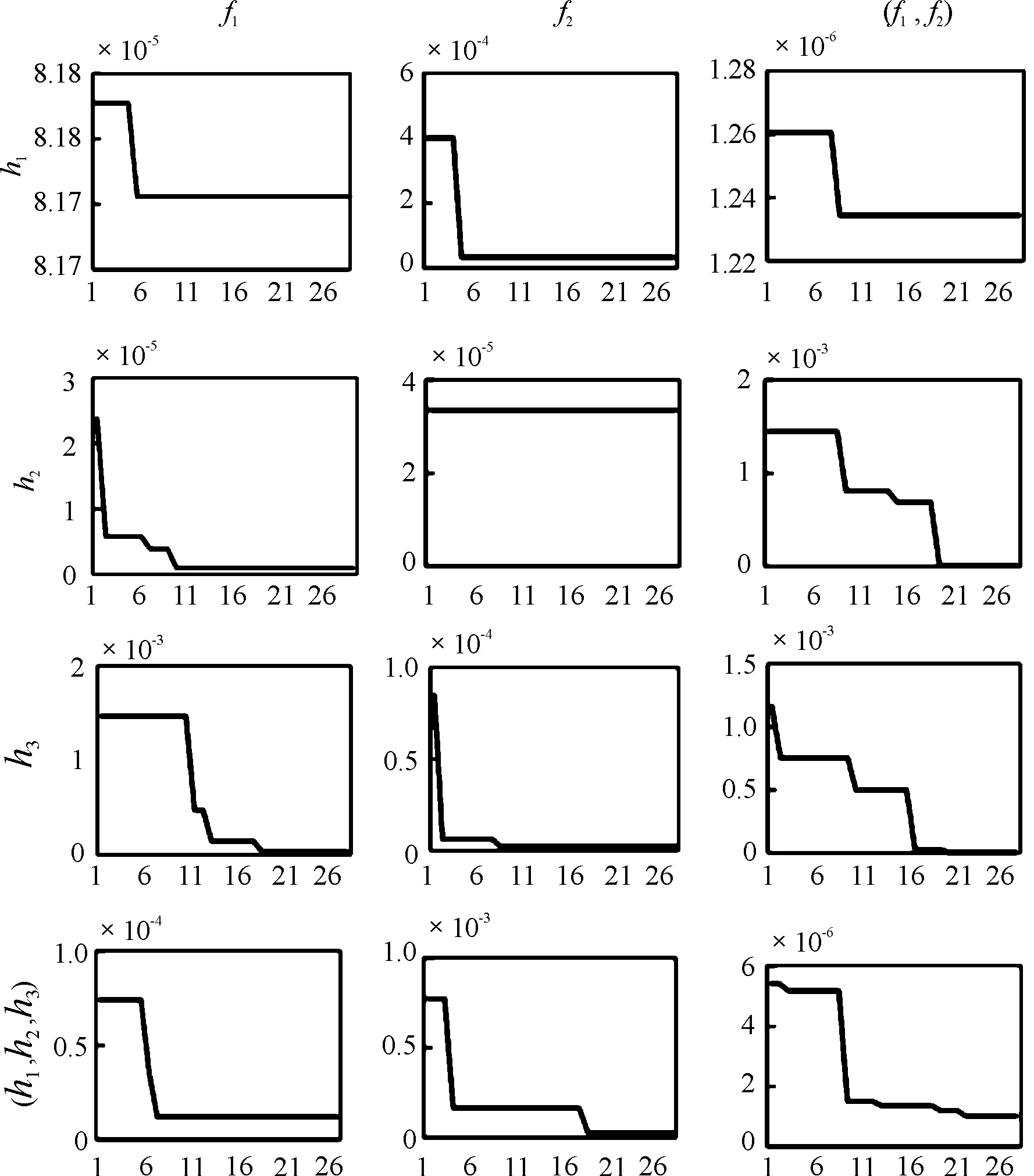
圖2 波導高度為15 m，不同頻率、天線高度下的目標函數優化曲線

目標函數均方誤差值如表2所示。由表2可見：在波導高度為d=15 m時，當雷達頻率為f1=10 GHz、天線高度為h2=20 m，雷達頻率為雙頻率(f1,f2)、天線高度為可調節這2種情況下，目標函數均方誤差值都很小。在波導高度為d=20 m時，只有雷達頻率為f2=12 GHz、天線高度為可調節情況，其目標函數均方誤差值很小。綜合2種波導高度環境，雙雷達頻率(f1,f2)、天線高度可調節情況下的目標函數均方誤差值都較小。

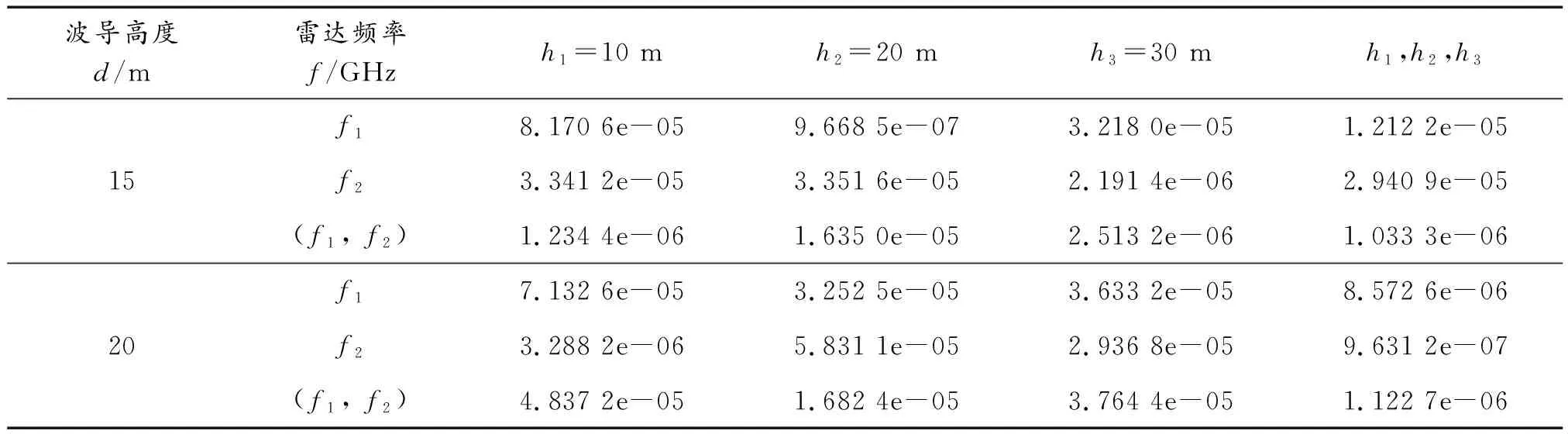
表2 目標函數均方誤差值

在假定波導高度分別為15 m、20 m時，反演所得蒸發波導高度以及其相對誤差如表3所示。

表3 蒸發波導反演高度與其相對誤差

由表3中數據可得：在波導高度為d=15 m時，只有頻率f1=12 GHz、天線高度h2=20 m的反演蒸發波導高度誤差比雙頻率、天線高度可調節情況下的值小，其他情況均比雙頻率、高度可調節情況的反演結果差。在波導高度為d=20 m時，頻率f1=10 GHz、天線高度可調節與雙頻率、高度可調節情況下的蒸發波導反演高度的相對誤差值相等，其他情況下都比雙頻率、高度可調節情況下蒸發波導反演高度的相對誤差值大。由此可見，除了在某種特定情況下，單雷達頻率、單天線高度、所要測量的蒸發波導高度相匹配時，具有很高的蒸發波導反演精度外，其他情況下均具有較大誤差。采用雙雷達頻率、可調節天線高度方法在一般情況下均可提高蒸發波導的反演精度。可以預測，當采用多頻段雷達，更多可調節天線高度參數時，可使得反演蒸發波導參數的精度更高。

4 結論

1) 利用大氣波導效應實現雷達超視距探測的關鍵是獲得精確的波導特征參數，而利用雷達海雜波反演蒸發波導是獲得波導特征信息的有效方法。

2) 利用GA-PSO混合算法對雷達單、多頻率，雷達天線固定、可調節等不同情況進行蒸發波導反演剖面的仿真實驗，結果表明對多個雷達頻率和可調節天線高度的反演剖面更接近實測剖面。

3) 本文提出的基于不同天線高度、多波段雷達頻率反演蒸發波導特征信息的遺傳-粒子群混合算法可提高蒸發波導反演精度和算法穩定性，具有實際應用意義。