多頻帶帶寬相參合成技術研究現狀

張 碩，楊 君，葛鵬程，馮婷婷，杜 鈺

(航天工程大學， 北京 101400)

1 引言

在空間作戰、空間態勢感知等軍事應用中，需要借助雷達對目標的高精度一維/二維成像結果實現空間目標監視識別，獲取目標的尺寸、形狀、結構、運動等精細信息。一般情況下，要求對空間目標的觀測信號帶寬至少2 GHz以上，成像分辨力10 cm左右。因此，針對此類空間目標，尤其是空間碎片等小目標的精細結構通常小于距離分辨單元。而距離分辨單元與雷達的帶寬成反比，為進一步提高分辨率的一個簡單方法是升級雷達系統硬件以增加其帶寬。但是通過這種將單部雷達的帶寬設計的很寬從而提高分辨率的做法又面臨著雷達帶寬與威力性能、生產工藝水平、制作成本之間的矛盾。針對以上問題，一個更好的策略是求助于信號處理技術，比如說超分辨算法。通過對接收信號進行后處理來提高雷達分辨率，無需對原始雷達設備進行任何硬件修改。多頻帶帶寬相參合成技術，就是將超分辨算法應用于多個空間并置的不同頻帶上工作的雷達的數據相干融合技術。該技術對多段子帶回波進行相參合成，形成超寬帶觀測能力成為克服單雷達成像系統帶寬局限的一種有效方式。該方法與傳統方法相比，無需改變原始雷達體制和硬件設備，僅利用先進的信號處理技術就可實現雷達帶寬和成像分辨力的成倍增長。在保證原雷達探測威力的同時降低了超寬帶雷達研制難度和硬件成本，由此來看，多頻帶帶寬相參合成技術具有極大的現實研究意義和學術研究價值。

在1997林肯實驗室期刊發表了題為《Ultra-Wideband Coherent Processing》的論文[1]，成為最早開展多頻帶融合成像技術研究的實驗室。該論文公開了暗室實驗結果，展示出了多頻帶融合成像的巨大潛力，同時也拉開了多頻帶融合成像的大幕。在1999年，林肯實驗室的Cuomo第一次公開發表了基于兩部雷達回波數據的信息融合，成功的完成了真假彈頭的辨別實驗[2]，并首次闡述了多部雷達回波合成超寬帶的關鍵性技術。由于雷達觀測到的目標的回波在觀測的頻帶上具有緩變的特性，因此多頻帶雷達帶寬相參合成是可行的，可以用同一個回波模型來描述不同雷達的觀測回波。因此，也可以認為不同雷達的觀測回波是一個回波模型在不同頻帶上的觀測結果。相參合成就是在一定的數據約束下，借助多段已知觀測數據估計信號模型參數，再結合模型參數外推預測空缺頻段數據，最后將所有頻帶的數據融合，等效為一部超寬帶雷達的探測效果。在這個過程中，相參配準和帶寬外推融合成像是需要解決的兩個關鍵性技術。相參配準是將非相干的觀測回波進行相干化，使其滿足相參性，是該領域的難點和關鍵性技術之一；帶寬外推融合成像是將配準后的多段回波數據進行外推融合，使其成為一個大帶寬信號，從而得到探測目標更加精細的圖像。

2 相參配準研究現狀

1999年，Cuomo提出了一種用于不同頻帶上工作的多個空間并置雷達的數據相參融合技術。該技術首先將子帶進行互相關運算以補償不同雷達子帶之間的相移，然后用一個全極點模型擬合稀疏子帶的測量值，并用一種改進的求根多重信號分類(root-multiple signal classify,Root-MUSIC)算法估計其參數。最后，使用該模型對子帶之外的數據進行外推和插值[2]。類似的,文獻[3-4]對來自多波段空間分布的數據融合進行討論，其中不同的雷達具有不同的工作頻帶，并在不同的角度位置照射目標。

實際上，上述的超分辨率算法采用了衰減指數和(DE)模型,也稱為全極點模型或Prony模型[5-6]去擬合寬帶雷達數據并用現代譜估計技術估計模型參數，如求根-MUSIC方法[7]、矩陣束方法[8]、ESPRIT方法[9]等等。這種解決方案主要有以下幾個問題:

1) DE模型(全極點模型/Prony模型)并不能精確表示寬帶的幾何繞射行為，導致寬帶雷達數據與模型之間不匹配，限制了超分辨算法的精度。

2) 模型階數對算法性能有重要的影響，但Akaike信息量準則法(Akaike information criterion,AIC)和最小描述長度法(minimum description length,MDL)很難準確估計模型的階數。

3) 大多數譜估計技術通常對噪聲敏感，這抑制了它們在真實場景中的魯棒性。

針對以上問題，學者們主要從參數估計和全極點模型的選擇兩方面進行了研究與改進。

2.1 基于模型參數估計的改進

2008年，為解決傳統的基于改進的Root-MUSIC融合方法的極點不匹配問題，Ye F等[10]提出了一種基于頻譜估計和幅度相位誤差模型方法來補償雷達子帶之間的非相干，使用二維融合來改善分辨率，并開發了一種新的擴展矩陣增強矩陣束(extended matrix enhancement and matrix pencil，EMEMP)算法。同年，徐少坤等[11]將雷達的二維成像矩陣束算法引入到聯合的多雷達觀測融合成像上，并利用多雷達觀測到的數據估計散射中心參數，從而提高了雷達成像的分辨性能。2009年，針對改進的Root-MUSIC的傳統融合方法對噪聲較敏感且存在模型極點失配問題。葉釩等[12]通過將MEMP(matrix enhancement and matrix pencil)的二維頻率估計方法推廣到稀疏數據域,并提出一種基于擴展矩陣增強矩陣束(EMEMP)的融合新方法。該方法首先以滿足增強矩陣束算法的配對要求構造每一維聯合增強矩陣，接著利用MEMP算法估計模型的極點并對極點進行配對，估計模型系數。最后，利用內插頻譜融合成像。該方法在解決極點估計失配問題的同時，提高了模型參數的估計穩健性。2016年，鄒永強等[13]為了彌補經典Root-MUSIC融合方法抗噪性能差的問題，提出了一種基于矩陣束算法的多頻帶信號極點估計方法。為了處理子帶信號之間的互不相干，通過每個子帶對應極點的關系來求解非相參參數。然后，引入一種以最小化信號差2范數為目標的迭代算法來減小信號融合誤差。仿真數據表明了該方法在低信噪比下也能夠獲得較好的融合效果。2017年，B.Hussain等[14]提出了一種改進的自回歸(auto-regressive,AR)相干稀疏帶處理算法，針對前所未有的小分數帶寬(2.2%)分析其增強AR算法的性能。通過使用基于光子學的多波段雷達保證波段之間的相干性，跳過[2]中提出的相位配準過程將計算成本降低了40%，并且還提供了2個子帶極點的精確估計。另外，通過實現高斯-牛頓算法使得非線性回歸與各極點相位的精確估計相結合，從而快速收斂到最佳擬合模型參數。

2.2 基于模型選擇與參數估計兩方面的改進

2005年，賀治華等[15]將基于衰減指數和模型的多重信號分類算法替換為可以精確描述高頻電磁散射特性的幾何繞射模型，對多重信號分類算法進行改進，利用特征分析方法的信號與噪聲子空間正交特性,使改進后的MUSIC算法不僅能夠精確估計目標散射中心位置,而且能估計散射中心類型,取得了不錯的效果.2010年，Shao Ming等[16]提出了一種基于GTD模型的二維狀態空間方法，用來估計超寬帶條件下運動目標的散射中心參數，并最終取得了相對不錯的精度。2013年，占榮輝等[17]在幾何繞射理論模型下，分析雷達回波的稀疏特性，將參數估計問題轉化為壓縮感知理論中的稀疏信號重構問題,據此提出了一種基于壓縮感知的2維GTD模型參數估計方法。在支撐區域內對散射中心的GTD模型參數進行估計,最后利用聚類方法和最小二乘算法對估計結果進行修正。有效改善模型參數的估計性能,提高散射中心類型參數的估計精度。2014年，Tian Biao等[18]主要針對稀疏子帶融合成像給出了一種基于幾何繞射理論(GTD模型)的高精度參數估計方法。考慮到各子帶回波的不相干問題，采用了相干處理方法。定點模擬數據的實驗結果表明，基于該方法的一維距離像和二維逆合成孔徑雷達(ISAR)圖像的分辨率優于各子帶。

此外，Paul Berry等[19]利用稀疏重構技術，研究了通過相干合成窄帶雷達數據獲得非合作目標識別的高分辨一維距離像，提出了一種壓縮感知的多通道雷達帶寬拼接技術，探討了存在相位誤差情況下，使用修剪的正交匹配追蹤(pruned orthogonal matching pursuit,POMP)算法和L1范數正則化解算器來解決稀疏頻帶帶寬的拼接問題。仿真結果表明，相對于正交匹配追蹤(orthogonal matching pursuit,OMP)和傳統以及改進的L1范數正則化，POMP有著顯著的性能提升。

以上方法大部分都是基于全極點模型的極點進行相參化，但這需要在正確估計子帶全極點模型極點的基礎之上完成。然而，此類方法在實際處理中依然存在著很難精確估計模型階數，擴展目標散射點數目眾多，可能大于可估計的極點數目的問題[20]。針對以上問題，TianJihua等[21]提出了一種新的現代譜估計的方法，即利用全相位快速傅里葉變換(All-phase fast Fouriertransform)算法和迭代自適應方法進行多波段雷達信號融合。該方法通過全相位快速傅里葉變換算法對各子帶之間的不相干量進行補償，然后將迭代自適應應用于信號融合的互相關子帶測量中，從而有效的避免了極點估計問題，如圖1所示的相位差補償效果。

圖1 相位差補償效果曲線

除此之外，部分研究者受到Cuomo提出的將子帶之間的非相參相位分為線性相位和固定相位兩部分，對子帶信號建立全極點模型，通過估計各子帶極點的參數，并構建以非相參相位為變量的代價函數來求解線性相位項和固定相位項方法的啟示。研究發現，雷達一維距離像間的平移量可以反應出線性相位項的差異，進而利用此關系求解線性相位項，定義代價函數求解固定相位項[22-25]。這類方法相比于以上方法而言，減少了一定的計算量，簡化了算法。由于是先求取線性相位項并加以補償，因此固定相位項的求取并不受線性相位項的影響，精度相對較高。但也存在一些問題，例如固定相位項的求取受到線性相位項求取精度以及定義的相干函數及全局搜索步長的影響很大。

3 融合成像研究現狀

在相參配準(相干處理)之后，多個子帶之間相互相干，滿足了模型擬合的條件。對于多子帶融合，模型擬合極其重要，因為模型擬合的精度決定了合成信號全頻帶的精度。林肯實驗室的研究人員提出了一種超分辨率算法，使用所謂的全極點模型來擬合頻率數據。傳統研究工作者則在此基礎上進行了改進，主要是建立全頻帶全極點模型。通過相參配準后的子帶回波數據進行帶寬外推和插值，補全空缺頻段數據，從而得到融合后的全頻帶信號。

3.1 基于全頻帶全極點模型

2013年，田彪等[26]基于GTD模型提出了一種高精度參數估計算法，去解決多頻帶帶寬相參合成的相參配準問題。這種方法通過來自不同頻帶的全極點模型中，中心幅度以及極點的相位差來估計不同頻帶的非相參量。利用缺損數據幅度相位聯合估計方法對相參配準后的頻帶數據填補，最后再以補全后的全頻帶數據對幾何繞射-全極點模型的參數進行高精度估計，得到融合以后的全頻帶數據。2014年，Zhang Huanhuan等[27]采用了一種類似于文獻[1]的方法。首先用各個子帶的全極點去擬合數據，然后利用相干函數擬合后的兩個子帶全極點模型進行相參配準；接著用基于GTD模型的參數構建冗余字典，快速稀疏貝葉斯學習算法來計算字典原子權重，以最終的權重和字典原子來測量子帶并進行插值和外推。2019年，Xiong Di等[28]提出了一種用于多波段雷達信號融合ISAR成像的子波段互相關補償方法，該方法將線性相位項和固定相位項補償過程解耦。使用酉-旋轉不變技術估計參數(unitary estimation of signal parameters via the rotational invariance techniques，U-ESPRIT)方法提高每個子帶極點估計的精度，并僅使用與相同強散射體一一對應的每個子帶的有效主極點，進一步提高了線性非相干相位的估計精度。此外，通過對每個子帶信號應用基于相同旋轉中心的相位自動聚焦方法來補償子帶之間的固定相位項，從而有效地補償子帶之間回波的初始相位差(固定相位項)。

由于全頻帶全極點模型實現的線性預測方法容易受到回波數據信噪比的影響，而且采用這類方法重構的分辨率往往不高。近年來，現代譜估計和稀疏信號處理技術的引入給多頻帶融合提供了更多優化的解決途徑，有效的避免了傳統方法對估計模型階數精度的要求[21,26-27,29-32]。

3.2 基于稀疏子帶表示

2013年，Bai Xueru等[19]基于稀疏子帶表示，導出空間目標雷達成像的幾何繞射信號模型，并介紹分析了可用方法。提出一種適用于高速運動空間目標稀疏子帶成像方法，該方法包括距離和方位相位補償、間隙數據填充、散射體數目估計、幅度估計和方位圖像融合。最后，利用定點和電磁散射模型對模擬數據進行成像，從而證明此方法的有效性。2018年，Hu Pengjiang[33]針對逆合成孔徑雷達成像領域，越來越多的小目標表征需求，提出一種新的稀疏子帶成像框架。該方法首先對每個子帶進行精細成像，通過精細成像補償子帶回波數據之間的高階相位誤差。然后進行梯形變換以統一子帶的圖像尺度，并對稀疏子帶進行相干處理，執行跨距離壓縮增強返回的稀疏性，以此獲得可觀的信噪比增益。最后，基于自回歸模型對跨距離單元的壓縮子帶回波數據進行插值，通過平滑l0算法重建高分辨率距離像(HRRP)。該方法提出的框架不需要填充子帶之間的空隙，并且對于帶隙具有魯棒性。

近年來的研究從原理和實踐上證明，稀疏貝葉斯學習[31-32](sparse bayesian learning，SBL)等貝葉斯方法可以獲得更好的稀疏恢復性能，廣泛應用于波達角方向估計[34]和雷達成像[35]。在多頻帶融合成像應用中，與現有的參數譜估計方法(如Root-MUSIC和凸稀疏近似算法[27])相比，尤其是在惡劣的受限等距特性(restricted isometry property,RIP)條件下,SBL方法表現出優越的性能。

2017年，Ma Juntao等[30]針對稀疏孔徑的多頻段高分辨力成像，提出了一種基于波形融合字典的新方法，并進一步討論了如何構造一維和二維融合字典，引入拉普拉斯先驗的貝葉斯方法求解欠定方程。利用融合字典與多頻段信號的匹配結構，避免了傳統的基于快速傅里葉變換或者經典譜估計方法所帶來的多頻段融合的非均勻和帶隙譜問題。因此，該方法不需要采樣、插值或外推操作從而避免了更多誤差的引入。2018年，Zhou Feng等[32]提出了一種基于貝葉斯學習的高分辨率稀疏子帶成像方法，構建了概率模型并借助稀疏貝葉斯學習算法進行最終的融合成像。

4 技術難點

4.1 相參配準

相參配準是對非相干相位估計與補償的過程，而非相干相位主要是指線性相位項和固定相位項。針對線性相位的差異估計方法較多，精度也較高；但是對于固定相位項的估計精度較低。然而，相參配準的難點就是對于非相參量的估計與精確補償。具體的估計方法可以大致分為兩大類：

1) 將多部不同頻帶雷達中的某部雷達的回波作為參考回波，其余回波乘以非相干量，共同構建一個雷達回波之間滿足相干性的相干函數；并利用優化算法搜尋，求取非相干參量。此類方法的參數估計精度高，但僅適用于高信噪比條件，計算量大且容易陷入局部極小值。

2) 基于全極點模型的極點進行參數化，即利用線性相位差異在極點中而固定相位差異在幅度系數中的結論，結合MUSIC、ESPRIT、矩陣束法等參數估計方法直接估計子帶模型參數，進而反推出線性相位項和固定相位項的值。這類估計方法需要在正確估計子帶全極點模型極點的基礎之上完成，而在實際處理中受噪聲等因素影響很難精確估計模型階數。此外，這類方法不適用于散射體眾多的復雜目標。

現階段，針對以上問題。文獻[21]提出全相位快速傅里葉變換算法和迭代自適應方法進行多頻帶雷達信號融合。文獻[37]提出了一種基于有效極點和相位自動聚焦的相干處理方法用于補償多頻帶雷達信號融合成像中子帶間的非相干相位。通過子帶極點相位序列的最大互相關提取有效極點，然后重新排序,估計線性非相干相位；對于固定相位的估計，將各子帶回波分別采用能有效補償隨機初始相位的相位自動聚焦算法，從而有效的消除了噪聲對非相干相位估計的影響。仿真的結果驗證了該方法的有效性和噪聲不敏感性。如圖2所示[37]，線性相位項估計誤差隨噪聲的變化情況,其中A1為傳統方法[36]。

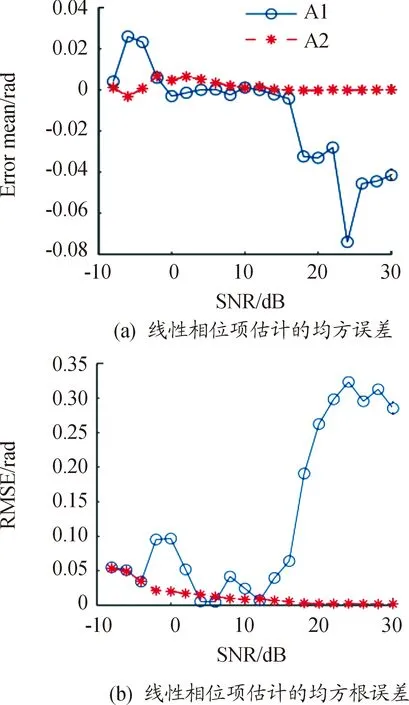
圖2 線性相位項估計誤差的均值和均方根隨噪聲的變化曲線Fig.2 Variation of the mean and root mean square of the estimation error of the linear phase term with noise

4.2 融合成像

稀疏子帶外推融合成像的最新技術主要包括：現代譜分析、稀疏信號表示以及稀疏貝葉斯學習。

1) 現代譜分析。現代譜分析的典型方法主要是間隔數據幅度和相位估計(gapped data amplitude and phase estimation,APES)為了實現精確的譜估計，可迭代優化幾次直到收斂。此方法與傳統的基于全頻帶全極點的參數譜分析技術相比，對模型失配和噪聲具有更強的魯棒性。但是，該方法在低信噪比下可能會引起較大的估計誤差。

2) 稀疏信號表示。稀疏信號表示是將稀疏子帶成像問題轉化為稀疏信號重構問題。利用雷達觀測目標散射中心的稀疏性，通過構建完備字典、求解線性方程等操作估計目標散射中心信息，進而重構信號的全局模型。該方法作為高概率重構信號方法存在失效的可能且迭代次數較多，計算量較大。

3) 稀疏貝葉斯學習。稀疏貝葉斯學習是通過構建適當的統計圖形模型，在x軸上施加稀疏性促進先驗，然后在貝葉斯框架中估計模型參數。例如文獻[27]將高斯分布引入到x軸和噪聲中并應用快速相關向量機[38-41]自適應地選擇與數據相關的字典原子計算它們相應的權重。由于快速相關向量機算法具有從模型中刪除基函數的操作，因此減少了矩陣求逆的計算負擔。另一方面，算法的最佳收斂閾值隨信噪比和散射中心的位置而變換，選擇不當可能導致性能不佳，如幅度估計不足和散射中心重建不正確。

5 結論

從多頻帶融合成像研究的幾十年發展歷程來看，利用稀疏子帶進行數據合成的高分辨率成像技術受到了廣泛的關注。其中，稀疏貝葉斯學習等貝葉斯方法具有更好的稀疏恢復性能，逐漸應用于稀疏子帶回波表示的多頻帶融合成像中。

但是，不論基于全頻帶全極點模型、譜估計方法還是稀疏信號處理技術的多頻帶融合成像處理方法，都更多的停留在利用仿真數據、單部雷達數據切分、微波暗室數據等手段驗證融合成像方法的有效性。直到目前為止，還沒有真正的多頻帶合成實地測量數據處理結果的報道。但是，實際的多頻帶帶寬融合成像所遇到的問題較多，理論模型很難完全適用于實際情況且多部雷達的相干性要求更高等。因此，目前的理論研究成果并不能很好的應用到實際情況中。在接下來的研究中，應該更加注重復雜電磁環境下，多頻帶帶寬合成技術目標仿真與驗證以及實測數據的采集與應用，進而更好的指導實踐。本文，對多頻帶帶寬相參合成關鍵技術進行研究，并對其中最為關鍵的相參配準和帶寬外推融合成像技術的技術難點與現狀進行分類綜述。