高階思維訓練的課程內容設計
——以材料力學典型例題為例

李 敏 李芷菡 陳偉民,

?(北京航空航天大學航空科學與工程學院,北京100191)

?(中國農業大學食品科學與營養工程學院，北京100193)

??(中國科學院力學研究所，北京100190)

為了提高教學質量，近年來在教育部持續推動下，一流課程(金課)建設成為全國高校教育教學改革的重點工作。作為一流課程的主要特征，“兩性一度”(高階性、創新性與挑戰度)已經廣泛出現在各級各類教學要求與制度中，其核心在于利用“創新性”的方法，通過具有“挑戰度”的訓練，達到培養“高階性”思維的目的。

相比以記憶、理解與應用為特征的低階思維模式，高階思維模式(分析/評價/創造)體現在對問題的認知經歷“盲目相信/眾說紛紜/批判思維”的過程，最終建立基于自身理解的、對客觀事物全面與深刻的認識。達成該目標的關鍵在于教學內容的設計--通過具有挑戰性問題的教學內容與環節，引導學生全面思考與深入探究，逐步形成批判性思維模式。

對于理工科專業課程，盡管不同課程在性質與內容上不盡相同，但總體而言，通過以下方面引入問題與思考是有益的：

(1)相關內容的內在關聯；

(2)假設條件的適用范圍；

(3)問題的物理/數學本質。

為了不偏離課程主體內容，并且考慮到受眾比例，挑戰性問題的課程內容設計需要滿足：起點低、臺階小、空間大，在這一點上，非常類似于各類電子游戲的設計。為了說明以上思路，本文以材料力學課程教學的一個實例展示問題引導與啟發過程。

1 原始問題與標準解答

課程內容設計的出發點最好基于教科書的題目與敘述，這就是所謂的起點足夠“低”。

在材料力學或彈性力學有關功(位移)的互等定理部分有如下或類似的習題[1-2]：

圖1所示等截面直桿，承受一對方向相反、大小均為F的橫向集中力作用。設截面橫向尺寸為b、拉壓剛度為EA，材料的泊松比為μ。試利用功的互等定理，證明桿的軸向變形為?l=μbF/(EA)。

圖1 第一種受力狀態示意圖

該題目簡單而典型，也常常被教師選擇作為例題講解，教科書給出的標準解答如下。

對于該桿件構造另一種載荷狀態如圖2所示，在桿件上施加一對大小相等，方向相反的軸向力F1。

圖2 第二種受力狀態示意圖

在F1作用下，桿的橫向變形為

根據功的互等定理，對于兩種受力狀態有

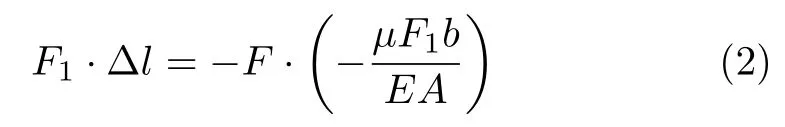
由此得

2 提出疑惑與概念辨析

除了教科書給出的標準解答，這里展示另一種模式的證明。首先，為了方便后續講解與符號說明，把圖1中結構畫為三維模式，見圖3，載荷F作用面的橫向尺寸為h，軸向長度為l。

圖3 結構三維尺寸與圖標

在F作用下橫向應變為

軸向應變

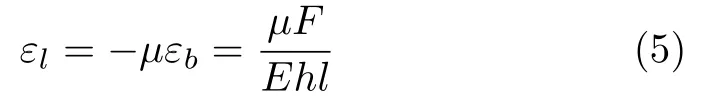
軸向變形

比較式(3)與式(6)可以發現，答案完全一致。

該證明模式并不完全由教師“制造”，由于此例為教科書上作業題，筆者多年統計數據，發現有25%以上的學生給出了第二種模式的證明過程。

事實上，引發學生思考的出發點從學生作業錯誤或者學生日常問題入手是最為合適的，因為其符合學生思考問題的思維模式。

該證明的錯誤之處在于：面ABCD上橫向載荷F為集中力，在長度l范圍內無論橫向應力或應變都是非均勻分布，式(4)所得橫向應變表達式在全局范圍內不正確。

該證明“找錯”的過程，對于辨析概念與對象，例如應力與平均應力，集中力與分布力，微元體與分離體等方面，教師引導學生進行問題討論是有益的。

3 擴展研究與理解進階

盡管上面給出的證明模式是錯誤的，但是根據式(4)～式(6)給出的最終結果與正確答案卻完全一致，由此可以提出的下一個問題是：答案一致是一種“巧合”還是有其“必然”？

這個問題可以隨著上面討論與講解一次性提出，但是學生立刻就能給出比較全面的解答是不現實的，可以作為思考題布置并在下一次作為專題研討。為了在學生討論時引導重點與主線，教師完成相關課程內容設計作為預案是有益的，以下問題的分析展示了逐步提升思維訓練的過程。

3.1 載荷從均勻分布到集中作用

首先，盡管式(4)～式(6)的證明過程對于原題是錯誤的，但對于作用于ABCD與A′B′C′D′的橫向均布面載F/(hl)而言(見圖4(a)，為了文本簡潔，受力圖均為正視圖，下同)，該證明過程是正確的。

圖4 載荷分布范圍變化示意圖

其次，當均布載荷在軸向的作用范圍僅為ABCD的一個局部，例如l1(l1

最終，上述模式的極端情況，當l1→dl(圖4(c))，

以上的證明過程是基于均勻應變以及極限化模式，同樣可以采用構造如圖2的軸向載荷狀態，利用功的互等定理得到同樣結果，此處不再贅述。

從該變化過程可以看出，無論載荷分布形式與位置如何，對于靜力等效的一對橫向作用力，其在軸向引入的變形均為同一數值，所以第二節中盡管證明過程是錯誤的，但是答案完全一致有其必然性。

事實上，我們可以把以上的證明與分析結果畫在一張圖上(如圖5)：隨著載荷集度的增加，在載荷作用范圍內，軸向變形的集度也線性增加，但總變形(對應于虛線包圍的面積)保持不變，極限狀態為載荷分布范圍趨于零，此時變形集度趨于無窮大，但二者乘積(總變形量)為一有限值并保持不變。

圖5 軸向變形集度(應變)分布與變化

以上分析過程中有多個“臺階”，每次上升的幅度不大，而且相互關系緊密，最后的總結已經在數學本質上有所體現。

3.2 載荷分布從局部平衡到總體平衡

觀察圖4中各種載荷分布狀態，盡管軸向分布區域不同，但橫向均為對稱模式，即任意局部尺度上載荷都是平衡的；如果載荷只是總體平衡而非各局部均平衡，如圖6所示各種狀況，軸向總變形會發生變化嗎？

圖6 載荷分布平衡方式示意圖

解決這類載荷分布狀況比較簡單的方式是采用疊加方法：

(1)當上下表面載荷互換時，所產生的軸向變形完全相同，所以這兩種載荷疊加后獲得的軸向變形為單獨載荷狀況的2倍；

(2)疊加后的載荷可以重新分解為與圖4類似的橫向對稱模式的組合，可以采用上節中的計算方法得到完全一致的結果。

可能這種處理方式不是唯一的，但以此為基礎引導學生討論是有趣的。

相比上節限定于原始問題，學生主動想到這類載荷分布狀況的可能性較小，但對該問題處理的方式體現了利用已有知識與方法解決新問題的靈活性。

3.3 載荷分布方式引入的位移量級對比

與3.1節不同，在3.2節中載荷分布模式不僅導致軸向變形，而且伴隨著橫向彎曲變形，其一種分布模式的極端化狀態如圖7(a)，相當于懸臂梁自由端承受集中載荷如圖7(b)(受力簡圖)。對于該受力狀態導致的軸線變形?l仍然可以使用3.2節的計算方法，但是需要注意，由于彎曲變形的影響，軸線由直線變為曲線，在水平x方向(原始軸線方向)自由端也有水平方向位移?A。

圖7 不同方向位移比較示意圖

水平方向位移?A(如圖7(c))也稱為曲率縮短，通過撓曲軸總長與其水平軸投影之差進行計算[3]，通用計算公式是泰勒展開的近似表達

材料力學中梁彎曲變形的分析基于純彎曲率公式，忽略了剪切影響并在小變形條件下進一步簡化獲得撓曲軸方程。經典教材中均提及忽略梁軸線方向的位移[1,4-6](橫力彎曲條件下包括曲率縮短與軸線變形)，但一般都沒有給出各量量級的討論，此處比較圖7中梁的自由端撓度wA，自由端水平位移?A，以及梁軸線長度變化?l的量級，對于理解基本概念是有益的(為了符合梁彎曲的圖注習慣，下列公式中載荷作用方向的截面橫向尺寸改為h)

在小變形條件下，各變形(位移)量相對于梁長度均為小量，撓度wA是學生們非常熟悉的量，根據式(10b)與式(10c)中與wA的比較，水平位移?A與軸線長度變化?l均為撓度wA的小量，相對而言

使用彎曲應變εM代入式(11a)

以常見彎曲應變范圍εM=1.0?4～1.0?3代入式(11b)評估比值，對于工程長梁，一般情況下?A至少比?l大一個量級。

梁的橫向位移有非常明顯的長度放大效應，與撓度wA和水平位移?A不同，軸線長度變化?l與梁的長度無關，這是其相對較小的主要原因。

該部分的討論關聯了課程內容中的不同章節，而且需要資料查閱與相關數學推導，體現了思維訓練的深度與廣度，展示了課程內容設計的“空間大”。

4 小結

知識結構與能力培養是專業培養目標的核心表述，課程教學的目的最終體現在支持學生學習并達成能力培養。在高階性思維能力的訓練環節中，教師主導的課程內容設計是難點：

(1)問題的引入不能完全脫離教材內容，須適合大部分學生水平，從教材內容、例題與習題出發是最佳途徑；

(2)能夠通過簡單分析運算獲得明確結論的問題比較好，工程實際問題影響參數較多且分析過程過于復雜更適合課程背景介紹，不宜作為課堂教學深入研討的內容；

(3)問題的討論可以在不同層次展開并關聯教材多個章節，便于學生進行概念辨析和知識體系構筑。

為了說明主體思路，本文從一個學生作業與問題出發，展示了批判性思維訓練引導過程，希望對于相關課程內容設計有一定參考價值。