基于非線性級聯系統的彈性關節空間機器人新型滑模控制1)

梁 捷 秦開宇 陳 力

?(電子科技大學航空航天學院，成都611731)

?(中國空氣動力研究與發展中心，四川綿陽621000)

??(福州大學機械工程及自動化學院，福州350116)

空間機器人系統能在航天器在軌服務技術中發揮重要作用[1-9]。在以往的研究中，許多學者關注了空間機器人系統中機械臂臂桿的柔性控制問題[10-13]。但需引起注意的是，彈性關節控制被認為比臂桿柔性控制更具挑戰性[14-15]。由于空間機器人關節系統設計中使用了大量諧波減速器等柔性元件，因此在空間機器人控制系統設計中若不考慮關節彈性振動，將會對控制精度及穩定性造成很大影響[14-16]。

當前，彈性關節空間機器人的控制算法主要分為奇異攝動法[14,17]和基于柔性補償的奇異攝動法兩類[18]。劉福才等[17]基于奇異攝動法，將柔性關節空間機器人分解為快、慢變子系統，并分別設計控制器，但該方法僅適用于彈性關節剛度較大的情況；陳志勇等[18]建立了基于柔性補償的奇異攝動修正模型并設計控制器，雖然可以應用于剛度較小柔性關節空間機器人的控制中，但隨著關節柔性剛度的進一步減小，控制效果并不理想。再者，由于奇異攝動分解理論的束縛，以上兩類控制算法很難運用于位置不控、姿態受控的空間機器人動力學模型。

近年來，滑模控制在空天領域得到廣泛應用[19-21]。戴巧蓮等[22]提出了一種基于干擾觀測器的空間機器人反步控制算法，但其觀測器設計的不足是：需測量角加速度，同時要求質量陣中主對角線上的項必須為常數；米根鎖等[23]設計了一種基于干擾觀測器的機械臂非線性滑模控制策略，其在干擾觀測器設計時假設干擾的變化是緩慢的，但這在實際應用中很難做到。

鑒于以上研究現狀，為實現彈性關節空間機器人在關節柔性剛度較小情況下的軌跡跟蹤及彈性振動控制問題，本文擬基于非線性級聯系統的概念建立雙臂彈性關節空間機器人系統動力學方程，并在此基礎上設計一種基于放寬條件改進型非線性干擾觀測器(nonlinear disturbance observer,NDO)的新型自適應動態終端滑模控制算法及力矩反饋控制算法。該算法可用于關節柔性剛度較小情況下空間機器人軌跡跟蹤及抑制彈性關節振動。

1 級聯動力學建模

目前，對空間機器人準確執行自主操作任務的要求不斷提高，這導致了對輕量化材料和機構的需求增加。因此，關節柔度效應變得非常重要，是實現空間機器人良好軌跡跟蹤性能的主要限制因素。文中應用圖1所示的雙臂彈性關節空間機器人系統開展改進型NDO、新型自適應動態終端滑模控制系統及關節彈性振動控制系統設計，圖1所示雙臂彈性關節空間機器人系統由載體B0，左、右臂B1，B2，B3，B4及柔性關節O1，O2，O3，O4組成。建立慣性坐標系xOy及分體Bi(i=1,2,3,4)的連動坐標系xiOiyi；此外，圖中θ0為系統載體姿態實際轉角，θim(i=1,2,3,4)為各關節驅動電機轉子轉角變量，θi(i=1,2,3,4)為各操作臂Bi(i=1,2,3,4)剛性連桿轉角變量，P2和P4為負載。

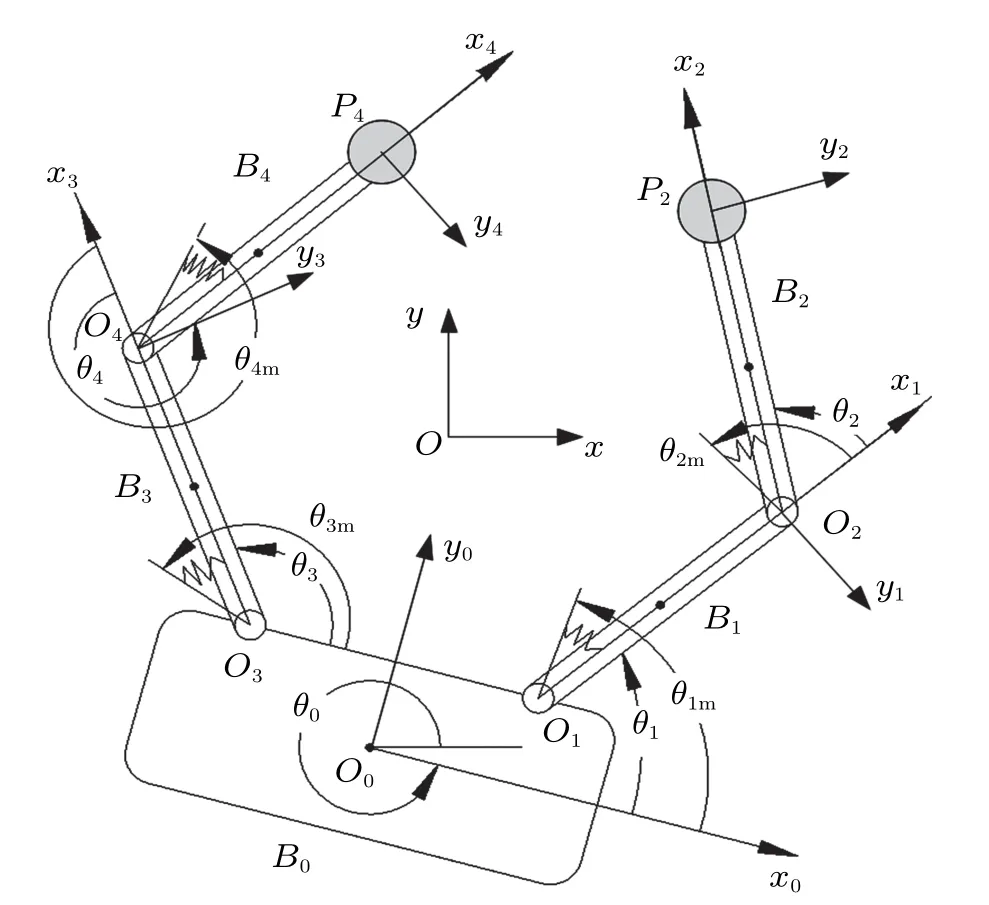
圖1 雙臂彈性關節空間機器人

1.1 彈性關節簡化模型

空間機器人彈性關節一般采用諧波減速器裝置，這些齒輪機構因其具有高減速比、體積小、重量輕、同軸裝配等優點而在空間機器人應用中受到越來越多的關注。然而，對于諧波減速器裝置，柔輪的彈性振動是控制系統開發面臨的重大挑戰。文中將彈性關節假設為一個線性扭轉彈簧[24](如圖2所示)，θm和τm為電機轉角和電機力矩。

圖2 柔性關節示意圖

1.2 動力學建模

考慮雙臂彈性關節空間機器人系統，假設每個關節被建模為恒定剛度的線性扭轉彈簧[24]，其非線性動力學模型是由拉格朗日公式在系統中存儲的動能和勢能導出的，具體建模過程如下。

由系統總質心定義及位置幾何關系，可導出

其中，ri(i=0,1,3)為Bi的質心OCi(i=0,1,3)相對慣性坐標系原點O的矢徑，r2為載體B2與載荷P2所組成的聯合體的質心OC2相對慣性坐標系原點O的矢徑，r4為載體B4與載荷P4所組成的聯合體的質心OC2相對慣性坐標系原點O的矢徑，Lij(i=0,1,2,3,4；j=0,1,2,3,4)均為系統慣性參數的組合函數，ej為xj軸的基矢量。

取系統廣義坐標矢量Q=[θ0,θ1,θ2,θ3,θ4,θ1m,θ2m,θ3m,θ4m]T。系統總動能為系統動能Tr和電機轉子動能Tθ之和。因此，有

式中，Tr=T0+T1+T2+T3+T4；Tθ=Tθ1+Tθ2+Tθ3+Tθ4；載體B0、機械臂B1和機械臂B3的動能分別為機械臂B2與載荷P2所組成的聯合體動能為機械臂B4與載荷P4所組成的聯合體動能為關節Oi處電機轉子的動能其中，分別為載體B0、機械臂B1和機械臂B3的質量；J0，J1，J3分別為載體B0、機械臂B1和機械臂B3的轉動慣量；m2P2和J2P2分別為機械臂B2與載荷P2所組成聯合體的質量和轉動慣量；m2P4和J2P4分別為機械臂B4與載荷P4所組成聯合體的質量和轉動慣量；ω0，ω1，ω3分別為載體B0、機械臂B1和機械臂B3的角速度；ω2，ω4分別為機械臂B2與載荷P2所組成聯合體和機械臂B4與載荷P4所組成聯合體的角速度；Jθi(i=1,2,3,4)為電機轉子的轉動慣量；z為中間變量。

在太空微重力條件下，系統的總勢能U表達為

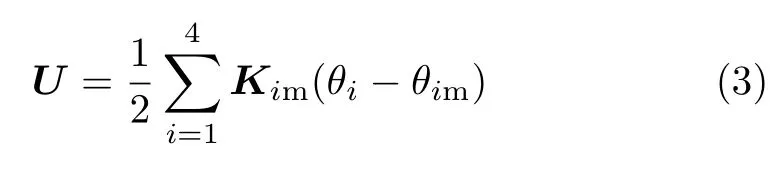
式中，Kim(i=1,2,3,4)表示第i個彈性關節的扭轉剛度。不失一般性，假設系統的初始動量、動量矩為零，即˙rC=0，于是系統動量、動量矩守恒關系可表示為

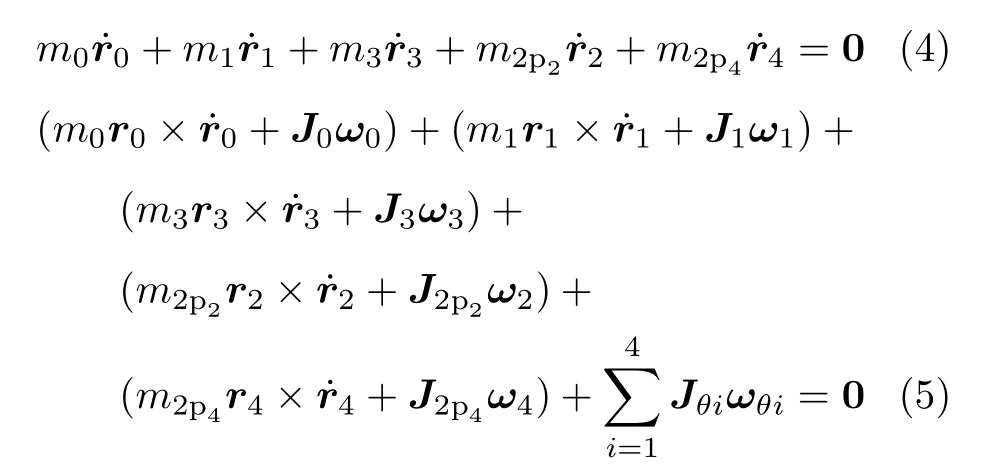
利用式(1)～式(5)、拉格朗日法及Spong假設，可導出雙臂彈性關節空間機器人級聯動力學方程

其中，式(6)為機械臂動力學模型，式(7)為關節動力學模型，兩模型式之間通過機械臂端輸入力矩τ而連接；M(q)∈R5×5為質量陣；R5×1為離心力、科氏力矢量，且對于任選列向量Z∈R5均滿足：θ2θ3θ4]T為載體姿態角與關節角組成的向量。θm=[θ1mθ2mθ3mθ4m]T和Jm=diag(J1mJ2mJ3mJ4m)分別為關節電機的轉角列向量和對稱正定轉動慣量陣；Km=diag(K1mK2mK3mK4m)為扭轉剛度陣，Kim(i=1,2,3,4)表示第i個彈性關節的扭轉剛度；τ0為載體姿態角控制力矩；τm∈R4為關節電機實際輸出力矩列向量。轉角誤差δ=θm?θ。

為更好設計雙臂彈性關節空間機器人控制器，建立了式(6)～式(8)組成的空間機器人級聯動力學方程，因為級聯系統在限定范圍內具有全局漸近穩定性，因此，更加適用于彈性關節空間機器人控制器設計[25-26]。

2 控制算法設計

本研究提出的控制策略采用基于非線性級聯系統的方法。該方法應用于柔性關節空間機器人，為設計控制算法提供了一種思路。該控制算法的基本思想是：首先，將整個空間機器人系統視為由機械臂動力學模型、關節動力學模型及兩模型式之間通過機械臂端輸入力矩τ而連接組成的級聯系統；其次，為這兩個動力學模型分別設計具有級聯關系的內、外環控制器；再次，將關節輸出電機轉子轉角θm視為機械臂動力學模型的控制變量，設計虛擬的電機轉角θfm以實現關節軌跡跟蹤控制；而后，針對關節彈性易產生振動的實際工況，設計τm，使電機輸出轉角θm跟蹤虛擬控制量θmf，即使機械臂端的實際輸入力矩τ=Kmθm快速跟蹤機械臂的虛擬輸入力矩?τ=Kmθmf(其中?τ=τ??τ代表了關節彈性振動)，從而抑制關節彈性振動。文中級聯控制原理如圖3所示，qd為載體姿態及關節角的期望軌跡。

圖3 級聯控制原理圖

2.1 機械臂動力學模型控制算法設計

文中機械臂動力學模型式(6)采用基于放寬條件改進型NDO的新型自適應動態終端滑模控制算法，其算法設計思路是：為有效消除參數不確定和未知干擾對空間機器人控制性能的影響，首先設計放寬條件的改進型NDO對系統集中不確定項D進行估計，并證明觀測誤差的收斂性，然后，再對其與實際估計用新型自適應終端動態滑模控制來補償，系統控制框圖如圖4所示，d為外部擾動力矩。

圖4 機械臂動力學模型控制框圖

為便于算法設計，將機械臂動力學模型式(6)寫為

2.1.1 放寬條件的改進型NDO設計及穩定性分析

定義NDO觀測誤差為

由式(9)和式(10)可得觀測器動態方程

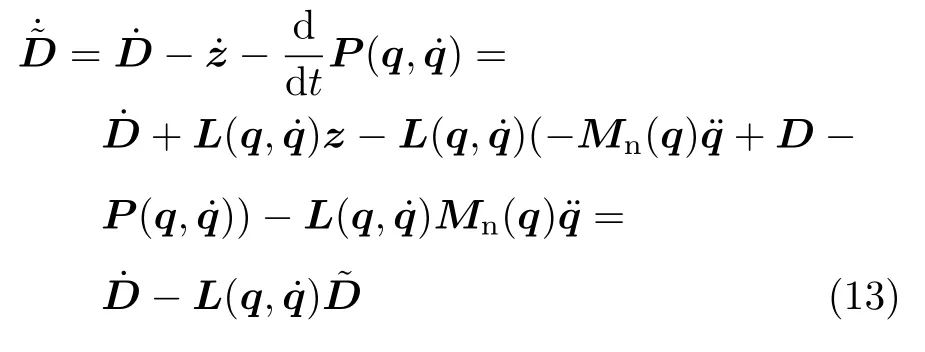
觀測器增益函數選取為

其中，X為可逆的正定常數矩陣，由式(11)得

定理1：針對機械臂動力學模型式(9)，設計改進型NDO式(10)，其觀測器增益函數選取如式(14)，輔助矢量函數為式(15)。在下列假設成立的情況下，觀測誤差能以指數收斂率收斂于相應區間。若擾動為緩慢信號，即˙D≈0，則觀測誤差將收斂于零。

假設1：存在一個對稱正定矩陣Γ，滿足不等式

假設2：集中不確定項的變化率有界，即?k>

有觀測器觀測誤差全局一致最終有界，并以(1?ξ)λmin(Γ)/(2σ2)‖X‖2收斂，收斂區間半徑為2kσ2‖X‖2/[ξλmin(Γ)](0<ξ<1)。

證明：構建改進型NDO的正定Lyapunov函數

式(17)對時間求導，得

因此，得

考慮正定Lyapunov函數式(17)、式(16)和式(19)，可得

利用Rayleigh-Ritz不等式[27]

可得

即

由式(25)，得

結合Rayleigh-Ritz不等式(22)及式(21)，得

由于Γ是對稱正定矩陣，因此

由式(26)～式(28)，可得

其解析解為

由式(17)及Rayleigh-Ritz不等式(22)，得

再結合式(30)和式(31)，可得

可見，觀測誤差能以指數收斂率收斂于λmin(Γ)/(2σ2‖X‖2)相應區間。若擾動為緩慢信號，即≈0，則觀測誤差將收斂于零。

證畢。

然而，基于擾動為緩慢信號的假設是很難滿足工程實際需要的，這限制了NDO的應用，因此，針對該情況，放寬對擾動信號變化率的限制，在新的條件下設計改進型NDO。

假設系統擾動變化率放寬為

式中，σ為未知正常數，則觀測誤差動態方程為

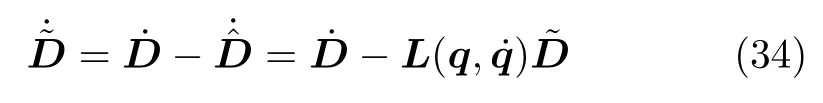
求解式(34)，得

因此，觀測器誤差可收斂到球域內

式中，r(Bd)為球域半徑，通過設計可使得r(Bd)足夠小。

2.1.2 新型自適應動態終端滑模控制算法設計

由于空間機器人系統存在系統動量守恒約束關系，所以上節設計的放寬條件改進型NDO也很難精確估計系統集中不確定項D，假定補償后仍存在觀測誤差且滿足不等式基于此，本節設計新型自適應終端動態滑模控制算法對觀測誤差進行有效補償。該算法顯著優點為：通過采用自適應動態滑模切換項，克服了慣常滑模趨近律需要預知不確定上界的缺點，因為對于復雜系統，不確定上界是很難預知的；同時，降低高頻抖振提高了控制精度。

該控制算法由等效控制項和切換控制項兩部分組成，具體設計步驟如下。

首先，設計滑模面

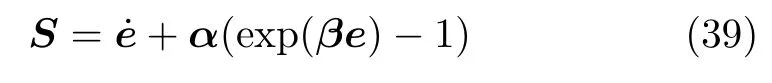
式中，e=qd?q為跟蹤誤差；α,β∈R5×5為對角正常數矩陣。

再次，設計自適應動態滑模切換項

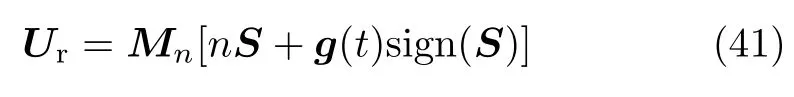
式中，n為正常數，g(t)為待設計的參數。

將等效控制項式(40)、動態滑模切換項式(41)及放寬條件改進型NDO的補償項?D結合起來，則機械臂動力學模型式(9)的控制律為

定理2：針對式(9)描述的雙臂彈性關節空間機器人機械臂動力學模型，如果滑模面設計為式(39)，結合放寬條件的改進型NDO式(10)，采用新型自適應動態終端滑模控制算法為式(42)，選取參數和的自適應律分別為

式中，ρi(i=0,1,2)為學習率，則系統漸近穩定收斂。

證明：取Lyapunov函數

為保證系統狀態能夠運動到滑模面上，控制算法應滿足滑動模態條件，即當設計

式中，λ為正常數矩陣。

將式(43)、式(45)和式(46)代入式(44)可得

式中，n和ε為正常數。因此，被控系統漸近穩定收斂。其中，推導過程使用的范數默認為2-范數的平方。在工程實踐中，要進一步降低滑模控制中存在的高頻顫振以提高控制精度，在式(42)中，利用函數tanh(·)代替符號函數sign(·)，則機械臂動力學模型式(9)的控制律式(42)改進為

2.2 關節動力學模型控制算法設計

空間機器人關節的彈性振動給機器人的控制帶來了很大的挑戰，如果在控制系統設計中忽略了關節柔度的影響，會導致系統不穩定甚至失控。基于此，文中設計基于力矩反饋的內環控制律τm來抑制關節諧波減速器裝置引起的彈性振動。?τ=τ??τ代表彈性關節的彈性振動特性。即，設計關節電機驅動力矩τm，使τ快速跟蹤?τ。

設計基于力矩反饋的關節動力學模型控制律

其中，k2,k3均為設計參數。將式(49)代入式(7)，可得

由式(50)可得

由于，k2/k3>0，因此關節動力學模型的閉環控制系統有界輸入、有界輸出穩定性。

綜上所述，雙臂彈性關節空間機器人的控制系統由式(7)～式(9)、式(48)和式(49)組成，控制律式(48)和式(49)存在級聯關系。相較于奇異攝動控制方案，基于級聯法的控制算法的顯著優點是：控制方案理論上不受關節剛度大小的約束，同時，能夠運用于文中位置不控，姿態受控這種電機轉子數與關節數不對等的彈性關節空間機器人數學模型。

3 仿真研究

為了校驗本文提出的改進型NDO設計、新型自適應動態終端滑模控制和彈性振動抑制控制算法的有效性，對圖1所示的雙臂彈性關節空間機器人系統進行數值仿真，仿真選取的模型參數：載體B0的質量和轉動慣量分別為m0=40 kg，I0=34.17 kg·m2；兩臂首桿的質量和轉動慣量分別為m1=m3=40 kg，I1=I3=1.5 kg·m2；兩臂末桿的質量和轉動慣量分別為m2=m4=1 kg，I1=I3=0.75 kg·m2；設柔性關節Oi(i=1,2,3,4)的扭轉剛度為Ki=15 N·m/rad(i=1,2,3,4)，關節電機轉子轉動慣量為Ji=0.8 kg·m2(i=1,2,3,4)；O0沿x0，y0方向距O1(O3)長度為Lx=2 m，Ly=1 m；左、右臂B1，B2，B3，B4的桿長為Li=2 m(i=1,2,3,4)。

設系統仿真時間t=10 s，利用控制律式(48)和式(49)對圖1所示空間機器人系統進行數值仿真，各臂桿關節運動軌跡為θ0d=sin(πt/4)/3，θ1d=cos(tπ/3)+π/3?1，θ2d=sin(tπ/3)+π/3，θ3d=cos(tπ/3)+2π/3?1，θ4d=sin(tπ/3)?π/3.θ0d，θ1d，θ2d，θ3d和θ4d的單位為rad，且系統初始構型為θ(0)=[0.2,0.8,1.2,1.8,?0.8]Trad，θm(0)=[0.8,1.2,1.8,?0.8]Trad。

控制參數選擇為α=β=diag(5,5,5,5,5)；X?1=diag(120,120,80,120,80)；k2=20；k3=1；n=ε=4。

用于比較的控制方案中參數k4=k3；k5=k2；k6=k3。

參數自適應律的初始值為ηi=0。

為驗證文中設計級聯控制算法的有效性，仿真將對以下兩種算例進行討論比較，仿真結果如圖5～圖10所示。

圖10 右臂關節角θ3,θ4的三種控制算法軌跡跟蹤圖(關節柔性剛度15 N·m/rad)

3.1 算例1：開啟/關閉改進型NDO及自適應律

圖5～圖7分別給出了文中設計控制算法在開啟和關閉系統中觀測器補償項?D及式(29)中參數，和自適應律情況下，載體姿態角關節角θ0的對比情況，左臂關節角θ1和θ2的對比情況，右臂關節角θ3和θ4的對比情況，可以看出，若沒有對文中自適應終端動態滑模控制算法進行觀測器估計及動態滑模參數自適應律設計，僅通過動態終端滑模控制會大大降低空間機器人的控制精度。

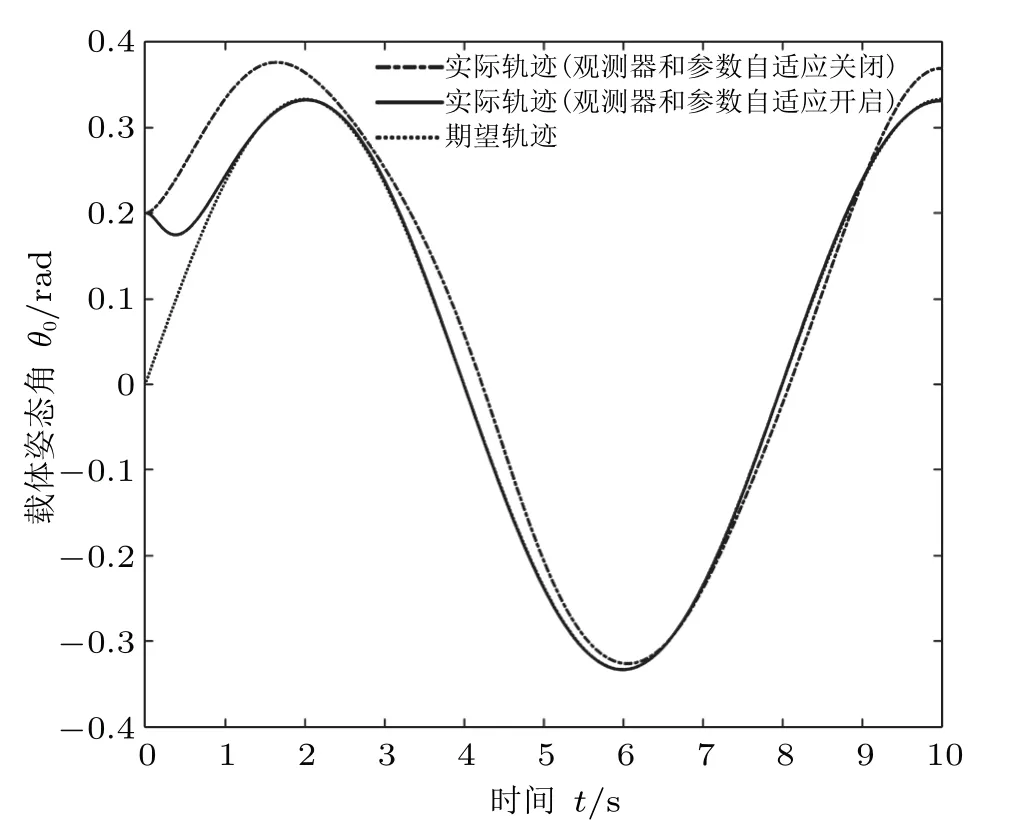
圖5 載體姿態角θ0軌跡跟蹤圖(觀測器和參數自適應律開啟與關閉)

圖6 關節角θ1和θ2軌跡跟蹤圖(觀測器及參數自適應律開啟與關閉)

圖7 關節角θ3和θ4軌跡跟蹤圖(觀測器及參數自適應律開啟與關閉)

圖9 左臂關節角θ1,θ2的三種控制算法軌跡跟蹤圖(關節柔性剛度15 N·m/rad)

3.2 算例2：文中控制算法與奇異攝動法及基于柔性關節補償奇異攝動法的比較

本算例中，在相同關節剛度Ki=15.0 N·m/rad(i=1,2,3,4)情況下，分別采用文中控制算法與基于文獻[14]的奇異攝動法以及基于文獻[18]柔性關節補償的奇異攝動法對雙臂彈性關節空間機器人控制時進行對比仿真，仿真結果如圖8～圖10所示。可以看出，當關節柔性剛度較小時，文獻[18]基于關節柔性補償控制器的奇異攝動控制算法和文獻[14]奇異攝動控制算法在初始階段均無法跟蹤期望軌跡，而文中設計的基于非線性級聯系統的控制算法能夠精確跟蹤期望軌跡。

圖8 載體姿態角θ0的三種控制算法軌跡跟蹤圖(關節柔性剛度15 N·m/rad)

4 結論

空間機器人控制系統設計中若不考慮關節彈性振動，將會對控制精度及穩定性造成很大影響。為此，本文依據非線性級聯系統的概念，設計了一種基于放寬條件改進型NDO的新型自適應動態終端滑模控制算法及力矩反饋控制算法。通過仿真可知：當關節柔性較小時，文中所提出的控制方案可精確完成空間機器人軌跡跟蹤并抑制彈性關節振動，而此時，文獻[14]奇異攝動控制算法基本失效，文獻[18]基于關節柔性補償控制器的奇異攝動控制算法也未能完全精確跟蹤；同時，若沒有對文中機械臂動力學模型式的控制律式(42)進行觀測器估計及自適應動態滑模切換項設計，僅靠非奇異終端滑模控制會大大降低空間機器人的控制精度。