彈性地基中含孔隙的功能梯度圓錐殼的振動分析1)

黃小林 劉思奇 肖薇薇 吳 迪

(桂林電子科技大學建筑與交通工程學院，廣西桂林541004)

功能梯度材料(functionally graded materials,FGM)的板、殼構件已經廣泛應用于航空航天、交通、機械等各種工程領域，研究此類構件的動力特性對其設計有重要的理論意義和工程價值。

迄今為止，FGM圓錐殼的振動問題已引起了一些研究者的關注。Zhang等[1]基于Love的第一近似理論，用廣義微分求積法分析了不同邊界條件下FGM圓錐殼的自由振動，結果發現，除了材料組分指數外，邊界條件、幾何形狀等因素對FGM圓錐殼的基頻也有顯著影響。Nezhadi等[2]基于一階剪切變形理論，研究了FGM圓錐殼在四種脈沖負載類型的沖擊載荷作用下的自由振動和強迫振動，結果表明，對于不同錐角，隨著周向波數的增加，FGM圓錐殼的固有頻率均先減小后增大，且金屬材料在階躍脈沖作用下產生的動力響應最大。

對圓錐殼與彈性地基的相互作用，Sofiyev等[3]用Pasternak雙參數地基模型對彈性地基上FGM圓錐殼的自由振動進行了分析，討論了彈性地基、圓錐殼的大小頭半徑比、材料體積分數等因素對量綱歸一化基頻的影響。結果顯示，Winkler-Pasternak地基對量綱歸一化頻率參數的影響十分顯著。Chan等[4]基于Pasternak雙參數地基模型研究了熱環境中彈性介質包圍的偏心加筋功能梯度截錐殼的自由振動和非線性動力響應，結果發現，隨著彈性地基系數的增大，ES-FGM圓錐殼的振幅值減小，而且Pasternak參數的影響比Winkler參數的大。通過對黏彈性地基上FGM板的振動分析，黃小林等[5]同樣發現Pasternak雙參數中的剪切和壓縮剛度對其振動頻率和動力響應有顯著影響。

在實際工程中，由于材料制備技術的不足，FGM在生產過程中常出現一些孔隙，而這些孔隙對構件力學特性的影響不可避免[6]。Cong等[7]通過研究彈性地基上多孔FGM板在機械、熱和熱機械載荷作用下的屈曲和后屈曲行為，發現孔隙體積分數對多孔FGM板的屈曲和后屈曲的影響顯著。Huang等[8]通過對非線性彈性地基上多孔sigmoid功能梯度板的非線性自由振動和強迫振動的研究，發現孔隙體積分數、線性Winkler參數和Pasternak地基參數對板的最大中心瞬態撓度有顯著影響。Farshid等[9]在彈性地基上雙向功能梯度多孔截錐殼在不同邊界條件下的動力屈曲問題中指出，均勻孔隙系數和不均勻孔隙系數對動力失穩的影響取決于材料梯度指數的大小。他們的研究結果還表明，彈性地基使雙向FGM圓錐殼具有最佳動力性能。文獻[10-12]分別用不同的方法研究含孔隙的FGM板、殼結構的動力響應和動力穩定特性，同樣發現了孔隙的影響不可忽略。

目前關于含孔隙構件的研究都集中于梁和板，對彈性地基中含孔隙的FGM圓錐殼的振動鮮有研究。因此，本文假設FGM圓錐殼由金屬和陶瓷兩種材料構成，考慮孔隙體積不可忽略，根據金屬和陶瓷材料的質量組份計算相應的體積組份，用改進的混合律模型分別計算均勻和非均勻孔隙分布的FGM物性參數，探討孔隙、彈性地基參數、半錐角等因素對FGM圓錐殼自由振動和動力響應的影響，以期為進一步了解FGM圓錐殼動力特性，推廣FGM殼體在相關工程的應用提供理論基礎。

1 基本方程及求解方法

1.1 物性參數

如圖1所示，假設受橫向動載荷q(s,θ,z)作用下的FGM截頂圓錐殼置于彈性地基中，其厚度為h，母線長度為L，半錐角為γ，R1和R2分別為小端和大端的平均半徑，Kw和Kp分別為彈性地基的壓縮剛度和剪切剛度參數。采用右手正交曲線坐標系(s,θ,z)，其中s為母線方向以錐頂為原點的坐標，θ為圓周方向坐標，z為厚度方向坐標(?h/2≤z≤h/2)。圖2給出了兩種孔隙分布類型的FGM圓錐殼截面圖，其中，圖2(a)為均勻分布孔隙，圖2(b)為非均勻分布孔隙。

圖1 彈性地基中含孔隙的FGM圓錐殼

圖2 孔隙分布類型

設Wc和Wm分別表示殼中陶瓷和金屬材料的質量含量，有

兩種組分材料和孔隙的體積含量應滿足

式中，，和α?分別表示整個圓錐殼的陶瓷、金屬和孔隙的體積含量。根據式(1)和式(2)，可計算陶瓷和金屬材料體積含量和分別為

其中，ρc和ρm分別為陶瓷和金屬材料的密度。

考慮孔隙沿圓錐殼厚度方向有均勻和非均勻分布兩種模式，本文非均勻分布類型為常見的沿殼體厚度方向中間孔隙多，頂部和底部孔隙少的情況，因此，其沿殼厚度方向的孔隙率α均勻分布時為

非均勻分布時為

設陶瓷材料體積組分Vc沿厚度方向冪律分布，則

式中，N為材料的組分指數(0≤N≤∞)。根據改進的混合律模型，可計算FGM圓錐殼的彈性模量、密度和泊松比等有效物性參數為

式中，下標c和m分別表示陶瓷和金屬相應的物性參數。由式(5)和式(6)，可得孔隙均勻分布的FGM圓錐殼的物性參數為

孔隙非均勻分布的FGM圓錐殼的物性參數為

1.2 控制方程及求解

假定彈性地基在變形過程中始終與圓錐殼保持接觸，忽略基礎中阻尼和慣性力的影響，地基對圓錐殼的反力為

式中

其中，W為圓錐殼中面的撓度。引入應力函數F，F與殼面內力關系為

為了簡化計算過程，引入下列變換

基于經典薄殼理論，依據哈密爾頓變分原理可導出彈性地基中此圓錐殼的運動方程為

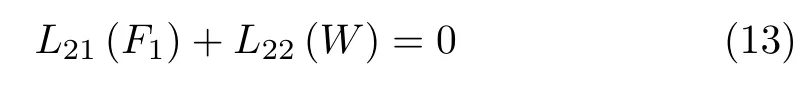
假設殼的兩端為簡支邊界條件，滿足邊界條件的運動方程(12)和方程(13)的解可表示為[13]

式中w(t)為待定函數，m1=mπ/x0，x0=ln(S2/S1)，n1=n/sinγ，m，n分別為沿母線的半波數、沿平行圓的全波數。將式(14)代入式(13)，由諧波平衡法可求得應力函數為

式中，f(t)為待定函數，系數Ki定義見文獻[4]。將式(14)和式(15)代入式(12)，并在式(12)兩邊同乘exsin(m1x)sin(n1φ)，然后在殼內進行Galerkin積分，將系數f(t)用w(t)表示再代入式(12)，得到關于w(t)的二階線性常微分方程組

式中，M和K分別為FGM圓錐殼的廣義質量和剛度系數，且

當q(s,φ,t)=0時，式(16)即為彈性地基上含孔隙的FGM圓錐殼的自由振動方程，令w(t)=ae?wt，代入式(16)，可求得自由振動頻率。當q(s,φ,t)=0時，用Newmark數值積分法可求得橫向動載荷作用下的動力響應。

2 算例比較與參數分析

以下計算實例中，FGM圓錐殼由陶瓷(Si3N4)和金屬(Ni)兩種材料組成，Ni物性參數為Em=205.098 GPa，νm=0.31，ρm=8900 kg/m3，Si3N4的物性參數為Ec=322.27 GPa，νc=0.24，ρc=2370 kg/m3。R1/h=100，L=2R1，量綱歸一化頻率參數

2.1 算例比較

表1將本文計算的FGM圓錐殼的最低量綱歸一化頻率參數與文獻[3]的結果進行了對比。取半錐角γ=π/6。由表1可知，本文的計算結果與文獻[3]接近，最大相對誤差約為3.6%。

表1 彈性地基上兩端簡支FGM截錐殼最低量綱歸一化頻率f的比較

2.2 參數分析

下面分析討論孔隙、材料組分指數、半錐角等因素對兩端簡支邊界條件下FGM截頂圓錐殼振動頻率和動力響應的影響。取模態(m,n)為(1,6)，h=0.01 m，R1=1.0 m，L=2.0 m。

表2計算了不同孔隙率、材料組分指數、彈性地基參數對孔隙為均勻和非均勻分布兩種類型的FGM截錐殼自由振動的影響。取半錐角γ=π/6，陶瓷材料質量組分Wc=0.5。從表中可以看出，當無彈性地基時，含均勻分布和非均勻分布孔隙的頻率均隨孔隙率的增大而降低，且孔隙均勻分布的頻率均比孔隙非均勻分布的要高。這是由于孔隙率的增大一方面削弱了殼的整體剛度引起量綱歸一化頻率降低，另一方面減小了殼的質量而引起量綱歸一化頻率提高，如果孔隙對整體剛度的影響比質量的影響大，則量綱歸一化頻率降低，且孔隙為均勻分布對FGM圓錐殼整體剛度的影響比非均勻分布要大。在彈性地基作用下，含均勻分布孔隙的頻率隨孔隙率的增大而提高，含非均勻分布孔隙的頻率在地基參數(Kw,Kp)=(10 MN/m3，0)條件下，在N∈(0,1]區間內隨著孔隙率的增大而降低，在(1,+∞)區間內隨著孔隙率的增大而提高。在地基剪切參數Kp=10 MN/m3條件下，在N∈(0,0.2]區間內隨孔隙率的增大而降低，在N∈(0.2,+∞)區間內隨孔隙率的增大而提高。正如前所述，當彈性地基壓縮參數和剪切參數為一定值時，兩種孔隙的頻率隨著孔隙率的增大而提高，并且孔隙均勻分布的頻率均比孔隙非均勻分布的頻率要高。這是由于彈性地基強化了殼的整體剛度，若孔隙對殼質量的影響效果比對整體剛度的影響顯著，則引起量綱歸一化頻率提高。從表中還可以看出，量綱歸一化頻率隨著地基壓縮參數Kw、剪切參數Kp的增大而提高，隨著材料組份指數的增大而降低，地基剪切剛度Kp對頻率的影響比壓縮剛度Kw顯著，可見，彈性地基參數的增大強化了圓錐殼的整體剛度。

表2 彈性地基上含孔隙FGM截錐殼的量綱歸一化頻率f的比較

圖3～圖7討論了孔隙率、陶瓷材料質量組分、半錐角等因素對孔隙均勻與非均勻分布的功能梯度材料圓錐殼在s=(S1+S2)/2中面圓周處動力響應的影響。均布突加載荷q=3000 Pa。

圖3顯示了孔隙率α?=0.05，0.1，0.2時孔隙均勻和非均勻分布的動撓度W隨時間t變化的曲線，由圖3可看出，兩種孔隙分布類型的動撓度峰值均隨孔隙率的增大而增大，其中孔隙均勻分布的動撓度隨孔隙率變化更為敏感，并且在相同孔隙率的條件下，孔隙均勻與非均勻分布的振幅值最大相差約35%。

圖4顯示了不同陶瓷材料質量組分對孔隙均勻和非均勻分布的FGM圓錐殼動撓度的影響，從圖4可看出，動撓度峰值隨陶瓷材料質量組分的增大而減小。

圖4 陶瓷材料質量組分對圓錐殼動力響應的影響(γ=π/4,N=2,α?=0.1,Kw=0,KP=0)

圖5給出了三種不同的半錐角對孔隙均勻和非均勻分布的FGM圓錐殼動撓度的影響，從圖中可看出，FGM截錐殼動撓度峰值隨半錐角的增大而明顯增大。

圖5 半錐角對圓錐殼動力響應的影響(N=2,Wc=0.5,α?=0.1,Kw=0,KP=0)

圖6計算了不同彈性地基參數對孔隙均勻和非均勻分布的FGM圓錐殼動撓度的影響，從圖6可分析出，殼體動撓度峰值隨著地基壓縮參數、剪切參數的增大而減小，其中地基剪切參數對殼動力響應的影響比壓縮參數的影響更為顯著。

圖6 彈性地基參數對圓錐殼動力響應的影響(γ=π/4,N=2,Wc=0.5,α?=0.1)

圖7比較了不同材料組分指數對孔隙均勻和非均勻分布的FGM圓錐殼動撓度的影響。從圖7可觀察到，殼動撓度峰值隨材料組分指數的增大而增大。

圖7 材料組分指數對圓錐殼動力響應的影響(γ=π/4,Wc=0.5,α?=0.1,Kw=0,KP=0)

3 結論

本文基于改進的混合律模型及經典薄殼理論，建立了彈性地基中含均勻和非均勻孔隙的FGM圓錐殼的振動方程，求出其在兩端簡支邊界條件下自由振動和動力響應的解析解，計算結果表明：

(1)自振頻率隨地基壓縮和剪切參數的增大而增大，隨材料組分指數的增大而減小，動力響應隨地基壓縮和剪切參數、陶瓷材料質量組分的增大而減小，隨孔隙率、半錐角、材料組分指數的增大而增大。

(2)孔隙對殼自振頻率的影響比較復雜，不僅與孔隙率的大小和分布形式有關，還與材料的質量組分和彈性地基參數有關，與非均勻分布孔隙殼體相比，均勻分布孔隙殼體的自振頻率和動力響應隨孔隙率的變化更為敏感。

(3)增大彈性地基參數或半錐角可有效減小圓錐殼的動撓度，且地基的剪切參數比壓縮參數的影響更為顯著。