靜電紡絲裝置及其力學機理研究進展1)

尹靜 高璐璐 徐 嵐

(蘇州大學現代絲綢國家工程實驗室，江蘇蘇州215123)

靜電紡絲技術是利用高壓電場產生的電場力，激發噴嘴的泰勒錐形成噴射流，并最終獲得納米纖維的一種技術，如圖1所示。這種紡絲技術是生產納米纖維最方便、最直接和最經濟的方法之一，很多聚合物溶液和熔體都可用作原材料以制得納米纖維[1]。該方法已成為開發納米材料的熱點，并開拓了納米纖維的潛在應用，如可將各種離散的納米物質(碳納米管、陶瓷粉等)紡制成連續性納米纖維，從而獲得高性能復合材料。此外，采用靜電紡絲技術生產的納米產品可用于過濾、阻隔、分離膜、服裝材料、生物醫用材料和新型輕質復合材料等，在生物[2]、醫藥[3]、能源[4]、環境[5]、先進制造技術[6]和國防[7]等方面顯示出了巨大的應用前景。

圖1 靜電紡絲原理示意圖

靜電紡絲技術的基本原理在1917年得到首次公布[8]，從1934年Anton Formhals申請了第一項關于靜電紡絲技術的專利[9]，關于靜電紡絲的專利和科技文章的數量越來越多，尤其近十年來發展十分迅速，但是其產業化卻困難重重，問題的關鍵在于靜電紡絲的規模化生產技術和工藝控制問題在根本上影響了其產業化發展道路[10]。目前關于靜電紡絲技術的研究主要側重于各種聚合物的靜電紡絲方法和工藝，而作為解決該問題的關鍵靜電紡絲力學機理的研究相對較少。因此,正確把握靜電紡絲中的各種關鍵因素，建立較為精確完整的力學模型是靜電紡絲機理研究中的基礎問題。本文主要對各類靜電紡絲裝置及其機理研究進行綜合評述，展望靜電紡絲過程中射流力學機理研究的發展前景。

1 靜電紡絲裝置

在研究初期，靜電紡絲裝置中使用的噴絲頭主要為單針頭，紡絲過程中一般產生單股射流，因此設備簡單、操作方便，但其產率低，且射流不可控。隨著靜電紡絲技術的發展，以及對納米纖維批量化的需求，研究者們開始改進和研發各類靜電紡絲裝置，從而實現對納米纖維結構的控制及其產業化。

1.1 單射流靜電紡絲裝置

單射流靜電紡絲裝置指的是紡絲過程中僅能產生單根射流的靜電紡絲裝置。傳統的單射流靜電紡絲裝置如圖1所示，該裝置簡單且操作方便，但是紡絲過程中射流不穩定。功能性納米纖維的出現及其應用需求的擴大，引起了研究者們的日益關注，他們在傳統單射流靜電紡絲裝置的改進方面進行了大量工作，主要集中在以下兩個方面[1]：(1)改進接收裝置，包括附加外場，如電場、磁場、溫度場或流場；(2)改進溶液輸送裝置，包括噴頭部分。

1.1.1 改進接收裝置

通過改進傳統單針靜電紡絲裝置的接收裝置可以獲得有序納米纖維、具有多孔結構的納米纖維和大孔徑的納米纖維，如圖2所示。

圖2 納米纖維電鏡圖(續)

圖2 納米纖維電鏡圖

有序納米纖維能更好地應用于細胞定向培養、傳感器、光電子元件以及組織工程支架等領域[11]，其制備方法主要分為三類，一類是平行電極法[12-13]，如圖3(a)所示，將兩塊平行放置的導電板作為接收裝置，由于導電板之間電場力的作用，使得納米纖維有序排列在導電板之間，從而獲得有序納米纖維；一類是轉軸法，如圖3(b)所示，采用接地的旋轉接收裝置，如圓盤形[14]、圓柱形[15]和平行間隔排列的銅線轉輪[16]等，通過旋轉裝置對射流的物理牽伸作用獲得有序納米纖維；一類是外加電場[17-18]或磁場[19-20]法，如圖3(c)和3(d)所示，通過附加的電場或磁場來控制射流的運動軌跡，從而獲得有序納米纖維。

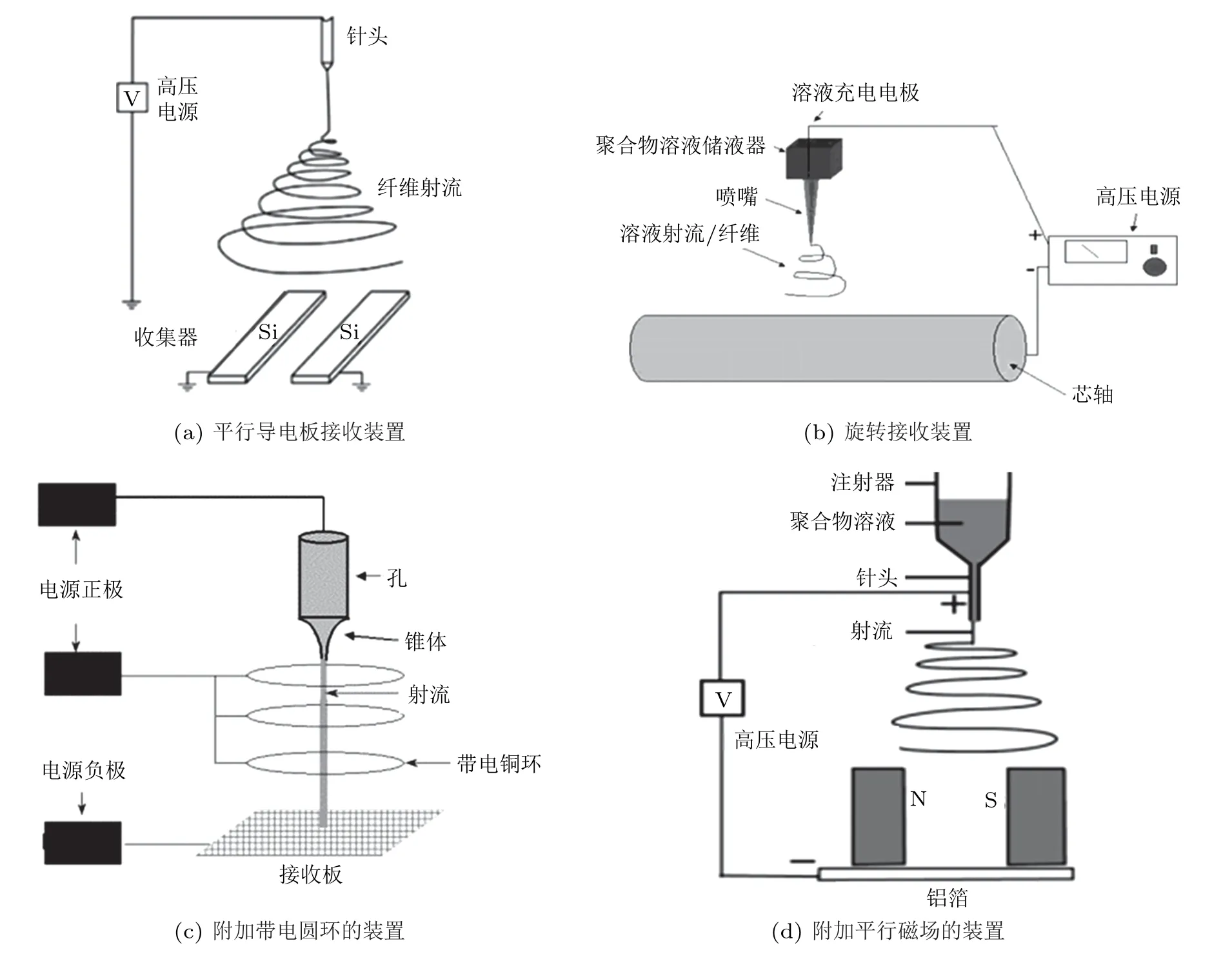
圖3 制備有序納米纖維靜電紡絲裝置示意圖

超高比表面積的具有多孔結構的納米纖維具有更高的吸附、滲透、光電及生物活性等特性，可廣泛應用于吸附及分離介質、光電材料、生物醫學等領域[21]，其制備方法主要是促使靜電紡絲過程中的射流發生快速的相分離，從而使纖維具有多孔結構。Mccann等[22]將浸入液氮浴中的接地硅晶片或鋁箔作為接收裝置，如圖4(a)所示，液氮浴將導致聚合物和溶劑間的相分離，從而獲得具有多孔結構的纖維；本課題組[23]采用具有加熱裝置的接收板來獲得多孔結構的納米纖維，如圖4(b)所示；Fashandi等[24]設計了一個溫濕度調節箱，如圖4(c)所示，它通過調節氣流的溫濕度來控制納米纖維多孔結構的形成。

圖4 制備多孔納米纖維裝置示意圖

大孔徑納米纖維膜的纖維之間具有較大的孔隙，有利于營養物質傳輸和廢棄物排泄，從而促進細胞生長，可以更好地應用于組織工程領域[25]。Blakeney等[26]將有不銹鋼探針嵌入的半球形圓盤作為接收裝置，如圖5(a)所示，制備了三維棉球狀大孔徑納米纖維支架，此支架上種植的細胞會滲透到其中，且細胞生長速度有所提升；Vaquette等[27]研究了接收裝置幾何形狀對纖維取向和纖維支架結構的影響，如圖5(b)所示，發現纖維網孔徑的增加可促進細胞的增殖和遷移；劉桂陽等[28]采用帶孔的金屬滾筒作為接收裝置，如圖5(c)所示，收集具有取向性的大孔結構纖維網；本課題組[29-30]將銅網和置于其后的氣泵作為接收裝置，如圖5(d)所示，通過調節銅網尺寸和風速等參數來制備大孔徑納米纖維膜。

圖5 大孔徑納米纖維制備裝置

1.1.2改進溶液輸送裝置

對靜電紡絲裝置的溶液輸送裝置進行改進主要是期望得到具有空心、核殼和多層結構的納米纖維，如圖6所示，它們在藥物緩釋和組織工程等領域具有良好的應用前景[31]。目前，制備這些納米纖維的主要方法是將溶液輸送裝置改進為二級同軸噴絲頭[32]或三級同軸噴絲頭[33]，如圖7所示。

圖7 同軸靜電紡絲裝置示意圖

1.2 多射流靜電紡絲裝置

單射流靜電紡絲裝置生產的納米纖維產量低，難以滿足各種應用需求，因此能夠實現批量化制備的多射流靜電紡絲裝置成為了研究熱點。目前，多射流靜電紡絲裝置主要分為兩類，即多噴頭靜電紡絲裝置和無噴頭靜電紡絲裝置。

1.2.1 多噴頭多射流靜電紡絲裝置

多噴頭靜電紡絲方法是增加射流數量以提高納米纖維產量的有效方法之一，也是納米纖維工業化生產的發展方向之一。多噴頭靜電紡絲裝置中的多個噴頭一般以一定陣形排列[34-35]，如直線形、圓形、橢圓形等，如圖8(a)所示，研究發現該類裝置可提升射流量，進而使紡絲產量增加，纖維的產量與針頭數量成正比[34]，但各射流表面的電荷所產生的庫侖力會對射流路徑產生影響，圓形排列生產出的納米纖維質量最好，直線形排列的纖維質量最差[35]；楊責重等[36]在裝置的環形儲液管道上設有許多呈環形陣列分布的針頭，且均指向環形管道中心的滾筒接收裝置，如圖8(b)所示，可大大提升產量。然而，這些多針頭靜電紡絲裝置在其紡絲過程中由于相鄰針頭之間會產生電場的相互干擾，這不僅直接影響紡絲過程，而且會影響納米纖維的性能，因此出現了在針頭外圈添加輔助電極來克服這種缺陷的方法[37-38]，如圖8(c)和圖8(d)所示，可有效減少紡絲過程中射流所受的干擾，從而減輕射流不穩定性，增加纖維產量。

圖8 多針頭靜電紡絲裝置示意圖

1.2.2 無噴頭多射流靜電紡絲裝置

盡管多噴頭可以提高靜電紡納米纖維的產量，但在這一過程中仍存在針頭堵塞、射流相互作用等問題。因此，近年來出現了許多無噴頭靜電紡絲方法來獲得高產量的納米纖維，它們均是利用高壓電場在自由液體表面自發形成射流的紡絲方法，其裝置的改進主要在于噴絲裝置(即儲液裝置)的改進。Yarin等[39]在帶有永磁體的噴絲裝置中的下層放置磁懸液，上層放置聚合物溶液，如圖9(a)所示，其受法向磁場作用，磁懸液的垂直尖峰擾動了層間界面以及最上層聚合物層的自由液面，當外加電場時，自由液面的擾動受到電場的強烈拉伸產生多股射流；Thoppey等[40]采用碗狀噴絲裝置和同心的圓柱形接收裝置進行紡絲，如圖9(b)所示，在高電壓下，射流在自由液面上自發地形成，并沿著碗狀噴絲裝置的圓周邊緣排列；Jiang等[41]使用階梯式金字塔形銅噴絲頭進行靜電紡絲，如圖9(c)所示，紡絲時，噴絲頭的邊緣同時形成多個射流；于昊楠[42]設計了一種碟形噴頭的靜電紡絲裝置，如圖9(d)所示，實驗表明，圓周傾角為60°的碟形噴頭，批量化生產最為合適。本課題組首先根據氣泡動力學原理提出了可批量生產納米纖維的氣泡靜電紡絲技術，該技術采用高壓靜電和外加氣流等作為動力來克服氣泡的表面張力，從而產生多股射流，如圖9(e)所示[43]；接著在此基礎上，將錐形聚合物噴嘴和銅質儲液裝置相結合，提出了一種更高效制備納米纖維的噴氣靜電紡絲技術，并采用轉鼓作為接收裝置，用來批量制備有序納米纖維，如圖9(f)所示[44]；最后，對紡絲裝置進行了進一步改進，設計了三種不同的噴絲裝置，如圖9(g)所示，分別為具有圓柱切面(g1)、斜切面(g2)和球切面(g3)的噴絲裝置，結果表明球切面噴絲裝置紡絲效果最好[45]；同時，應用斜切面噴絲裝置批量制備了用于傷口敷料的納米纖維膜[46]。

圖9 自由液面靜電紡絲裝置

2 射流形成機理

在靜電紡絲過程中，帶電的聚合物溶液在電場力的作用下沿毛細管運動，聚集在噴絲口處形成聚合物液滴；當電場力足夠大時，液滴克服表面張力形成噴射流。在噴射過程中，射流中的溶劑蒸發或其自身發生固化逐漸成為纖維，最終落在接收裝置上。自靜電紡絲技術出現以來，許多研究者已經對影響射流形成的主要因素進行了分析，如施加電壓和溶液性質等。

Taylor[47]于1969年發現了在電場力的作用下毛細管尖端的黏性液滴形成泰勒錐(Taylor cone)并產生射流的情況，并首次用數學表達式描述了液滴在毛細管口的平衡狀態，建立了產生噴射流的臨界電壓近似表達式，即

其中Vc為電壓，H為噴絲口到接收板的距離，L為噴絲口的長度，R為噴絲口半徑，γ為溶液的表面張力；Hendrick等[48]采用高速攝像機研究了不同壓力下毛細管尖端的下垂半球形液滴形成射流的機理，并推導出了射流形成的臨界電壓與表面張力間的關系式；Ying等[49]研究了產生泰勒錐的位置對形成射流的影響，及其對獲得的纖維直徑的影響，發現產生的泰勒錐部分在噴嘴外部時，形成的射流角度較小且纖維直徑最均勻。

3 射流運動規律

靜電紡絲過程中，射流先呈直線運動，在運動到一定距離后開始變得不穩定并發生振蕩，然后在此不穩定狀態下，射流最終被振蕩拉伸為纖維，因此射流的運動過程可分為兩個階段，如圖10所示，即射流穩定運動階段和射流不穩定運動階段[50]。

圖10 射流運動規律示意圖

3.1 射流的穩定運動階段

射流的初始運動即射流的穩定運動階段(長度通常<1 cm)對聚合物分子鏈的拉伸起著重要作用[51]，同時也影響射流不穩定運動階段及最終的纖維直徑。He等[52]經過計算分析得出射流直線運動的臨界長度L，即

其中，k為流體的無量綱電導率，Q為紡絲流量，ρ為流體密度，I為電流強度，R0=[2σQ/(πkρE)]1/3,σ為表面電荷密度，E為電場強度，r0為噴絲孔半徑。Rutledge等[53]發現穩定射流長度L依賴于射流表面電荷密度和局部電場強度，在此基礎上建立了其計算公式，即

其中，K為表面電荷密度，x為射流長度與初始射流的內徑的比值，E∞為所施加的電場強度，ˉε為射流表面的介電常數；Lei等[54]提出了穩定射流長度與最終纖維半徑之間的關系模型，即rf，其中，rf為最終纖維半徑，Lsj為穩定射流長度；此外，一些研究利用靜電紡絲射流的穩定運動階段，提出了低壓近場靜電紡絲技術，通過將接收距離控制在幾厘米或幾毫米范圍內來精準控制纖維的沉積位置，從而制備圖案可控的纖維膜[55-56]。

3.2 射流的不穩定運動階段

射流在經歷穩定運動階段后，在電場力、重力、空氣阻力、射流表面張力及其內部黏彈力等作用下，進入不穩定運動階段，其可決定纖維的直徑及最終形態。射流的不穩定運動主要有三種[57]：軸對稱不穩定、彎曲不穩定和鞭動不穩定，此外還有噴絲的不穩定性，即劈裂、分叉等現象[58]。射流的不穩定運動是制約靜電紡絲發展的一個重要因素，因此，如何抑制射流的不穩定運動得到了不少研究者的關注。

Zuo等[59]發現高導電率的溶液可增加射流的電荷密度，抑制射流的軸對稱不穩定性，但會加劇射流的鞭動不穩定性；Kong等[60]發現紡絲電壓較低時，射流彎曲不穩定性影響顯著，導致射流拉伸不充分且隨機沉積，而在電壓較高時，射流拉伸較充分且可定向沉積，但易發生劈裂、分叉等現象，如圖11所示；本課題組[61]研究了磁場的加入對射流的不穩定運動的影響，發現磁場的加入可抑制射流的不穩定性運動；袁卉華等[62]則通過調節紡絲溶液的黏彈性，實現抑制射流不穩定彎曲擺動，從而使聚合物分子鏈得到持久牽伸，導致取向和微晶的形成；王文[63]通過模擬研究得出接收距離的減小將導致射流不穩定區域縮小，即鞭動區域減小，但射流無法充分拉伸使得纖維直徑增大；Dharmansh等[64]考慮了射流半徑、速度、電場和表面電荷密度沿軸向的變化，提出可通過降低紡絲液電導率和表面張力或提高其黏度來抑制軸對稱不穩定運動的形成，從而抑制串珠的形成；林燦然等[65]研究發現添加平行輔助電極后，射流的鞭動效應受到平行電場的抑制，纖維發生卷曲的幾率減小；Li等[66]引入輔助圓環電極，并研究其電壓對射流的影響，發現圓環電極的電壓越大，射流的鞭動不穩定性越大。

圖11 靜電紡絲射流的不穩定性[60]

4 靜電紡絲力學模型

靜電紡絲的整個過程行為非常復雜，迄今其中某些作用機理都沒有被完全解釋清楚。這不僅使得靜電紡絲技術的理論完善困難重重，同時也阻礙了靜電紡絲技術的發展。因此,正確把握靜電紡絲中的各種關鍵因素,建立較為精確完整的力學模型是解決該問題的關鍵，一直受到各相關領域的關注。

4.1 靜電紡絲過程中單相射流的模型建立

靜電紡絲過程中，射流的形成主要依賴于電場力的施加，電場的大小決定了纖維最終的形態。Fang等[67]通過實驗建立了電壓(E)、表面張力(γ)、空氣介電常數(ε0)和射流半徑(R)之間的數學表達式，即Rutledge等[68]根據實驗研究結果建立了振蕩射流模型，認為射流的最終直徑(r)僅與流速(Q)、電流(I)和表面張力(γ)有關，即r=c(I/Q)?2/3γ1/3(c為常數)；Theron等[69]對靜電紡絲過程中的紡絲參數進行了實驗研究，并根據實驗數據建立了一系列的經驗公式。然而，這些研究都是基于實驗研究獲得的經驗公式，具有很大的局限性。因此，為了得到較為完善的、具有指導意義的靜電紡絲模型，研究者們開始應用力學方法對靜電紡絲過程進行全面深入的研究。

Spivak等[70]對靜電紡絲穩定射流建立了一個簡單的力學模型，即Spivak-Dzenis模型，其動量守恒方程僅考慮了黏性力與電場力的作用；Feng[71]建立了簡單的一維非牛頓流體模型，但其對靜電紡絲過程中的影響因素考慮不全面；Fridrikh等[72]通過理論研究建立了表面張力(γ)、流速(Q)及電流(I)等紡絲參數對靜電紡絲過程影響的模型，即

其中，h為射流末端半徑，ˉε為外部介質常數，χ為不穩定波長。此模型可用于預測最終獲得的纖維直徑，但較為復雜，在實際應用中存在較大困難；He等[73]采用標度率分析方法對電荷守恒方程進行了理論分析，建立了靜電紡絲過程中的電流與電壓的標度率關系，即(式中，I為通過高聚物射流的電流，E為紡絲電壓，α為不同高聚物的待定參數)。張健宗[74]結合質量守恒和動量守恒定律，得到穩定射流段的受力平衡方程，即

式中，p為液體的內部壓強，u為流速，ρ為電荷密度，E為施加的電場，τ是黏性力，σ為電荷密度。原波等[75]對靜電紡絲纖維拉伸形成過程進行建模，采用表面效應理論建立了微觀力學模型，即Eeff=E(1+4ls/D)(Eeff為等效模型，E為電場力，ls表示受力模型表面模量與體模量的比值，D為纖維直徑)，其可解釋纖維拉伸變形中的尺度效應；Zheng等[76]建立了電場力與射流速度之間的模型，即E=??V，?·(ε0εr?V)=ρv(V為電壓，ρ為空間電荷密度，v為射流速度)，但其模型只能預測射流的直線速度，對于彎曲部分的速度還需進一步研究；盧錦煜等[77]對帶電射流不穩定段進行了力學分析，包括對重力、電場力、庫侖力、黏彈性力、表面張力和空氣阻力進行分析計算，并在受力分析的基礎上建立了三維笛卡爾坐標系下帶電射流理想行為的耦合控制方程。

在上述建立的傳統靜電紡絲力學模型基礎上，研究者們還對一些功能性納米纖維的制備過程進行了理論研究。Rafiei等[78]綜合考慮了影響核殼結構納米纖維質量的有效參數，如射流的直徑及流速、電場、核層與殼層溶劑性質等，建立了核殼結構射流的力學模型，并推導了核殼結構射流在任意時間階段的直徑計算公式；本課題組[79]研究了靜電紡多孔納米纖維的孔結構形成原理,發現紡絲過程中溶液揮發吸熱引起了靜電射流中熱不穩定，進而引起相分離，導致纖維多孔結構的形成，并應用了文獻[80]中的模型修正方法，考慮溶液揮發吸熱的影響，對靜電紡絲力學模型進行了改進和修正；此外，本課題組[81]還應用伯努利方程研究了靜電紡制備多孔納米纖維過程中的主射流劈裂生成分射流的現象，發現纖維上的多孔結構會隨著劈裂的產生發生變化，劈裂前后纖維上的孔結構變化明顯。

4.2 多場耦合作用下單相射流的力學模型

隨著靜電紡絲技術的發展，出現了在紡絲過程中施加輔助電場、磁場、氣流場及熱場等影響射流運動的方法，因此建立多場耦合作用下的射流模型是十分必要的。

Ko等[82]通過修改Maxwell方程、受電場影響的熱流體的N-S方程和流體本構方程建立了一個較完善的熱?電?射流單相流模型，但其模型非常復雜，很難進行實際應用；萬玉芹[83]在此基礎上，考慮了電、熱效應的影響，對Spivak-Dzenis模型進行了改進，所構建的一維帶電射流微元體的受力主要包括黏性阻力、重力、電場力、極化力及溫度梯度力，從而得到了一個改進的一維靜電紡絲模型；吳玥[84]對在靜電紡絲過程中引入磁場的紡絲方法進行了研究，通過對射流的受力分析，發現磁場的引入使射流的擺動幅度得到控制，并推導出了引入磁場前后的射流擺動與軸向距離之間的關系。本課題組[28]在上述模型的基礎上，考慮電場、磁場、振動力場和流場耦合的作用，建立了一個較為精確完整的多場耦合作用下的靜電紡絲模型，如下所示：

(1)Maxwell方程組

其中，qe是電荷量，E是電場強度，J是電流，B是磁感應強度，H是磁場強度，D是原子位移矢量，c是真空中的光速。

(2)連續方程

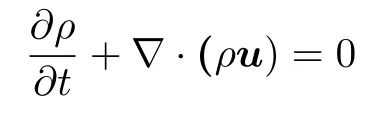
其中，ρ是射流的密度，u是射流速度。

(3)動量方程

其中，t是應力張量，f是體積力，P是極化度，Fm為磁場作用力，Fv為振動力場作用力，Ff為氣流流場作用力。

(4)能量方程

其中，cp為定壓比熱容，Qh是源項，q是熱量，M為磁化強度，Qf是空氣摩擦阻力產生的能量損失。

Deshawar等[85]研究了熔體靜電紡絲過程中溫度(T)對紡絲過程的影響，特別是其對流體黏度(η)的影響，并建立了熱能守恒方程及黏度表達式，即

其中，PeT為Thermal P′eclet數，Na為Nahme-Griffith數，BiL為Biot數，T∞為環境溫度，Ea為無量綱的活化能。其他參數具體含義可詳見參考文獻，下同。

4.3 多場耦合作用下的多相射流力學模型

在上述靜電紡模型的研究中，都只對單相射流進行了研究，難以準確描述靜電紡過程中射流的運動軌跡，因此建立一個完善的多場耦合作用下的多相流模型對于理解和掌握靜電紡絲技術是十分必要的。本課題組[86]在已建立多場耦合作用下的單相射流模型的基礎上，考慮不溶于溶液的顆粒的分散與溶劑的揮發，建立了多相流模型，此模型采用流體體積函數法來確定自由表面，即?(αqρq)/?t+?·(αqρuq)=采用離散相法獲得離散相(顆粒)的運動軌跡，即

其中，uq和αq分別是第q相的速度矢量和體積分數，p和q是相指數，˙mpq(˙mqp)是從第p(q)相到第q(p)相的傳輸質量，μ為流體黏度，dp為顆粒直徑，CD為阻力系數，Re為相對雷諾數，u為流體相速度，up為顆粒的速度，ρ為流體的密度，ρp為顆粒的密度，F為附加力(梯度壓力、溫度，參考系的轉動力等)。

在此基礎上，本課題組[81]根據文獻[87]中提出的湍流纖維懸浮模型建立了改進的顆粒懸浮模型，并用于研究靜電紡納米懸浮體過程中的力學機制。此模型如下所示

其中，ρp為粒子的密度，?為粒子的體積分數，ˉup為粒子相的平均速度，τp為顆粒對流體應力的貢獻，˙γ為剪切速率，Q為張量參數。

靜電紡絲過程是非常復雜的，要想對其復雜流動的詳細多尺度結構進行研究，需要在已建立的模型基礎上，對靜電紡絲過程進行數值模擬研究。

4.4 電場作用下的紡絲過程的數值模擬

Reznik等[88]對靜電紡絲過程中的液滴形狀變化進行了數值模擬研究；王文[63]使用Comsol Multiphysics(CM)軟件對單針頭靜電紡絲過程中電場強度分布進行了數值模擬，并研究了電壓大小、針管長度、直徑、接收距離對其的影響；Rafiei等[78]使用FeniCS軟件模擬了核殼結構納米纖維在電場作用下的直徑變化，并與相同紡絲條件下的實驗結果進行了對比；Hashemi等[89]提出了在均勻外加電場和穩定的錐射流模式下的牛頓流體行為的數值模型，并對初始射流進行了建模與仿真；Jin等[90]采用有限元法對靜電紡納米纖維紗線過程中的電場分布進行了模擬,并研究了電場分布和電場強度對獲得的納米纖維表面形貌、機械性能、熱性能和吸水性能的影響；李想[51]通過CM軟件模擬噴嘴附近和外部的電場研究了不同噴嘴結構對纖維的影響，發現噴嘴出口處的電場主要影響纖維分子鏈的拉伸與取向，而鞭動部分的電場主要影響纖維直徑的拉伸；Liu等[91]采用Maxwell 2D軟件數值研究了電壓大小對單針紡絲射流數量的影響，如圖12所示，其數值模擬結果與實驗結果相符，發現在低電壓下僅在泰勒錐的尖端產生一個射流，而隨著電壓值增大超過臨界值后，針管邊緣將產生多個射流；Zhu等[92]采用CM軟件數值研究了梯形陣列下針尖尺寸和介質材料對紡絲過程中電場分布的影響，實現了高密度布置多針頭時電場分布的均勻性；本課題組[93]則使用Maxwell 3D軟件數值研究了自由液面靜電紡絲過程中球切面儲液裝置的半徑大小對其電場分布的影響，并應用曲面響應法確定了儲液裝置的最優紡絲半徑。

4.5 多場耦合作用下的紡絲過程的數值模擬

對于在靜電紡絲過程中施加外場來提高紡絲效果以及獲得有序納米纖維的紡絲方法，研究者們也對其開展了數值模擬研究，大多數研究集中在靜電紡絲過程中引入輔助電極的方法上。Deitzel等[16]對于制備取向納米纖維的紡絲方法進行了數值研究，該方法在針頭與接收板間附加金屬導電圓環，研究發現導電圓環使射流的鞭動現象減弱；Liu等[94]采用ANSYS軟件模擬計算了紡絲裝置周圍的電場強度，研究了接地的細長狀輔助電極的位置、長度和直徑對納米纖維質量和產量的影響，模擬結果顯示輔助電極的引入提高了紡絲電場強度；Wu等[95]采用CM軟件研究了施加電壓大小與針頭處放置垂直或平行的接地輔助電極對電場強度的影響，發現電壓越高電場強度越大，且平行位置的輔助電極可較好地增加針頭處的電場強度；Li等[66]應用Maxwell 3D軟件數值模擬了紡絲過程中有無輔助圓環電極時的電場分布，如圖13，結果顯示輔助電極的添加使得電場聚焦于射流運動區域。

圖13 添加輔助圓環電極前(a)和(c)后(b)和(d)電場分布[66]

Campatelli等[96]采用有限元法模擬多針頭靜電紡絲過程，分析了電壓大小以及針頭與接收裝置和輔助電極的距離對射流的發散角度、射流長度的影響；Chen等[97]為解決多針靜電紡絲針頭處電場不均勻性，提出了一種平行輔助電極來增強多針頭上的電場，并采用CM軟件對改進的紡絲裝置進行了電場的數值模擬與分析，從而設計了均勻電場；王巍等[98]應用CM軟件研究了無針式靜電紡絲裝置的噴頭形狀及其附加的平行片狀輔助電極對紡絲過程中電場分布的影響，發現噴頭為圓柱體時電場強度最大值出現在兩端，附加助電極后，圓柱體兩端的電場強度減弱，而對于階梯狀噴頭，輔助電極的加入可以明顯改變中間區域的電場分布。

此外，研究者們還對附加其他外場(如磁場和氣流場)的靜電紡絲方法進行了數值研究。本課題組[99]分別在無磁場和有磁場的情況下，應用MATLAB軟件對已建立的單相流模型進行了初步的數值計算，結果表明磁場對噴射流的不穩定性具有明顯的控制作用；Liu等[100]采用有限元法數值模擬了具有不同形狀的氣體通道的氣泡靜電紡絲裝置的紡絲過程，計算結果表明從泰勒錐形狀的氣體通道出來的氣流對泰勒錐的產生和納米纖維的形成有促進作用；Kwon等[101]采用CM軟件數值模擬了氣流輔助多噴嘴熔體靜電紡絲過程，研究了多噴嘴陣列(噴嘴數量和噴嘴間的距離)及外加電壓對電場分布的影響，結果表明電場強度隨噴嘴數量和噴嘴之間的距離的增加而減小，隨外加電壓的增加而增加。

4.6 多場耦合作用下多相流的紡絲數值模擬

上述數值研究均只對單相射流進行了研究，而缺少對于含有氣泡或顆粒的多相射流的數值研究。Lee等[102]采用CM軟件模擬了兩種聚合物溶液在同軸靜電紡絲噴嘴中的流體行為，并研究了同軸靜電紡絲過程中兩相射流的穩定狀態；Saja等[103]采用CM軟件數值研究了靜電紡絲過程中兩相流(納米硅與聚丙烯腈溶液)中的硅顆粒分布，其實驗結果與模擬結果一致，表明較大的硅顆粒遷移速度較快且具有較高的慣性力，使其遷移至射流外層，且顆粒的遷移速度隨著粒子的尺寸減小而減小；Yousefi[104]應用Kelvin-Voigt模型數值模擬了含有間隔顆粒的靜電紡絲射流，對射流的運動軌跡進行了預測，并研究了間隔顆粒的存在對納米纖維復合結構的厚度與孔隙的影響；而本課題組[105]則在已建立的多場耦合作用下的兩相流模型的基礎上對紡絲過程中射流的運動軌跡進行了數值模擬，其數值結果與實驗結果相一致，表明該方法可用來預測此射流流動；本課題組[106]還對靜電紡絲過程中含有Fe3O4納米顆粒的固液兩相流進行了數值模擬，模擬結果與實驗數據吻合較好，表明加入Fe3O4納米顆粒后，紡絲溶液的導電性提高，射流速度增加，納米纖維直徑減小；此外，本課題組[107]對單氣泡靜電紡絲過程中的射流進行了數值模擬，并與通過攝像儀獲得的射流形態進行了比較，如圖14所示。

圖14 氣泡靜電紡絲過程數值模擬結果與試驗結果

5 展望

目前關于靜電紡絲技術的裝置、工藝和機理等各方面的研究越來越多，尤其近十年來發展十分迅速，但使其商業化卻困難重重，問題的關鍵就在于缺少完善的力學模型和符合實際的數值研究，這嚴重影響了靜電紡絲的規模化生產及其設備的開發。隨著對靜電紡絲理論研究的逐步深入，許多已建立的模型和進行的數值模擬不是限制條件過多(如不等壓、等溫和簡單流變模型等)，就是借助于簡化的實驗模型，大多都無法指導實際生產。因此，本文認為靜電紡絲未來的發展主要在兩個方面：(1)建立完善的靜電紡絲力學模型，發展可指導實際生產的數值研究方法，為實現納米纖維的批量制備提供充分的理論依據；(2)設計和制造新型靜電紡絲設備，實現納米纖維的規模化生產及其商業化應用。