結構化Krylov-SVD分解的顯著性目標檢測算法
鄭維佳,張榮國,胡 靜,趙 建,劉小君
(1.太原科技大學 計算機科學與技術學院,山西 太原 030024;2.合肥工業大學 機械工程學院,安徽 合肥 230009)
0 引 言
顯著性目標檢測在圖像處理領域應用廣泛,如目標檢測[1]、基于內容的圖像檢索[2]和圖像壓縮和重定位[3-4]。
現有的顯著性模型大致分為兩類:生物模型和計算模型。生物學模型通常是要找到一些最能引起人們注意的點,因此所得的顯著圖通常是稀疏且模糊的,并限制了它們的應用范圍,主要用于預測眼球注視。相反,受生物模型啟發的計算模型旨在發現從周圍區域突出的物體。目前的計算模型主要分為有監督的自上而下的顯著性目標檢測[5]和無監督的自下而上的顯著性目標檢測[6]。最近,一些研究人員將自上而下的高級先驗與自下而上的低級圖像特征相結合,并引入到統一的顯著性目標檢測框架。其中具有代表性的方法是將低秩矩陣恢復理論應用于顯著性目標檢測[7-9]。現有的基于低秩矩陣恢復的顯著性目標檢測模型通常將圖像分為兩個部分:高度冗余的圖像部分(背景區域)和稀疏的顯著部分(前景區域)[10]。這些方法可以計算給定圖像的顯著圖并檢測顯著目標,但是它們通常假設稀疏矩陣中的每個元素是獨立的,而忽略了它們之間的潛在關系和結構,導致生成的顯著圖出現發散或不完整現象。
為解決這些問題,Peng等人[11]提出結合低秩和結構化稀疏矩陣分解模型(SMD),然而該模型仍然沒有解決迭代導致的高計算復雜度問題,從而限制了該模型在大規模特征矩陣應用中的可擴展能力。針對上述問題,文中提出基于無監督的低秩恢復顯著性檢測算法,該算法的關鍵思想在于:(1)提出了Krylov-SVD算法利用奇異值分解(SVD)對大型稀疏矩陣求前k個特征值的精確解;(2)提出了樹形結構稀疏誘導范數來約束前景矩陣S,換句話說,先前的研究對前景矩陣中的元素默認為是相互獨立、互不影響的,因此忽略了圖像像素或圖像塊之間空間上的連續性和模式上的相似性。這就導致了模型產生的前景是離散的,不連續的,支離破碎的。為了評估算法的顯著性檢測性能,引入MSRA10K[12]、SOD[13]和ECSSD[14]三個數據集,并和現有的十一種算法進行對比。實驗結果表明,文中提出的基于結構化低秩矩陣Krylov-SVD分解的顯著性目標檢測算法在顯著性目標檢測方面有良好表現。
1 Arnoldi模型理論基礎
低秩表示為圖像處理提供了新的思路和新方法。隨著低秩表示在圖像處理方面的深入研究,現代迭代子空間方法中Arnoldi方法是最典型的一類適用于計算大型低秩非對稱矩陣的Krylov子空間法。
給定具有如下形式的線性時不變系統:
(1)
其中,a∈Rn×n是常系數矩陣,b,c∈Rn是常數向量,x(t)∈Rn是系統的狀態變量,u(t)∈R是系統的輸入變量,y(t)∈R是系統的輸出變量。假設線性時不變系統的初始狀態為零,通過拉普拉斯變換后得到傳遞函數為H(s)=cT(sI-a)-1b。任取s0∈C,使得s0I-a非奇異。作變換s0=s0+σ,令:
F=-(s0I-a)-1,l=(s0-a)-1b
則線性時不變系統(1)可變為如下系統:
(2)
其傳遞函數為H(σ)=cT(I-σF)-1l。
設V=(v1,v2,…,vr)(rn)是由F及l應用r步傳統Arnoldi算法得到的標準列正交矩陣,則Q構成Krylov子空間Kr(F,l)的一組基,即:
Kr(F,l)=span{l,Fl,…,Fr-1l}=colspan{Q}
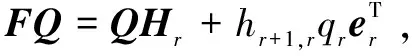
以Q作為變換矩陣,可得到線性時不變系統(2)的降階系統。
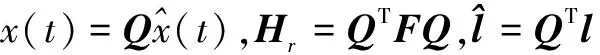
由于Arnoldi算法只涉及矩陣與某些向量的乘積,因此可充分利用矩陣的稀疏性和其結構特征對其特征值進行求解,Krylov-SVD重啟方法就是在此方法的基礎上結合奇異值分解技術提出的[15-16]。
2 結構化Krylov-SVD分解的低秩矩陣表示
2.1 低秩矩陣的Krylov-SVD分解
Shen等人[17]將輸入圖像的特征矩陣F粗略看作是一個低秩矩陣L加上一個稀疏矩陣S,即F=L+S,通過解這一模型來獲取顯著性目標,即:
(3)
式中,rank(?)表示矩陣的秩函數,秩函數是一個NP難問題,為解決式(3)問題通常將求解秩函數轉化為核范數的求解,并利用矩陣奇異值之和來求解該核范數,即:
假設輸入圖像I被劃分為n個非重疊超像素P={P1,P2,…,Pn}。從每個塊Pi中提取一個D維特征向量Ii∈Rm,則I可以由n個特征向量表示為F={I1,I2,…,In}∈Rm*n。利用Krylov-SVD分解可以將特征矩陣F分解為低秩矩陣L和稀疏矩陣S。
設F∈Rm*n特征矩陣的奇異值分解為:
UTFV=diag(|λ1|,|λ2|,…,|λn|)
其中,U∈Rn*n、V∈Rn*n是正交矩陣,且F的奇異值滿足|λ1|≥|λ2|≥…≥|λn|。
令:
V=Udiag(ε1,ε2,…,εn)
計算出UTV的對角矩陣diag(ε1,ε2,…,εn),其中:
由對稱矩陣的譜分解及其奇異值分解之間的關系可推出:對實對稱矩陣而言,其奇異值就是其特征值的絕對值。可得F的特征值為:
λ(T)=diag(|λ1|,|λ2|,…,|λn|)*diag(ε1,ε2,…,εn)=diag(λ1,λ2,…,λn)
設λ(T)是SVD分解的標準型對角矩陣,其中T=diag(|λ1|,|λ2|,…,|λr|),式中u∈Rr*r、v∈Rr*r是正交矩陣,且:
v=udiag(ε1,ε2,…,εr)
其中:
則由λ(T)=(λ1,λ2,…,λr)*(ε1,ε2,…,εr)計算正交矩陣U2∈Rr*r,使得:
式中,λ(T1)=(λ1,λ2,…,λk)*(ε1,ε2,…,εk),j=1,2,…,k,即λ(T1)的特征值均位于主對角線上且按降序排列。
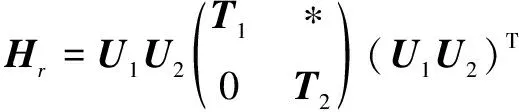
取其兩端前k列可得:
(4)
通過Householder變換計算正交矩陣Q∈Rk*k,使得QTT1Q=Hk。經式(4)計算可得圖像背景低秩矩陣L,即:
L=Q×H
2.2 結構化Krylov-SVD分解的低秩矩陣表示


圖1 基于超像素構造的索引樹
基于預定義的索引樹,加權結構化稀疏范數定義為:

基于結構化低秩矩陣Krylov-SVD分解的顯著性目標檢測具體算法步驟如下所示:
輸入:從給定圖像數據集中選取一幅圖像;
輸出:經算法處理后的顯著性圖像。
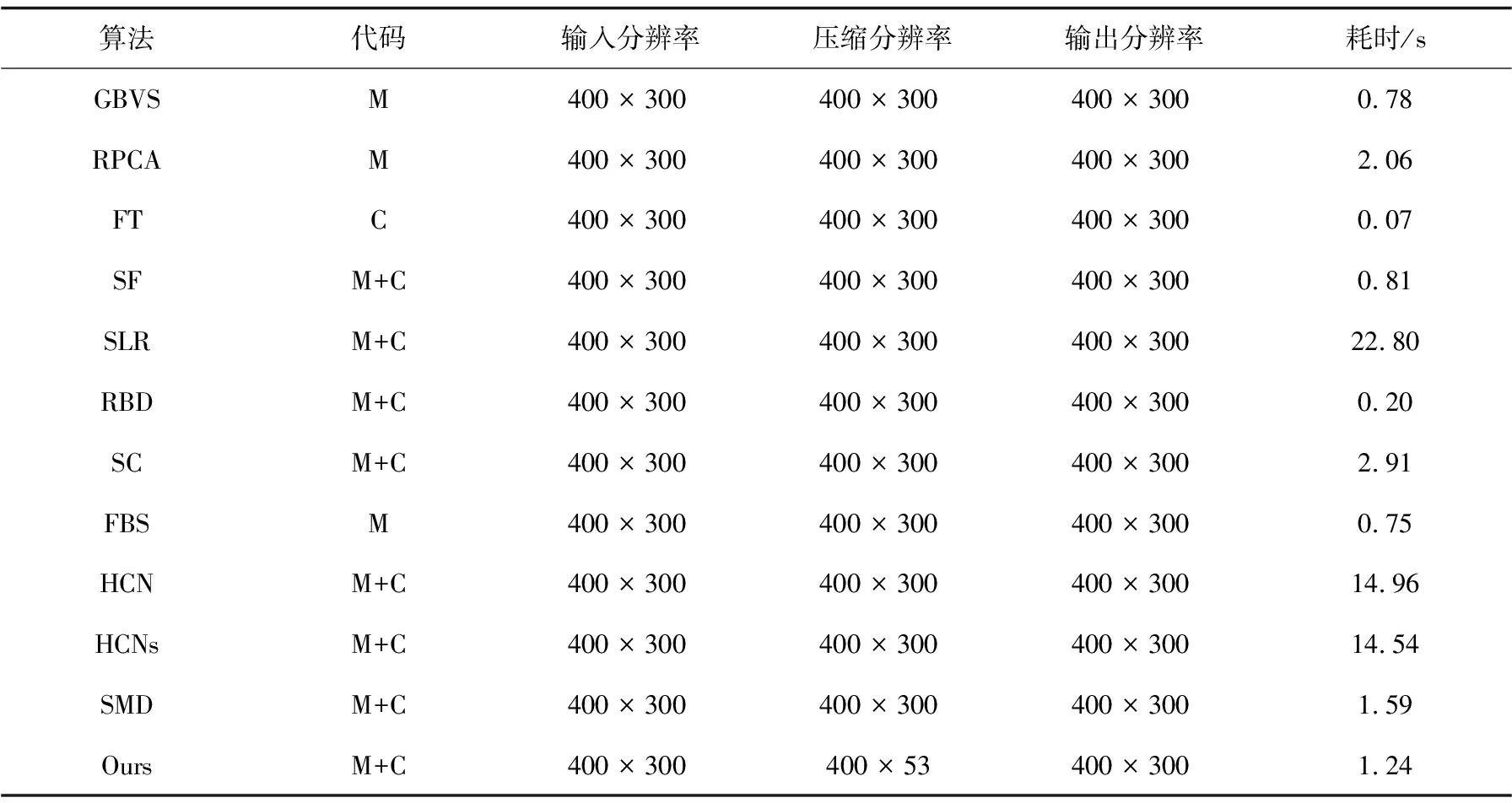
(1)在通常情況下選擇兩個正整數r和k(k (2)通過Arnoldi算法得到r步Arnoldi分解: (5)利用Krylov-SVD重啟方法以及收斂和鎖定技術,產生一個長度為k的Arnoldi分解: (6)利用Arnoldi過程將該分解擴展為一個長度為r的Arnoldi分解: 然后轉步驟(2)。 在本節中,采用了三個數據集十一種算法進行了廣泛的實驗以驗證算法的有效性。三個數據集為:MSRA10K數據集中包含10 000幅圖像,每幅圖像中有一個顯著對象;SOD數據集中包含300幅圖像,每幅圖像中背景復雜且有多個顯著對象;ECSSD包含1 000個背景混亂的圖像。十一種結合先驗信息的顯著性檢測算法為GVBS[18]、FT[19]、RPCA[20]、SF[14]、SLR[8]、RBD[21]、SMD[10]、HCN[22]、HCNs[23]、SC[24]、FBS[25],其中RPCA、SLR、SMD是基于低秩恢復的顯著性算法。文中實驗是在Win10,64位操作系統,Intel(R) Core(TM)i7-8750H CPU 2.2 GHz,RAM 16 GB環境下運行。 實際應用中,算法的穩定性和耗時都是值得關注的問題,但是在以往研究中關于這方面的工作較少。因此,文中將使用1 000幅顯著圖像來分析算法的穩定性和耗時,將算法的耗時定義為:從輸入圖像到輸出顯著圖所需要的時間。對1 000張圖像運行1次取耗時平均值,結果如表1所示。由表1可以看出:在W×H的顯著圖像上,文中算法耗時低于SMD算法能達到1.24幀/秒,且在計算過程中圖像像素可壓縮至W×53,所以文中算法可滿足實時性要求。 表1 視覺顯著性模型的耗時 為了進一步評估算法的優越性,本節將采用PR曲線、AUC值、F-measure值以及平均絕對誤差(MAE)[6]這四種評價指標和現有的十一種算法:GVBS、RPCA、 FT、SF、SLR、RBD、SC、SMD、HCN、HCNs、FBS作對比以進行系統地比較,在MSRA10K數據集、SOD數據集和ECSSD數據集上進行定性、定量測試。圖2為三個數據集的ROC曲線,圖3提供了顯著圖的定性比較。此外,表2列出了在AUC、F-measure和MAE評估指標上的評估結果。結合圖表可以看出,在大多數情況下,算法在三個數據集上表現優異。 圖2 ROC曲線 圖3 不同顯著性檢測方法分別在MSRA10K、SOD、ECSSD數據集上的顯著目標圖 表2 不同顯著性檢測方法在三個數據集上的指標得分 續表2 在表2中提供的算法與其他算法的定量比較,從圖2和圖3的定性比較中可以看到,RPCA算法和SLR算法利用拉格朗日方法生成的低秩矩陣無法生成統一的檢測結果。SMD算法優于以上兩種算法,然而SMD算法使用拉普拉斯正則化生成的低秩矩陣無法得到邊界清晰的顯著目標圖,相比之下,文中使用結構化低秩矩陣Krylov-SVD分解,更加注重圖像中的空間結構,容易得到完整的顯著目標。從表2的定量比較可以看出,文中的低秩恢復算法都大大優于SMD算法、RPCA算法和SLR算法。值得注意的是,在MSRA10K和SOD數據集上,文中顯著性算法略優于其他顯著性算法。而在ECSSD數據集上,就所有三個指標而言,文中的低秩恢復算法甚至優于層級融合的HCNs算法和HCN算法。結合圖表信息可以得出兩個結論:首先,結構化低秩矩陣Krylov-SVD分解算法在背景復雜的圖像中表現優異。其次,Krylov-SVD分解可快速求解低秩矩陣。 結合低秩矩陣Krylov-SVD分解和索引樹結構化,提出了一種基于結構化Krylov-SVD分解的低秩矩陣恢復算法,并將其應用于顯著性目標檢測。該算法通過Krylov-SVD分解求解圖像低秩矩陣和索引樹增加低秩矩陣的空間結構,得到最終顯著圖。將文中算法與現有的十一種算法,在MASK10K、SOD、ECSSD三個公開數據集上進行測試,結果表明文中算法運算快速簡潔,而且可獲得顯著目標完整、結構緊湊的顯著性分割結果。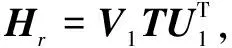
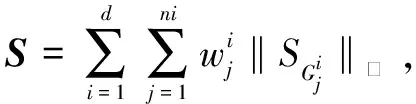
3 實驗結果及分析
3.1 算法的穩定性和運行時間對比
3.2 顯著性算法對比實驗





4 結束語

