基于雙目圖像融合的孔軸配合間隙監視

徐智涵，袁道成，李璐璐

(中國工程物理研究院 機械制造工藝研究所，四川 綿陽 621000)

0 引 言

隨著現代制造業的快速發展，裝配成功率過低的問題越來越突出。由于人工裝配效率較低，所占的生產面積較大，并且裝配質量容易受到操作人員主觀因素的影響[1]，因此實現裝配自動化是提高裝配效率、提升產品質量的重要手段。為了提高自動化裝配質量，需要提高裝配系統的裝配精度。一般而言，提升裝配精度的關鍵在于保證裝配件與裝配基礎件之間的相對位姿精度，并精確控制裝配件與裝配基礎件之間的裝配間隙[2]。裝配精度直接影響了裝配任務的難易程度和裝配效率，因此在產品的裝配作業中起著舉足輕重的作用。此外，在裝配過程中，還需要要求裝配件在裝配路徑上不發生運動碰撞，以造成裝配件與裝配基礎件的表面劃傷和工件變形，因此對裝配系統的裝配精度提出了進一步的要求。

然而隨著裝配間隙的不斷縮小，受到機器人定位精度的限制，系統的裝配精度無法滿足實際裝配需求。因此需要改進裝配策略，提高裝配系統的定位精度，并實現對孔軸裝配質量的實時監視。隨著計算機技術與光電技術的快速發展，視覺傳感器在自動裝配中得到了廣泛的應用。基于視覺伺服的控制策略以視覺傳感器的輸出作為反饋信號，可以對裝配環境進行實時動態的監視，并有效提升零部件的對準效率[3]。Kim等提出了一種基于虛擬視覺的零件對準與形變測量系統，該系統可以實時獲得多視角下的孔軸圖像，實現對工件相對偏移量的測量，并可以有效測量軸件的形變量[4]。視覺傳感器的引入顯著提高了裝配系統的效率與靈活性。

然而，由于相機標定誤差，圖像噪聲以及目標邊緣提取誤差的存在，基于視覺伺服的裝配系統的定位精度受到了限制。因此在自動化裝配中，視覺伺服通常與其他裝配策略相結合。Huang等結合視覺引導與PID控制，使用Baxter機器人成功實現了間隙為1 mm的裝配任務[5]。Lin等設計了一種基于孔軸位姿測量的自動裝配系統，在視覺伺服的基礎上引入了DMP控制策略，顯著提高了孔軸配合的成功率[6]。Zheng等提出了一種結合視覺/力引導與雙臂協調的裝配策略，實驗表明，當裝配間隙在0.5 mm時，工件的配合成功率可達90%以上[7]。Song等提出了一種面向復雜形狀工件裝配的裝配控制策略，結合目標工件的CCD模型，可以從圖像中獲得工件的幾何參數和相對位姿，結合阻抗控制就可以成功引導孔軸配合[8]。Lanzetta等提出了一種基于視覺與力覺混合控制的裝配策略，視覺反饋提供的孔軸相對位姿的估計值可以為六軸F/T傳感器提供初始位姿信息[9]。

當裝配間隙的尺度小于機械臂的定位精度時，裝配系統難以實現精確的裝配。裝配間隙反映了裝配零部件間的相對位置關系，進而反映了裝配過程的質量。因此為了提升裝配質量和效率，需要在裝配過程中實時動態地監視裝配間隙的變化。此外，對于高精密的工業產品，還需避免裝配過程中零部件間的相互接觸，以防止劃傷產品表面或引發工件形變，因此基于力控制的裝配策略難以適用于這類裝配場合。為了提升裝配間隙的測量精度，降低后續圖像處理難度，要求圖像上間隙的尺寸足夠大。然而，現有的測量系統一般通過縮短物距的方式增大配合間隙在圖像上的尺寸，然而這會帶來嚴重的視場受限與遮擋問題，導致測量系統難以在裝配過程中獲得完整的配合間隙信息。

為了解決孔軸配合監視中的視場遮擋問題，消除視場盲區，并對小配合間隙進行實時監視，該文提出一種基于雙目圖像融合的孔軸配合間隙監視技術。通過圖像中的圓孔邊緣信息可以計算圓孔所在的支撐平面與像面之間的單應變換關系，從而可以將雙視角下拍攝的圖像同時重映射至同一個測量平面上，以便進行雙目圖像融合。融合后的圖像包含了兩個視角下的圖像信息，因此可以有效解決視場受限與遮擋問題。由于二次曲線的切點-切線關系經過平面單應變換后仍能保持不變，該文基于Nelder-Mead單純形搜索法計算軸件與圓孔支撐平面間的虛擬交線的幾何參數。確定幾何參數后，虛擬交線與圓孔輪廓共同反映了完整的孔軸配合間隙信息。

1 平面單應變換下二次曲線的相切不變性

不變量作為計算機視覺中的重要研究領域，是對物體三維結構的本質描述與高度概括[10]。圖像中的不變量不會隨著成像條件，如相機內參、相機視角、環境光照等因素的變化而變化，在不同圖像中仍保持不變，具有高度的可靠性和穩定性[11-13]。由群論的定義可知，不變量指的是圖像在某種變換群下保持不變的性質。計算機視覺中的不變量可以按照不同的分類方式進行分類：根據變換群的類別不同，可以將不變量分為射影不變量、仿射不變量、相似不變量等；根據不同的數學構造方式，可以將不變量分為代數不變量、幾何不變量、微分不變量與積分不變量等[14]。通過構造并提取二維圖像中的不變量，可以為計算機視覺應用提供穩定的信息來源，實現相機參數的自標定[15-16]、恢復目標物體的三維結構[17]、實現目標或動作識別[18-19]等任務。

相切關系作為二維圖像中常見的幾何關系，可以為求解平面曲線方程、目標識別與定位提供輔助信息。為了求解圖像中的待求二次曲線，通過在圖像上提取該二次曲線的切點或切線方程，可以輔助求解二次曲線方程，進而獲得該二次曲線的幾何參數。由于圖像中二次曲線的相切關系在平面單應變換下是一個不變量，即二次曲線的切點切線經過平面單應變換后仍能與投影二次曲線保持相切關系，因此可以將像面上的源圖像重映射至易于觀察和處理的其他平面，從而降低二次曲線幾何參數的求解難度。平面單應變換下的二次曲線相切不變性表述如下：

(1)

可以得到，平面Π0上的二次曲線、切線、切點經過平面單應變換后仍滿足以下關系[20]：

(2)

(3)

(4)

公式(2)表明，二次曲線C0上一點p0，經過單應變換后，投影點p1仍在投影二次曲線C1上；公式(3)表明，若直線l0為二次曲線C0的一條切線，則經過單應變換后，投影直線l1仍為投影二次曲線C1的切線；公式(4)表明，若點p0為切線l0關于二次曲線C0的切點，則經過單應變換后，投影點p1為投影切線l1關于投影二次曲線C1的切點。

綜上所述，二次曲線的切點切線在平面單應變換下保持不變，即平面上二次曲線的一對切線切點，經過平面單應變換H后，在像平面上的投影直線與投影點仍是關于投影二次曲線的一對切線切點。因此可以通過平面單應變換將某平面上的二次曲線與切線切點同時變換至另一個平面上，降低平面曲線幾何參數的求解難度，并方便后續的觀察和處理。

2 基于雙目圖像融合的孔軸間虛擬交線提取

2.1 平面單應矩陣計算

為了實現圖像融合，首先需要將不同視角下拍攝的圖像重映射至同一測量平面。在進行圖像重映射之前，需要獲得相機內部參數，以及像面與測量平面之間的單應變換關系H。相機的內部參數可以通過準確的相機標定得到。為了計算像面與測量平面之間的單應變換關系H，該文將圓孔所在支撐平面作為測量平面，坐標系建立方式如下：

以支撐平面上圓孔的幾何中心為世界坐標系的原點Ow，支撐平面為世界坐標系Zw=0平面建立世界坐標系，如圖1所示。以左相機坐標系1為例，世界坐標系相對于相機坐標系之間的剛體變換關系為(R,t)，其中R為旋轉矩陣，R=[r1,r2,r3]，t為平移向量。在上述坐標系建立方式下，相機坐標系下圓孔所在支撐平面的法向量與圓心位置為(r3,t)。

圖1 世界坐標系與相機坐標系

像平面上的一點(u,v)T與世界坐標系下Zw=0平面上的一點(Xw,Yw)T之間的射影變換關系為:

(5)

其中，λ為非零常數；Kc為相機的內參矩陣；ri,i=1,2,3為旋轉矩陣R的第i列向量。通過計算相機坐標系下圓孔的相對位姿(r3,t)，可以獲得圓孔支撐平面與像平面之間的單應變換關系H=Kc[r1,r2,t]。根據圓的投影方程，像面上投影橢圓的對偶C*滿足[21]：

(6)

其中，k為非零常數；r為圓半徑；對方程等式右邊進行奇異值分解，可以反求圓孔的相對位姿(r3,t)。具體的計算方法在文獻中已經得到詳細的闡述[22]，在此不再贅述。

在根據圓的投影方程求解的圓孔空間位姿參數(r3,t)中，r3的可能解有兩個。通過雙視角下測量的圓位姿參數在同一個測量坐標系下的一致性[21]，可以消除計算結果中的冗余解。在實際測量中，由于圖像噪聲、標定誤差的存在，左右相機的測量結果在同一個測量坐標系下不可能完全一致。因此通常設置一個閾值ε，當不同視角下測量的法向量在同一測量坐標系下的夾角大于閾值ε時，對應的法向量為冗余解。

在獲得圓孔所在平面法向量r3=(r31,r32,r33)T與圓心位置t的唯一表示后，根據右手定則，支撐平面上的向量r1,r2的一組可能解可以通過如下方式計算得到：

(7)

2.2 圖像重映射與雙目圖像融合

圖像重映射是指將源圖像按照指定的映射函數進行映射，從而形成新的目標圖像的過程[23]。通過選擇合適的映射關系，圖像重映射可以將源圖像映射至其他平面。相比于源圖像，生成的目標圖像易于觀察和處理。圖像重映射還可以將多個視角下拍攝的圖像映射至同一測量平面，以便進行后續的圖像融合。假設源圖像與目標圖像之間的映射關系為：

g(uw,vw)=f(h(uw,vw))

(8)

其中，g(·)表示目標圖像，f(·)表示源圖像，h(uw,vw)表示像素間的映射函數。由公式(5)可知，當源圖像上一點(u,v)T坐標已知時，世界坐標系Zw=0平面上的對應點(Xw,Yw)T可以通過公式(9)計算得到：

(9)

在獲得源圖像上的一點在世界坐標系Zw=0平面上的對應點坐標后，此時坐標單位仍屬于物理長度單位，還需要經過進一步采樣轉換為圖像像素單位：

(10)

其中，s為采樣常數，表示目標圖像上單像素代表的實際物理長度；u0,v0表示世界坐標系的原點在目標圖像上的像素位置。在計算過程中出現非整數坐標的像素值可以利用雙線性插值法計算得到。在獲得映射圖像g1,2后，對映射圖像加權平均，得到最終的雙目融合圖像。

左右視角下的源圖像、映射圖像與最終的融合圖像如圖2所示。如圖2(c)所示，在雙目融合圖像中，雙視角下拍攝的圓孔輪廓完全重合。融合圖像中兩個圓柱圖像區域互相交疊，因此在雙目融合圖像中可以觀察到兩個圓柱共四條邊緣直線。

圖2 雙目圖像融合過程

2.3 孔軸間虛擬交線幾何參數優化

孔軸間虛擬交線指的是孔軸配合過程中軸件與圓孔所在支撐平面間的虛擬交線，該虛擬交線在圖像上不可見，虛擬交線與圓孔輪廓可以共同反映圓孔支撐平面上的孔軸配合間隙。孔軸配合過程如圖3(a)所示，其中，E1為圓孔的邊緣輪廓，E2為圓柱與圓孔支撐平面Π之間的虛擬交線。由空間幾何關系可知，虛擬交線在像面上的投影一定與圓柱的兩條投影邊緣相切。

圖3 孔軸配合過程與雙目融合圖像上的虛擬交線的幾何參數

由第一節可知，二次曲線的切線切點經過平面單應變換后在像面上仍保持相切關系。因此在利用平面單應變換進行圖像重映射和雙目融合后，雙目融合圖像中兩個圓柱的四條邊緣投影直線li,i=1,2,3,4仍與虛擬交線相切。如圖3(b)所示，在雙目融合圖像中，圓孔邊緣為e1，半徑為b1，虛擬交線為橢圓e2，橢圓e2的半長軸、半短軸分別為a2,b2，中心坐標為(u2,v2)，偏轉角為θ2。由空間幾何關系可知，虛擬交線E2的半短軸與圓柱半徑R2相等，因此在雙目融合圖像上虛擬交線的半短軸b2滿足線性關系R1/R2=b1/b2，其中R1為圓孔邊緣E1的半徑。

當確定虛擬交線半短軸長度b2后，虛擬交線方程的剩余自由度為4。為了求解虛擬交線e2的其余幾何參數(u2,v2,a2,θ2)，根據雙目融合圖像中存在的相切關系，將參數求解問題轉換為最小化目標函數:

(11)

該最小化問題為一個無約束的多參數優化問題，該文基于Nelder-Mead單純形搜索法對該問題進行迭代求解。Nelder-Mead單純形搜索法是一種用于優化無約束多參數問題的搜索算法，其基本原理為在n維參數空間中用初始值隨機構建包含n+1個節點的凸多面體，即單純形，通過各節點目標函數值的比較排序來決定對多面體各節點采取反射、擴張、收縮與壓縮操作，最終通過不斷迭代優化使得該單純形逼近最優解[24-25]。Nelder-Mead單純形搜索法具有搜索速度快，無需求解目標函數梯度值，對初始值的選擇不敏感等優點。當Nelder-Mead算法陷入局部最優時，僅需重啟優化算法即可[26-27]。優化算法框圖如圖4所示。

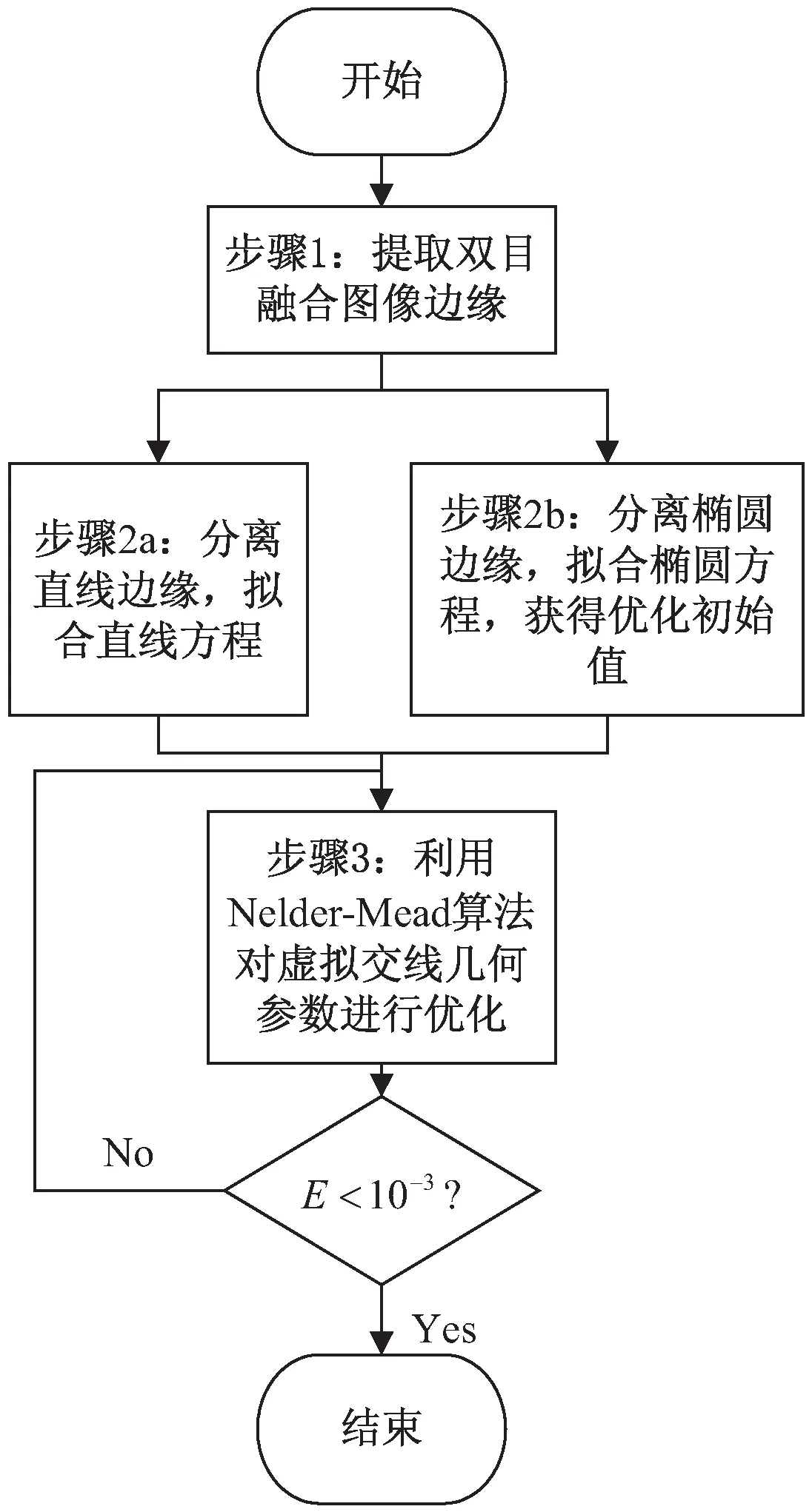
圖4 虛擬交線幾何參數優化流程

3 實驗驗證

該文首先通過計算機仿真方法驗證基于雙目圖像融合的孔軸間虛擬交線提取算法的可行性。首先在計算機中生成虛擬的雙目立體視覺系統，系統結構為：左右相機的光軸互相平行，其中世界坐標系與左相機坐標系重合，右相機坐標系的原點在世界坐標系中的坐標為(0.01,0,0)，兩相機內部參數相同，內參矩陣為:

同時在世界坐標系中生成圓柱與圓孔的三維模型，其中圓孔的半徑R1=1.75 mm，圓柱的半徑R2=1.5 mm。仿真實驗研究當孔軸軸線間有一小角度夾角，且孔軸相對位置發生偏移時，虛擬交線幾何參數的求解結果。圓孔相對于世界坐標系的旋轉矩陣與平移向量為：

圓柱軸線相對于世界坐標系OwZw坐標軸的旋轉矩陣為：

生成孔軸三維模型后，將三維模型投影到指定內參與位姿的相機像平面上。左右相機拍攝的源圖像與最終的雙目融合圖像如圖5所示。

圖5 雙目融合示意圖

圖5(a)～圖5(c)中，長短軸較短的橢圓代表孔軸間虛擬交線在像面上的投影橢圓，而長短軸較長的橢圓代表圓孔邊緣在像面上的投影橢圓。在圖5(c)雙目融合圖像中存在四條直線邊緣，分別為左右圖像中兩個圓柱區域圖像經過映射融合形成的。從圖像中可以看出，虛擬交線均與圓柱邊緣滿足相切關系。對雙目融合圖像進行亞像素邊緣提取，并分離得到的圓邊緣和直線邊緣。在對直線邊緣和圓邊緣進行進一步的非線性擬合后，可以得到四條邊緣直線與圓孔邊緣在圖像上的方程。輸入Nelder-Mead優化算法對圓柱與圓孔支撐平面的虛擬交線幾何參數進行迭代優化。圖6為仿真實驗中虛擬交線的最終優化結果。

圖6 虛擬交線優化結果

在設置的實驗參數下，對應的圓柱與圓孔支撐平面的虛擬交線幾何參數理論值與迭代計算結果如表1所示。

表1 虛擬交線幾何參數實驗結果對比

仿真實驗結果表明，該文提出的算法可以很好地收斂到最優值，幾何參數的計算結果與理論值接近。虛擬交線與圓孔輪廓共同反映了孔軸配合間隙信息。為了進一步驗證算法可行性，對真實環境下孔軸配合虛擬交線的幾何參數進行求解。參與配合的軸件半徑R2=1.5 mm，圓孔半徑R1=1.75 mm，最大配合間隙為0.5 mm。圖7(a)～圖7(c)分別為左右相機下的源圖像、世界坐標系Zw=0平面上的映射圖像以及經雙目融合得到的圖像。孔軸間虛擬交線提取算法結果如圖8所示。從圖像中可以看出，幾何參數經由Nelder-Mead算法迭代優化后，虛擬交線與雙目融合圖像中軸件的四條邊緣基本滿足相切關系，算法可以收斂至最優值。

圖7 圖像重映射與融合圖像

圖8 優化算法提取的孔軸虛擬交線

在真實環境下的孔軸配合虛擬交線提取實驗中，由于相機內外參數標定誤差的存在，在圖像重映射過程中，算法難以將不同視角下拍攝的圖像完全映射至世界坐標系的同一個測量平面上；此外由于亞像素邊緣提取算法精度限制以及圖像噪聲的存在，與仿真實驗的結果相比，優化后的孔軸間虛擬交線的幾何參數與理論值相比有所偏差。

4 結束語

該文提出了一種基于雙目圖像融合的孔軸配合間隙監視技術。算法通過圖像中的圓孔輪廓計算圓孔支撐平面與相機像平面之間的單應變換關系，從而將雙相機獲得的圖像重映射至圓孔支撐平面上，并進行雙目圖像融合。由于二次曲線的切點切線關系經過平面單應變換后仍能保持相切關系，在雙目融合圖像中使用Nelder-Mead算法對孔軸間虛擬交線的幾何參數進行迭代優化。實驗結果表明，提出的方法可以有效收斂，優化后的虛擬交線幾何參數與理論值接近，虛擬交線與圓孔輪廓可以共同反映圓孔支撐平面上的孔軸配合間隙信息，可以對裝配間隙0.5 mm以下的孔軸配合進行監視。