統計工具在高性能玻璃纖維產品質量控制中的應用

張啟勇，張 梅，朱 斌，祖 群，于 水，郭仁賢

（南京玻璃纖維研究設計院有限公司，南京 210012）

0 前言

玻璃纖維是一種典型的無機非金屬材料，具有質量輕、強度高、耐高低溫、耐腐蝕、隔熱、阻燃、吸音、電絕緣等優異性能以及一定程度的功能可設計性，是一種優良的功能材料和結構材料。高性能玻璃纖維是指與傳統玻璃纖維相比，某些使用性能有顯著提高，能夠在外部力、熱、光、電等物理以及酸、堿、鹽等化學作用下具有更好的承受力。高性能玻璃纖維種類多，纖維制品規格也很多，主要有無捻粗紗、有捻紗、織物3大類，其中紗線類產品根據玻璃類別、線密度、浸潤劑類別、捻度、捻向、卷裝量等可細分出近千個規格制品。如此大量的產品規格，必然產生龐大的性能測試數據。

隨著市場需求的不斷提升、生產規模不斷擴大，客戶對產品的質量要求也越來越嚴格。

質量管理經歷了4個發展階段：由初級階段發展到質量檢驗階段，接著發展到統計質量控制階段，再進而發展到全面質量管理階段，這一系列的跨越離不開統計工具的應用。在各種統計工具的應用中，常用的統計工具、方法有很多。統計分析工具的應用可以幫助公司了解數據的變異，從而有助于組織解決問題并提高有效性和效率，這些工具也有助于更好地利用可獲得的數據進行決策，有助于對變異進行測量、描述、分析、解釋和建立模型，甚至在數據相對有限的情況下也可實現。同時有助于解決，甚至防止由變異引起的問題，并促進持續改進。也可以規范生產過程中數據分析的方法，為質量分析方法的選擇提供指導，熟練運用相應的圖表，從而提高工作效率［1，2］。

針對高性能玻璃纖維的質量控制要求，本文以先進復合材料用高性能玻璃纖維產品為例，借助統計分析軟件，采用檢查表、柏拉圖、控制圖、正態分布、直方圖、不合格品數控制圖等方法，通過數據的收集與分析，指導相關技術人員開展工作，并針對不同的數據類型，采用相對應的統計工具和分析方法，從而進一步提高產品的質量穩定性。

1 統計技術用工具的基本原理

在一個統計問題中，稱研究對象的全體為總體，構成總體的每個成員稱為個體，若關心的是研究對象的某個數量指標，那么將每個個體具有的數量指標X稱為個體，這樣一來，總體就是某數量指標值X的全體（即一堆數），這一堆數有一個分布，從而可用一個分布描述，簡單地說，總體就是一個分布。統計學的主要任務就是：研究總體是什么分布，這個總體分布的均值、方差（標準差）是什么？從總體中抽取部分個體所組成的集合稱為樣本。樣本中的個體在強調其具體實物時也稱為樣品，樣本中所包含的個體的個數稱為樣本量。常用n表示從總體中抽取樣本是為了認識總體，即從樣本推斷總體，分布，總體均值，總體標準差。對結果有效，對樣本的抽樣要求。抽樣切記受到干擾，特別是人為干擾，某些人為的傾向性會使所得樣本不是簡單隨機樣本，從而使最后的統計推斷失效［3，4］。

1.1 檢查表

檢查表是按照系統工程方法，在對一個系統進行科學分析的基礎上，找出各種可能存在的風險因素，然后以提問的方式將這些風險因素列成的表格。可按團隊、設備、時期等類別，由風險管理專業人員、生產技術人員和現場工人共同參與編制［5］。

1.2 控制圖

控制圖是對過程質量特性進行測定、記錄、評估，從而監控過程是否處于控制狀態的一種統計方法的圖，由3條平行的直線組成，包括中心線、上控制線、下控制線，并有按時間順序抽取的樣本統計量數值的描點序列。常規控制圖的原理是基于“小概率事件不容易發生，一旦發生說明有異常情況”。如果小概率事件發生了，說明制造過程發生了異常波動。表1是常規控制圖的控制限公式。

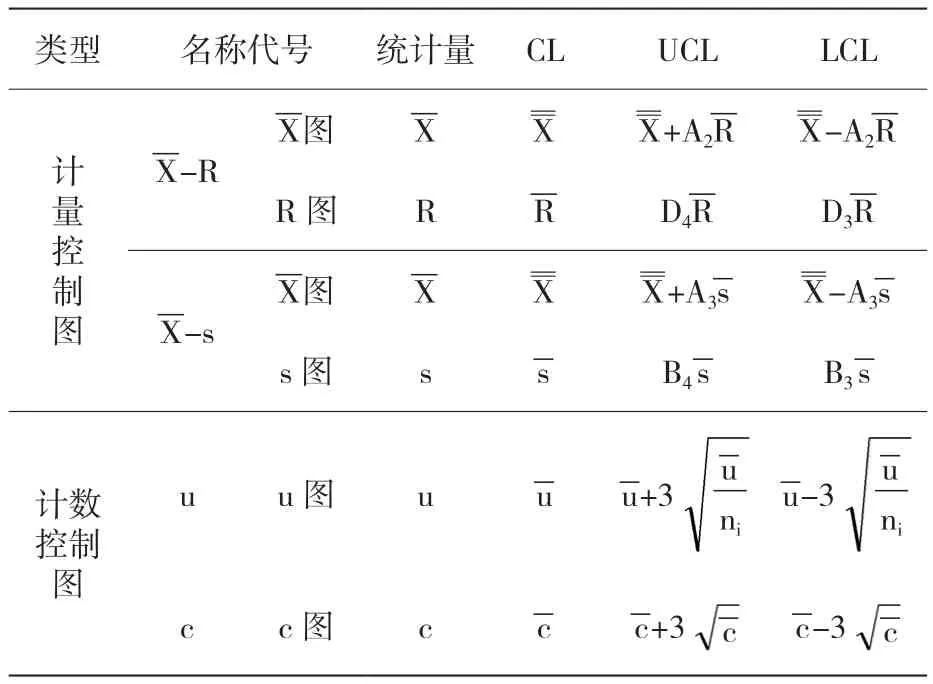
表1 常規控制圖控制限公式

表中：A2、A3、B3、B4、D3、D4——系數，查表可知。

1.3 正態分布N（μ、σ2）

質量管理中最重要也是最常用的分布，它能描述很多質量特性X隨機取值的統計規律性。正態分布含有兩個參數μ、σ，常記N（μ、σ2）。其中μ為正態分布的均值，位置參數，正態分布的中心，質量特性X在μ附近取值的機會最大；σ2是正態分布的離散程度，σ＞0是正態分布的標準差，σ越大，數據分布越分散；σ越小，數據分布越集中［6］。

1.4 柏拉圖

柏拉圖又稱為排列圖，帕累托圖，主次因素分析法、柏拉托圖法等，它是根據“關鍵的少數和次要的多數”的原理而制做的。也就是將影響產品質量的眾多影響因素按其對質量影響程度的大小，用直方圖形順序排列，從而找出主要因素。柏拉圖的結構為兩個縱坐標和一個橫坐標，由數個直方形和一條折線構成。左側縱坐標表示頻率，右側縱坐標則表示累計頻率（以百分比表示），橫坐標表示影響質量的各種因素之名稱，按影響大小順序排列，直方形高度表示相應的因素的影響程度（即出現頻率為多少），上方折線則表示累計頻率線（又稱帕累托圖曲線）。通常累計百分比將影響因素分為三大類：占0～80%為A類因素，也就是主要因素；80%～90%為B類因素，是次要因素；90%～100%為C類因素，即一般因素［7］。

1.5 直方圖

直方圖又稱質量分布圖，是一種統計報告圖，由一系列高度不等的縱向條紋或線段表示數據分布的情況。一般用橫軸表示數據類型，縱軸表示分布情況。這是一個連續變量（定量變量）的概率分布的估計，它是一種條形圖。為了構建直方圖，第一步是將值的范圍分段，即將整個值的范圍分成一系列間隔，然后計算每個間隔中有多少值。這些值通常被指定為連續的，不重疊的變量間隔。間隔必須相鄰，并且通常是（但不是必須的）相等的大小。它是表示資料變化情況的一種主要工具［8，9］。用直方圖可以解析出資料的規則性，比較直觀地看出產品質量特性的分布狀態，對于資料分布狀況一目了然，便于判斷其總體質量分布情況。

1.6 分析軟件

采用美國SAS軟件公司的JMP統計分析軟件，JMP的算法強調統計方法的實際應用，交互性、可視化能力強，使用方便，適合非統計專業背景的數據分析人員使用。

2 數據收集及數據庫建立和分析

2.1 檢查表實例分析

統計方法進行質量控制主要依據是數據，數據要反映客觀的實際情況，不應有虛假的成分，否則即使進行了嚴格的、精確的計算和分析，其結果仍不可信，調查表就是一種很好的收集數據的方法。根據現有標準文件中規定的要求，收集了織物外觀檢驗的數據，將需要統計的關鍵特性錄入Word中，制定成統一的格式，受控下發。

通過圖1可以看到布卷外觀檢驗記錄表的情況，對工序質量或產品質量進行檢查與確認。尤其是織物外觀的檢查項目多，易遺漏，圖1的檢查表可以逐項進行，避免了錯誤和重復性的檢查。使操作人員能夠嚴格遵守操作規程的要求，保證產品質量，在批量很大的工作中，可以收集有意義、有價值的數據，為后續開展質量分析、質量控制提供了織物外觀的數據積累和支撐。

圖1 外觀檢驗記錄表

2.2 控制圖

2.2.1 計量控制圖實例分析

選用一個典型性的產品，并選取其生產過程產品線密度進行數理統計分析。將數據輸入Excel表中，再將上述Excel數據導入統計分析軟件，如表2所示，報表的行列設計應兼顧JMP軟件中數據表中計算取值規則。通過統計軟件操作，可以獲得線密度均值和移動極差控制圖，見圖2。

圖2 線密度控制圖

表2 線密度數據表

2.2.2 計數控制圖實例分析

選用一個典型性的織物產品，選取其生產的過程產品外觀疵點進行數理統計分析。將數據輸入Excel表中，再將上述Excel數據導入統計分析軟件，如表3所示，報表的行列設計應兼顧JMP軟件中數據表中計算取值規則。通過統計軟件操作，可以獲得外觀疵點控制圖，見圖3。

圖3 外觀疵點控制圖

表3 外觀疵點數據表

以下判定準則為GB/T 4091-2001《常規控制圖規定》的判定準則，可優先選用的判定準則。也可以按其他方式確定判定規則，但必須在作業指導書或工藝文件得到規定，并經過批準方可使用。一旦發生異常波動，就應該盡快找出原因，采取措施加以消除。

通過以上匯總的結果，可以看到有捻紗的線密度、織物疵點數的測試結果都在控制限內，過程穩定。如果控制圖出現異常，表明需采取糾正措施，根據異常判定原則［5］，異常產生后的措施包括：

（1）對過程進行驗證，如條件允許，可停工進行驗證。

（2）提高檢測頻率，并對異因進行分析調控，直至過程受控。

（3）將最后時段生產的產品進行隔離，加大抽檢量，如有可能對其進行全檢，找出不合格品。

（4）將所有不合格品進行隔離并進行標識。

（5）不合格品返工、返修或報廢。

（6）如原因不在本工段，通知責任區域/部門。

2.3 數據分布實例分析

跟蹤240 tex無捻粗紗在線監測線密度數據，對數據進行匯總分析，通過統計軟件的操作，形成線密度正態分位數圖，見圖4、圖5。可以看出，無捻粗紗線密度整體呈正態分布，均值為239.59 tex，散度σ為3.65，散度較小，說明集中度較好，以239.59 tex為中心值，線密度在230~250 tex階段的粗紗概率為100%。根據標準要求，240 tex無捻粗紗公稱線密度為240 tex，合格范圍為222~258 tex，這表明生產的粗紗線密度質量穩定可靠。

圖4 無捻粗紗線密度概率密度分布

如果對產品的線密度按批次進行正態分位數圖做進一步分析，對比該產品線密度均值和散度σ歷史水平，可以知道現行生產的批次產品線密度的分布情況，如有較大偏離，應及時進行原絲或紗團配比組合，起到提前預警作用。如圖5所示，當線密度在238~239 tex之間出現“缺口”（該段出現概率偏低）時，應考慮增加部分該段內的線密度粗紗，使產品分布更加合理，最終滿足客戶對線密度更窄控制范圍要求。由此可見，數據的分析結果，可科學、有效地實施批產品性能參數合理分布及質量可控的目的，同時提高了工作效率。

圖5 批次內無捻粗紗線密度統計圖

2.4 柏拉圖實例分析

選定了需要分析的項目，對問題的現象、狀況、原因加以層別分類；根據檢查表收集的內容，把發生的織物疵點分別錄入，匯總分析整理數據，見表4，通過統計軟件的操作，形成分類項目匯總表，分類項目按數據多少由大到小排列，見圖6。

表4 外觀疵點數據

圖6 外觀疵點匯總圖

通過以上匯總的數據可以看到，該產品外觀的疵點匯總結果，從圖中可以看到主要疵點是“經緯紗污染”等，應有針對性的采取措施。其核心就是帕雷托法則又稱80/20法則。學會了它，能讓你在工作中不必花大部分時間浪費在無用的問題上，用更少的精力解決更大的問題，用更少的付出收獲最多的收益。

2.5 直方圖實例分析

跟蹤240 tex無捻粗紗在線監測線密度數據，從穩定正常的生產過程中得到的數據所做出的直方圖，對數據進行匯總分析，通過統計軟件的操作，形成線密度直方圖。見表5、圖7可以看出，無捻粗紗線密度整體呈正態分布。

表5 線密度統計結果

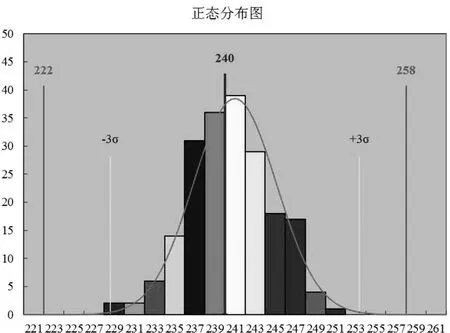
圖7 線密度正態分布圖

參照典型的直方圖的分析［10］：

根據匯總的數據，可以看到該批次產品呈標準分布，整體的平均值于最大值和最小值的中間值相同或接近，平均值附近的數據頻數最多，頻數在中間值向兩邊緩慢下降，以平均值左右對稱，整體狀態穩定，這種形狀也是最常見的。

3 結論

統計工具的應用，是根據不同的問題，采用不同的分析方法，使高性能玻璃纖維產品生產過程質量更加的穩定，通過匯總分析，可以得出以下結論。

（1）對產品檢驗結果的匯總分析，統計工具的使用，可以監控過程的穩定性，發生異常情況時及時預警，同時對人員的培訓有助于產品質量穩定性的提高。

（2）通過檢查表、柏拉圖、直方圖以及正態分布的使用，可以有效利用數據進行統計分析，能夠快速地抓住高性能玻璃纖維生產過程中的主要矛盾，找到問題癥結，及時制定相應的措施從而解決問題，提高了工作效率，對產品質量控制也不是憑直覺或者經驗，而是科學、有效地分析、解決問題。

（3）統計工具的使用，可以將數據變成圖表，通過視覺化的符號展現出來，提升對數據的理解能力。

（4）統計工具的使用，是企業實現科學管理及監督的一種重要手段，更是企業用來指導生產、計劃和執行決策的一種依據，是各企業的一項基礎且重要的工作。