基于WOA優化卷積神經網絡的齒輪箱故障診斷研究

劉 奇，唐紅濤，高晟博，李 冰

(1.武漢理工大學 機電工程學院，湖北 武漢 430070；2.武漢理工大學 數字制造湖北省重點實驗室，湖北 武漢 430070)

齒輪具有傳動比大、體積小、承載能力大等優點，同時作為減速箱的關鍵零件，由于其長期處于惡劣的工況條件下，也是設備最易損壞的部分。此外，齒輪一旦出現不同程度的失效，整個減速箱乃至整臺設備都可能出現故障，這些故障引起的設備重大問題屢見不鮮。

為了維持設備的安全運行，避免造成不必要的停機維修損失，需要對齒輪進行狀態監測和故障診斷，這也成為國內外眾多學者的研究對象。例如，雷亞國等[1]從動力學建模和動態信號處理兩方面分析了行星齒輪箱故障診斷的國內外研究進展，指出當前研究中存在的關鍵問題并討論了解決這些關鍵問題的方法和途徑； Hinton等[2]通過“逐層預訓練”來有效克服深層神經網絡在訓練上的困難，從而掀起了深度學習的浪潮。近年來，越來越多的學者開始嘗試將卷積神經網絡(convolutional neural network，CNN)應用于工業設備的故障診斷中,雖然卷積神經網絡的層數、池化方式、激活函數、分類器等結構參數可依據經驗進行選擇，不需要優化，但是卷積核的個數、大小、學習率等參數并沒有明確的選取規則，顯然隨機選擇容易使神經網絡陷入局部最優。

綜上所述，筆者結合鯨魚算法(whale optimization algorithm)，其具有結構簡單、參數少、搜索能力強且易于實現等特點，提出了WOA-CNN診斷模型，利用WOA對卷積神經網絡參數進行優化，避免模型陷入局部最優解。

1 卷積神經網絡

卷積神經網絡[3]結構一般包括輸入層、卷積層、池化層、全連接層和輸出層5部分，筆者主要研究兩個卷積層和兩個池化層的CNN網絡。

1.1 卷積層

卷積過程是用多個卷積核對輸入圖像進行卷積運算，然后將輸出加上偏置后，通過激活函數進行非線性變換，對于二維圖像信號，卷積定義為：

(1)

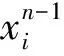
1.2 池化層

池化操作[4]是圖像的下采樣過程，主要作用是對卷積層輸出特征進行壓縮，以減少特征圖。池化方式有最大值池化、均值池化、高斯池化和可訓練池化。針對齒輪周期性振動的時域信號，為了獲取與位置無關的特征，采用最大值池化方式。池化操作運算公式為：

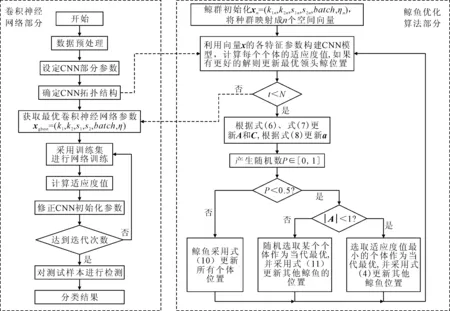
hn=max(jn-1)W

(2)

式中:hn為第n池化層池化結果；jn為第n層第j個池化切片；W為池化區域；fn為第n卷積層卷積結果。

2 基于WOA優化CNN的算法設計

鯨魚優化算法[5](WOA)是一種模擬座頭鯨捕獵的群智能優化算法，其結構簡單、收斂速度快且易于實現。算法分為包圍獵物、泡泡網攻擊和搜索獵物[6]3個步驟，因此，用系數矢量A來區別是環繞包圍獵物還是隨機搜索行為。

為了提高模型的收斂速度和準確率，筆者設計了一種基于WOA優化CNN結構參數的算法(WOA-CNN)，采用WOA對兩個卷積層卷積核的數量k1、k2，大小s1、s2，訓練批次batch，學習率η進行優化[7]，將上述6個參數映射成每頭鯨魚個體的空間向量位置，第n頭鯨魚的位置為：

xn=(k1n,k2n,s1n,s2n,batchn,ηn)

(3)

(1)包圍獵物。鯨群在捕食獵物過程中，對于獵物的位置是未知的，基于動態變換的獵物位置。WOA算法假定目標最佳位置就是鯨魚最接近獵物時的位置，并包圍它。為此，引入系數向量A，當|A|小于1時，選擇鯨魚種群中最接近目標的鯨魚個體作為局部最優獵物xgbest，此時CNN得到的適應度值最小，其余個體向著這個位置逐漸包圍獵物，位置更新公式為：

D=|C·xgbest(t)-xn(t)|

(4)

xn(t+1)=xn(t)-A·D

(5)

式中:t為當前迭代次數；·為逐元素相乘并非向量運算中的點乘；A和C的更新公式為：

A=2a·r1-a

(6)

C=2·r2

(7)

式中:r1、r2是[0,1]中的隨機向量；a為收斂因子，其變化公式可設置為：

(8)

式中:N為最大迭代次數。

(2)泡泡網攻擊。鯨魚在捕食過程中，一方面連續吐出氣泡形成一種圓柱形氣泡網，將獵物包圍起來，采用收縮包圍機制；另一方面會作螺旋姿勢旋轉上升，向水面游動，采用螺旋更新位置機制[8]。假設鯨群選擇收縮包圍和螺旋更新兩種情況的幾率各占50%，則鯨魚位置的更新公式分別為：

xn(t+1)=xgbest(t)-A·

|C·xgbest(t)-xn(t)|p<0.5

(9)

xn(t+1)=D′·ebl·cos(2πl)+

xgbest(t)p≥0.5

(10)

式中:D′=|xgbest(t)-xn(t)|表示第n頭鯨魚到最佳位置的距離；b為螺旋線常數；l為[-1,1]中的隨機數。

(3)搜索獵物。鯨魚可以根據彼此的位置進行隨機搜索，當|A|≥1時，在鯨群中隨機選擇一頭鯨魚xrand(t)作為局部最優位置，并以此更新其他鯨魚的位置。更換公式為：

xn(t+1)=xrand(t)-A·|C·xrand(t)-xn(t)|

(11)

在WOA算法中，每頭鯨魚要朝著獵物的位置移動，鯨群之間更新獵物信息，獵物最終的位置也就是鯨群中位置最優的個體，此時將獵物的位置作為CNN網絡結構的全局最優參數，對應最佳適應度值。WOA-CNN算法流程如圖1所示。 鯨群捕食行為具體步驟為：

圖1 WOA-CNN算法流程圖

(1)信號預處理。由于上述6個物理量有不同的單位和量級，在訓練神經網絡前需要對采集到的數據進行歸一化處理。此外，還需要將一維時域信號轉化成二維“矩陣”，“矩陣”中每一個像素點代表信號值。

(2)數據集劃分。將訓練集、測試集組數按3∶1劃分，并且保證訓練集中各故障類別下的數目相等，用以驗證WOA-CNN模型訓練和測試結果的準確度。

(3)鯨群初始化。鯨群種群初始化參數只有鯨魚種群個數n和迭代次數N，設置n=20，N=70。初始化種群后，種群中的每頭鯨的位置都是用一個6維向量表示適應度評價指標。常用公式包括：平均絕對誤差、均方誤差等，筆者采用交叉熵函數檢驗回歸損失。

(4)捕食行為。捕食行為具體步驟為：

Step1每頭鯨位置更新。當p≥0.5時，鯨群根據式(10)更新個體位置；當p<0.5且|A|<1時，鯨群根據式(4)更新個體位置；當p<0.5且|A|≥1時，鯨群根據式(11)更新個體位置。

Step2計算更新后鯨魚的適應度值。將更新后每頭鯨魚的6維向量作為CNN的結構參數，用訓練集訓練后用測試集測試，計算均方誤差值，記錄每個個體的適應度值和當前迭代時間，并篩選出與當前一代中的最佳適應度值相對應的鯨魚位置。如果更新的局部最優值比上一代的局部最優鯨魚更好，則用xgbest(t+1)取代全局最優鯨魚xbest；反之用全局最優鯨魚xbest取代局部最優鯨魚，并重新更新所有鯨魚的位置，再計算適應度值。

Step3結束條件。判斷迭代次數是否滿足t>N，如果不滿足，則返回Step1重新迭代計算，否則結束局部深度搜索。

(5)故障分類。由于每條鯨魚xi=(k1i,k2i,s1i,s2i,batchi,ηi)的空間位置不同，即每次訓練CNN的結構參數都會發生變化，針對不同的CNN網絡結構參數，用相同的訓練集和測試集來訓練和測試，其中訓練集是已知故障類別標簽的，測試集是標簽未知的。CNN的輸出層采用Softmax函數將輸出信號轉化為概率和為1的分布，計算第i次迭代的平均損失值。最終，鯨群經過N次迭代尋優操作后，找到平均損失值最小的那一代，對應的即為全局最優鯨魚，也就是獵物位置。

(6)模型重構。得到全局最優鯨魚xn=(k1n,k2n,s1n,s2n,batchn,ηn)的位置后，將最優的卷積核數量、大小、訓練批次、學習率等6個參數重構CNN模型，并采用訓練集訓練，測試集測試，此時CNN模型故障分類準確率最高。

3 實驗結果對比分析

3.1 數據說明

為了驗證WOA-CNN模型在齒輪箱故障診斷中的可行性，采用PHM協會比賽使用的齒輪箱數據PHM 2009 Challenge Data[9]。被診斷的齒輪共有3種故障：齒輪破裂、斷齒、過度磨損，每種類型的故障均對應3種齒數的齒輪：輸入齒輪/32齒、第一惰輪/96齒、輸出齒輪/80齒。因此，將故障類型設置為10種，并在公開數據集中每種類型故障分別取120 000個樣本，將120 000個樣本分成300組數據，將訓練集和測試集按3∶1比例分配，10種故障累計3 000組數據。將上述數據作為卷積神經網絡的輸入時，由于每組數據都是1×400的一維矩陣，為了提高卷積速度，特將一維矩陣轉化成20×20的二維圖像。

3.2 實驗結果

為了驗證WOA-CNN模型的分類準確率，構建WOA-BP(whale optimization algorithm-back propagation)、CNN、PSO-CNN(particle swarm optimization-convolutional neural network)、WOA-CNN 4種模型用來對比分析各類模型用于故障診斷時的優缺點。為了突出各模型的分類準確率，這里直接給出每種模型經過算法迭代后得到的最優神經網絡參數，并利用這些優化后的參數重構網絡模型。

(1)WOA-BP故障診斷模型。采用鯨魚優化算法對BP神經網絡的隱含層神經元個數、步長、訓練精度、學習率進行優化(假定該神經網絡只有1個隱含層)，即每頭鯨魚個體由一個4維向量xi=(ni,batchi,gi，ηi)組成，采用交叉熵函數作為損失函數。得到優化后的BP神經網絡的隱含層神經元個數為139，步長為41，訓練精度1e-3，學習率為0.041 725。

(2)CNN故障診斷模型。如果卷積神經網絡結構參數沒有進行優化，容易陷入局部最優解，可能導致過擬合現象。因此該模型采用前述提到的CNN結構參數，即兩個卷積層卷積核的數量k1=16，k2=8；大小s1=9×9，s2=5×5；訓練批次batch=100；學習率η=0.009，采用交叉熵函數作為損失函數。

(3)PSO-CNN故障診斷模型。粒子群算法(PSO)具有結構簡單、收斂速度快等特點，種群初始化參數為：慣性權重w=0.9；加速度因子c1=c2=2；初始粒子個數為20；迭代次數為200。由前述分析可知，初始種群中，每個粒子個體也由一個6維向量xi=(k1i,k2i,s1i,s2i,batchi,ηi)組成，用式(12)、式(13)更新粒子的位置和速度，直至找到全局最優粒子的位置。

(12)

(13)

優化后的PSO-CNN結構參數為：兩個卷積核的數量k1=16，k2=30；大小s1=8×8，s2=4×4；訓練批次batch=84；學習率η=1.063 7e-5。

(4)WOA-CNN故障診斷模型。由前所述，鯨群初始化種群個數n=20；迭代次數N=70。通過WOA算法優化CNN后得到的結構參數為(16，30，3×3，3×3，50，9.3697e-4)。將上述4種模型優化后得到的參數重構神經網絡，然后用訓練集對上述4個模型進行訓練，并通過測試集進行測試，統計5次分類精度和時間消耗取平均值，如表1所示。

表1 4種模型5次運算平均值對比

由表1可知，BP神經網絡結構較為簡單，優化后的CNN較之于未優化的深度學習神經網絡具有更高的識別準確率，但是由于模型更為復雜，運算時間也大大增加。為了說明WOA-CNN模型良好的表征性能，用T分布隨機近鄰嵌入算法[10](t-SNE)對高維數據進行降維處理，將特征聚類輸出，獲得二維分布結果，如圖2所示。

圖2 降維處理后的特征聚類輸出的二維分布結果

圖2分別表示不同迭代次數中訓練樣本分類情況，說明WOA-CNN模型在公開數據集中的分類效果較好。將10種故障類型下的加速度信號分別采集300組作為訓練集，另取70組樣本作為測試集，并且根據振動信號時域頻域波形圖提取加速度有效值、峰值、能量因數、峰峰值、頻幅值、穩定超調量、包絡解調值7種特征。將WOA-BP和WOA-CNN模型進行對比，測試結果如圖3所示。

圖3 WOA-BP模型與WOA-CNN模型對比結果

根據10次測試結果的統計，WOA-CNN模型的平均分類精度約為98.46%，而WOA-BP模型的平均分類精度約為91.71%，表明WOA-CNN模型對齒輪箱故障具有良好的分類效果，也說明卷積神經網絡在齒輪故障診斷方面有較好的準確率。

4 結論

筆者基于CNN強大的圖像識別能力，針對其網絡結構參數難以確定的問題，利用鯨魚算法優化CNN網絡結構，得到最優的卷積核大小、個數、學習率等參數，構造最優的故障模式識別分類器。通過實驗結果可以看出，針對齒輪箱公開數據集，WOA-CNN模型相比于其他算法均能夠在較少的迭代次數下達到較好的分類識別效果。