開啟教學重點的金鑰匙

洪偉

摘要：創設問題情境引入新課，就像給學生創造了一扇新知的大門，但房里最重要的保險柜也就是我們的教學重點該如何打開？作為執教者，我們不能把鑰匙直接交到學生的手中，應該引導學生自己去打開。那么究竟什么是開啟教學重點的金鑰匙呢？如何利用關鍵問題來引出教學重點，從而突出教學重點？本文將深入探討這些問題。

關鍵詞：關鍵問題 教學重點 金鑰匙

根據合肥市委、市政府《關于建設合肥綜合性國家科學中心打造創新之都人才工作的意見》（合發[2017] 17號）及市教育局相關文件精神，合肥市胡志杰教育名師工作室正式掛牌成立。數學有點冷，這是全球性的共同教學難題。我們希望用教師的教學熱情和專業知識讓學生能成為熱愛數學之美、長于數學思維、樂于數學創造的未來人才。由此我們工作室命名為“熱度空間”，研究方向是打造“熱度課堂”，如何打造？主要從六個維度打造，即教師的熱情度、備課的精準度、課堂的調控度、學生的活動度、目標的達成度、資源的融合度。本文將從備課的精準度，如何突出教學重點的角度，做一些探討。

一、關鍵問題是探究教學重點的橋梁

新課教學中，往往教學教師引出新知后，就要介紹其相關性質。但我們不能把未知的性質直接灌輸給學生，在教學重點與學生之間，我們需要給它們建立一個橋梁，可以通過關鍵問題的設置，讓學生很自然地思考問題，探究教學重點。我們強調問題設置的合理性和科學性，要讓學生能夠合理接受。

以《三角形的外角》一課的教學為例，當我們已經向同學們介紹了什么是三角形的外角后，接下來便要研究三角形外角的有關性質。在這里有兩個重要的推論，分別是“三角形的外角等于與它不相鄰的兩個內角的和”和“三角形的外角大于與它不相鄰的任何一個內角”。尤其是第一個推論，非常重要，那么如何引出這個推論呢？以下是筆者的一個教學片斷。

師：三角形的外角與內角有什么數量關系呢？

學生思考。

師（適時點撥）：如圖（見圖1），∠ACD與三角形ABC的哪個內角關系最密切？

生： ∠ACB，它們互為鄰補角， 故∠ACD+∠ACB=180°

師：那∠ACD與不相鄰的∠A、∠B有什么關系呢？

在以上的教學片段中最關鍵的問題就是“三角形的外角與內角有什么數量關系”，這個問題就可以引出我們本節課的教學重點，即“三角形的外角等于與它不相鄰的兩個內角的和”，讓學生很自然地從外角的定義過渡到外角與內角關系的探究上來。

二、關鍵問題是思維的碰撞

數學課堂是思維碰撞的課堂，可我們常常念叨現在的學生越來越懶了，不愿意思考問題，更不愿意主動提問題。那么，如何激發學生課堂上思考的積極性？如何激起思維碰撞的火花？這是我作為一名一線數學老師一直在思考的問題。我的答案是問題的設置，尤其是關鍵問題的設計。

那么如何進行有效提問？什么樣的問題又稱得上是有效的問題？有效的問題要體現在兩個方面：一是能為我所講的內容服務，二是符合學生的最近發展區。如果滿足以上兩點，那么這樣的問題就是有效的，甚至是高效的。問題本身是學生的最近發展區，那么只要學生積極思考就能思考出答案，這就是我們平常所說的“學生蹦一蹦、跳一跳就能夠到”。這里所說的關鍵問題就是有效問題或高效問題，通過關鍵問題的設置，真正鍛煉了學生的思維。下面是筆者教學過程中的一個案例。

《直角三角形全等的判定“HL”》一課中，最讓我思考的是如何引出直角三角形全等的判定“HL”，不是直接讓學生動手畫圖說明“HL”。為此，我設計了如下幾個問題。

問題1：判定兩個三角形全等需要三個元素，而判定兩個直角三角形全等還需要三個元素嗎？學生很自然地想到已經有一組直角相等，只需添加兩個元素。

問題2：那可以增加哪兩個元素呢？學生想到添加兩角，但AAA不能判定兩三角形全等;添加一邊一角，可能構成AAS或ASA，都可以判定兩個三角形全等;還可以添加兩邊，若是兩直角邊可構成SAS，能判定全等;若是一直角邊和斜邊對應相等，看著是SSA，可是這個角不是一般的角而是直角，那這究竟能否判定兩個直角三角形全等？這也就是問題3，于是很自然地就引出本節課要探討的教學重點——HL判定法。

很顯然，該例中的問題2是關鍵問題，引發學生積極思考。此時學生對“HL”究竟能否判定兩個直角三角形全等很感興趣。

三、關鍵問題揭示課堂本質內容

有時候關鍵問題不僅能引出教學重點，而且能直接揭示本堂課的本質內容，往往讓我們一下子豁然開朗，也讓學生記憶猶新。比如《合并同類項》一節中，同學們已經了解了什么是同類項，接下來如何引出合并同類項？可以設置如下問題。

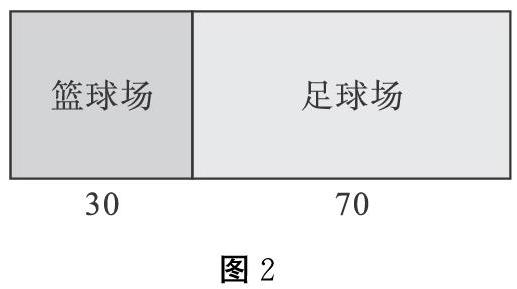
某某學校操場如圖所示（見圖2），請用兩種方法計算操場的占地面積。

生：30a+70a和（30+70）a。

很顯然操場的面積是不變的，所以可以得到：

30a+70a=（30+70）a=100a

由此可以得到什么叫作合并同類項，即把多項式中的同類項合并成一項。

本例的關鍵問題是“請用兩種方法計算操場的占地面積”，由此引出了合并同類項，而且可以通過觀察上面的計算過程，得出什么在合并，什么沒有改變。揭示出本節課的本質內容，即合并同類項的法則。

四、關鍵問題串是思維提升的腳印

關鍵問題往往不是單一的，而是由多個問題組成，簡稱關鍵問題串。通過問題串的設置，學生利用已有的知識儲備開始思考問題，思維跟著問題的節奏一步一步地提升，最終得到我們想要的結果。那么學生在這樣的教學情境下也會變得更善于動腦思考問題，同樣符合學生的最近發展區。下面以《平行四邊形的判定》為例。

在學習完平行四邊形的定義及性質之后，如何引出平行四邊形的判定呢？

筆者進行了如下設計。

想一想：

（1）平行四邊形有哪些性質？

（2）什么是平行四邊形？

（3）除了定義法以外，我們還可以添加哪些條件判定一個四邊形是平行四邊形？依照平行四邊形的性質從邊、角、對角線三個角度探究平行四邊形的判定方法。

通過以上三個問題構成問題串來引導學生去探究平行四邊形判定的方法，而不是直接告訴學生有哪些方法能判定平行四邊形。

由此可見，關鍵問題就是開啟教學重點這扇大門的金鑰匙。關鍵問題的設置要符合學生的最近發展區，讓學生能夠合理地、自然地接受新知，符合學生的認知規律，明白數學的來龍去脈。其實關鍵問題的設置就是教學生如何去思考問題，真正做到“授之以魚，不如授之以漁”。