新疆褐牛體尺典型相關分析與體重估計公式制定

王 丹，范守民，耿 娟，楊光維，董明明，胥 磊，閆夢婕，李媛媛，黃錫霞*，王雅春

（1.新疆農業大學動物科學學院，新疆烏魯木齊 830052；2.伊犁州畜牧科學研究所，新疆伊寧 835000；3.新疆維吾爾自治區畜牧總站，新疆烏魯木齊 830009；4.中國農業大學動物科學技術學院，北京 100193）

新疆褐牛為乳肉兼用牛，作為新疆地方特色的兼用牛品種，其對增加農牧民經濟收入發揮著舉足輕重的作用[1]。如今，新疆褐牛的群體規模和生產水平都得到了較大提高。在新疆褐牛選育過程中，體尺和體重測定十分重要。其中，體高及胸圍等體尺指標依靠測仗和卷尺可以比較準確方便地測得，而體重測定常常受到磅秤以及測量場地等限制，獲得大量準確數據比較困難[2]。目前規模化牛場常采用的體重估計公式是依據體高、體斜長、胸圍、管圍4 個體尺性狀而制定[3]，但是不同品種中與體重相關性最高和最容易測得的性狀往往超出這4個指標。由于受地區、品種、年齡、營養狀況、飼養管理等多種因素的影響[4]，尤其是在兼用牛的體重估計中，不同牛場的選育側重方向不同，更加不能用一種公式算出各類型牛只的準確體重。由于簡單相關系數只是孤立單個性狀之間的相關，沒有考慮X、Y 變量組內部各變量間的相關。典型相關是簡單相關的推廣，考慮了2 組變量的線性組合，實質就是在2 組隨機變量中選取若干個有代表性的綜合指標（變量的線性組合），用這些指標的相關關系來表示原來的2 組變量的相關關系。當典型相關系數足夠大時，可以像回歸分析那樣，由一組變量的數值預測另一組變量的線性組合的數值[5]。因此，為了制定出新疆褐牛成母牛體重的回歸公式，本文選取9 分制外貌鑒定中涉及的12 個性狀，采用普通及典型相關分析，分析了體重與體尺性狀之間的關系；運用多元線性逐步回歸的方法制定估計新疆褐牛成母牛體重的回歸公式，以期為新疆褐牛標準的修訂提供參考依據。

1 材料與方法

1.1 數據來源 數據來源于新疆伊犁州新源縣、昭蘇縣、尼勒克縣開展的新疆褐牛9 分制外貌鑒定標準制定過程中采集的體尺與體重實測數據，所測頭數為136 頭，均為半舍飼半放牧狀態下2～5 歲新疆褐牛成母牛的數據，本數據測量人員相同。

1.2 測定性狀 按照家畜體尺測量鑒定的方法[5]，使用測仗、臺秤、卷尺進行測量：測定指標包括體重（X1）、體高（X2）、體斜長（X3）、胸圍（X4）、胸底寬（X5）、尻長（X6）、尻寬（X7）、坐骨端寬（X8）、后腿寬度（X9）、后腿厚度（X10）、后腿高度（X11）、后腿半圍（X12）。

1.3 統計方法

1.3.1 簡單相關分析 首先對原始記錄進行錄入并剔除錯誤記錄，并應用SPSS 軟件進行簡單與典型相關性分析，研究新疆褐牛各性狀之間的相關性。其中，簡單相關系數r 參照SPSS 統計分析實用教程根據Pearson 公式計算得出[6]。

1.3.2 典型相關分析 典型相關分析采用SPSS 系統提供的宏程序（Canonical Correlation.SPS）完成，典型相關系數的顯著性采用Bartlett 的χ2檢驗[7]。此次將11個體尺性狀分為2 組，并分別做2 組變量的線性組合，進一步求解相關系數ρ。其線性組合如下：

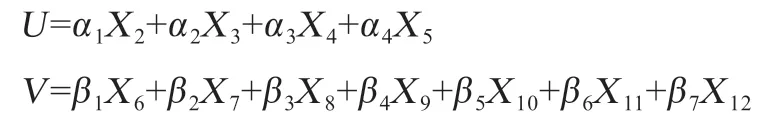
其中，U和V分別為2 組典型變量，α1、α2…α5，β1、β2…β7為典型相關系數，X2、X3…X12分別為11 個體尺性狀。

1.3.3 多元回歸方程的建立 采用一般線性模型（Linear）過程中的逐步回歸法（Stepwise）建立多元線性回歸模型，得到估測新疆褐牛體重的回歸方程，多元線性回歸分析計算模型為：

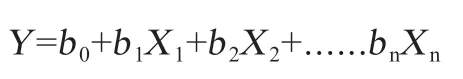
其中，Y為因變量，b0為常數，b1、b2……bn為回歸系數，X1、X2……Xn為回歸系數對應的自變量[6]。

1.3.4 估計公式驗證 為驗證新疆褐牛公牛體重回歸估計方程估測體重的準確度，選取新疆褐牛母牛共計36條數據分別代入多元線性回歸估計方程與約翰遜體重估計公式[8]計算得出估計體重，將實測體重與估計體重分別進行配對樣本t檢驗。其中，約翰遜體重估計公式為：體重=胸圍2×體斜長/11 800。

2 結果與分析

2.1 新疆褐牛主要體尺體重性狀的描述性統計 表1 為新疆褐牛體重體尺等12 個測定性狀的描述性統計量，反映了新疆褐牛在半舍飼半放牧條件下體尺體重的分布水平。根據不同性狀變異系數得知：體高變異系數最小，其次是體斜長和胸圍，表明新疆褐牛群體體型均勻度高；但是后腿厚度的變異系數最大，該性狀的選育空間大。

表1 主要體尺性狀的平均數與變異性指標

2.2 新疆褐牛體尺體重間的相關性 新疆褐牛主要體尺、體重指標間的相關系數見表2。由表2 可知，新疆褐牛體重與體高、體斜長、胸圍、尻長、尻寬、坐骨端寬具有極顯著正相關性，與體重相關性最高的性狀為胸圍，其次是體斜長與坐骨端寬；體重與后腿厚度、后腿半圍和后腿高度呈顯著正相關。

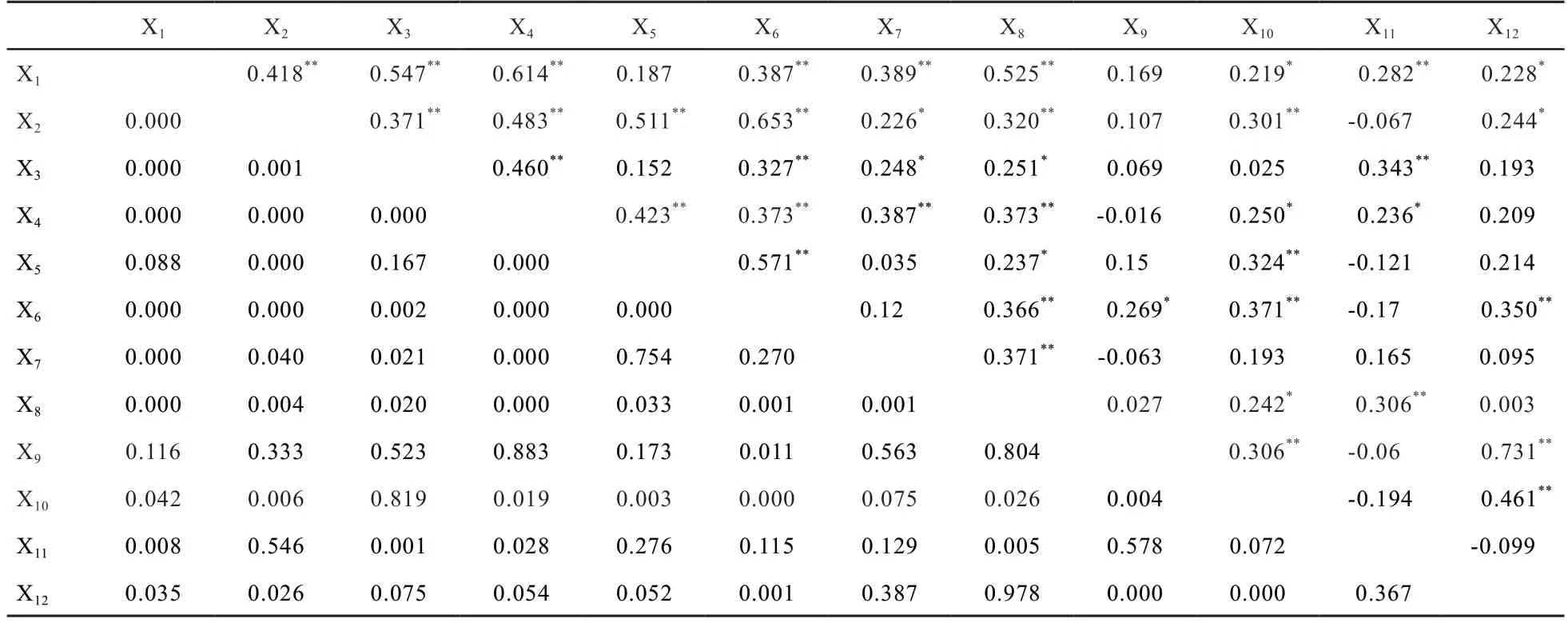
表2 主要體尺性狀指標間的相關性分析

2.3 新疆褐牛體尺的典型相關分析 對4 個典型相關系數的檢驗（表3）發現，第1 個（0.746）達到極顯著水平，第2 個（0.553）達到顯著水平，其余均不顯著。

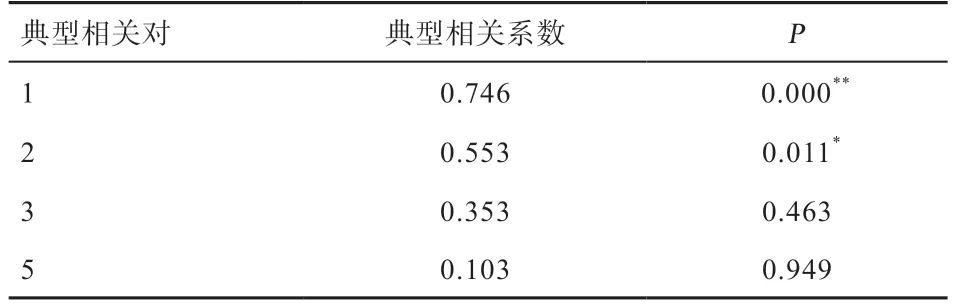
表3 新疆褐牛體尺性狀間的典型相關分析

因此，選取前2 對典型相關變量。U1、V1和U2、V2分別為2 對典型相關變量的具體構成。從2 對典型變量的構成（相關系數取絕對值論大小）可以看出，U1中X2（體高）和X5（胸底寬）的系數最大，其次是X4（胸圍）；V1中X6（尻長）的系數最大，其次是X7（尻寬），說明體軀整體結構與后軀性狀間的相關主要是由于體高和尻長的相關所引起的。U2中X5（胸底寬）的系數最大，其次是X4（胸圍）；V2中X11（后腿高度）的系數最大，其次是X7（尻寬）、X10（后腿厚度）、X12（后腿半圍）和X9（后腿寬度），第2 組典型相關說明體軀整體結構與后軀性狀間的相關還可能是由于胸底寬和后腿高度的相關所引起的。

第1 對典型變量：U1=0.01X2+0.002X3+0.003X4+0.01X5

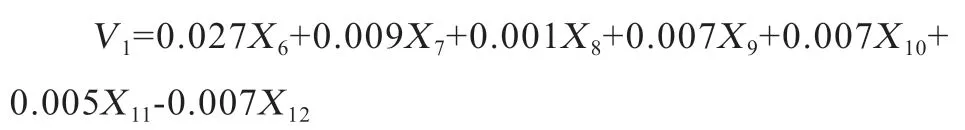
第2 對典型變量：U2=-0.004X2+0.004X3+0.009X4-0.021X5

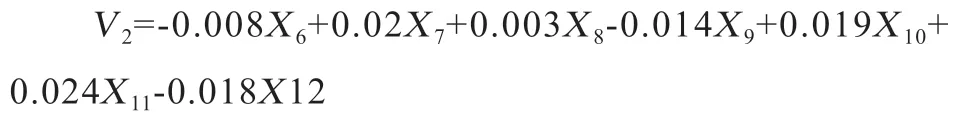
2.4 新疆褐牛體重估計公式的制定 表4 是逐步回歸最后一步的回歸方程系數表，11 個體尺性狀中進入了4個性狀（胸圍、體斜長、坐骨端寬、后腿寬度）。把表中非標準化回歸系數列數據代入多元回歸模型得到體重估計方程如下：

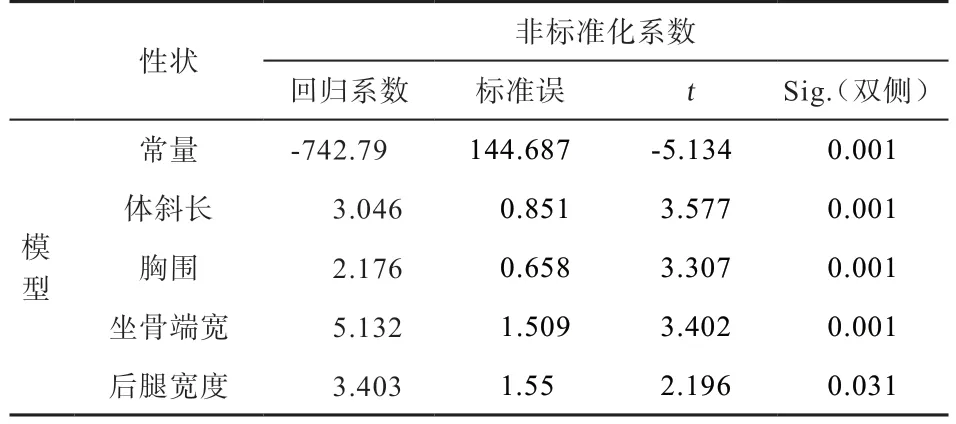
表4 逐步回歸方程系數

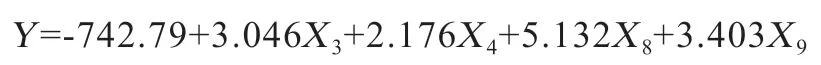
其中，Y為估計體重，X3為體斜長，X4為胸圍，X8為坐骨端寬，X9為后腿寬度。

2.5 新疆褐牛體重回歸估計方程的驗證 為驗證2.4 中得出的體重估計方程估計體重的準確度，選取新疆褐牛母牛共計36 頭個體記錄，通過代入上式計算得出估計體重。通過SPSS 19.0 軟件對實測體重和估計體重2 組數據進行配對樣本t檢驗，以μ=0 的t分布函數95%區間內來判斷二者之間的差異性，實測體重與回歸估計體重之間的相關系數為0.762，配對樣本t檢驗結果如表5所示，實際體重與估計體重之間無顯著性差異。

表5 實測體重與回歸估計體重樣本配對t 檢驗

通過SPSS 19.0 軟件對約翰遜公式計算得出估計體重與實測體重2 組數據之間進行配對樣本t檢驗，以μ=0 的t分布函數95%區間內來判斷二者之間差異性，約翰遜公式估計體重與實測體重差異不顯著，相關系數為0.5，對比證明新疆褐牛母牛體重估計公式具有統計學意義。

3 討 論

3.1 新疆褐牛體尺體重簡單相關分析 新疆褐牛體重與體高、體斜長、胸圍、尻寬、尻長、坐骨端寬、后腿高度等呈極顯著正相關，與體重相關性最大的體尺性狀為胸圍、體斜長、坐骨端寬與體高，這與多元線性逐步回歸分析中最終進入的4 個性狀結果一致。本文選取的11 個性狀中與體重相關性最大的是胸圍，這與鄧由飛[9]等人對肉牛體尺指標與體重的相關分析結果相同。付雪峰[10]對舍飼新疆褐牛犢牛的體尺相關性分析結果表明4 個體尺間均存在極顯著的正相關（P＜0.01）。在其他品種的乳肉兼用牛的體尺體重研究中，魯西黃牛與體重相關性最大的性狀為胸圍[9]，大額牛體重與體斜長和胸圍呈現極顯著正相關[10]；閩南黃牛重與體高、體長、胸圍、十字部高均存在極顯著正相關[11]，以上研究結果均與本研究結果相似。

家畜體尺不僅反映家畜的體軀結構、發育水平，還反映畜體組織器官的發育狀況及體重，例如胸圍較大的牛心肺容積較大且血液循環較好，因此胸圍大小可以作為外貌鑒定的一項指標。家畜體尺還可以反映出個體潛在生產性能，相關性分析發現，體重與體尺指標間存在顯著的線性關系，胸圍較大的牛體重也較大，相關系數為0.642，在選取后備牛育肥時，可將常規的四大體尺與本文中涉及的后軀性狀結合起來。此外，還可根據不同養殖場的育種規劃，合理利用各性狀間的相關性制定選種選配計劃。

3.2 新疆褐牛各體尺性狀的典型相關分析 典型相關分析是反映各指標之間的整體相關性的多元統計分析方法，在牛[12]、羊[13]、豬[14]、禽[15]等物種中均有廣泛應用。其基本原理是：為了從總體上把握2 組指標之間的相關關系，分別在2 組變量中提取有代表性的2 個綜合變量U1和V1（分別為2 個變量組中各變量的線性組合），利用這2 個綜合變量之間的相關關系來反映2 組指標之間的整體相關性。

利用典型相關可以分析畜禽體尺與體重，體尺與生產性能、生理與行為特征之間的關系[12-15]，本研究通過對新疆褐牛11 個體尺性狀分組，2 組變量分別代表體軀結構與后軀結構，得到了4 個典型相關系數值，其中共2 對呈現出顯著性，并且典型相關系數值分別是0.746、0.553，意味著2 組體尺之間有著典型相關關系，后續將重點考慮呈現出顯著性的典型變量。本研究結果表明，與尻長和尻寬相關性最大的是體高與胸底寬，簡單相關表明體高與胸底寬呈極顯著正相關，這說明新疆褐牛體高越高且胸底寬越寬，則尻長和尻寬越大，反之亦然，與王永齊等人分析結果一致[16]。由于本研究僅有單次體重測量數據，所以未能將體尺與體重數據進行典型相關分析。。

3.3 新疆褐牛的體重估計公式 新疆褐牛體重估計公式為：Y=-742.79+3.046X3+2.176X4+5.132X8+3.403X9。通過逐步分析法，新疆褐牛的12 個體尺性狀中，胸圍、坐骨端寬、體斜長、后腿寬度4 個性狀極顯著。同樣應用逐步回歸法在中國西門塔爾牛體重回歸公式的制定中，其實測體重和約翰遜公式估重結果進行比較結果顯示逐步回歸結果優于約翰遜公式[17]。由于此次9 分制外貌鑒定相關的所有性狀中沒有測量管圍，因此，本文沒有就這2 種不同的公式估計新疆褐牛體重的準確度進行對比，這還有待于進行更進一步分析。但是，針對管圍和坐骨端寬這2 種不同的性狀在實際生產中的測量難易程度比較，管圍的測量方法為在左前肢管部上三分之一處[18]，用卷尺量取周徑，測量人員在進行管圍測量時面對意外傷害的風險較測量坐骨端寬高，相較而言該體重估計方程更加實用高效。在生產中，選擇體型外貌優秀的公、母牛選配組成核心群很有必要，這樣可以鞏固已取得的成果，進一步提高牛群質量[19]。新疆褐牛為乳肉兼用牛，不同的地區對其產品的需求不同，選育的側重方向也不同。在伊犁地區，新疆褐牛選育側重于肉用方向[20]，采用放牧加補飼的飼養模式，在其他地區實際生產中應當結合群體的特征選取合適的模型加以應用。

4 結 論

本研究通過相關分析表明，體重與體尺之間呈不同程度的正相關關系，新疆褐牛體尺指標對體重的最優回歸方程為Y=-742.79+3.046X3+2.176X4+5.132X8+3.403X9。經過檢驗該方程具有統計學意義，此新疆褐牛體重估計模型可應用于在實際生產過程中對半舍飼半放牧狀態下新疆褐牛體重的估測。