一種基于損傷等效原理的PSD路譜生成方法

王瑋，周肖飛，陳文斐，翟云飛

(1. 西安交通工程學院，陜西 西安710300；2. 陜西汽車控股集團有限公司，陜西 西安710200)

0 引言

在車輛耐久分析中，往往通過靜力學分析求解單位載荷作用下的結構響應，疊加道路載荷譜后形成應力時間歷程曲線求解疲勞壽命。這種方法簡單直接，得到了大量的應用[1]。也有將載荷譜直接加載到分析部件上，求解瞬態動力學響應，以考察結構的動態特性對疲勞的影響，使疲勞結果更接近真實[2]。但采用瞬態方法往往帶來更多的計算量，在工程中需要一種能夠保證精度且更快速的分析手段。

在結構安裝位置處布置加速度傳感器獲取載荷激勵，通過傅里葉變換(FFT)轉換為功率譜密度曲線(PSD)，然后通過隨機響應分析估算結構的應力范圍，進而計算結構的疲勞壽命[1]。這種方法計算效率較高，精度滿足需求，故而被廣泛應用。但隨著車輛耐久試驗的復雜化，每次試驗往往包含多種路面工況，由于不同路面的激勵頻率和幅值都有所不同，該隨機過程無法用平穩過程描述。因此在進行傅里葉變換時會對PSD幅值進行平均。

圖1為一個典型的車輛耐久試驗路譜，其中搓板路激勵的時間較長，頻率較低，幅值較小，而比利時路面激勵的時間極短，頻率較高，幅值極大。在這種情況下，直接的傅里葉變換會導致搓板路激勵和比利時路激勵在相同頻率時出現幅值平均，從而導致最終的損傷值偏低。

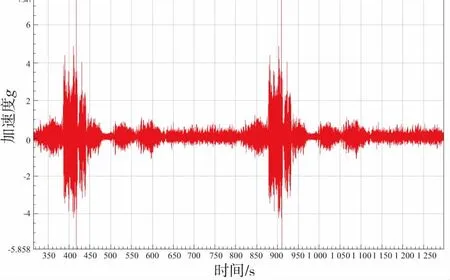
圖1 某路試加速度譜

本文提出了采用損傷等效原則的PSD生成方案，實現轉換前后載荷幅值和頻率的一致，為解決復雜路面激勵提供了一種解決方案。

1 基于FDS的PSD生成方案

1.1 處理流程

基于FDS的PSD生成，就是通過原始載荷譜計算損傷譜，再由損傷譜轉換為PSD譜。在轉換過程中必須遵守兩個原則：第一，必須保證轉換前后對結構造成的疲勞損傷是一致的；第二，必須保證在轉換前后載荷的幅值是相同的。其轉換流程如圖2所示。

圖2 基于FDS的PSD譜生成流程

1.2 沖擊響應譜

1932年，美國工程師Biot通過研究地震對相關結構的損傷時發現：單自由度振子系統的響應由其自然頻率主導，低于自然頻率的部分表現為準靜態效應；超出自然頻率的部分隨著激勵頻率的增加會逐漸減弱；在自然頻率附近，結構的振動幅值會大幅度增加。此時，其幅值大小由系統阻尼決定，動態響應與靜態響應的比值稱之為幅值比Q，當阻尼為0.05時，幅值比Q=10[3]，如圖3所示。

圖3 激勵頻率與加速度響應的關系

將時域載荷譜與該頻率響應函數相乘，得到在當前自然頻率下的時域響應信號。采集該響應信號的最大值，可描繪出結構最大響應與自然頻率之間的關系曲線(此時只為一個點)，即為單自由度振子系統的響應譜曲線(response spectrum, RS)

將其推廣到多自由度系統上，由于多自由度系統具有多個自然頻率，就需要重復上述分析過程，分別計算載荷譜在不同自然頻率下的最大響應，將所有的最大響應點相連，可獲得多自由度系統最大響應與頻率的關系，即為沖擊響應譜(shock response spectrum，SRS)。其計算流程如圖4所示。

圖4 沖擊響應譜獲取流程

1.3 損傷譜的獲取

受沖擊響應譜的啟發，Halfpenny提出了利用時域信號計算損傷譜的方法，將各個頻率下的結構響應通過雨流計數統計，直接加載到S-N曲線上，可獲得載荷在各個頻率下的損傷值。在獲得某個自然頻率下的時域響應曲線后，直接用該響應曲線進行雨流統計，然后計算其累計損傷，即可得出損傷譜(fatigue damage spectrum，FDS)[4]，如圖5所示。

圖5 損傷譜獲取流程

其方法分為4個步驟：

1)將激勵信號加載在單自由度系統上，計算在某個自然頻率下的載荷時間歷程；

2)對該載荷時間歷程進行雨流計數，計算該頻率下的累計損傷；

3)多次重復前兩步操作，計算多個頻率下的累計損傷；

4)將損傷與頻率描繪在平面坐標系中，即為損傷譜。

損傷譜可以清晰地表達出在某個頻率下載荷對結構產生的損傷值大小，可以更準確地反映出載荷對結構的破壞能力。

1.4 極端響應譜

對于時域載荷而言，沖擊響應譜能夠清晰地給出結構最大響應與頻率的關系，但在實際中，很多載荷都是隨機性的，使用PSD譜表達載荷分布更為準確。如何用類似與SRS的方式簡單地表達出結構的最大響應，1953年，Miles給出了結構響應的均方根值(RMS)與頻率的關系式[5]，假設激勵為高斯分布，則對于加速度而言

(1)

對于位移而言

(2)

其中：Q為幅值比；fn為結構的自然頻率。

1978年，Lalanne通過統計發現，對于窄帶的激勵而言，其激勵分布更偏向于瑞利分布(rayleigh)，故需要將上式進行修正[6]，修正后的方程如式(3)和式(4)所示，對于加速度而言

(3)

對于位移而言

(4)

此即為極端響應譜(extreme response spectrum, ERS)。

1.5 極端響應譜的損傷曲線估計

2002年，Lalanne基于極端響應譜的估計，提出了基于ERS的損傷曲線方程，使得可以直接從PSD曲線中獲取FDS[7]，其結構如下：

(5)

其中：fn為結構自然頻率；K為結構剛度；C和b為材料疲勞參數；Γ為伽馬方程，其具體形式為

(6)

1.6 基于FDS的隨機譜合成

式(3)表示由PSD譜計算極端響應譜的過程，式(5)表示極端響應譜和損傷譜的關系，將兩方程進行反推，即可獲得從損傷譜計算極端響應譜的方法。而損傷譜可直接將時域載荷譜通過雨流計數獲取。如此，就打通了從時域譜如何獲取PSD譜的全過程，但在這個流程中，需要考慮安全因子的影響。

安全因子可用載荷大小與材料疲勞強度的比值來表達：

(7)

實際工程中，施加在結構上載荷往往表現出明顯的隨機性，由于材料的疲勞性能同樣存在隨機性，因此安全因子不僅要考慮載荷大小和疲勞強度，同時還需要考慮存活率的影響。

圖6中，x軸表示應力大小，y軸表示出現概率。假設隨機載荷和材料疲勞強度均呈現高斯分布，那么兩條概率分布曲線的重合區域即為結構在該隨機載荷作用下的失效率，非重合區域則為存活率。顯然兩者存在以下關系：失效率+存活率=1。

圖6 材料的失效率

對于高斯分布，安全因子與存活率可用下式表達：

(8)

其中：a′表示存活率；VR表示強度變化率；VE表示載荷變化率，其可用下式表達：

(9)

(10)

其中σR和σE分別是材料疲勞強度和載荷的標準差。

將式(5)反推并考慮安全因子的影響，可獲得從FDS求解PSD的方程

(11)

2 基于FDS的PSD隨機疲勞分析

某商用車電瓶箱結構如圖7所示。

圖7 某商用車電瓶箱示意圖

在約束位置加載幅值為1g的正弦波，計算頻率從1Hz～200Hz的掃頻響應。圖8為521號單元在3個方向的頻率響應曲線。

圖8 單元應力頻響曲線

在電池包根部粘貼加速度傳感器，采集到根部的加速度載荷如圖9所示。

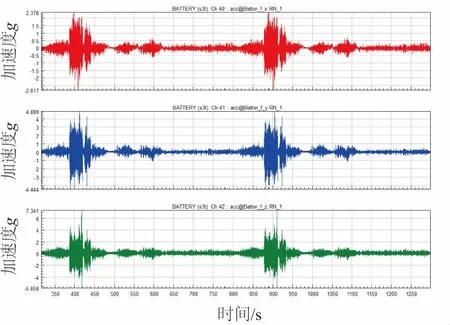
圖9 電瓶箱根部的加速度譜

由于路譜具有很強的隨機性，因此常采用隨機振動的方式計算結構響應。對x方向的譜分別采用直接轉換的方式和FDS轉換的方式轉成PSD譜，如圖10所示。

圖10 兩種方式生成的PSD譜

可以看出，由于存在幅值的平均，采用傅里葉變換直接生成PSD譜的最大值明顯被削弱了，采用FDS轉換的方式計算出來的PSD譜在低頻段(3Hz以內)偏小，而在高頻段(10Hz以上)偏大，這是由于路譜在低頻段能量偏低但時間較長，在高頻段能量較大但時間偏短造成的。

在疲勞分析軟件中，分別加載直接轉換的PSD譜和采用本文方法轉換的PSD譜計算結構的疲勞壽命，結果如圖11所示。

圖11 兩種載荷下電池包的壽命云圖

由圖11可知，采用兩種PSD譜計算的壽命分布趨勢基本一致，但量級上存在較大差異，采用直接轉換PSD譜計算的最小壽命為5.2×106次循環，采用本文方法計算的電池包壽命為2003次循環。鑒于該最小壽命往往出現在約束周邊的應力集中位置，真實結果應大于最小壽命，對結構重點部位壽命進行采集，與試驗結果對比如表1所示。

表1 計算結果與試驗結果對比 單位：次

由表1可知，采用本文方法轉換的PSD譜在結構上產生的損傷要遠大于直接轉換PSD譜的損傷，與實際試驗結果也比較吻合。

3 結語

在工程實際中，大多數路試路譜都很復雜，而且呈現出明顯的隨機性，采用傳統方法計算疲勞壽命需要對路譜進行分割，單獨計算各路段的三向損傷，然后將損傷進行線性疊加，這帶來了巨大的工作量。通過FDS進行PSD譜的轉換，可以大幅度縮減重復工作，并且保證轉換前后損傷的統一，對工程應用有很大的幫助。