空間自由曲線的相似性比較方法

王道俊，王洪申

(蘭州理工大學 機電工程學院, 甘肅 蘭州 730050)

0 引言

在計算機視覺和模式識別中，形狀相似性度量是一個重要的研究課題，在眾多領域中具有廣泛的應用，如圖像檢索、文字識別、目標識別、醫學圖像分析、人臉識別、機器人導航以及傳感器網絡等。在形狀相似性度量問題中，兩條曲線的相似性度量是基本問題。在進行模型的相似性評價時，研究人員通常對模型進行特征提取，即提取出能夠代表模型本質特征的因素，再通過對模型特征的相似度計算評價模型的相似性。特征提取方法較多，其中形狀分布算法[1]因其原理直觀，性能魯棒而被廣泛采用。趙俊莉等[2]以平均測地距離作為評價依據，研究3D人臉形貌的相似性比較；馬元魁等[3]以形體的形狀分布曲線作為識別圓環體間形狀差別的評價度量；ALCZAR J G等[4]運用曲線的曲率和撓率評價曲線間的相似性；BUCHIN K等[5]通過計算Fréchet 距離作為相似性度量，研究了運動曲線的相似性；呂科等[6]以解決空間曲線匹配來達到文物碎片的復原，運用輪廓線的哈希矢量分析曲線段的相似度。王堅等[7]針對封閉輪廓曲線，計算各采樣點的弗朗內特標架和曲率值，利用曲率形成匹配點對，再通過對齊弗朗內特標架獲得匹配矩陣，取匹配誤差最小的矩陣作為最優匹配矩陣，實現空間曲線的匹配。孫曉鵬等[8]運用Minkowski距離作為相似測度，實現基于統計形狀特征的三維耳廓點云識別。王洪申等[9]利用曲線的曲率分布描述空間曲線的幾何特征，并以此衡量三維自由曲線的相似程度。

現有的形狀分布算法通常是：1)定義一個函數，在三維模型上計算該函數值；2)統計函數值，將三維特征描述成函數值的二維分布圖；3)根據二維分布圖之間的距離作為相似程度依據。本文為了研究自由曲線間的相似性，計算曲線上的點到曲線形心的歐式距離作為描述函數，并將多個距離組成集合作為曲線的形狀描述特征，然后直接計算集合之間的EMD(earth mover’s distance)距離，并以該距離作為評判相似性的依據。省去了常規形狀分布算法的第2)步函數值的統計過程，從而減少了信息損失，更簡潔、直觀地實現了相似性的評價。

1 平面曲線和空間曲線的相似性評價算法

EMD即推土機距離，最初是為了解決運輸問題[10]，該算法能通過一次線性規劃計算出兩個大小不同(或相同)的幾何或向量的距離，可用于測量不同維特征向量之間的相似性。本文以沿曲線等弧長方向均勻取點，計算每個點到曲線質心的歐式距離，以該距離作為曲線的特征，使用EMD算法計算兩個曲線特征之間的距離，以該距離的大小描述曲線的相似性。

設MC={Curve1,Curve2}是含有2個元素的一個自由曲線集合，通過運算比較集合中元素之間的相似性。算法步驟如下：

1)沿自由曲線Curvei(其中i=1時，表示自由曲線1，i=2時，表示自由曲線2)等弧長取相同的點數n，得到點集合表示為Pij={Pij，i=1，2；j=1，2，3，…，n；}，獲得每個點坐標Pij(xi，j，yi，j，zi，j)。

2)計算自由曲線的質心Mi(i=1,2)，計算質心公式寫成坐標分量形式，如下：

(1)

其中n為三維點的數量。得到Curve1的質心M1(x1，0，y1，0，z1，0)，Curve2的質心M2(x2，0，y2，0，z2，0)。

3)利用歐氏距離公式，計算自由曲線上等弧長所取每個點與質心Mi的距離，記為|pijMi|，得到自由曲線上等弧長取點距離的集合Di={di=|pijMi|,i=1,2;j=1,2,…,n}；

4)步驟3)中計算的每個距離集合代表了一條曲線特征，計算兩個距離集合的EMD值，EMD值越小，曲線越相似。

記作：

δsim(Curve1,Curve2)=EMD(D1,D2)

(2)

2 算法驗證實例

2.1 實驗設計

為驗證本文曲線相似性評價算法的性能，構造如表1所示的3組平面自由曲線模型和表2所示的3組空間自由曲線模型。其中：表1所示的3組平面曲線中，第1組為形狀有微小差異的3條平面橢圓曲線，用人眼的直觀相似性評價，曲線2和曲線3更相似，計算值應滿足式(3)；第2組為形狀有微小差異的平面B樣條開曲線，用人眼的直觀相似性評價，曲線1和曲線2更相似；第3組為形狀有微小差異的平面B樣條閉曲線，用人眼的直觀相似性評價，曲線1和曲線2更相似。第4、第5組為形狀有微小差異的空間B樣條開曲線，第6組為形狀有微小差異的空間B樣條閉曲線。第2組至第6組實驗，以人眼直觀觀察，實驗結果應滿足式(4)。實驗中，分別在每條曲線上以等弧長方法取相同數量的點(設取點數量為m)，計算所取點與曲線質心的歐氏距離，作為EMD度量的參數，將平面曲線和空間曲線上得到的歐氏距離的依次帶入式(2)，計算兩兩曲線的EMD值。

δsim(Ellip2,Ellip3)<δsim(Ellip1,Ellip2)<δsim(Ellip1,Ellip3) (3)

δsim(Curve1,Curve2)<δsim(Curve2,Curve3)<δsim(Curve1,Curve3)

(4)

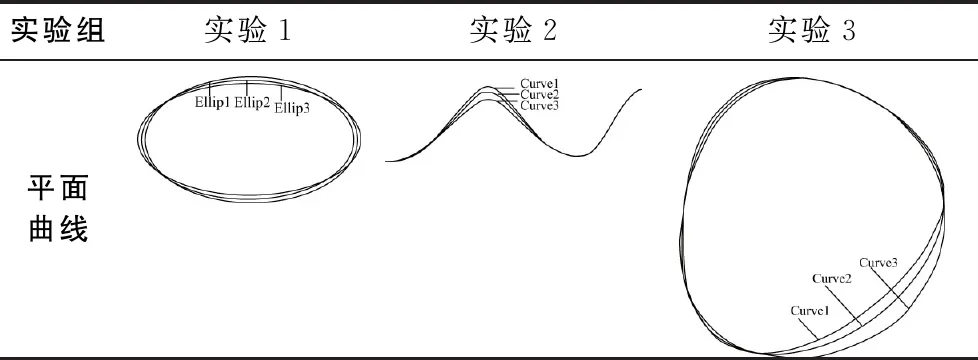
表1 算法對平面曲線有效性驗證實驗

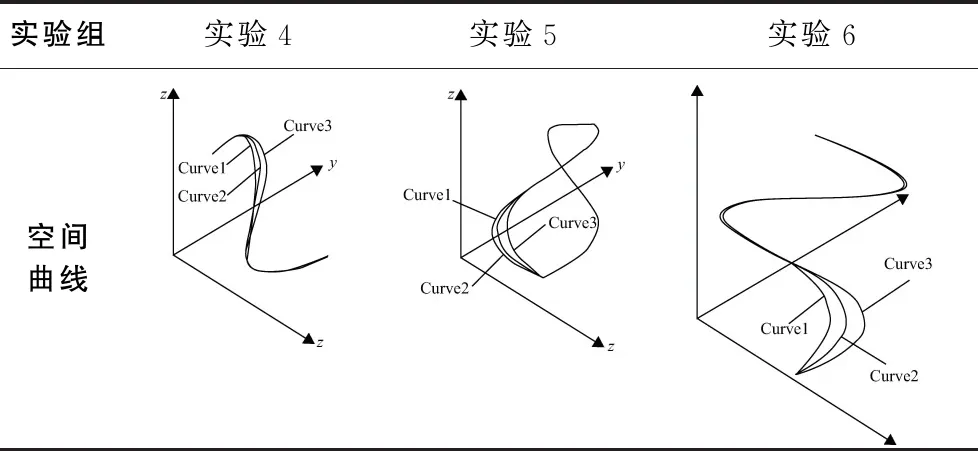
表2 算法對空間曲線有效性驗證實驗

2.2 實驗結果與討論

1)針對平面曲線的算法有效性驗證

應用構造的第1-第3組平面曲線，設計3組實驗，驗證算法的有效性與可行性。由式(2)計算兩平面曲線的EMD值，根據所取點數的不同，得到表3所示的實驗數據。所得實驗數據滿足式(3)、式(4)，與人的直觀評價一致。

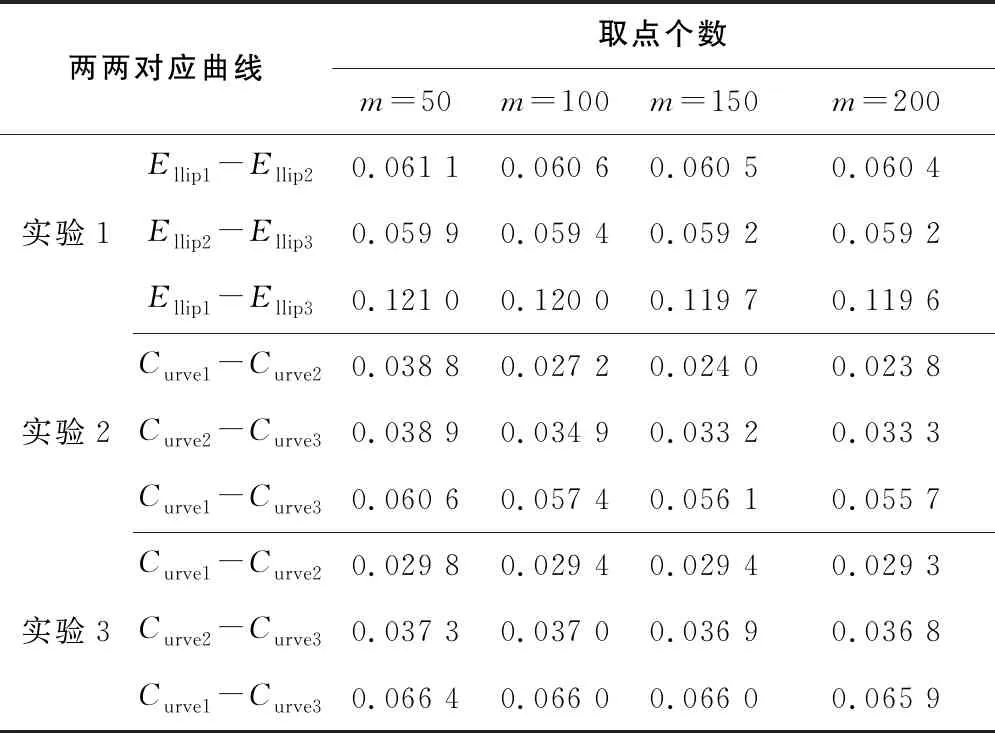
表3 算法對平面曲線有效性實驗數據

2)針對空間曲線算法有效性驗證

運用構造的第4-第6組空間曲線，設計3組實驗，驗證算法的有效性與可行性。由式(2)計算兩曲線的相似度量值，根據所取點數的不同，得到表4所示的實驗數據。所得實驗數據滿足式(3)、式(4)，與人的直觀評價一致。

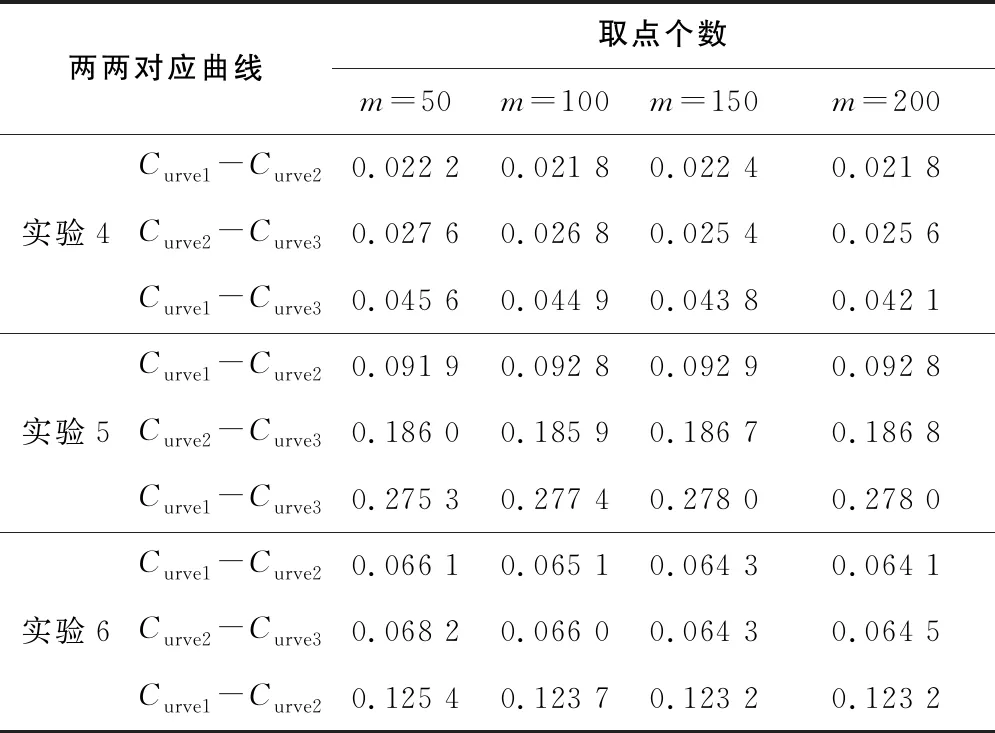
表4 算法對空間曲線有效性實驗數據

3)算法魯棒性驗證

應用構造的第3組平面曲線的Curve1、Curve2和第5組空間曲線的Curve1、Curve2，分別設計3個實驗，驗證算法對平移和旋轉的魯棒性。組號分別記為X-Ⅰ、X-Ⅱ、X-Ⅲ(X取3、5)。X-Ⅰ組不進行任何變換，比較兩曲線的相似性；X-Ⅱ組曲線Curve1與Curve2分別平移不同的距離，比較兩曲線的相似性；X-Ⅲ組曲線Curve1與Curve2分別進行旋轉變換，比較曲線的相似性。實驗結果如表5所示，X-I組和X-II組的相似值相同，表明相似性評價結果與曲線的平移無關；X-I組和X-III組的實驗數據對比可知，相似性評價結果與曲線的旋轉無關。因此，算法具有平移、旋轉不變性。

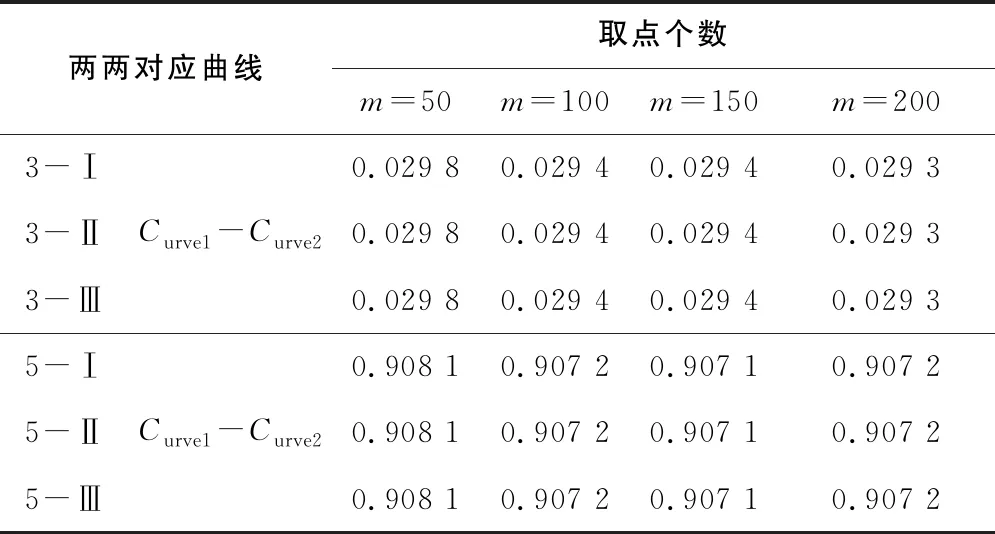
表5 算法魯棒性實驗數據

3 結語

本文提出了曲線的相似性評價算法，適用于平面曲線和空間曲線。首先在曲線上取點計算該點到曲線質心的歐氏距離，作為該曲線的特征，然后用EMD算法計算曲線特征的距離，用于度量空間曲線的相似性，計算簡便，方法可靠。算法評價的空間曲線相似性結果符合人的感官判斷，能夠很好地反映空間曲線的相似程度。通過大量的實驗驗證，算法可行有效。