飛機艙門開關機構數字化模型構建技術研究

吳揚，張樂，裘旭冬，周石恩, 陸玥, 朱駿

(1. 上海飛機設計研究院，上海 201210； 2. 上海無線電設備研究所，上海 201109)

0 引言

飛機艙門機構系統是飛機的主要機構系統之一(圖1)，其能否完成預期的功能將直接關系到飛機的飛行安全性[1]。作為艙門系統的主要測試門類之一，艙門開關機構聯動姿態測試是一項流程復雜、工作量大的工程。通過仿真模擬與物理測試相結合的方式，并且未來逐步以虛擬試驗為主，物理試驗為輔，是提高測試效率的有效途徑[2]。在投產和正式試驗啟動前對試驗過程進行預演和分析，能夠提高試驗設計的準確性，對于減少試驗成本、縮短試驗件結構優化周期具有重要意義[3]。

圖1 飛機艙門示意圖

傳統機構運動仿真方法大都是以特定運動副來約束組成零件，一般只適用于較為簡單的機構，而對于飛機艙門開關機構這種零件層級多、串并聯混合的復雜系統則難以模擬[4-5]。本文通過構建簡單機構的數學模型及機構間的串并聯關系，以驅動件運動參數為自變量，逐層求解各個被動件運動表達式，可視化顯示任意時刻的艙門狀態。

1 系統介紹

1.1 飛機艙門開關機構

飛機艙門開關機構由凸輪手柄傳動機構、鉸鏈臂機構、鎖鉤開閉機構等眾多子機構組合而成[6-7]，如圖2所示。本文研究對象艙門為外開式，整個開門過程包括艙門抬升和艙門平移兩個步驟[8]。打開后的艙門與機身平行，其機構狀態如圖3所示。

圖2 艙門開關機構主要組成部分

圖3 艙門開啟后狀態

1.2 Visual Components軟件系統

所采用的軟件系統為Visual Components軟件，簡稱VC。VC是全方位的數字化工廠仿真軟件，集離散物流仿真模擬、機器人離線編程以及PLC虛擬調試三大功能于一體。VC支持絕大多數的CAD格式文件導入，包含豐富的組件庫，具有獨創的PnP即插即用功能，可實現機構組件的屬性、行為定義和運動仿真。

2 飛機艙門模型前處理

2.1 艙門CAD模型導入

飛機艙門一般是在Catia等專業建模軟件中創建，然后導入到VC軟件中。為防止結構樹錯亂以及格式轉換問題，將Catia模型分為多個cgr格式部件結構，再導入VC軟件中。以艙門把手為例，在VC軟件界面中選擇導入“幾何元”選項，如圖4所示。在VC軟件的“建模”模塊，可以看到把手部件的結構樹下包括多個子實體。由于后續整個把手保持相同的運動，需使用“組合”功能將把手對應實體部分合并為一個實體，如圖5所示。

圖4 CAD零件導入VC界面

圖5 部件結構幾何實體合并

2.2 機構關節提取及層級確定

選擇把手合并后的實體并利用“提取鏈接”功能生成結構關節，它包含部件坐標、部件名稱、部件偏移量以及關節屬性等屬性，如圖6所示。將把手作為主動驅動件，運動方式為旋轉，將把手零件坐標系調整至y軸與旋轉軸重合，此時旋轉方向為+y軸，新建伺服控制器Servo Controller來進行驅動，關節名稱為J1。

圖6 把手關節提取與屬性編輯

艙門開關機構是由眾多子機構通過串并聯方式組合完成艙門的開啟和關閉。圖7為艙門鉸鏈臂子機構層級圖。通過對多層級的機構串并聯關系的分析，確定從動件運動的相對關系，才能夠理清艙門開關機構工作機理，又有利于更高層級從動件運動表達式的求解。

圖7 艙門開關機構整體層級表示

3 機構關節運動表達式求解

3.1 凸輪曲柄機構

圖8是由把手、內凸輪部件、搖臂以及其他固定件組成的凸輪曲柄機構。內凸輪部件與手柄具有相同的運動狀態。第一階段由于內凸輪前半部分圓弧與把手旋轉軸線一致，此時搖臂末端銷柱(與搖臂運動形式一致)保持不動；第二階段則驅使銷柱沿內凸輪后半直線部分運動，表現為搖臂繞其軸線的旋轉運動。以下求解第二階段求解搖臂的運動表達式。

圖8 凸輪曲柄機構

將凸輪曲柄機構內凸輪和搖臂投影到二維平面，如圖9所示，其中O1和O2分別為搖臂和內凸輪的旋轉中心，以O2為圓心，O2O1為y軸建立坐標系。第二階段初始狀態時，C點和A點分別為內凸輪直線部分的起點和終點；當把手旋轉一定角度J1(∠AO2B)時，C點和A點分別運動到E點和B點，此時銷柱由C點運動到D點，∠CO1D(記為θ)即為搖臂的旋轉角度。定義各個尺寸和間距如下：O1O2=h，O2C=O2E=R1，O2A=O2B=R2，O1C=O1D=R3，AC=BE=L，∠AO2C=∠BO2E=α，∠CO2O1=β。

圖9 凸輪曲柄機構二維投影分析圖

通過圖9可以看出，θ的大小取決于線段CD的長度x，可以根據余弦定理求解，如式(1)所示。在VC軟件中，定義了三角函數sssad用來快速求解三角形參數，則式(1)可以轉化為式(2)的形式。點C和點A的坐標位置可通過測量固定長度項后計算獲得，如式(3)所示。

(1)

θ=sssad(x,R3,R3)

(2)

(3)

式(3)中的角度α和β為定值，可用尺寸參數計算獲得，如式(4)所示。

(4)

根據旋轉變換方法，銷柱從初始位置(xD,yD)隨搖臂轉動角度θ后，到達新的位置(x′D,y′D)，二者存在式(5)所示關系，其中(x0,y0)為旋轉中心坐標。

(5)

銷柱初始位置在AC連接的直線上，銷釘與搖臂旋轉中心的距離保持不變，即：

(6)

(7)

聯立方程式(5)、式(6)、式(7)即可求得第二階段搖臂旋轉角度θ隨把手轉角J1的數學表達式，而第一階段它的值為0，因此其運動方式為分段函數，曲線如圖10所示。

圖10 搖臂隨把手轉動曲線圖

3.2 四連桿機構

圖11是由搖臂AB、連桿BC和套筒CD組成的四連桿機構，在ABCD平面內，搖臂的轉動中心A和套筒的轉動中心D相對位置保持不變，初始狀態時四連桿長度a、b、c、d以及各邊之間的夾角都可以通過測量得到，t=0時刻搖臂AB與AD的夾角大小記為A0。當搖臂AB驅動一定角度A(與3.1節的角度θ一致)時，問題轉化為求解連桿BC和套筒CD的對應運動表達式。由于連桿BC繞B點運動角度參考對象為搖臂AB，因此連桿BC與搖臂AB間層級關系為串聯；套筒CD繞D點運動角度參考對象為大地，因此套筒CD與搖臂AB間層級關系為并聯。

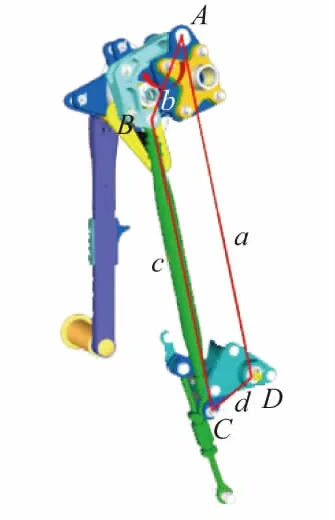
圖11 艙門提升四連桿機構

四連桿機構的運動求解主要是通過余弦定理，假設BD的長度為e，在運動過程中e的大小會隨著搖臂擺動角度而變化。當搖臂轉動角度A時(此時搖臂AB與AD的實際夾角為A+A0)，二者存在關系：

e=a2+b2-2·a·b·cos(A+A0)

(8)

連桿BC轉動角度B由∠DBA和∠DBC相加得到，因此可以求得其表達式，如式(9)所示。同理，套筒CD的轉動角度D表達式如式(10)所示。

(9)

(10)

在VC軟件中，定義了特定的函數sasssa1用來快速求解四連桿機構參數，連桿BC轉動角度B和套筒CD的轉動角度D可以表示為式(11)。

(11)

式中degree和radian分別是VC軟件中弧度轉角度和角度轉弧度的函數。

對于存在“交叉”現象的特殊四連桿結構(圖12)，由于使用余弦定理得到的表達式與式(8)和式(9)形式不一致，因此不能直接使用四連桿機構計算函數sasssa1，可通過兩個三角函數sssad組合求解。

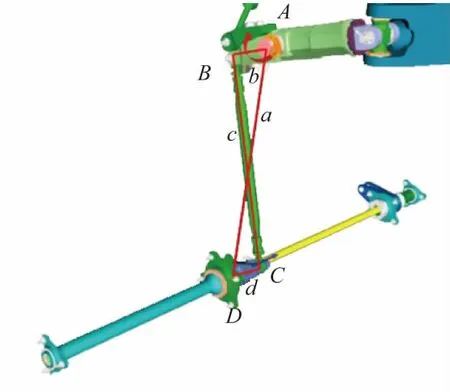
圖12 “交叉”四連桿機構

在“交叉”四連桿機構中，BD長度e與式(7)完全一致，連桿BC轉動角度B由∠DBA和∠DBC相減得到，同理，套筒CD的轉動角度D由∠BDC和∠BDA相減得到，將其用VC軟件自帶的sssad表示，如式(12)所示。

(12)

4 結語

本文利用簡單機構的復合構建了艙門開關機構的數字化模型，以表達式形式準確表示任意時刻機構組成零部件的所在位置，實現艙門開關過程的可視化。結果表明：艙門提升臂、搖臂等關鍵結構件隨把手轉動的角度與實際一致；且艙門提升高度以及平移幅度也與測量結果相同；證明了本文方法能夠準確模擬飛機艙門開關情況。