某新型轉膛自動機換向器的疲勞壽命分析

翟嘯雷，戴勁松，王茂森，舒昌旭，寧春交

(1. 南京理工大學 機械工程學院，江蘇 南京 210094； 2. 國營第152廠，重慶 400071)

0 引言

轉膛自動機是指擁有一個平行于炮膛軸線可以轉動膛體的自動機，其中驅動轉膛體實現規定往復間歇運動的機構稱為轉膛驅動機構，因此轉膛驅動機構是轉膛自動機的關鍵部位[1-2]。火炮要求其各個零件為全壽命件，轉膛驅動機構的性能和可靠性直接影響著轉膛自動機的使用性能。某新型轉膛自動機由驅動滑板與換向器共同組成的曲線槽帶動轉膛體回轉運動，由此實現該自動機的循環往復動作，完成射擊循環動作。在某新型轉膛炮射擊試驗中，發現該新型轉膛自動機在一定擊發次數之后，換向器的磨損較為嚴重，甚至產生裂紋，嚴重影響了該轉膛自動機的工作性能。

關于轉膛自動機驅動機構的研究，前人研究的重點多在于對驅動滑板曲線槽的優化設計上。文獻[3]運用五次多項式運動規律對滑板曲線槽進行設計，對提供轉膛體運動的穩定性有明顯作用。文獻[4]以某轉膛自動機為對象，建立了該自動機的數學模型，分析了不同滑板曲線槽的組合對轉膛體轉動穩定性的影響。文獻[1,5]基于相關工程經驗，給出了一些不同曲線方程的曲線槽設計方法，為設計轉膛驅動機構提供了一定的參考。綜上所述，轉膛炮的驅動機構一直是研究的重點，但是目前多數研究是針對驅動滑板的曲線槽，未對相關結構進行疲勞和壽命分析。本文以驅動機構中的換向器為對象，應用相關軟件對其疲勞失效進行分析，初步估計換向器在正常工作載荷作用下的工作壽命，為后續轉膛自動機換向器相關結構的設計和優化提供了理論依據。

1 換向器原理及動力學分析

1.1 換向器原理

某新型轉膛自動機的驅動機構主要由轉膛滑板和換向器組成，換向器在轉膛滑板的帶動下沿炮口軸向往復運動。圖1為轉膛驅動機構的示意圖，換向器以P點為旋轉中心，在自動機后坐階段時換向器旋轉至圖1中的實線段①部分，此刻換向器的一邊與驅動滑板共同組成完整的曲線槽來實現后坐動作。在自動機復進階段，換向器旋轉至圖1中的實線段②部分，此刻換向器的另一邊與驅動滑板組成完整的曲線槽來實現復進動作。

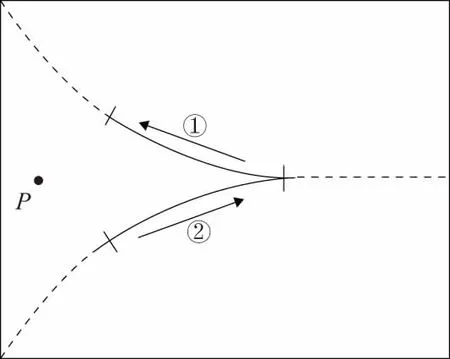
圖1 轉膛驅動機構示意圖

1.2 換向器載荷分析

換向器載荷分析計算是計算其疲勞壽命的基礎。因而在對換向器進行疲勞壽命分析之前，需要首先明確換向器在轉膛自動機工作循環中受到的載荷情況。在驅動滑板的帶動下，換向器在后坐與復進循環過程中單邊每次分別受到一次滾輪的接觸力。因此，換向器所受到的載荷為滾輪的循環載荷。圖2為換向器的三維模型，換向器和滾輪接觸的兩邊對稱，后坐時的接觸力大于復進時滾輪與換向器之間的接觸力[6]，故本文后續對換向器的疲勞壽命分析過程以后坐時為例。

圖2 換向器三維模型

為得到換向器的真實受力情況，考慮到在線測量時間長、成本高，而仿真技術速度快、精度高、成本低，因此最終決定采用動力學仿真的方法來獲得接觸力。采用動力學仿真軟件，首先需要建立轉膛自動機的運動模型，然后根據實際工況添加載荷，設置換向器和滾輪之間的接觸為光滑接觸，以二者之間的法向反力作為全反力。

火炮為典型的多剛體結構，滿足如下約束方程。以剛體i的質心在慣性系中的笛卡兒坐標和歐拉角為廣義坐標，即qi=[x,y,z,ξ,β,φ]T，(i=1,2,…,n)。應用拉格朗日待定乘子法，系統的動力學方程為

(1)

式中：M為廣義質量陣；q為系統廣義坐標陣；φq為約束方程的雅克比矩陣；Q*為廣義力列陣；λ為拉格朗日乘子。

為驗證動力學仿真的正確性，將試驗中實測的滑板速度和動力學仿真軟件得到的滑板速度進行對比。圖3為試驗所得滑板速度和仿真所得滑板速度的對比圖。由于接觸設置為光滑接觸，因此仿真速度的最大值相比于實測速度略大，且仿真后坐時間較短。

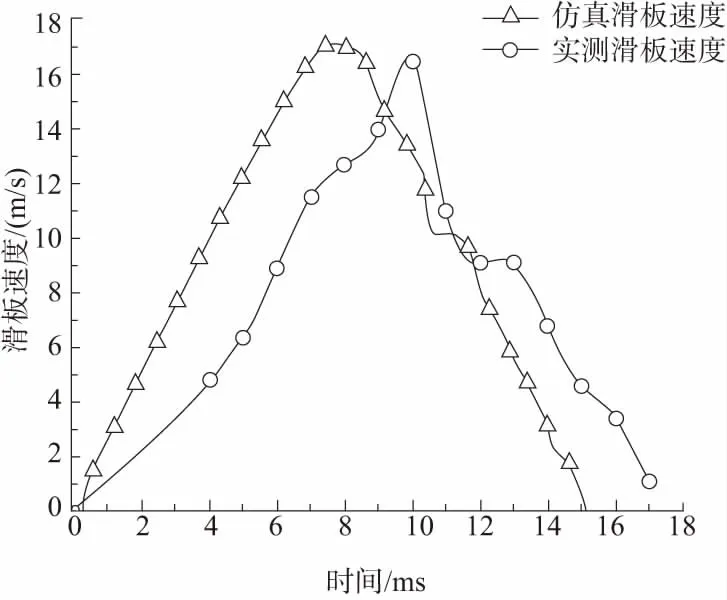
圖3 滑板速度對比

通過轉膛驅動滑板實測和仿真速度的對比可知，動力學仿真結果基本上符合實際工況，經過換向器的力源分析得知換向器在自動機工作循環中只有滾輪和換向器之間的接觸力，故可以以動力學仿真所獲得的載荷對換向器進行疲勞壽命分析。通過動力學仿真軟件計算可知滾輪與換向器之間的接觸力，換向器所受接觸力的最大值主要存在于趨近滑板曲線的拐點處。圖4為換向器與滾輪之間的接觸力，其中最大值為24840.65N。

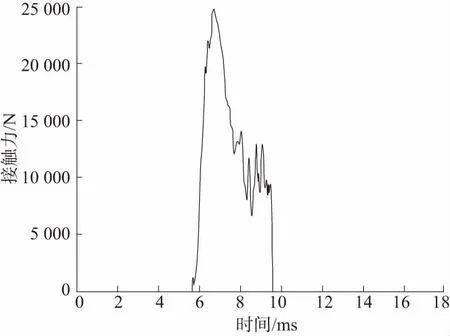
圖4 換向器與滾輪接觸力

2 換向器有限元仿真分析

2.1 有限元模型建立

根據換向器的幾何尺寸和相關參數，利用有限元軟件建立換向器的有限元模型，定義換向器的材料為某高強度合金鋼，其各項力學性能如表1所示[7]。根據換向器的實際工況設置邊界條件，采用網格自動劃分，設置網格大小為0.5mm，最終生成網格節點為481556，網格單元數量為337196，網格劃分效果如圖5所示。

表1 某高強度合金鋼的力學性能

圖5 換向器網格劃分示意圖

由動力學仿真軟件可知換向器主要受到的載荷為滾輪在轉膛自動機工作循環中的接觸反力，且接觸力只在滾輪進入換向器與驅動滑板共同組成的曲線槽內才存在。此時滾輪側面與換向器的側面相接觸，但是滾輪在運動時接觸力在變化，因此為方便施加載荷和計算，取滾輪與換向器之間接觸力最大時的狀態為靜止狀態，按照此刻換向器的真實受力和約束對換向器施加載荷并進行約束，如圖6所示。

圖6 換向器載荷施加及添加約束

2.2 換向器的有限元結果分析

對換向器施加載荷和添加約束后，利用有限元軟件對其進行計算。圖7為換向器在滾輪接觸力作用下的應力云圖。可以看出，換向器的應力分布在滾輪和換向器接觸處以及換向器曲線槽的根部，其中應力集中在換向器與滾輪相接觸的區域。因此可以判斷，該區域為換向器在載荷作用下最易失效的位置，其應力最大值為σs=1 569.5MPa，小于換向器材料的屈服強度σs=1 620MPa。

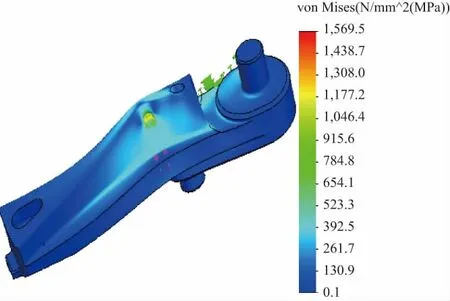
圖7 換向器應力云圖

雖然在自動機正常工況下，換向器的最大應力小于屈服強度極限，換向器可以正常工作，但該值與屈服強度值比較接近。轉膛自動機每擊發一次，換向器單邊與滾輪接觸一次，在此過程中換向器經歷的變化為從小到大，從大到小的載荷。因而在多次擊發的過程中，換向器受到周期性變化的應力，即交變應力，換向器在此狀態下長時間工作極易產生疲勞失效，因此需要對該換向器的應力集中部位進行疲勞分析和壽命分析，以防止因疲勞失效而影響轉膛自動機的性能，導致停射等事故的發生。

3 換向器的疲勞壽命分析

3.1 S-N曲線

由有限元分析的結果可知，在轉膛自動機正常工況下，換向器極易產生疲勞失效，應采用應力疲勞分析理論分析換向器的疲勞壽命[8]。目前最常用的疲勞分析方式是采用S-N曲線進行疲勞分析，而其中最重要的是要獲取材料的S-N曲線。S-N曲線是指材料發生疲勞破壞時的循環次數Ni與材料所受交變循環應力Si關系的曲線，能直接反映材料的疲勞性能。該曲線通常是在標準試棒在最大對稱循環載荷下進行疲勞試驗獲得，獲得材料的S-N曲線的最好方法是做疲勞試驗，但在一些不能進行疲勞試驗來獲得S-N曲線的情況下，可以利用材料的相關參數擬合一條近似的S-N曲線[9]。

S-N曲線常用冪函數公式表示，即

σmN=C

(2)

式中：σ為應力幅；N為應力循環次數；m、C為材料常數。

根據上式結合換向器材料某高強度合金鋼的相關參數擬合出某高強度合金鋼的S-N曲線圖，如圖8所示。

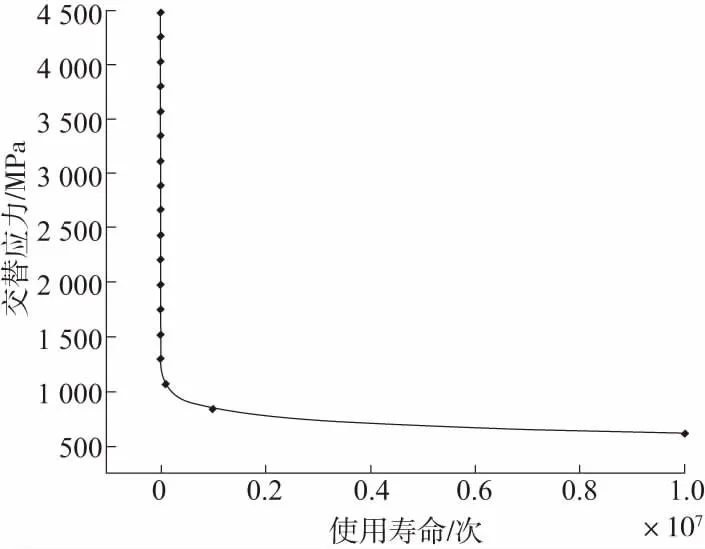
圖8 某高強度合金鋼的S-N曲線

3.2 疲勞壽命分析與試驗對比

疲勞破壞是指機械零部件在交變應力反復作用下，材料性能發生改變甚至出現斷裂的現象。機械零部件的疲勞破壞過程一般分為3個階段：疲勞裂紋生成階段、疲勞裂紋穩定擴展階段、疲勞裂紋不穩定擴展導致突然斷裂[10]。對換向器采用進行疲勞壽命分析的過程為：在對換向器靜態分析結果的基礎上，以應力和應力集中系數為參數，設置換向器材料的S-N曲線，根據Miner線性損傷累積規則進行計算，得出換向器的壽命。在對換向器進行疲勞分析時，將計算交變應力的手段設置為對等應力(von·Mises)，平均應力糾正選擇Soderberg，分析計算得到如圖9、圖10所示的疲勞數據。

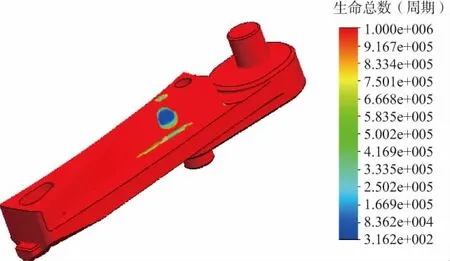
圖10 疲勞分析生命周期

從圖9中可以看出，換向器在經過一定次數載荷作用后，除了換向器和滾輪相接觸處，其余部分的損壞百分比均<1，圖9中換向器的深色區域為換向器的薄弱區域，即換向器與滾輪接觸處，說明此處應力較為集中，容易發生疲勞裂紋和破壞。

圖9 疲勞分析損壞百分比圖

從圖10可知，換向器各個部位的最低疲勞次數大概為316次，壽命較低的區域集中在換向器與滾輪接觸處，且區域較小，表示換向器在轉膛自動機正常工作316次后，換向器將會產生疲勞裂紋。

某新型轉膛自動機在經過500發左右擊發后，換向器出現了裂紋，如圖11所示。其余位置在試驗過程中未發生疲勞破壞，計算結果和試驗結果在數量級上較為接近，說明文中采用的疲勞壽命分析方法具有較高的工程實用價值。

圖11 試驗疲勞損壞

4 結語

在對某新型轉膛自動機進行動力學分析的基礎上，通過有限元方法分析得出換向器在正常工況下的應力分布，發現換向器在一定次數工作循環后易產生疲勞失效。在對正常工作循環下的換向器進行疲勞分析，得出換向器損壞的大概位置，并估算出其工作壽命為擊發316發彈，與試驗結果量級相一致。本文上述分析為換向器后續的改進設計和工藝提供了參考。