模糊控制在壓鑄機壓射速度控制系統中的應用

孔令成，陳若愚

(南京理工大學 機械工程學院，江蘇 南京 210094)

0 引言

壓力鑄造是將熔融狀態的金屬在高壓、高速的狀態下填充到型腔里，并繼續施加壓力，在壓力作用下凝固形成鑄件的一種精準、高效的有色合金精密成型技術。隨著壓鑄機性能的改進，能夠鑄造出各種復雜幾何結構的產品，壓鑄機越來越廣泛地應用在各個行業的各種裝備和零部件的制造中[1]。特別是近幾年新能源汽車的迅速發展對汽車輕量化提出了更高、更迫切的要求。目前汽車輕量化的主要方法是使用輕質材料，但汽車一些關鍵部件不能只依靠輕質材料，還需要合適的先進成型工藝予以支撐，壓鑄是汽車安全件、結構件實現高性能和輕量化的主要途徑。

1 壓鑄機速度控制系統物理模型

壓射機構是壓鑄機的關鍵部件，壓射機構的性能直接決定了壓鑄產品的質量。壓鑄機構包括壓射沖頭、壓射油缸、增壓和快壓射蓄能器、壓射桿以及壓射室等[2]。本文分析的是速度控制系統，增壓蓄能器不參與工作，所以速度控制系統可以簡化，以便于建模和分析[3]。

壓鑄機的壓射過程分為慢壓射和快壓射兩個階段，慢壓射是沖頭以較慢的速度推進，防止鑄件出現卷氣缺陷，沖頭經過澆料口以后進入快壓射部分，快壓射時沖頭以很高的速度推動金屬液填充至型腔內[4-5]。最難也是最重要的是對第二階段快壓射的控制。快壓射時的流量主要都是由蓄能器所提供，為了簡化模型，將蓄能器作為油源，簡化后的模型如圖1所示。

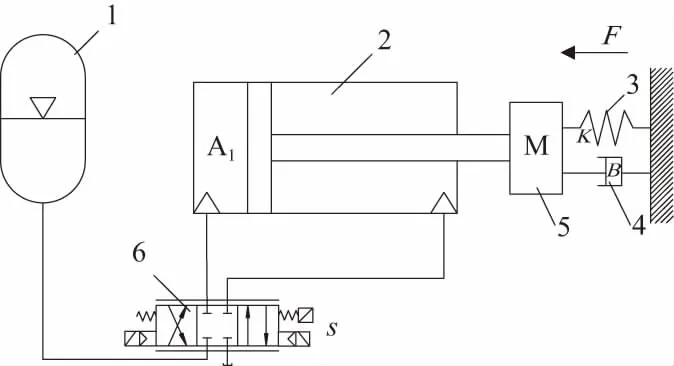
1—蓄能器；2—壓射油缸；3—彈簧振子；4—阻尼；5—負載；6—比例閥。

簡化的物理模型中的壓射油缸由于只有A1腔有高壓油的作用，因此將其簡化成簡單的非對稱油缸，將負載簡化成一個帶阻尼的彈簧[6]。比例閥是個帶有先導級的三級流量閥，通過電信號進行流量的控制，從而調節液壓桿的運動速度。

2 壓鑄機速度控制系統數學模型

2.1 蓄能器的數學模型

本文蓄能器選用的是氣囊式活塞蓄能器，蓄能器由于釋放的速度很快，所以可以看做絕熱過程，即滿足：

PVγ=const

(1)

假設蓄能器中的氣壓和液壓的壓力相同，可得

(2)

式中：V為蓄能器打開后任意時刻的空氣容積，m3；V0為蓄能器初始時刻的空氣容積，m3；P為蓄能器內任意時刻的壓力，Pa；P0為蓄能器預充氣壓力，Pa；γ絕熱指數，蓄能器釋放快時取1.4。

為了簡化數學模型，忽略蓄能器、進油腔和管路的油液壓縮性：

(3)

式中：Q為蓄能器的流量，m3/s；假設蓄能器至油缸之間的壓力損失為ΔPL，則有：

ΔPL=cQ2

(4)

P1=P-ΔPL

(5)

式中：ΔPL為蓄能器至進油腔油液的壓力損失，Pa；P1為壓射油缸的進油腔壓力，Pa；C為壓力損失系數，Pa·s2/m6。

由于蓄能器中減少的油液體積等于進入油缸進油腔的體積，可得：

(6)

V=V0+A1xp

(7)

從而可得

(8)

2.2 比例流量閥的數學模型

根據比例閥產品說明書可知，當△P=1.0MPa時額定流量為1500L/min，響應時間是10ms。此閥壓差與流量為

(9)

式中：ΔP實際為伺服比例閥進出口壓差，MPa；ΔP額定為伺服比例閥進出口額定壓差，MPa；Q額定為額定流量，m3/s；Q實際為實際流量，m3/s。

Q額定與輸入電流成正比:

Q額定=Ksvi

(10)

式中：i為電流，A；Ksv為流量增益，m3/(A·s)。

從而有

(11)

2.3 壓射油缸的數學模型

若不計泄漏，油腔的流量方程為

(12)

式中：V2為壓射油缸出油腔的體積與出油口到節流閥閥口之間的油液體積之和，m3；E為油液的有效體積彈性模量，Pa；A2為壓射油缸出油腔的油液作用面積，m2；xp為活塞桿的運動位移，m；P2為油缸出油腔內油液壓力，Pa；Q2為油缸的出油腔流量，m3/s。

V2=V′0-A2xp

(13)

式中：V′0為初始狀態下的出油腔體積與出油口到節流閥閥口之間的油液體積之和，m3。

壓射缸沖頭所受力的平衡方程為

(14)

式中：∑F為總的負載力，N；M為活塞和油液及負載的等效質量，kg；K為等效彈簧剛度，N·m-1；Fl為負載力，N；Fc為庫侖力，N；A1為壓射油缸進油腔的油液作用面積，m2；B為等效黏性阻尼系數，Ns·m-1。

由式(11)、式(12)可得到以下關系

(15)

由式(8)、式(13)、式(14)、式(15)得

(16)

3 模糊PID控制在壓射速度控制上的應用

3.1 模糊PID控制方案

PID控制具有可靠度高、穩定性好、簡單等特點，在工業控制領域應用廣泛，但由于壓鑄機速度控制系統是一種大滯后且非線性的復雜系統，因此固定的PID參數很難滿足壓鑄機的控制要求[7-8]。為了簡化數學模型，忽略蓄能器、進油腔和管路的油液壓縮性，但這樣得到的不是精確的數學模型，只是一定程度反映系統的實際情況。模糊控制不需要很精確的模型，且適用性好、魯棒性強。所以把二者結合得到的模糊PID同時擁有二者的優點，因此可以獲得更好的控制效果[9]，模糊PID控制系統原理如圖2所示。

圖2 模糊PID控制系統原理

模糊PID控制系統的執行過程是，先找出PID控制器的3個參數KP、KI、KD與速度偏差e和速度變化率ec之間的模糊關系，在工作過程中持續測量速度偏差和速度變化率，根據模糊推理對PID控制器的KP、KI、KD進行實時修正，使系統達到良好的性能。

3.2 模糊規則設計

模糊PID控制器有兩個輸入，分別是速度偏差e和速度變化率ec，輸出為利用模糊規則修改過的PID參數即ΔKP、ΔKI、ΔKD。定義e和ec論域為[-6，6]、[-3，3]；ΔKP、ΔKi、ΔKD的論域為[-1，1]、[-3，3]、[-0.2，0.2]；模糊集取為{NB，NM，NS，ZO，PS，PM，PB}。隸屬度函數選取最常用的三角型隸屬度函數如圖3所示，以Mamdani模糊系統為推理方法，如圖4所示，控制規則輸入和輸出之間的關系通過49個模糊規則用“If…and…then…”來表達。

圖3 隸屬度函數

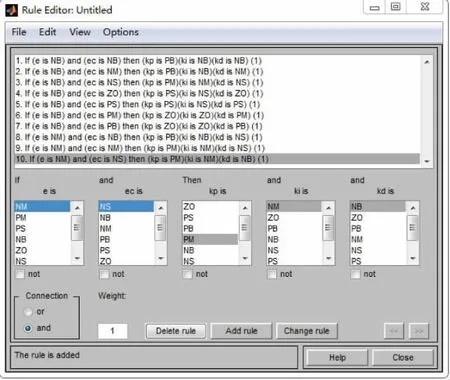
圖4 模糊規則(部分)

4 建模及仿真分析

在MATLAB/Simulink平臺上建立模糊控制壓射控制系統仿真模型(圖5)，系統的仿真參數見表1。圖5所示中的“speed” 是封裝了速度控制模型的自定義S-Function模塊，輸入信號幅值為12的階躍信號。

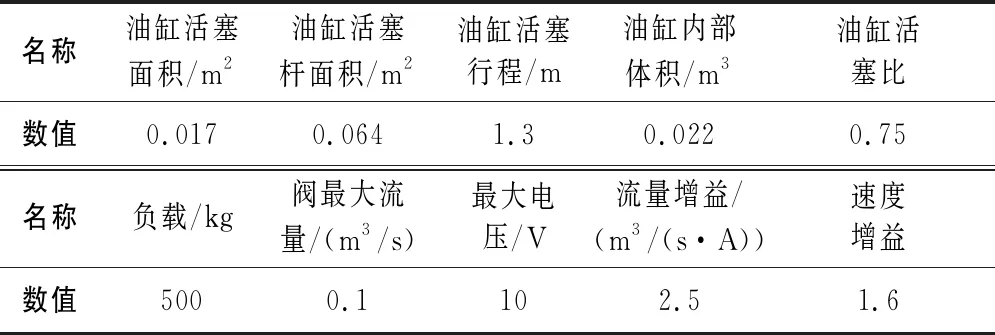
表1 速度控制系統的仿真參數

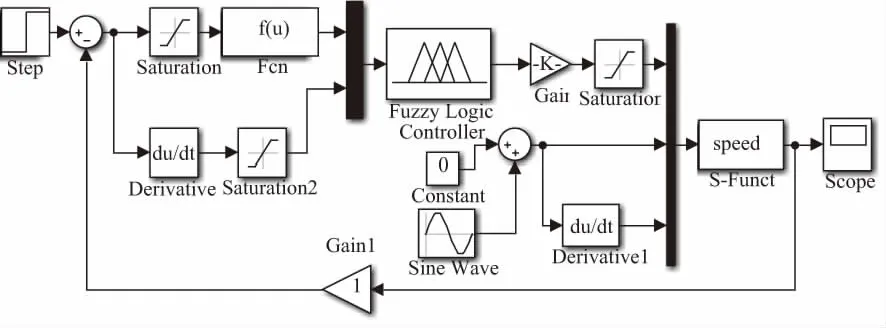
圖5 壓射速度模糊PID控制仿真模型

在MATLAB/Simulink中所得到的模糊PID和常規PID的結果如圖6所示。圖中Fuzzy PID是模糊PID控制下的曲線，曲線PID是常規PID控制下的曲線(KP=30、KI=15、KD=0.3)。在常規PID和模糊PID控制中穩定速度的時間分別維持在0.4s和0.6s左右。從圖中可以看出模糊PID得到的速度曲線比常規PID得到的速度曲線達到穩態速度所需要的時間更短，并且可以看出超調量幾乎為0，速度波動較小。

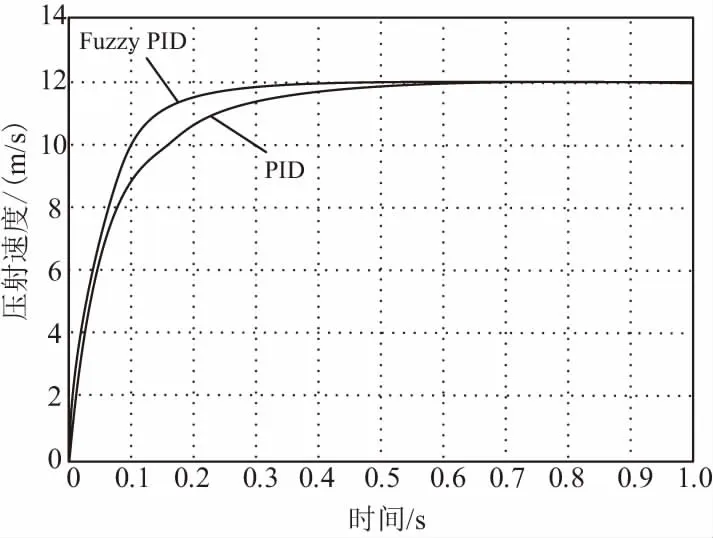
圖6 模糊PID與常規PID仿真結果

5 結語

綜上所述，本文首先建立了壓鑄機速度控制系統的物理模型，在物理模型的基礎上建立了速度控制系統的數學模型，設計了該系統的模糊控制器并在Simulink中進行仿真，其表現出的穩定性、速度響應特性等特點，比常規的PID控制更優秀，控制系統的穩定性和靈活性較高，可針對不同的控制對象對模糊控制、PID參數進行對應的修改，滿足壓鑄機的控制要求。