動生感應中的“單桿”專題評析

重慶 張大洪

單導體棒在磁場中切割磁感線運動而產生的動生感應電動勢中的過程與收尾問題，是一種重要的電磁感應問題；在動生感應中導體棒切割磁感線運動而產生感應電流，并同時受到安培力的作用，由于導體棒的速度變化導致安培力變化，因而導體棒運動過程中的加速度將發生相應變化；當導體棒加速度變為0后其必將做勻速直線運動，我們將其此時的速度稱作“收尾速度”；當在一定條件下，導體棒最終將做勻變速直線運動，我們將其不變的加速度稱作“收尾加速度”；下面我們從實例來分類討論此專題中的“收尾速度”與“收尾加速度”的分析方法。

一、“單桿”的收尾速度與動態過程的評析

【例1】(基本題型)如圖1-1所示，寬L=1 m的U形光滑導線框架與水平面成夾角θ=30°傾斜放置在與框面垂直向上的勻強磁場中，磁感應強度B=0.2 T；在框架上垂直框邊放一根質量m=0.8 kg，電阻r=0.08 Ω的導體棒ab；圖中定值電阻R=0.02 Ω，導體框架的電阻不計。現將ab棒從靜止釋放讓它沿框架無摩擦下滑，設框架足夠長且取g=10 m/s2。求ab棒運動的最大速度vm=？

圖1-1

圖1-2

【拓展一】將磁場方向改成豎直向上，且ab棒與框架間的動摩擦因數為μ=0.2，則ab棒的最后運動速度大小又為多少？

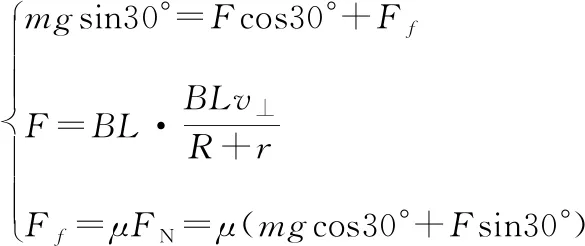
圖1-3

【點評】在計算感應電動勢時注意B、L、v必須兩兩正交時才能用E=BLv，否則要對B或v進行分解處理；在作安培力的方向時注意F⊥B、F⊥I。

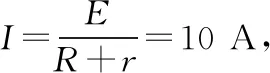
【拓展三】用功能原理處理棒的運動過程與最終狀態。在“拓展一”的條件中當ab棒的速度從v=1 m/s加速到v2=5 m/s的過程中，電阻R放出的焦耳熱為0.5 J，框架與棒由于摩擦而增加的內能為2 J，求棒在框架上滑動的距離為多少？

【分析】由于導體棒的重力提供其沿框面運動的動力，故該動力所做的功一部分用來增加棒的動能、一部分用來克服滑動摩擦力做功、一部分用來克服安培力做功；所以電磁感應的功能原理可以表述為W外動=ΔEk+W克安+W克摩+W克其他：其中

1.W外動表示棒所受到的使其相對于磁場運動的外動力對棒所做的功；

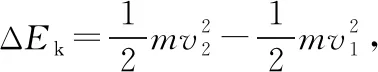
4.W克摩表示棒運動中克服摩擦力做的功，摩擦力為恒力時W克摩=Ffs；

5.W克其他表示棒運動中克服除摩擦阻力、安培阻力外的其他阻力所做的功。

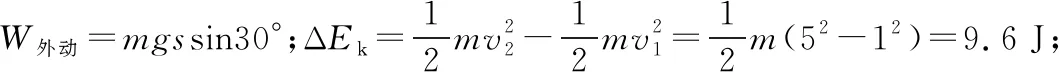
【拓展四】用平均力處理動態過程中的相關問題：在“(基本題型)”中當棒從靜止釋放沿框面下滑的高度為2 m時棒的速度增加為5 m/s，則此過程經歷了多少時間？

【拓展五】含電源的動生感應問題：在“(基本題型)”中若只將外電阻R換成一個電動勢為ε=2 V、內阻r=0.02 Ω的電池，題目中其他條件不變，如圖1-4所示；求棒由靜止釋放后所能達到的最大速度？

圖1-4

點評：注意感應電動勢與電池電動勢的方向關系及計算中的正、負關系。

【拓展六】含電容器的動生感應問題：在“(基本題型)”中若只將外電阻R換成一個C=5F的電容器，如圖1-5所示，題目中其他條件不變，求棒從靜止釋放沿框面下滑 8 m 時的速度及所經歷的時間？

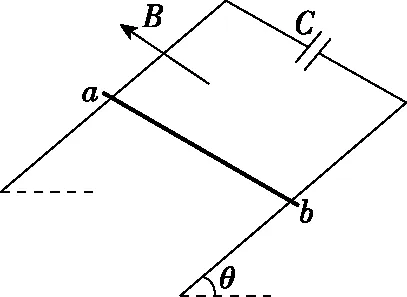
圖1-5

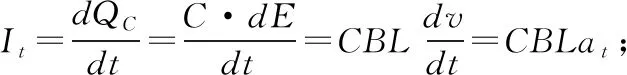
【拓展七】導體棒的恒定功率拉動問題：在“(基本題型)”中若給導體棒ab作用一個沿框面向上的外力使棒沿框面向上運動，運動中保證外力的功率不變，結果測出ab棒最后以速度20 m/s勻速運動；已知棒從靜止開始經過時間1.2 s沿框面運動s=10 m時的速度為10 m/s，求該過程中電路產生的焦耳熱。

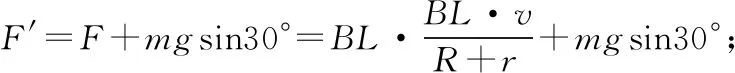
圖1-6

二、“單桿”的收尾加速度及過程評析

1.由電容器的充電來維持的勻加速收尾過程

【例2】如圖2-1所示，寬L=1 m的U形光滑導線框架與水平面成θ=30°角傾斜放置在豎直向上的勻強磁場中，磁感應強度B=0.2 T；在框架上垂直框邊放一根質量m=0.8 kg，電阻r=0.08 Ω的導體棒ab；圖中一個C=5 F的電容器連接在框架上，導體框架的電阻不計。現將ab棒從靜止釋放讓它沿框架無摩擦下滑，設框架足夠長且取g=10 m/s2。求：

圖2-1

(1)棒從靜止釋放后將做何種運動，最終的加速度是多少？

(2)棒從靜止釋放沿框面下滑9.854 m時的速度及所經歷的時間？

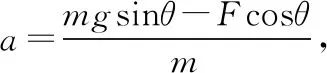
圖2-2

2.由電阻的相應變化來維持的勻加速收尾過程

【例3】圖2-3中AB、CD是兩根特制的完全相同的電阻絲，豎直固定在地面上，上端用電阻不計的導線連接，兩電阻絲間距為L，有一根質量為m電阻不計的金屬棒ab跨在AC兩點間的x軸原點處，并與電阻絲接觸良好且無摩擦，空間有垂直紙面向里的勻強磁場B，釋放金屬棒后它將向下滑動。求：

圖2-3

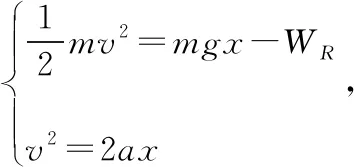
3.由外力的變化維持的勻變速收尾過程

【例4】圖2-4中兩相互平行的光滑金屬導軌位于水平面內，間距L=0.2 m，在導軌的一端接有阻值為R=0.5 Ω的電阻；在x≥0區域有一與水平面垂直的均勻磁場B=0.5 T；一質量為m=0.1 kg的金屬桿垂直放置在導軌上并以v0=2 m/s的初速度進入磁場中，在安培力及垂直于桿的水平外力F共同作用下做勻變速直線運動，加速度大小為a=2 m/s2方向與初速度方向相反；設導軌及金屬桿的電阻均不計且接觸良好，求：

圖2-4

(1)電流為0時金屬桿所處的位置？

(2)電流為最大值的一半時施加在金屬桿上外力F的大小及方向？

(3)保持其他條件不變而初速度v0取不同值，則開始時外力F的方向與初速度v0取值的關系？

【分析】由題意知，桿必向右做勻減速直線運動到速度為0后再向左做勻加速直線運動直到離開磁場區域，故電流為0時表示桿的速度為0；

①若此時桿向右運動，則外力方向不定，我們假設外力F水平向右由牛頓定律有F安-F=ma即F=F安-ma=BIL-ma=-0.18 N，故桿向右運動，外力F大小為0.18 N，方向水平向左。②若此時桿向左運動，則外力F方向必水平向左且有F-F安=ma即F-BLI=ma代入數據得F=0.22 N。