多決策覆蓋信息系統(tǒng)的約簡(jiǎn)

許麗婷 李進(jìn)金? 林藝東 李怡靚

(1-閩南師范大學(xué)數(shù)學(xué)與統(tǒng)計(jì)學(xué)院，漳州 3 63000;2-福建省粒計(jì)算及其應(yīng)用重點(diǎn)實(shí)驗(yàn)室，漳州 3 63000)

1 引言

粗糙集理論[1-3]作為一種處理不精確、不一致、不完整等各類不完備信息的有效工具，由波蘭科學(xué)家Pawlak在1982年創(chuàng)立.粗糙集理論是一種天然的數(shù)據(jù)挖掘或者知識(shí)發(fā)現(xiàn)方法，它與概率論[4]、模糊理論[5]、證據(jù)理論[6-8]等領(lǐng)域都有相關(guān)的結(jié)合.

覆蓋粗糙集理論為經(jīng)典粗糙集的一種推廣，其約簡(jiǎn)理論一直受到廣泛的關(guān)注.Zhu[9]對(duì)覆蓋提出了一種約簡(jiǎn)方法，該約簡(jiǎn)是產(chǎn)生相同覆蓋上、下近似的最小覆蓋，為數(shù)據(jù)挖掘中消除冗余提供了一種有效技術(shù).覆蓋信息系統(tǒng)可以進(jìn)一步的推廣到覆蓋決策信息系統(tǒng)，其中用劃分刻畫決策屬性的覆蓋決策信息系統(tǒng)的約簡(jiǎn)理論的研究十分廣泛.夏秀云等[10]利用信息熵，討論協(xié)調(diào)覆蓋決策系統(tǒng)的相關(guān)約簡(jiǎn).辨識(shí)矩陣是覆蓋決策信息系統(tǒng)約簡(jiǎn)理論的一個(gè)重要的工具.Chen等[11]在決策為劃分的覆蓋決策信息系統(tǒng)中提出了一種減少覆蓋決策系統(tǒng)屬性的方法.由于決策為劃分有一定的局限性，因此一些學(xué)者將決策從劃分推廣為覆蓋，然后再對(duì)覆蓋決策信息系統(tǒng)的約簡(jiǎn)理論進(jìn)行研究.張燕蘭和李進(jìn)金[12]在文獻(xiàn)[11]的基礎(chǔ)上研究了在決策為覆蓋的覆蓋決策信息系統(tǒng)中保持正域不變的相對(duì)約簡(jiǎn)，并通過構(gòu)造辨識(shí)矩陣求其約簡(jiǎn).Zhang和Li[13]介紹了一族覆蓋的兩種相對(duì)約簡(jiǎn)，并且通過構(gòu)造了兩個(gè)辨識(shí)矩陣研究所有相對(duì)約簡(jiǎn)的結(jié)構(gòu).然而在根據(jù)辨識(shí)矩陣求其約簡(jiǎn)的過程中，由于辨識(shí)矩陣過于復(fù)雜，而導(dǎo)致計(jì)算過程中時(shí)間復(fù)雜度為指數(shù)級(jí).在數(shù)據(jù)集相對(duì)較大時(shí)難以計(jì)算.本文通過將決策為覆蓋的覆蓋決策信息系統(tǒng)轉(zhuǎn)化為多決策覆蓋信息系統(tǒng)，提出了兩類新約簡(jiǎn)，并將此系統(tǒng)下的兩類約簡(jiǎn)與文獻(xiàn)[13]下的約簡(jiǎn)方法進(jìn)行比較.

本文通過特征函數(shù)將覆蓋決策信息系統(tǒng)轉(zhuǎn)化為多決策覆蓋信息系統(tǒng).首先，在多決策覆蓋信息系統(tǒng)下定義了兩類協(xié)調(diào)集，構(gòu)造了兩個(gè)辨識(shí)矩陣，通過這兩個(gè)辨識(shí)矩陣研究多決策覆蓋信息系統(tǒng)的約簡(jiǎn)問題，討論多決策覆蓋信息系統(tǒng)中的兩類協(xié)調(diào)集與覆蓋決策信息系統(tǒng)中的上近似協(xié)調(diào)集之間的聯(lián)系.

2 預(yù)備知識(shí)

在采集數(shù)據(jù)的過程中，可能由于條件不夠等原因使得一些對(duì)象的決策缺失或者不能完全確定，這時(shí)若將決策刻畫為劃分，則會(huì)導(dǎo)致數(shù)據(jù)部分失真，故在一些決策信息系統(tǒng)中的決策屬性以覆蓋刻畫更恰當(dāng)，下面將給出例子進(jìn)行解釋說明.

例1 若某企業(yè)想要判斷每項(xiàng)技術(shù)的成熟性，為了對(duì)技術(shù)進(jìn)行創(chuàng)新決策.設(shè)決策信息系統(tǒng)為(U,A,F,d)，U表示每項(xiàng)技術(shù)的集合，共有5項(xiàng)技術(shù)待評(píng)估.A={a1,a2}表示影響各項(xiàng)技術(shù)成熟程度的屬性，a1表示市場(chǎng)需求的情況，a2表示需求變化的情況.F={f1:U→Vl(al∈A)}為每項(xiàng)技術(shù)和各個(gè)屬性的關(guān)系，即每項(xiàng)技術(shù)在各個(gè)屬性下的取值，Vl為屬性al的值域.d:U→Vd表示技術(shù)的成熟程度，Vd為屬性d的值域.如表1所示，有一個(gè)連續(xù)值決策信息系統(tǒng)，其條件屬性和決策屬性的取值范圍在[0,4]內(nèi).

表1 例1中的決策信息系統(tǒng)

對(duì)任意B?A,d，定義RB,Rd如下

其中εal>0,εd>0，顯然RB,Rd滿足自反、對(duì)稱，但一般不滿足傳遞.因此

Ci={(Rai)s(x)|x∈U},i=1,2,Cd={(Rd)s(x)|x∈U}

為覆蓋.

若εa1=0.4,εa2=0.2,εd=1.2，則可得到三個(gè)覆蓋為

C1={{x1,x2,x6},{x1,x2},{x3,x5},{x1,x4}},

C2={{x1,x2,x5},{x1,x2,x3,x5},{x3,x4,x5},{x3,x4},{x2,x3,x5}},

Cd={{x1,x2,x3,x5},{x1,x2,x3,x4},{x1,x3,x5},{x2,x4}}.

例2 如表2所示，給出了一個(gè)不完備決策信息系統(tǒng)I=(U,A,F,d)，其中對(duì)象集為U，屬性集為A，F(xiàn)={f1:U→Vl(al∈A)}代表對(duì)象和屬性的關(guān)系集，Vl為屬性al的值域，d:U→Vd，其中Vd取有限值.

表2 例2中的不完備決策信息系統(tǒng)

對(duì)于B?A，定義如下優(yōu)勢(shì)關(guān)系

設(shè)I=(U,A,F,d)為不完備決策信息系統(tǒng)，對(duì)于決策d,U可以被劃分為有序的類

D={Dt,t∈T},T={1,2,···,k}.

對(duì)于任意r,s∈T，若r>s，則代表Dr中的元素優(yōu)于Ds中的元素，因此，這些有序的決策類可以分別使用向上聯(lián)合和向下聯(lián)合近似來表示，有

由表2可得

決策類為D={D1,D2}，其中D1={x2,x5},D2={x1,x3,x4}.由于2>1，因此D2中的對(duì)象比D1中的對(duì)象優(yōu)，根據(jù)向上聯(lián)合近似的定義可以得到

例1和例2表明在一些決策信息系統(tǒng)中，利用覆蓋刻畫其條件屬性與決策屬性更具有合理性，故研究以覆蓋刻畫其決策的覆蓋決策信息系統(tǒng)的屬性約簡(jiǎn)問題具有理論與實(shí)踐意義.以下給出了覆蓋決策信息系統(tǒng)的相關(guān)知識(shí)，其決策以覆蓋刻畫.

定義1[11]設(shè)A={Cj|j=1,2,···,n}為U上的一族覆蓋，對(duì)任意x∈U，則x在覆蓋A下的鄰域定義為

(x)A=∩{K|x∈K,K∈Cj,j=1,2,···,n}.

A誘導(dǎo)的U上的一個(gè)覆蓋為

cov(A)={(x)A|x∈U}.

對(duì)任意B?A,x,y∈U，有如下性質(zhì)：

1)y∈(x)B?(y)B?(x)B；

2) (x)B=∩C∈B(x)C；

3) (x)A?(x)B,(x)B=(x)cov(B).

根據(jù)定義1，可得一對(duì)關(guān)于覆蓋cov(A)的近似算子.

定義2[9]設(shè)A={Cj|j=1,2,···,n}為U上的一族覆蓋，對(duì)任意X?U，X關(guān)于cov(A)的上近似算子定義為

易得它的對(duì)偶下近似算子為

Zhang和Li[13]給出了有關(guān)保持上下近似算子不變的約簡(jiǎn)理論以及辨識(shí)矩陣.

定義4[13]設(shè)(U,A,CD)是覆蓋決策信息系統(tǒng)，對(duì)x,y∈U且有Di∈CD，記

稱D(x,y)為x對(duì)y的上近似辨識(shí)集，則D={D(x,y)|x,y∈U}為x對(duì)y的上近似辨識(shí)矩陣.

引理1[13]設(shè)(U,A,CD)是覆蓋決策信息系統(tǒng)，B是A的上近似協(xié)調(diào)集，當(dāng)且僅當(dāng)D(x,y)?=?時(shí)，B∩D(x,y)?=?.

引理2[6]設(shè)C是A的上近似核心，且C∈A，當(dāng)且僅當(dāng)存在x,y∈U，使得D(x,y)={C}.

例3 設(shè)論域U={1,2,3,4,5}，U的一族覆蓋為A={C1,C2,C3}，CD為U的一個(gè)覆蓋，且

C1={{1,2,4},{2,3,5},{1,5}},C2={{1,3,4},{2,5},{4,5}},

C3={{1,4,5},{2,4},{3,5}},CD={{1,3},{2,4,5},{1,3,4},{2,5}}.

易得表3.

表3 例3中各點(diǎn)的鄰域

由表3可以得出

從而上近似辨識(shí)矩陣為

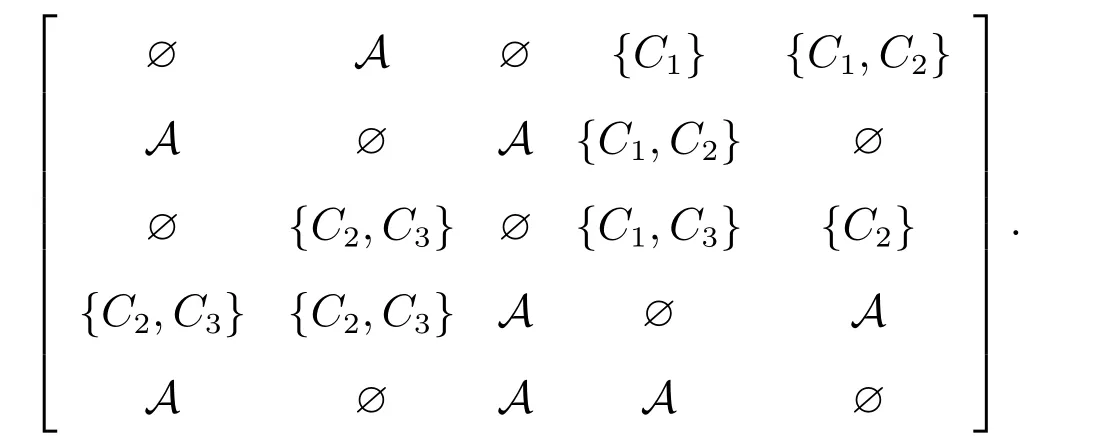
根據(jù)引理1知，B={C1,C2}是上近似協(xié)調(diào)集，但B1={C1}和B2={C2}都不是上近似協(xié)調(diào)集，所以B={C1,C2}是上近似約簡(jiǎn)集.

3 基于多決策覆蓋信息系統(tǒng)type-1辨識(shí)矩陣的約簡(jiǎn)

首先，給出特征函數(shù)的定義，而后通過特征函數(shù)將覆蓋決策信息系統(tǒng)中以覆蓋刻畫的決策轉(zhuǎn)化為一個(gè)形式背景，從而產(chǎn)生多決策覆蓋信息系統(tǒng).

定義5 設(shè)(U,A,CD)是覆蓋決策信息系統(tǒng)，CD={D1,D2,···,Dn}是U上的一個(gè)覆蓋，特征函數(shù)定義為

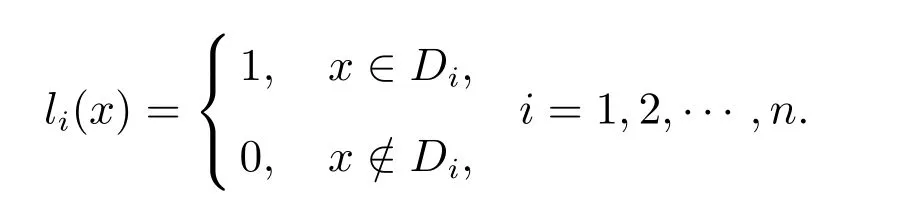
定義6 設(shè)(U,A,CD)是覆蓋決策信息系統(tǒng)，其中A為U上的一族覆蓋，CD={D1,D2,···,Dn}為U上的一個(gè)覆蓋，LD={l1,l2,···,ln}，其中l(wèi)i:U→{0,1},i=1,2,···,n，則稱(U,A,LD)為多決策覆蓋信息系統(tǒng).

對(duì)于多決策覆蓋信息系統(tǒng)定義一個(gè)U上的等價(jià)關(guān)系如下.

定義7 設(shè)(U,A,LD)是多決策覆蓋信息系，對(duì)x,y∈U，有

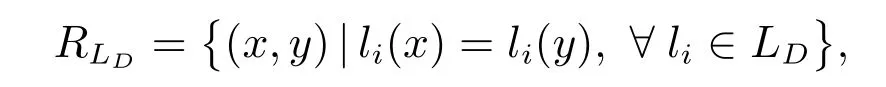
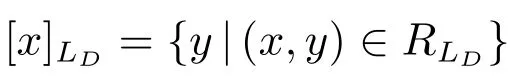
當(dāng)LD={li}時(shí)，有

下面給出關(guān)于多決策信息系統(tǒng)type-1覆蓋協(xié)調(diào)集和type-1覆蓋約簡(jiǎn)集的判定定理.

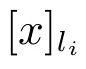
定理1 設(shè)(U,A,CD)是覆蓋決策信息系統(tǒng)，(U,A,LD)是多決策覆蓋信息系統(tǒng)，若B為覆蓋信息系統(tǒng)的上近似協(xié)調(diào)集，則B為多決策覆蓋信息系統(tǒng)的type-1覆蓋協(xié)調(diào)集.

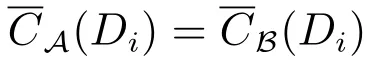
然而，反之不一定成立，下面舉例說明.

例4 設(shè)論域U={1,2,3,4,5}，U的一族覆蓋為A={C1,C2,C3}，CD為的一個(gè)覆蓋，且C1={{1,2},{2,3,4},{4,5}},C2={{1,2,3},{3,4},{5}},C3={{1,2},{3,4},{4,5}}.

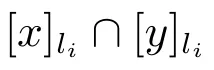
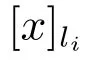
我們可以通過構(gòu)造辨識(shí)矩陣來描述覆蓋協(xié)調(diào)集和覆蓋約簡(jiǎn)集.首先，針對(duì)type-1覆蓋協(xié)調(diào)集和type-1覆蓋約簡(jiǎn)集構(gòu)造對(duì)應(yīng)的type-1多決策覆蓋辨識(shí)集并給出相關(guān)定理.

定義9 設(shè)(U,A,LD)是多決策覆蓋信息系統(tǒng)，對(duì)x,y∈U，存在li∈LD，記

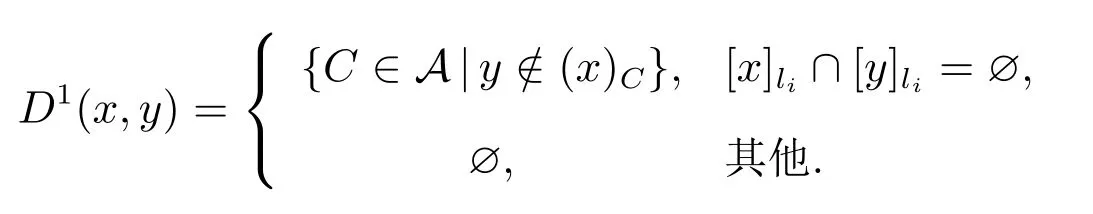
稱D1(x,y)為x對(duì)y的type-1多決策覆蓋辨識(shí)集，則D1={D1(x,y)|x,y∈U}為x對(duì)y的type-1多決策覆蓋辨識(shí)矩陣.

下面通過構(gòu)造的type-1多決策覆蓋辨識(shí)集和type-1多決策覆蓋辨識(shí)矩陣來判定type-1覆蓋協(xié)調(diào)集和type-1覆蓋約簡(jiǎn)集.

定理3 設(shè)(U,A,LD)是多決策覆蓋信息系統(tǒng)，B是type-1覆蓋協(xié)調(diào)集，當(dāng)且僅當(dāng)D1(x,y)?=?時(shí)，B∩D1(x,y)?=?.

例5 續(xù)例3，由覆蓋CD={{1,3},{2,4,5},{1,3,4},{2,5}}，可以得到如表4的一個(gè)形式背景.

表4 例5中x與li的關(guān)系

由表4可知產(chǎn)生的等價(jià)類為

從而可得一個(gè)type-1多決策覆蓋辨識(shí)矩陣

根據(jù)定理3知，B={C1,C2}是type-1覆蓋協(xié)調(diào)集，但B1={C1}和B2={C2}都不是type-1覆蓋協(xié)調(diào)集，所以B={C1,C2}是type-1覆蓋約簡(jiǎn)集.

對(duì)于例3，在多決策覆蓋信息系統(tǒng)下求出的約簡(jiǎn)與覆蓋決策信息系統(tǒng)的結(jié)果相同.在計(jì)算辨識(shí)矩陣的過程中，由于文獻(xiàn)[13]在計(jì)算辨識(shí)矩陣時(shí)需要計(jì)算的是上近似，而本文只需計(jì)算等價(jià)類，所以此方法比文獻(xiàn)[13]中的方法簡(jiǎn)便，且計(jì)算量小，節(jié)省時(shí)間.

在計(jì)算出type-1多決策覆蓋辨識(shí)矩陣之后，我們不僅可以通過定理3得出type-1覆蓋協(xié)調(diào)集和type-1覆蓋約簡(jiǎn)集，還可以通過以下區(qū)分函數(shù)來求得多決策覆蓋信息系統(tǒng)的約簡(jiǎn)集.

定義10 設(shè)(U,A,LD)是多決策覆蓋信息系統(tǒng)，D1={D1(x,y)|x,y∈U}為type-1多決策覆蓋辨識(shí)矩陣，記

M=∧{∨{C|C∈D1(x,y)}|x,y∈U},

M稱為覆蓋區(qū)分函數(shù)，其中∧表示(合取)運(yùn)算，∨表示(析取)運(yùn)算.

由定義10，可以得到如下定理.

定理4 設(shè)(U,A,LD)是多決策覆蓋信息系統(tǒng)，D1={D1(x,y)|x,y∈U}為type-1多決策覆蓋辨識(shí)矩陣，覆蓋區(qū)分函數(shù)M的最小析取范式是

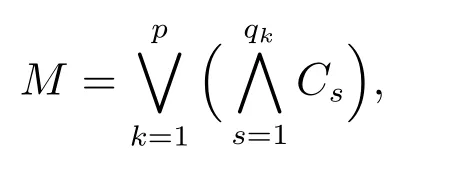
其中Bk={Cs|s=1,2,···,qk},{Bk|k=1,2,···,p}是type-1覆蓋約簡(jiǎn)集.

例6 續(xù)例5，利用區(qū)分函數(shù)有

M=C1∧(C2∨C3)∧(C1∨C3)∧(C1∨C2∨C3)∧(C1∨C2)∧C2=C1∧C2.

所以B={C1,C2}是type-1覆蓋約簡(jiǎn)集.

將多決策覆蓋信息系統(tǒng)中的覆蓋分類后，便于研究不同覆蓋各自的特征.下面給出覆蓋分類及判別方法.

定義11 設(shè)(U,A,LD)是多決策覆蓋信息系統(tǒng)，Bk(k≤r)為所有覆蓋約簡(jiǎn)集，記

Ci∈C時(shí)，稱Ci為核心覆蓋，C稱為核心覆蓋集；Ci∈K時(shí)，稱Ci為相對(duì)必要覆蓋，K稱為相對(duì)必要覆蓋集；Ci∈I時(shí)，稱Ci為不必要覆蓋，I稱為不必要覆蓋集.

定理5 設(shè)(U,A,LD)是多決策覆蓋信息系統(tǒng)，則下列命題等價(jià)：

1)C′是核心覆蓋；

2) 存在x,y∈U,D1(x,y)={C′}；

3) 若C′為不必要覆蓋?存在li∈LD，使得(x)(C′)?[x]li∪(x)C′.

4 基于多決策覆蓋信息系統(tǒng)type-2辨識(shí)矩陣的約簡(jiǎn)

下面給出另一類多決策覆蓋辨識(shí)矩陣來判定覆蓋協(xié)調(diào)集和覆蓋約簡(jiǎn)集.

由定理1上近似協(xié)調(diào)集是type-1覆蓋協(xié)調(diào)集可類似的推出上近似協(xié)調(diào)集是type-2覆蓋協(xié)調(diào)集.

定理8 設(shè)(U,A,CD)是覆蓋決策信息系統(tǒng)，(U,A,LD)是多決策覆蓋信息系統(tǒng)，若B為覆蓋信息系統(tǒng)的上近似協(xié)調(diào)集，則B為覆蓋信息系統(tǒng)(U,A,CD)的上近似協(xié)調(diào)集，當(dāng)且僅當(dāng)B為多決策覆蓋信息系統(tǒng)(U,A,LD)的type-2覆蓋協(xié)調(diào)集.

定理9 設(shè)(U,A,LD)多決策覆蓋信息系統(tǒng)，若B為type-2覆蓋協(xié)調(diào)集，則B為type-1覆蓋協(xié)調(diào)集.

反之，不一定成立，下面舉例說明.

類似定理2，可以得到如下定理，根據(jù)此定理構(gòu)造type-2多決策覆蓋辨識(shí)集.

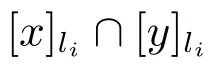
定義13 設(shè)(U,A,LD)是多決策覆蓋信息系統(tǒng)，對(duì)x,y∈U，任意li∈LD，記稱D2(x,y)為x對(duì)y的type-2多決策覆蓋辨識(shí)集，則D2={D2(x,y)|x,y∈U}為x對(duì)y的type-2多決策覆蓋辨識(shí)矩陣.

通過上述構(gòu)造的type-2多決策覆蓋辨識(shí)集和type-2多決策覆蓋辨識(shí)矩陣給出相關(guān)的type-2覆蓋協(xié)調(diào)集和type-2覆蓋約簡(jiǎn)集的定理.

根據(jù)定理3中type-1覆蓋協(xié)調(diào)集的充要條件，類似的可以得出type-2覆蓋協(xié)調(diào)集的充要條件.

定理11 設(shè)(U,A,LD)是多決策覆蓋信息系統(tǒng)，B是type-2覆蓋協(xié)調(diào)集，當(dāng)且僅當(dāng)D2(x,y)?=?時(shí)，B∩D2(x,y)?=?.

例8 由例5的等價(jià)類可得一個(gè)type-2多決策覆蓋辨識(shí)矩陣

根據(jù)定理11知B={C2}是type-2覆蓋約簡(jiǎn)集.

從例8可以看出，type-2多決策覆蓋辨識(shí)矩陣求出的約簡(jiǎn)集與type-1多決策覆蓋辨識(shí)矩陣有所不同.由于type-1多決策覆蓋辨識(shí)矩陣中的非空集合比type-2多決策辨識(shí)矩陣中的非空集合多，因此，在利用區(qū)分函數(shù)來計(jì)算約簡(jiǎn)集時(shí)tpye-2比type-1計(jì)算量小.

對(duì)于type-2多決策覆蓋辨識(shí)矩陣，也有類似于定義10的覆蓋區(qū)分函數(shù)

M=∧{∨{C|C∈D2(x,y)}|x,y∈U}.

在type-2多決策覆蓋辨識(shí)集下也有相關(guān)覆蓋分類的判別方法.

根據(jù)定理5，可以類似給出type-2多決策覆蓋辨識(shí)集下核心覆蓋的等價(jià)條件.

定理12 設(shè)(U,A,LD)是多決策覆蓋信息系統(tǒng)，則下列命題等價(jià)：

1)C′′是核心覆蓋；

2) 存在x,y∈U,D2(x,y)={C′′}；

由定理6，同理可以給出type-2多決策覆蓋辨識(shí)集下不必要覆蓋的等價(jià)條件.

結(jié)合定理12與定理13，得出相對(duì)必要覆蓋的充要條件.

定理14 設(shè)(U,A,LD)是多決策覆蓋信息系統(tǒng)，則有以下結(jié)論：

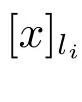
5 結(jié)束語

本文將覆蓋決策信息系統(tǒng)中以覆蓋刻畫的決策通過特征函數(shù)轉(zhuǎn)化為由0和1組成的形式背景，給出了多決策覆蓋信息系統(tǒng)的定義，進(jìn)而研究在多決策覆蓋信息系統(tǒng)下的約簡(jiǎn).在多決策覆蓋信息系統(tǒng)中提出兩類協(xié)調(diào)集判定方法，構(gòu)造了兩個(gè)相應(yīng)的辨識(shí)集，進(jìn)一步討論多決策覆蓋信息系統(tǒng)中的兩類協(xié)調(diào)集與覆蓋決策信息系統(tǒng)的協(xié)調(diào)集之間的關(guān)系.

對(duì)于本文給出的兩類多決策覆蓋辨識(shí)矩陣，計(jì)算量相對(duì)較小，可以節(jié)省求解覆蓋約簡(jiǎn)的時(shí)間，在實(shí)際應(yīng)用中具有一定的意義.此外，還可以繼續(xù)討論三個(gè)辨識(shí)矩陣之間的關(guān)系，以及三個(gè)辨識(shí)矩陣所產(chǎn)生的約簡(jiǎn)集之間的聯(lián)系.