Cahn-Hilliard方程的時間雙層網格有限元方法

王旦霞, 賈宏恩, 李亞倩

(太原理工大學數學學院，太原030024)

1 引言

Cahn-Hilliard方程是一個非常重要的數學物理模型，該方程是由Cahn和Hilliard在1958年提出，用于描述復雜的相分離和粗化現象[1-3].本文要研究的Cahn-Hilliard方程具有如下形式

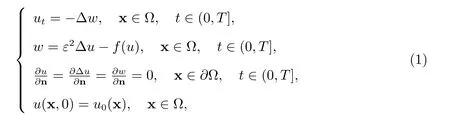
許多學者針對快速數值求解非線性問題進行了研究.例如，文獻[9]中研究了有限差分格式和自適應時間步長方法，文獻[10]提出了大時間步長方法，文獻[11]提出了兩層空間網格方法.最近，針對時間分數階水波模型，文獻[12]中提出了時間雙層網格有限元方法，文獻[13]中使用該方法快速求解空間分數階Allen-Cahn方程，并證明了該方法的有效性和可行性.

受文獻[12,13]的啟發，本文針對非線性Cahn-Hilliard方程，提出了時間雙層網格有限元方法，該方法需要分兩步進行：第一步，在粗的時間步長上求解非線性系統；第二步，在細的時間步長上求解線性系統.相比傳統的Galerkin有限元方法，在精確度相同的情況下，本文提出的方法可以節省計算時間.

2 理論準備

為了之后證明的方便，首先引入一些范數的定義和引理.L2(Ω)是平方可積函數空間，內積和范數分別是

H1(Ω)是通常的Sobolev空間，半范和范數分別是

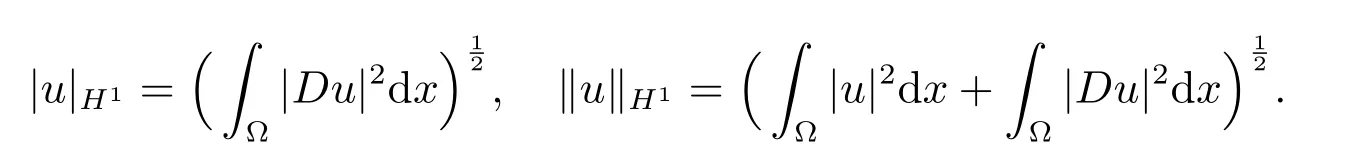
其中

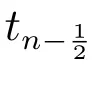
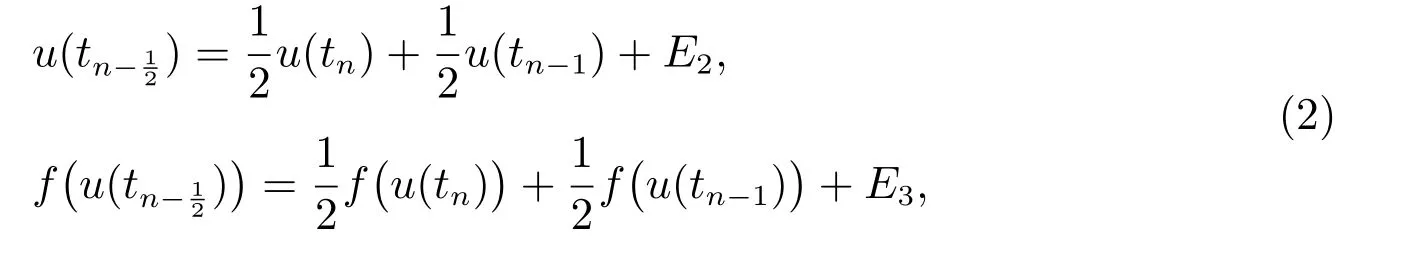
且

采用以下的記法

注1 引理1和引理2中的常數C獨立于時間t.

3 數值格式與TT-M FE方法

3.1 全離散格式

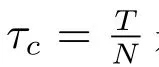
令Th={e}為Ω的擬一致剖分，hi是空間網格步長，且h=max0≤i≤n hi，對任意的整數k，定義有限元空間

其中Pk(x,y)是x,y的次數不超過k∈Z+的多項式的集合.問題(1)的的全離散格式為：求Un:[0,T]?→Vh，使得

其中U0=uh0(x)是u0(x)的一個逼近，Un代表u(x,t)的全離散逼近.

3.2 時間雙層網格有限元方法

步驟3 基于插值結果UmI，考慮時間細網格上線性系統，即求UmF:[0,T]?→Vh，

其中fu是f關于u的導數.

4 穩定性分析

定理1 對于時間粗網格系統(6)式，TT-M系統(7)式，下面的不等式成立

證明 分兩步完成：第一步，時間粗網格系統(6)式的等價形式為

先利用Cauchy-Schwarz不等式和Young不等式對(11)式左端第二項進行估計有

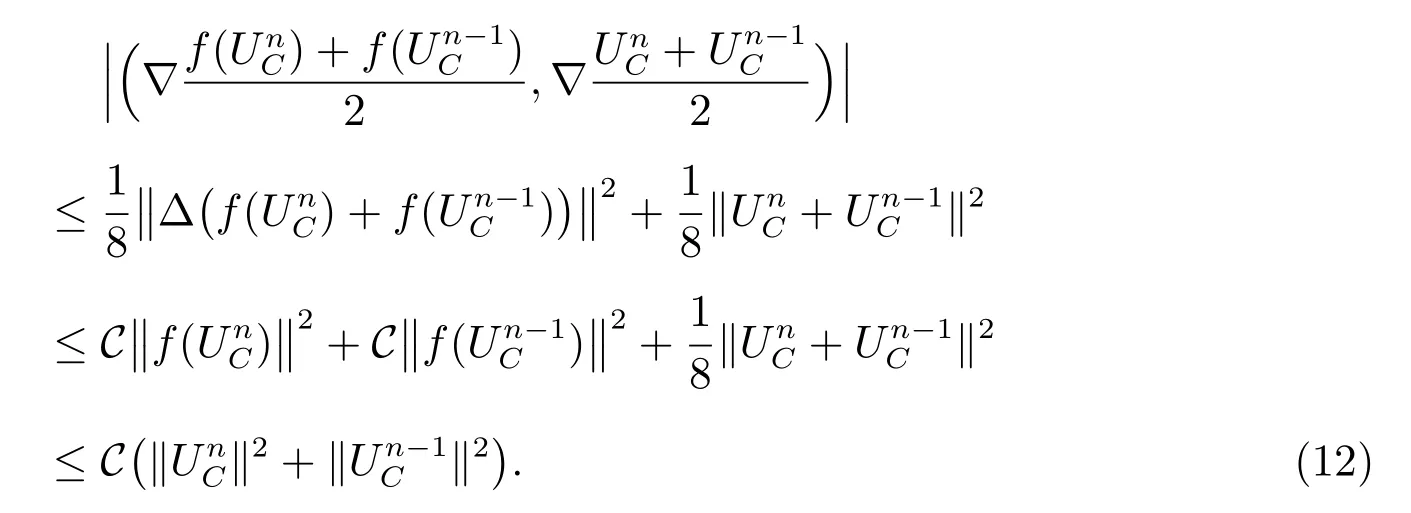
結合(11)式和(12)式，故有

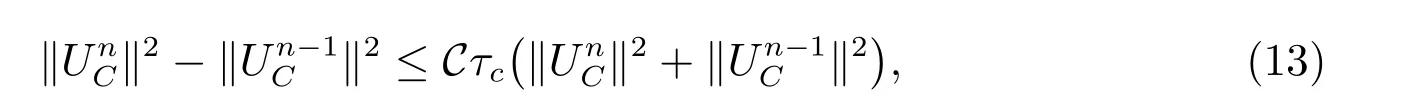
不等式兩邊從1加到n，得

再根據離散的Gronwall不等式，(8)式得證.

第二步，TT-M系統(7)式的等價形式為

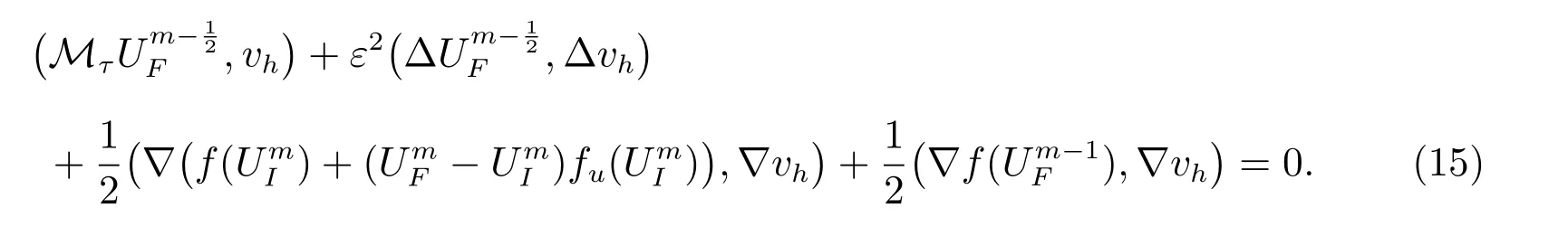
在(15)式中，令

類似于(8)式，有

為了估計‖UkI‖2，使用下面的拉格朗日插值公式

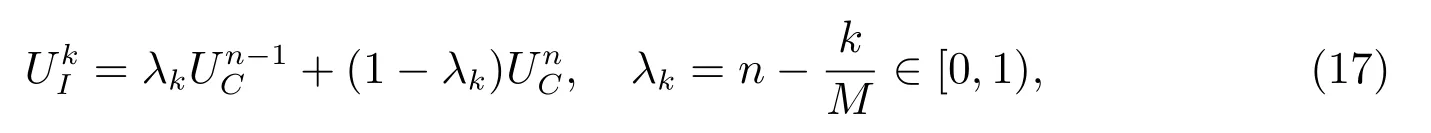
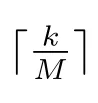
結合(16)式和(18)式，并根據離散的Gronwall不等式，(9)式得證.

5 誤差估計

為了對我們的數值格式進行誤差估計，引進下面的定義和引理.定義B(u,v)=ε2(Δu,Δv).

引理3[15]實數r滿足2≤r≤3，存在常數C與h無關，對任意函數

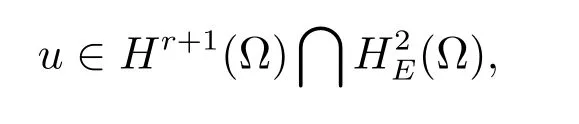
有

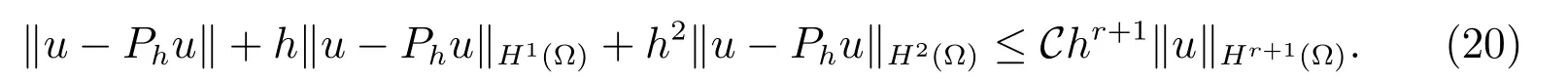
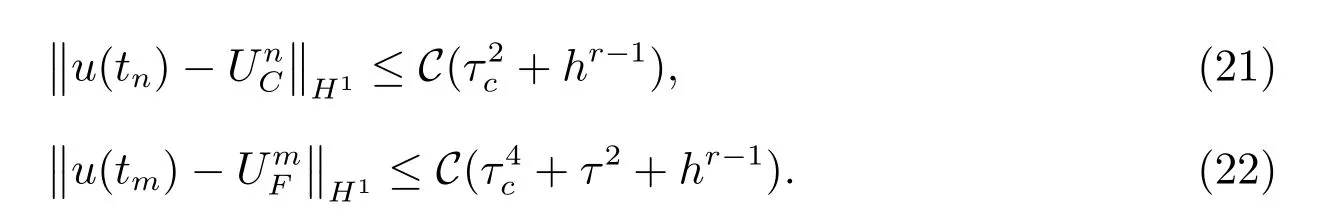
證明 首先，將初始問題(1)式等價于ut+Δ(ε2Δu?f(u))=0.其弱形式為

其中

下面分兩步證明：第一步，令

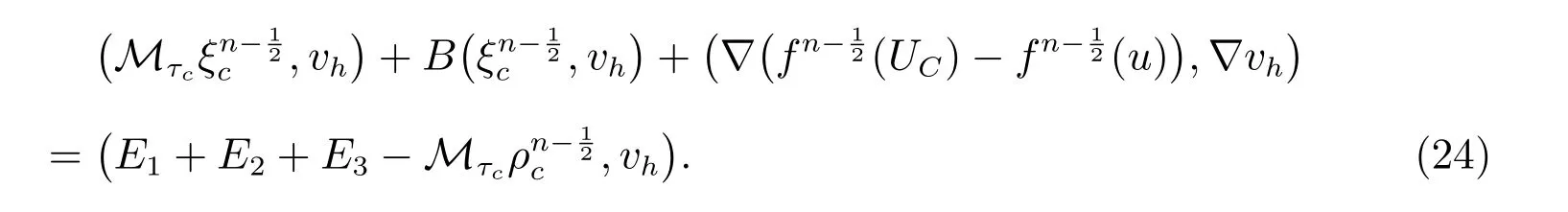
(25)式兩端從1加到n，可得

然后，根據離散的Gronwall不等式，可推得

最后，根據正交投影算子Ph的性質以及半范|u|H1和范數‖u‖H1的等價性質，(21)式得證.

第二步，首先估計時間細網格上的誤差‖u(tm)?UmI‖H1，由(17)式可得

其中?m∈(tn?1,tn)，結合(28)式和(21)式，由三角不等式得

將(23)式中n和τc替換為m和τ，再用(15)式減去所得結果得：對任意的vh∈Vh，有

其中

然后，使用泰勒展開式估計上式右端第一項，可得

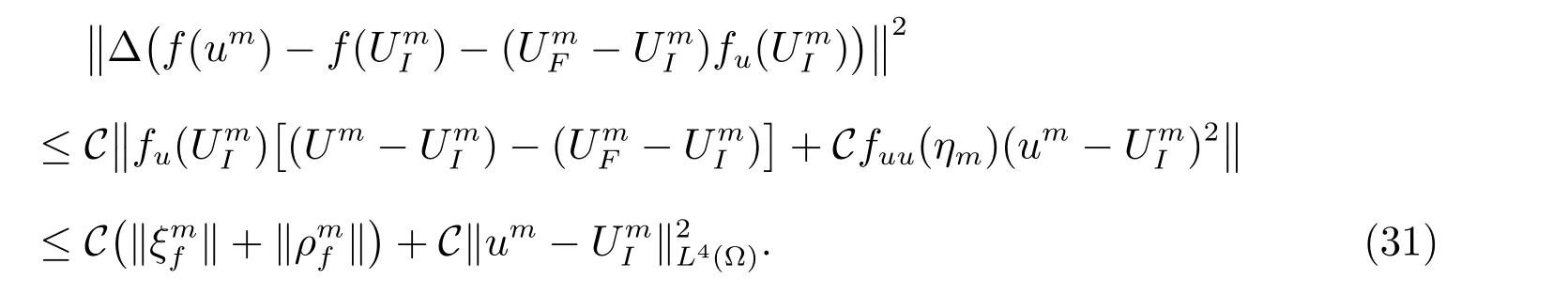
結合(30)和(31)，類似于(21)式，可推得

最后，根據正交投影算子的性質，半范|u|H1和范數‖u‖H1的等價性質，(22)式得證.

6 數值分析

在數值實驗部分，采用數值例子驗證理論分析的正確性和有效性.選擇初始條件和精確解分別為

u0=cos(πx)cos(πy)e,u(x,y,t)=cos(πx)cos(πy)ecos(t),

計算區域為[0,2π]×[0,2π].

6.1 空間與時間收斂階

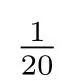
表1 TT-M FE方法的空間收斂階τc=10τ=

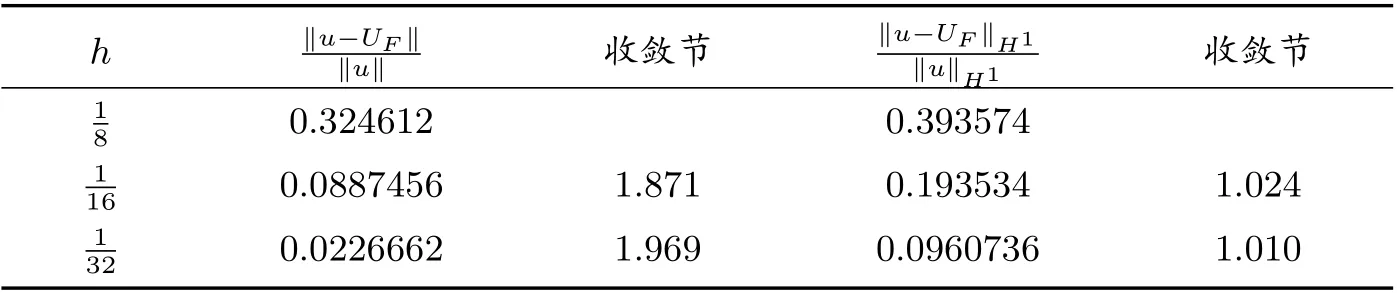
表1 TT-M FE方法的空間收斂階τc=10τ=

h ‖u?UF‖‖u‖ 收斂節 ‖u?UF‖H 1‖u‖H 1 收斂節1 8 0.324612 0.393574 1 16 0.0887456 1.871 0.193534 1.024 1 32 0.0226662 1.969 0.0960736 1.010

表2中，給出了當ε=1,M=2,h=τ2時的L2相對誤差和H1相對誤差.由表2可知，關于時間的H1相對誤差是二階收斂的，同理論分析部分一致.

表2 TT-M FE方法的時間收斂階h=τ2

6.2 TT-M FE方法和Galerkin FE方法的CPU耗時比較

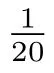
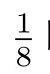
表3 TT-M FE方法和Galerkin有限元方法的CPU耗時

6.3 TT-M FE方法數值解UF和精確解u的比較

圖1精確解u

圖2 TT-M FE解UF

6.4參數M對CPU和誤差的影響

圖3中，當M從2增大到20時，TT-M FE方法的CPU耗時逐漸減小，趨于平穩.這表明用TT-M FE方法求解Cahn-Hilliard方程時，可以選擇較大參數M以提高數值求解的速度.

圖3 M對計算時間的影響

圖4中，隨著參數M的增大，TT-M FE方法的L2相對誤差在很小的范圍內波動，這表明參數M對數值計算的精度有較小的影響.

圖4 M對誤差的影響

7 結論

本文對Cahn-hilliard方程的時間雙層網格有限元方法進行了研究.從理論上證明了該方法的穩定性和誤差估計.最后通過數值例子驗證該方法的有效性和可行性.