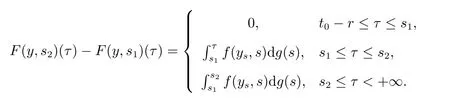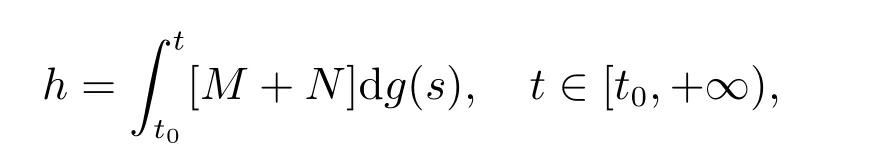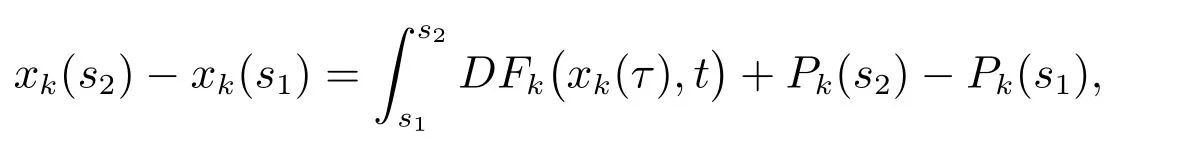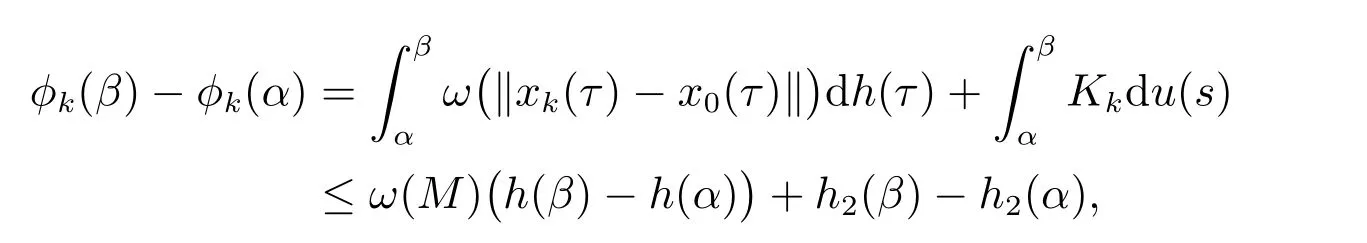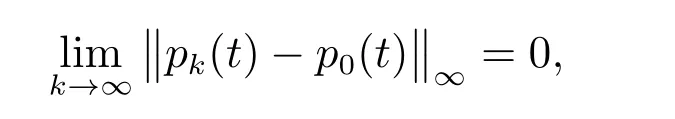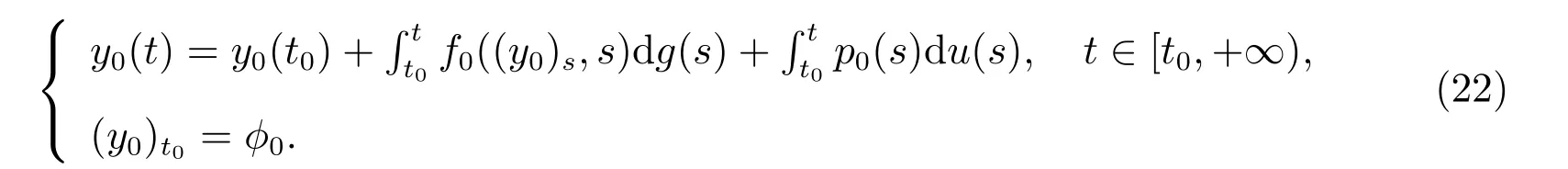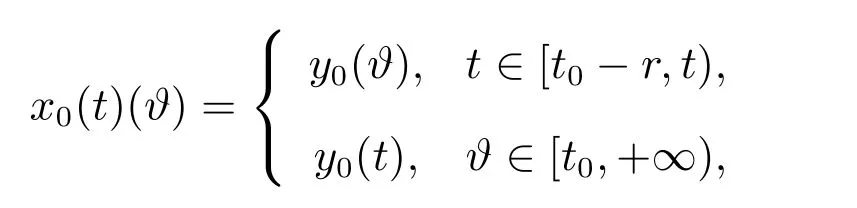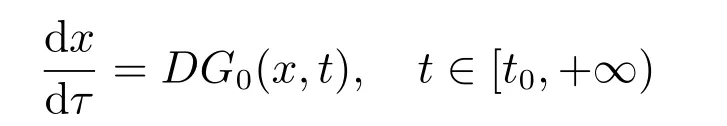滯后型測度泛函微分方程解對參數的連續依賴性

李寶麟, 楊萬秀

(西北師范大學數學與統計學院，蘭州 7 30070)

1 引言

當常微分方程˙x=f(x,t)所描述的系統受到擾動時，對受到擾動的系統導出的常微分方程的形式為

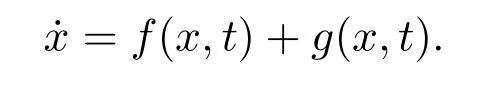
如果擾動項是連續可積的，那么擾動后的系統仍為常微分方程系統，它的解為連續的，若擾動項為脈沖型的，則擾動后的系統的狀態就不隨時間連續變化，而是呈現一種瞬時性態，對這種數學模型的研究導出另一種方程即測度微分方程，其一般形式為

在文獻[1]中，Kurzweil在1957年首次提出了廣義常微分方程理論.Schwabik在文獻[2]中研究了廣義常微分方程解對參數的連續依賴性，并在一定條件下建立了測度微分方程與廣義常微分方程的等價關系.在文獻[3]中介紹了Banach空間中廣義線性微分方程解對參數的連續依賴性.文獻[4,5]建立了在一定條件下測度泛函微分方程與廣義常微分方程的等價關系，并對解的存在唯一性及解關于初值條件的可微性，以及時間尺度上的泛函動力方程的周期平均化做了系統研究.文獻[6]證明了在抽象的Banach空間中廣義常微分方程解的存在性和唯一性，并證明了廣義常微分方程的解關于初值和參數的連續依賴性.

考慮滯后型測度泛函微分方程

和它所描述的系統受到擾動后的滯后型測度泛函微分方程

其中方程(2)等價于積分方程

方程(3)等價于積分方程

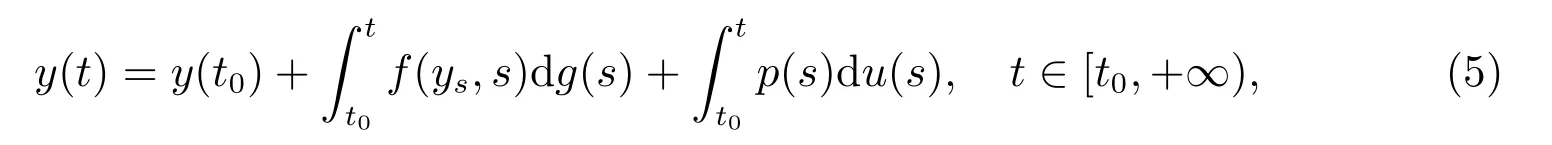
且方程(4)和方程(5)右端的積分是關于不減函數g,u:[t0,+∞)→R的Kurzweil-Stieltjes積分.

文獻[7]建立了在一定條件下滯后型測度泛函微分方程與廣義常微分方程的等價關系，研究了滯后型測度泛函微分方程的積分穩定性，其中Dy,Dg,Du分別是y,g,u的分布導數，函數f:T×[t0,+∞)→Rn,g,u:[t0,+∞)→R,y:[t0?r,+∞)→Rn,yt(θ)=y(t+θ),θ∈[?r,0],r>0,p:[t0,+∞)→Rn，且T={yt:y∈O,t∈[t0,+∞)}?G([?r,0],Rn),O?G([t0?r,+∞),Rn)是開集，G([t0?r,+∞),Rn)表示[t0?r,+∞)到Rn的所有有界正則函數全體，其中的范數為

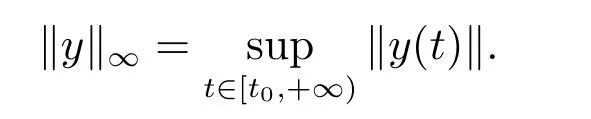
而且f與p滿足如下條件：

(H2): 對任意的y∈O,s1,s2∈[t0,+∞)，存在一個常數M>0，使得

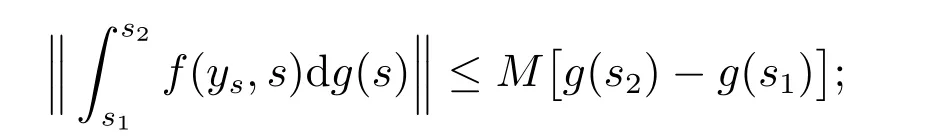
(H3): 對任意的y,z∈O,s1,s2∈[t0,+∞)，存在一個常數N>0，使得

(H5): 對任意的t∈[t0,+∞),s1,s2∈[t0,+∞)，存在一個常數K>0，使得

本文研究方程(2)和(3)在滿足(H1)–(H5)的條件下解對參數的連續依賴性.

本文主要包括三部分：第2部分重點介紹文中所要用到的基本概念及已有結果；第3部分給出滯后型測度泛函微分方程(2)和(3)解對參數的連續依賴性定理.

2 預備知識

定義2[2]函數U:[a,b]×[a,b]→Rn在區間[a,b]上是Henstock-Kurzweil可積的，如果存在I∈Rn，使得對任意的ε>0，存在正值函數δ(t):[a,b]→(0,+∞)，使得對[a,b]的任何δ-精細分劃D=(τj,[αi?1,αi]),j=1,2,···,k，其中τj∈[αi?1,αi]?[τj?δ(τj),τj+δ(τj)]，有

特別地，當f:[a,b]→Rn，且g:[a,b]→R,U(τ,t)=f(τ)g(t)時，

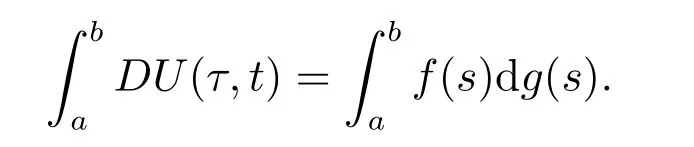
設F:Ω→Rn,Ω=O×[t0,+∞).

定義3[2]設函數F:Ω→Rn，如果x:[α,β]→Rn是廣義常微分方程

在區間[α,β]?[t0,+∞)上的解，是指對所有的t∈[α,β],(x(t),t)∈Ω，任意的s1,s2∈[α,β]，有

定義4[1]設函數h:[t0,+∞)是不減左連續的，ω:[0,+∞)→[0,+∞)是連續單調遞增函數且ω(0)=0，函數F:Ω→Rn，屬于函數族F(Ω,h,ω)是指F滿足以下條件，對任意的(x,s1),(x,s2)∈Ω，有

對任意的(x,s1),(x,s2),(y,s1),(y,s2)∈Ω，有

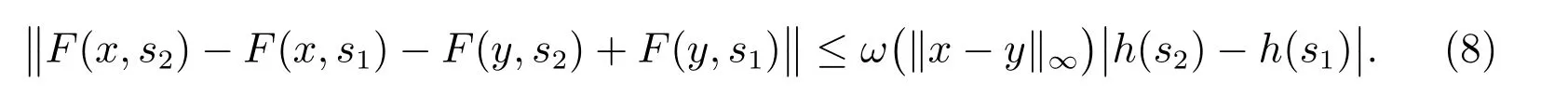
引理1[7]以下條件是等價的：

1)A是集合且A?G([α,β],Rn)是相對緊集；

2) 對每個x∈A,t1,t2∈[α,β]，集合{x(α);x∈A}是有界的且存在連續增函數ω:[0,∞)→[0,∞),ω(0)=0，及不減函數h:[α,β]→R，使得

引理2[6]設X是一個Banach空間，O?X是開集，G=O×[a,b]，h是不減的左連續函數，ω連續增加函數，函數列Fk:O×[a,b]→X，對每個k∈N0,(x,t)∈G,Fk∈F(G,h,ω)，有

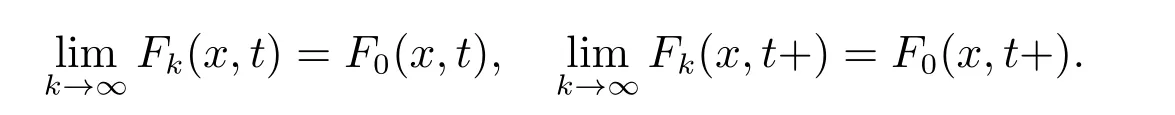
若存在一個序列函數xk:[t0,+∞)→O,k∈N0，使

且對每個t∈[t0,+∞)，有limk→∞xk(t)=x0(t)，則有

注1[7]若O是G([t0,+∞))的子集，稱O具有延拓性質，是指對于每個y∈O,ˉt∈[t0,+∞)，都有ˉy∈O，其中函數ˉy定義如下

引理3[7]設f:T×[t0,+∞)→Rn滿足(H1)–(H3).函數g:[t0,+∞)→R為不減的函數，對于y∈O,t∈[t0,+∞)，定義如下函數

則F∈F(Ω,h)，其中F:Ω→G([t0?r,+∞),Rn).

引理4[7]設O?G([t0?r,+∞),Rn)是開集，且t∈[t0,+∞)時具有延拓性質，T={yt:y∈O,t∈[t0,+∞)},φ∈T,g:[t0,+∞)→R是不減函數，f:T×[t0,+∞)→Rn滿足(H1)–(H3)，F:O×[t0,+∞)→G([t0?r,+∞),Rn)由公式(9)給定.

(i) 假設對于任意的y∈O,t∈[t0,+∞)，如果y:[t0?r,+∞)→O是滯后型測度泛函微分方程

的解.

對任意的t∈[t0?r,+∞)，有

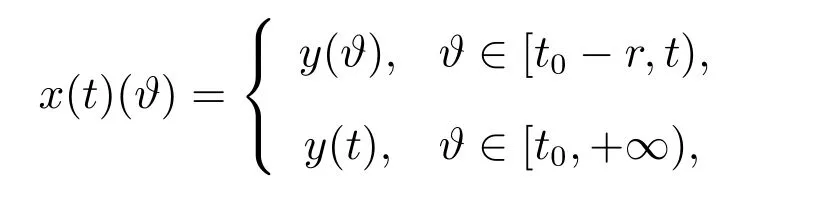
的解，其中F由(9)式給定.

(ii) 相反地，F由(9)式給定，如果x:[t0,+∞)→O是廣義常微分方程

的解，且滿足初值條件

則函數y:[t0?r,+∞)→O是滯后型測度泛函微分方程

在初值條件

的解.

引理5[7]設f:T×[t0,+∞)→Rn滿足(H1)–(H3)，且p:[t0,+∞)→Rn滿足(H4),(H5)，函數g,u:[t0,+∞)→R為不減的，對于y∈O,t∈[t0,+∞)，定義如下函數

則有

且G∈F(Ω,h)，其中G:Ω→G([t0?r,+∞),Rn).

引理6[7]設O?G([t0?r,+∞),Rn)是開集，且t∈[t0,+∞)時具有延拓性質，T={yt:y∈O,t∈[t0,+∞)},φ∈T,g,u:[t0,+∞)→R是不減函數，f:T×[t0,+∞)→Rn滿足(H1)–(H3)，且p:[t0,+∞)→Rn滿足(H4),(H5)，G:O×[t0,+∞)→G([t0?r,+∞),Rn)由(13)給定.

(i) 假設對于任意的y∈O,t∈[t0,+∞)，如果y:[t0?r,+∞)→O是滯后型測度泛函微分方程

的解.

對任意的t∈[t0?r,+∞)，有

下的解，其中G由(13)式給定.

(ii) 相反地，G由(13)式給定，如果x:[t0,+∞)→O是廣義常微分方程

的解，且滿足初值條件

則函數y:[t0?r,+∞)→O是滯后型測度泛函微分方程

在初值條件

的解.

3 主要結果

本節，將討論滯后型測度泛函微分方程(2)與受到擾動后的滯后型測度泛函微分方程(3)解對參數的連續依賴性.

定理1 設I?G([t0?r,+∞),Rn)是閉子集，O?I是開集，函數列Fk:O×[t0,∞)→Rn，對每一個k∈N0,(x,t)∈O×[t0,∞),Fk∈F(O×[t0,∞),h,ω)，有

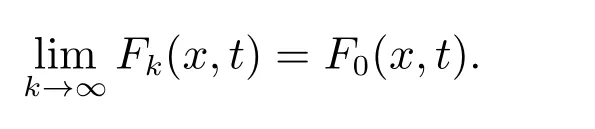
若存在一個序列函數xk:[t0,+∞)→O,k∈N0,t∈[t0,+∞)，使

且對每個t∈[t0,+∞)，有limk→∞xk(t)=x0(t)，則有

證明 由定義3知，對s1,s2∈[t0,+∞),k∈N0，有

由引理2知

則Fk∈F(O×[t0,∞),h,ω)，故對k∈N0[α,β]?[s1,s2]，有

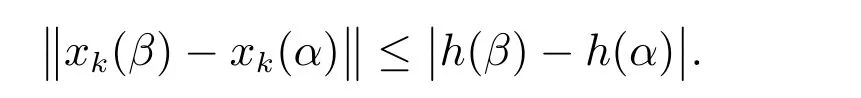
從而，當k→∞時，有

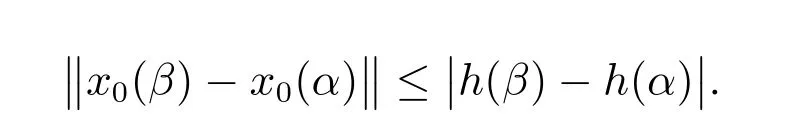
因h是正則的，故x0是正則的，即x0是有界變差的.又

存在，則

因為

從而，上式第二個積分當k→∞時一致收斂于0.又

因為，對k∈N0,s1,s2∈[t0,+∞)，有

其中

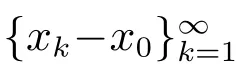
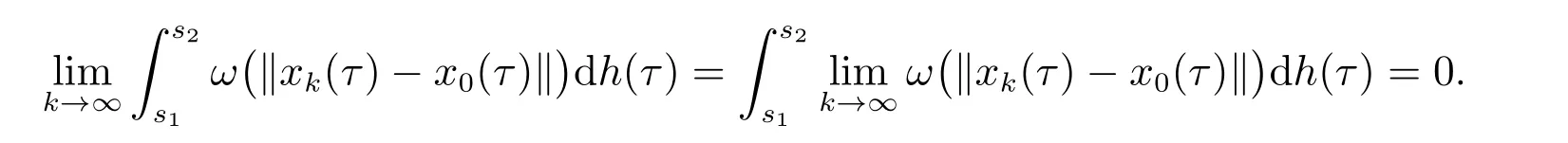
令

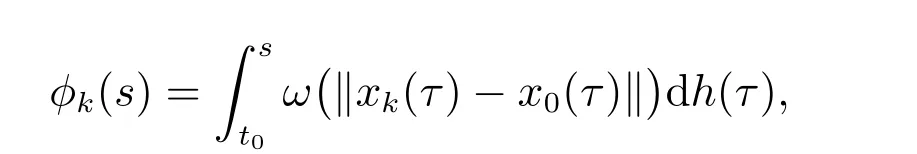
定理2 設I?G([t0?r,+∞),Rn)是閉子集，O?I是開集且具有延拓性質，T={yt:y∈O,t∈[t0,+∞)},g:[t0,+∞)→R是不減函數，ω:[0,+∞)→[0,+∞)是連續增加函數f:T×[t0,+∞)→Rn滿足(H1)–(H3)，F:O×[t0,+∞)→G([t0?r,+∞),Rn)由(9)給定，則F∈F(O×[t0,+∞),h,ω)，其中h是不減的左連續函數，且

函數列fk:T×[t0,+∞)→Rn,k∈N0滿足以下條件：

2) 對任意的y∈O,s1,s2∈[t0,+∞)，存在一個常數M>0，使得

3) 對任意的y,z∈O,s1,s2∈[t0,+∞)，存在一個常數N>0，且存在一個連續增加函數ω:[0,+∞)→[0,+∞),ω(0)=0，使得

4) 對任意的y∈O,t∈[t0,+∞)，有

5) 對每個k∈N0,x∈O,t∈[t0,+∞)，函數Fk:O×[t0,+∞)→G([t0?r,+∞),Rn)，如下給定

考慮到函數列φk∈T,k∈N0，使得在區間[?r,0]上有

若存在一個k∈N0，函數列yk是Fk的解如下形式

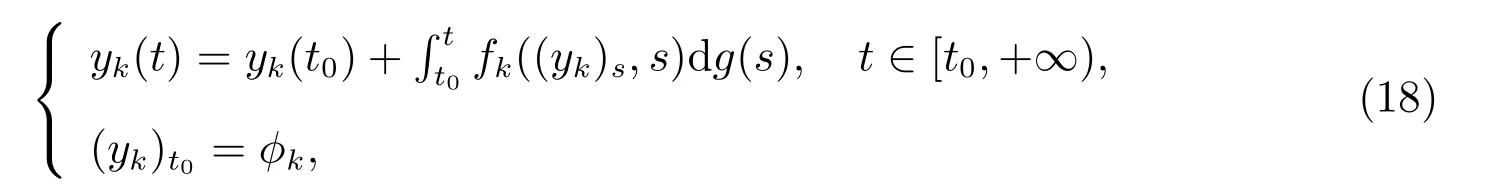
則存在一個函數y0∈O，使得在[t0,+∞)上有limk→∞‖yk?y0‖=0，則y0是F0的解如下形式

證明 由條件(H1)可知，定義的F積分存在，對任意的y∈O,t0≤s1

因此，對任意的y∈O,t0≤s1

由定義4及(H3)條件，如果y,z∈O,t0≤s1

由定理1知對每個x∈O,t∈[t0,+∞)，有limk→∞Fk(x,t)=F0(x,t)，通過奧斯古德定理[6]，對每個x∈O,t∈[t0,+∞)，有limk→∞Fk(x,t+)=F0(x,t+)，而且因為I是閉子集即有F0(x,t)∈I.由前面證明可知，對每個k∈N0,Fk∈F(O×[t0,+∞),h,ω)，其中h是不減的左連續函數，且對

又因為limk→∞Fk(x,t)=F0(x,t)，則有F0∈F(O×[t0,+∞),h,ω)，對k∈N0,t∈[t0,+∞)，令

由xk的定義，對于t∈[t0,+∞)，有limk→∞xk(t)=x0(t)，根據定理1，x0是

的解，故而確保y0滿足

因此，我們通過運用廣義常微分方程與滯后型測度泛函微分方程的等價關系，得到了方程(2)的解對參數的連續依賴性定理.

定理3 設I?G([t0?r,+∞),Rn)是閉子集，O?I是開集，函數列Gk:O×[t0,∞)→Rn，對每一個k∈N0,(x,t)∈O×[t0,∞),Gk∈F(O×[t0,∞),h,ω)，有limk→∞Gk(x,t)=G0(x,t).若存在一個序列函數xk:[t0,+∞)→O,k∈N0,t∈[t0,+∞)，使

且對每個t∈[t0,+∞)，有limk→∞xk(t)=x0(t)，則有

證明 由文獻[7]知對s1,s2∈[t0,+∞),k∈N0，有

顯然由定理1知

則Fk∈F(O×[t0,∞),h,ω)，故對k∈N0,[α,β]?[s1,s2]，有

從而，當k→∞時，有

因h,h2正則的，故x0正則的，即x0是有界變差的.又

存在，則

因為

從而上式第二個積分當k→∞時，一致收斂于0.又

因為對k∈N0,s1,s2∈[t0,+∞)，有

其中

且

由于h2是不減函數，則h2是有界變差的，故是正則的，則對k∈N0,t∈[t0,+∞),Pk∈G([t0?r,+∞),Rn)，有limk→∞‖Pk(t)?P0(t)‖∞=0，因此，對s∈[t0,+∞),k∈N，令

定理4 設I?G([t0?r,+∞),Rn)是閉子集，O?I是開集，g,u:[t0,+∞)→R是不減函數，T={yt:y∈O,t∈[t0,+∞)},f:T×[t0,+∞)→Rn滿足(H1)–(H3)，P:[t0,+∞)→Rn滿足(H4)和(H5)，G:O×[t0,+∞)→G([t0?r,+∞),Rn)由(13)給定，則有G∈F(O×[t0,+∞),h,ω)，其中h=h1+h2是不減的左連續函數，且

證明 由條件(H1)可知，定義的F積分存在，對任意的y∈O,t0≤s1

由條件(H4)可知，定義的P積分存在，故對任意的y∈O,t0≤s1

因此，由定理2知對任意y∈O，且t0≤s1

且有

同理，由定理2知，如果y,z∈O,t0≤s1

故對任意的y∈O，且t0≤s1

由定義4及(H3)條件知，如果y,z∈O,t0≤s1

定理5 設I?G([t0?r,+∞),Rn)是閉子集，O?I是開集且具有延拓性質，T={yt:y∈O,t∈[t0,+∞)},g,u:[t0,+∞)→R是不減的函數，函數列fk:T×[t0,+∞)→Rn,pk:[t0,+∞)→Rn,k∈N0滿足以下條件：

2) 對任意的y,z∈O,s1,s2∈[t0,+∞)，存在一個常數N>0且存在一個連續增加函數ω:[0,+∞)→[0,+∞),ω(0)=0，使得

3) 對任意的y∈O,t∈[t0,+∞)，有

5) 對每個k∈N0,s1,s2∈[t0,+∞)，存在一個常數K>0，使得

6) 對任意的y∈O,t∈[t0,+∞)，有

7) 對每個k∈N0,x∈O,t∈[t0,+∞)，函數Gk:O×[t0,+∞)→G([t0?r,+∞),Rn)，如下給定

函數Pk∈G([t0?r,+∞),Rn),k∈N0如下給定

則有

考慮到k∈N0,t∈[t0,+∞),Pk∈G([t0?r,+∞),Rn)，有

且存在函數列φk∈T,k∈N0，使得在區間[?r,0]上有limk→∞‖φk?φ0‖∞=0.

若存在一個k∈N0，函數列yk是Gk的解如下形式

則存在一個函數y0∈O，使得在[t0,+∞)上有limk→∞‖yk?y0‖=0，則y0是G0的解如下形式

證明 由定理1可知，對每個x∈O,t∈[t0,+∞)，有limk→∞Fk(x,t)=F0(x,t)，且F0∈F(O×[t0,+∞),h,ω)，又有k∈N0,t∈[t0,+∞),Pk∈G([t0?r,+∞),Rn)，則有

從而P0∈G([t0?r,+∞),Rn)，故對每個x∈O,t∈[t0,+∞)，有limk→∞Gk(x,t)=G0(x,t)，根據奧斯古德定理對每個x∈O,t∈[t0,+∞)，有limk→∞Gk(x,t+)=G0(x,t+)，而且因為I是閉子集即有G0(x,t)∈I.由定理3和定理4知，對每個k∈N0,Gk∈F(O×[t0,+∞),h,ω)，其中h=h1+h2是不減的左連續函數，且

由limk→∞Gk(x,t)=G0(x,t)，則有G0∈F(O×[t0,+∞),h,ω)，對k∈N0,t∈[t0,+∞)，令

由xk的定義，對于t∈[t0,+∞)有limk→∞xk(t)=x0(t)，根據定理3和定理4，對任意的t∈[t0,+∞)，有

是廣義常微分方程

的解，故而確保y0滿足