非校正相位延遲參數在復雜鐵路場景下GPS 精密單點定位應用研究

宋益橋，林春峰，趙兵，郭剛，郜珂

(中鐵二院工程集團有限責任公司，成都 610031)

0 引 言

與其他交通運輸工具相比，高速鐵路在運輸貨物、載客能力和運載可靠性方面都可更好地滿足城市間的運輸需求[1].中國鐵路總公司近年發表的《中長期路網規劃》中指出，截止到2020 年鐵路總里程將達到150 000 km，重點加快西部鐵路建設，進而實現構建“八縱八橫”的全國高速鐵路主通道[2-3].與此同時，對高速鐵路修建與維護各階段也提出了更高的要求.隨著全球衛星導航系統(GNSS)的發展，其載波相位差分技術(RTK)和網絡RTK 已在鐵路建設中得到了較好地應用，在很大程度上替代了鐵路場景下的傳統精密測量，如武瑞宏等[4]基于網絡RTK技術構建了鐵路BDS/GNSS 高精度位置服務平臺，對鐵路工程GNSS 基準站網的建設具有重要意義；張云龍[5]設計了嚴寒地區鐵路運行期路基北斗衛星導航系統(BDS)遠程變形監測系統，實現了外符合精度可達mm 級的變形監測目標.但RTK 技術的顯著缺點是需要建立密集或者近距離的基準站進行輔助，不利于大范圍的山區、森林以及復雜艱險地區作業[6-8].而近十幾年發展起來的精密單點定位(PPP)因其無需架設基站，可靈活高效地實現全球任意范圍內高精度位置信息的獲取，被認為是繼RTK 和網絡RTK 后的全新精密定位模式，并且在增強PPP 條件下可進一步提升定位精度和縮短卡爾曼濾波收斂時間[9-10].當前利用該項技術對鐵路場景下基準站的應用和研究還相對較少，特別是在復雜的觀測環境.

因此，本文首先基于空間衛星跟蹤數、衛星位置精度因子(PDOP)和定位殘差三個方面對鐵路場景下觀測數據質量的可靠性進行評估；然后基于高精度的衛星載波相位信號觀測值，利用相位偏差參數重點對鐵路場景下GPS 的PPP 應用進行相關研究.

1 PPP 定位原理

當衛星端發射的信號穿過大氣層到達用戶端時，將依次受到電離層延遲、對流層折射和多路徑效應等影響，在綜合顧及到各頻率上各種類型偏差的影響下，PPP 原始觀測值方程[11]可表述如下：

在實際數據處理過程中，無電離層組合可消除電離層延遲一階項的影響，剩余延遲可被忽略，常用于PPP 組合觀測方程的建立.假設衛星和接收機端天線相位中心偏差(PCO)和天線相位中心變化(PCV)、衛星端相位纏繞、相對論效應以及地球自轉偏差已被精確改正[13].在引入精密星歷和鐘差后，如式(2)所示：

分析可知，該項參數吸收了衛星端和接收機端的偽距硬件延遲偏差和載波相位硬件延遲偏差，導致模糊度不再具有整數性質，在卡爾曼濾波或者最小二乘估計過程中，需要通過一定的時間才能獲得高精度的浮點解.

其中，式(2)～(4)中的各項參數可具體表示為

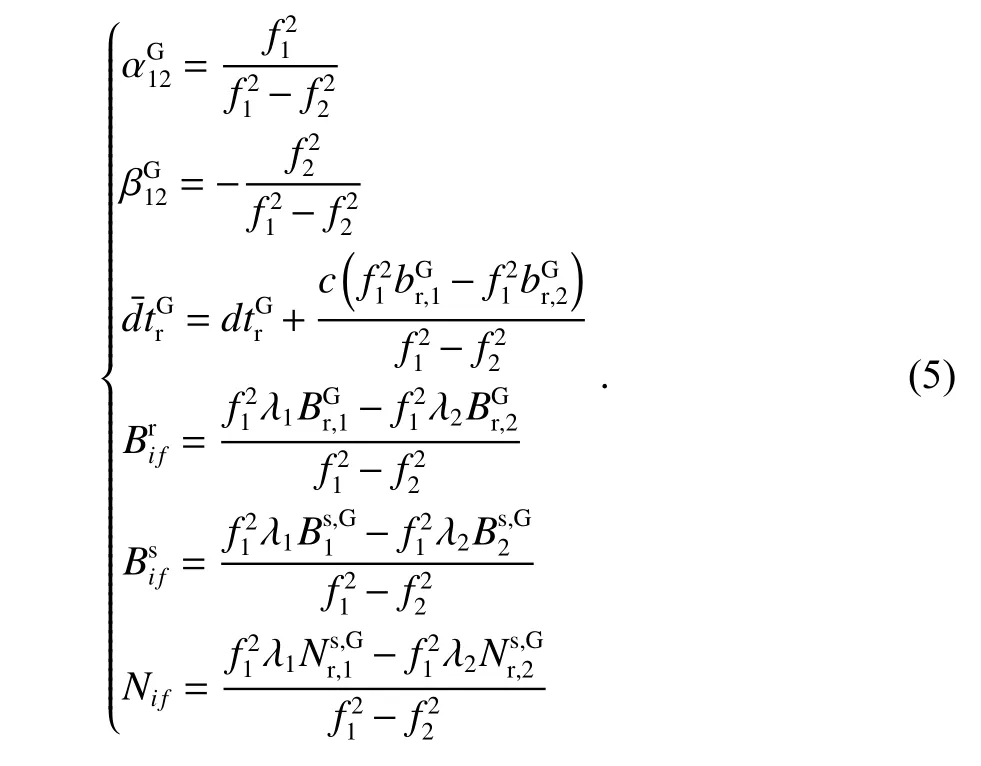
因為卡爾曼濾波后的浮點模糊度不具有整周特性，需要將其寫成具有整周特性的寬巷和窄巷的組合形式，如式(6)所示：

固定解PPP 技術的核心在于對式(7)中的updr,WL、進行消除和改正，得到浮點模糊度的固定解，進而對位置解和其他參數進行約束更新.其中，對于接收機端相位硬件延遲，可通過星間單差或選擇固定基準的方法進行消除[14]，而對于衛星端相位硬件延遲，可通過國內外GNSS 科研機構發布相應的偏差產品進行改正，并基于LAMBDA 算法實現模糊度固定.詳細的增強PPP 技術可參考文獻[12].

對于雙頻無電離層組合，在模糊度固定時需要分解成寬巷模糊度和窄巷模糊度，如式(7)所示.式中的寬巷非校正相位延遲(UPD)由于波長較長，未模型化的誤差對其影響較小，因此表現出長期的穩定性，可進行每天估計一值.而對于窄巷UPD，其相應的波長僅有10.7 cm，受到未模型化的誤差影響較為嚴重，可進行每15 min 或者30 min 估計一值.無論是寬巷UPD 還是窄巷UPD，由于他們均是由時變穩定的偏差組成，當誤差改正模型和算法合適，兩種估計值均具有較高的精度和較穩定的時間序列.

2 鐵路場景下的定位結果分析

實驗中以GPS 衛星系統為例，選取中國區域某個在建鐵路中斷的7 個GNSS 靜態觀測站，每個測站分別觀測兩個時段，每個時段的觀測時間約90 min.在收集到的7 個觀測站中，包括5 個一級控制點和2 個二級控制點，且測站間最遠水平距離小于50 km.觀測時間為2019 年的第214 天，接收機類型為TRIMBLE NETR4，采樣率為15 s.本文研究中采用歐洲定軌中心(CODE)分析中心發布的精密軌道和鐘差產品和武漢大學發布的UPD 相位偏差產品[15]，且各衛星PCO/PCV改正值均采用國際GNSS 服務(IGS)發布的天線文件.其中各級控制點觀測環境如圖1所示.

圖1 各級控制點觀測環境

2.1 衛星定位可用性評估

衛星精密定位和導航的精度與測站所能觀測到的衛星顆數以及所跟蹤衛星的PDOP 值密切相關，即可視衛星顆數和PDOP 值可反映導航衛星系統的適用性和服務能力，其中可見衛星有助于提高定位精度的可靠性，而PDOP 值是衡量衛星導航系統定位精確程度的一個重要指標.因此，本文對所收集到的14 個觀測時段的PODP 值進行計算和對所跟蹤到的衛星數進行統計.限于篇幅，圖2 中只給出了一級控制點和二級控制點的衛星天空軌跡圖.

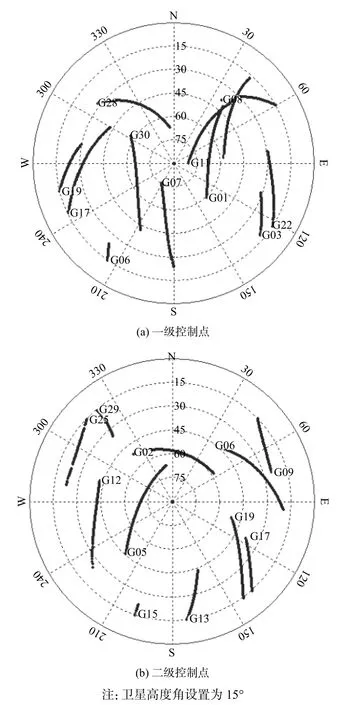
圖2 控制點處的天空軌跡圖

如圖2 所示，圖2(a)、(b)分別展示了兩個不同級別控制點在不同時間段內的衛星天空分布軌跡圖.分析可知，當衛星高度角設置為15°時，在觀測時間段內各測站可連續跟蹤到5 顆以上的衛星，能較好地滿足測量區域全天候、高精度的PPP，且各衛星高度角分布適中.為了詳細地分析各測站在整個觀測時間段內的衛星可用性，分別統計了所有歷元的衛星顆數和PDOP 值，并計算得到每個測站所在觀測時間段內的平均值，如表1 和表2 所示.

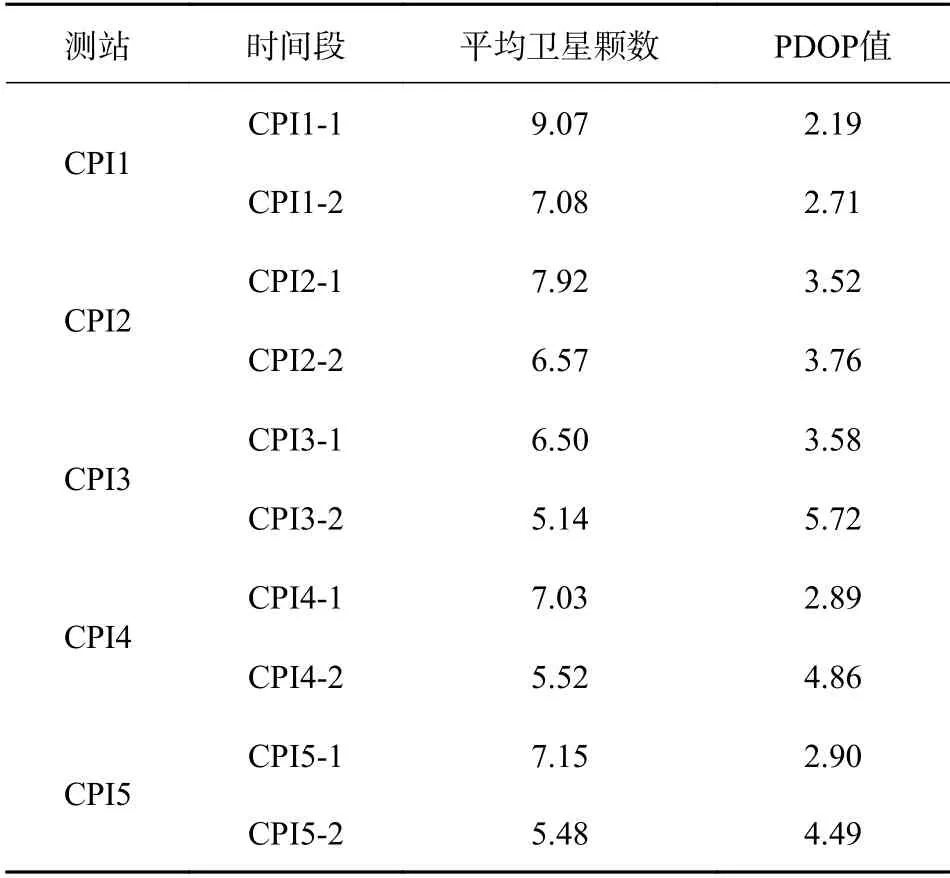
表1 一級控制站不同時段內可視衛星平均顆數和平均PDOP 值 cm

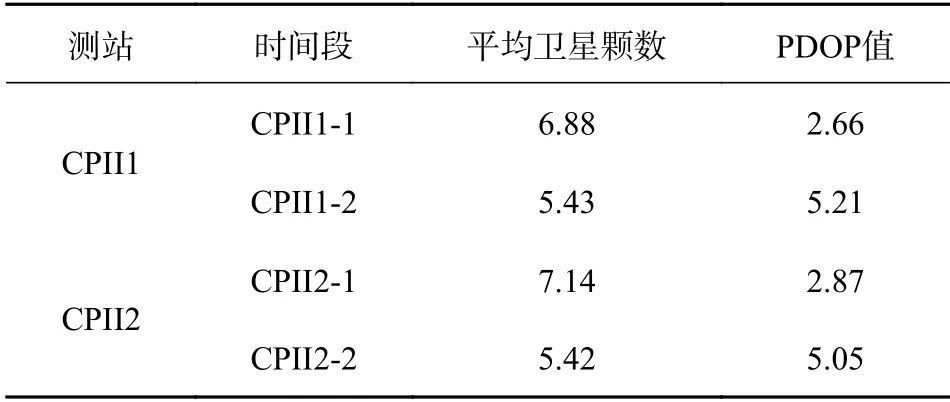
表2 二級控制站不同時段內可視衛星平均顆數和平均PDOP 值 cm

總體分析可知，各測站在所有時間段內可跟蹤到的衛星平均數分布在5.14～9.07 顆，在整個測區內可平均跟蹤到6.60 顆衛星，可較好地滿足地基增強PPP 定位的需求；對于衛星PDOP 值，其平均值約分布在2.19～5.72 顆，整個測區內的平均值約3.74 cm，說明具有良好的空間衛星定位環境，保證了可靠的定位基準.但對于同一測站在兩個時間段內所跟蹤衛星數和PDOP 值有所差異，且第二個觀測時間段內略差于第一個觀測時間段，原因可能是由于鐵路特殊的觀測環境，部分衛星在運動過程中受到了某些建筑物或者山體等的遮擋，特別是CPI3 測站更為顯著.因此在測站精密位置解算過程中，需要利用卡爾曼濾波或最小二乘進行靜態迭代計算.此外，分析可知，二級測站處的觀測環境差于一級處的測站，這是由于二級測站通常布設在周圍多山體和構筑物的地理位置，而更高級的控制點通常布設在通視環境相對較好的位置.綜上所述，在整個測區內任意位置可實現GPS 單系統的高精度定位，僅有少部分歷元受限于跟蹤衛星顆數和較差的PDOP 值.

為了進一驗證觀測數據的可靠性，本文分別對同一個測站兩個不同觀測時間段的數據進行雙差解算，采用的軟件為GAMIT/GLOBK 10.7.解算時的衛星高度角同樣設置為15°，潮汐改正模型為FES2004格網數據，對流層投影函數為VMF1 GMF，電離層延遲可通過無電離層延遲組合進行消除.平差過程中通過利用卡爾曼濾波進行逐歷元平滑解算，進而得到坐標解的高精度位置信息，最后將同一個測站不同觀測時間段的坐標值做差，進行坐標轉換得到不同觀測時段的互差值，如表3 所示.實際上對同一個測站，其在不同時段的定位坐標值應該相同，但由于未模型化的誤差導致坐標間存在一定差異.由表3 可知，三個方向的坐標差值均小于10 cm，特別是水平向，差值優于5 cm，說明在鐵路觀測環境下，當靜態觀測時間約為90 min 時，可較好地滿足定位精度的需求.

表3 測站不同觀測時間段測站差異 cm

2.2 顧及相位偏差的PPP 定位性能分析

無論是利用RTK 還是網絡RTK，或者是利用GAMIT/GLOBK 軟件解算測站點坐標，均需要額外的基準站提供差分數據或者是被用來進行雙差.當在鐵路環境等地形復雜的區域，往往在解算時需要付出較高的代價，甚至有時無法進行雙差解算，此時可利用固定的PPP 技術來有效地獲得待求測站精準位置信息.而對于固定PPP，其核心在于如何解算衛星端相位小數周偏差和浮點模糊度準確固定.本研究中采用武漢大學發布的相位小數周偏差產品，其寬巷UPD 每天估計一值，窄巷UPD 每15 min 估計一值[15].在模糊度固定時采用先全模糊度固定，當失敗時采取部分模糊度固定的策略.

圖3(a)～(b)中分別以一級控制點(CPI1)和二級控制點(CPII1-1)為例給出了浮點解和PPP 固定解在不同方向的殘差時間序列，其參考值選取為基于GAMIT/GLOBK 軟件的雙差解.分析可知，當模糊度固定后，其定位解明顯加快了精度的收斂，保持了定位解序列的穩定性，并且可進一步提高定位結果的可靠性.為了詳細地對比分析，表4 中給出了各測站在不同觀測時段內北(N)、東(E)和天(U)三個方向的浮點解和固定解坐標定位殘差，其計算方法為取最后60 個歷元的平均值.分析可知，模糊度固定后，其水平方向定位精度優于10 cm，高程方向優于15 cm，特別是在N 向，定位精度約優于5 cm，大幅度的提高了測站位置信息的可用性.經統計，相對于浮點PPP 解，固定的PPP 的定位精度在N、E、U 三個方向可分別提升約32.51%、42.78%、21.32%，定位精度有顯著改善.

圖3 固定解/浮點解不同方向的殘差時間序列

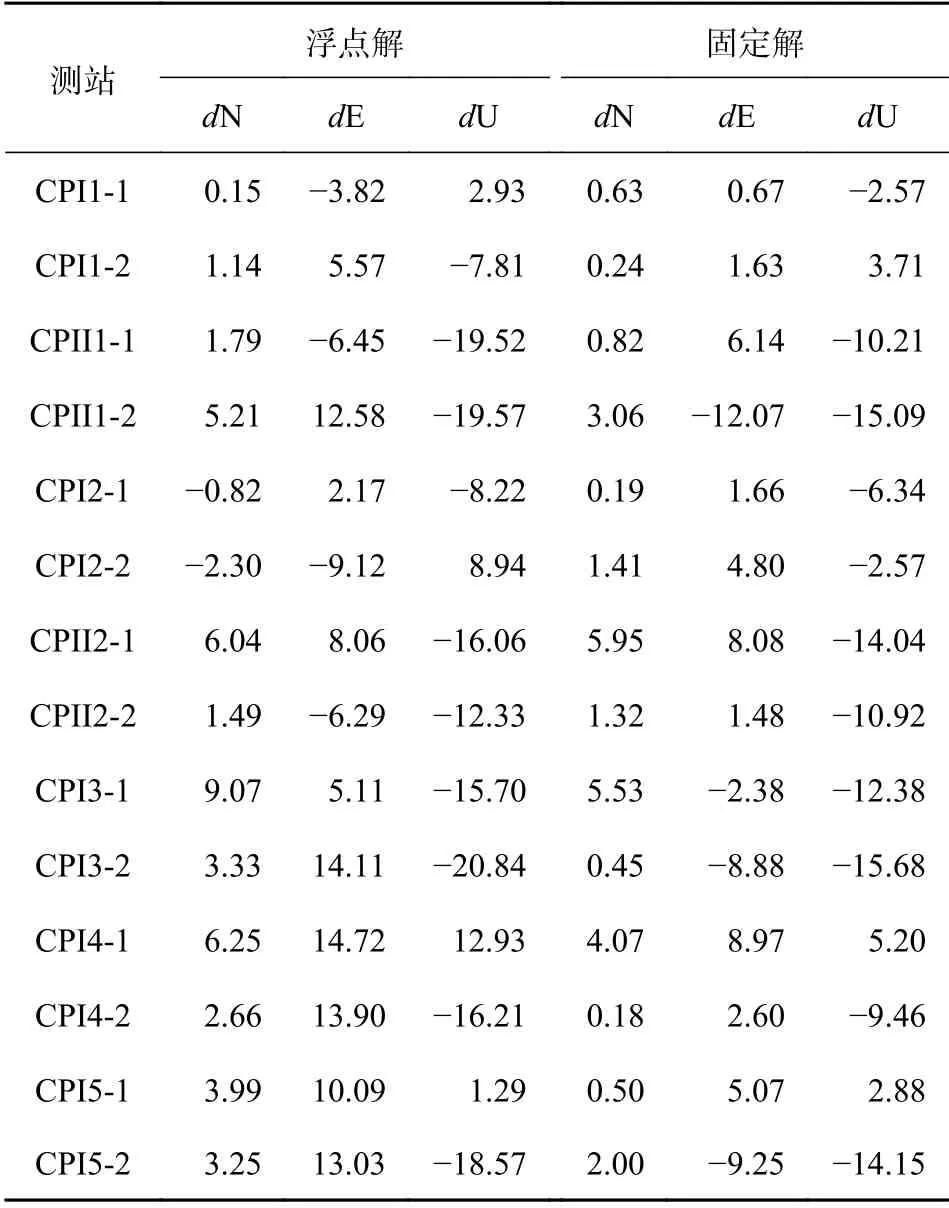
表4 各觀測時段浮點解和固定解三個方向坐標殘差 cm

同時，如圖4 所示，分別給出了各測站在不同時間段內浮點解和固定解的三維方向定位殘差，結果表明在鐵路環境下，固定的PPP 解可使得其三維方向上的定位精度提升約17.91%～57.98%，平均約為35.43%，實現了大部分測站優于10 cm 的靜態定位解.并且對水平方向上的提升效果更加明顯，如測站CPI4-2 和CPI1-2.說明固定的PPP 可明顯地改善鐵路復雜環境下靜態定位精度，進一步提升觀測數據的可靠性和高精度性.

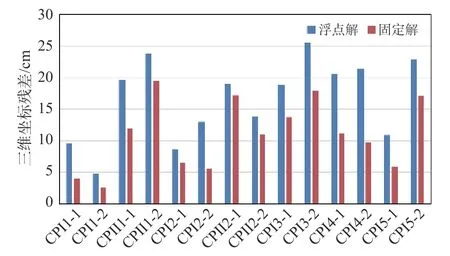
圖4 三維方向固定解和浮點解定位精度

3 結束語

鐵路是關系國計民生的重要戰略行業，而衛星導航定位系統是鐵路建設過程中不可或缺的重要技術.本文以單GPS 系統為例，分別從可視衛星顆數、PDOP 值以及固定解PPP 等方面研究了鐵路復雜觀測環境下的衛星可用性和PPP 定位性能.結果表明：1)測站在所有觀測時段的衛星數量和衛星定位幾何構型具有高可用性，其中在測區內跟蹤到的衛星平均顆數和平均PDOP 值分別約為6.60 cm 和3.74 cm，為實現PPP 固定解提供了較好的觀測環境；2)相對于浮點PPP，固定的PPP 解在定位收斂時間和位置殘差方面均得到顯著改善，其在水平方向和高程方向定位精度分別優于10 cm 和15 cm，特別是在N 方向，定義精度約優于5 cm，且三維方向上的定位精度可平均提升約35.43%.說明復雜的鐵路環境下，固定PPP 可進一步提升觀測數據的可靠性和位置信息的高精度性.

特別地，當前我國北斗三代衛星導航系統(BDS-3)已全面建成，其衛星數量和信號質量等方面有著明顯的提升.在復雜鐵路環境下，BDS/GNSS 組合定位必將提升空間可視衛星顆數和增強衛星觀測的幾何構型強度，以及提高PPP 的可用性.并且對于固定解的PPP，其在定位精度和收斂時間方面必將會進一步改善.