融入四元數變換的“計算方法”課程教學實踐

凌思濤 陳興同 王海軍 王瑞瑞 吳鋼

[摘 要] “計算方法”是高校理工科本科生的一門重要課程，它以介紹各類數值計算問題的算法基本原理和提供數值方法為主要內容，幫助學生提高解決實際問題的能力。詳細闡述在“計算方法”課程教學過程中，通過融入四元數的基本知識和變換技巧，形成延拓式的教學模式，結果表明，可以激發學生對本課程的學習興趣，從而提高他們的學習積極性，對拓展學生的知識視野、培養學生的創新思維和深入思考問題的能力有積極意義。

[關鍵詞] 計算方法;延拓式教學;四元數

[基金項目] 2019年度中國礦業大學教學研究項目一般項目“面向留學生的《計算方法B》英文課程教學研究與實踐”（2019YB32）

[作者簡介] 凌思濤（1980—），男，山東臨沂人，計算數學專業博士，中國礦業大學數學學院副教授，主要從事數值代數研究。

[中圖分類號] G642.4? ?[文獻標識碼] A? ? [文章編號] 1674-9324（2021）25-0076-04? ?[收稿日期] 2021-04-22

一、引言

“計算方法”是高校理工科本科生的一門重要課程，該課程又稱數值計算方法或數值分析，它以介紹各類數值計算問題的算法基本原理和提供數值方法為主要內容，向理工科學生傳授科學研究和工程技術中數值計算的基本知識，提高學生解決實際問題的能力。它更注重理論教學和實踐教學的有機融合，與計算機軟件相結合實施教學過程是本課程的一個特色。

隨著科學技術現代化進程的加速，科學計算在自然科學各領域中的地位變得非常重要，例如航空航天、大氣運動、橋梁鐵路工程、火車輪船制造、地質勘探、地震預報、風險投資等領域都需要用科學計算進行數據處理。除了理論研究和科學實驗以外，科學計算已經成為當前科學研究的三大方法之一[1] （P1-3）。“計算方法”是培養大學生將來能夠進行科學計算的入門級課程，隨著人們認知水平的提高和各領域學科的交叉互融，特別是大數據時代的到來，迫切需要人們提高科學計算的能力。然而，“計算方法”課程原有的教學內容已不能完全滿足學科發展的需要，傳統的教學模式和教學方法也不能充分調動學生的學習積極性。在切實掌握經典方法和理論的前提下，需要豐富“計算方法”的教學內容，改進教學方法，增加學生對“計算方法”課程的認同感，激發他們的學習興趣。

國家強調高校要注重培養具有創新意識、創新思維、創新能力和創新人格的創新型人才。自教育部頒布《面向21世紀教學內容和課程體系改革計劃》以來，教育工作者們從課堂教學和實驗教學等不同方面積極探索和實踐關于“計算方法”課程的教學研究與改革。近幾年，人們更加注重將“計算方法”的實踐教學與現實生活中遇到的實際問題進行結合，在教學過程中將最新的數學建模問題融入課堂教學[2]。在教學內容的改進方面，文獻[3]提出了將理論力學和材料力學中的實際問題作為引例融入“計算方法”的課堂教學，以提高學生分析問題和解決問題的能力。文獻[4]對整個課程進行統籌思考，提出了模塊化教學的理念。文獻[5]挖掘了PageRank算法的思想和“計算方法”課程中一些算法思想的共性，提出了將PageRank思想滲透到“計算方法”課程的課堂教學中和稀疏矩陣的實踐教學中，從而加深學生對冪法的理解和對稀疏矩陣稠密矩陣的認識。隨著網絡技術的發展，新的教學手段不斷涌現，基于網絡化教學的教學方法和教學手段的改革措施也應運而生[6]。還有很多其他改革舉措，這里不再逐一列舉。

本文主要從教學內容方面探討“計算方法”課程課堂教學的改革措施，結合作者多年來在四元數相關問題研究中的體會，倡導教學過程中要將教學工作和科學研究相結合，以科研促教學的理念。以經典Jacobi方法求解實對稱矩陣特征值的教學內容為例，介紹四元數變換在“計算方法”課程教學中的應用，總結形成了“計算方法”課程教學中延拓式教學模式的教學實踐。

二、四元數基本性質的引入

早在1843年，愛爾蘭數學家Hamilton為了描述多維空間中的物理現象而發明了四元數，它是最簡單的超復數。四元數是復數a+bi的推廣形式，一個四元數可以表示為q=q0+q1i+q2j+q3k，（1）

q0，q1，q2，q3∈R

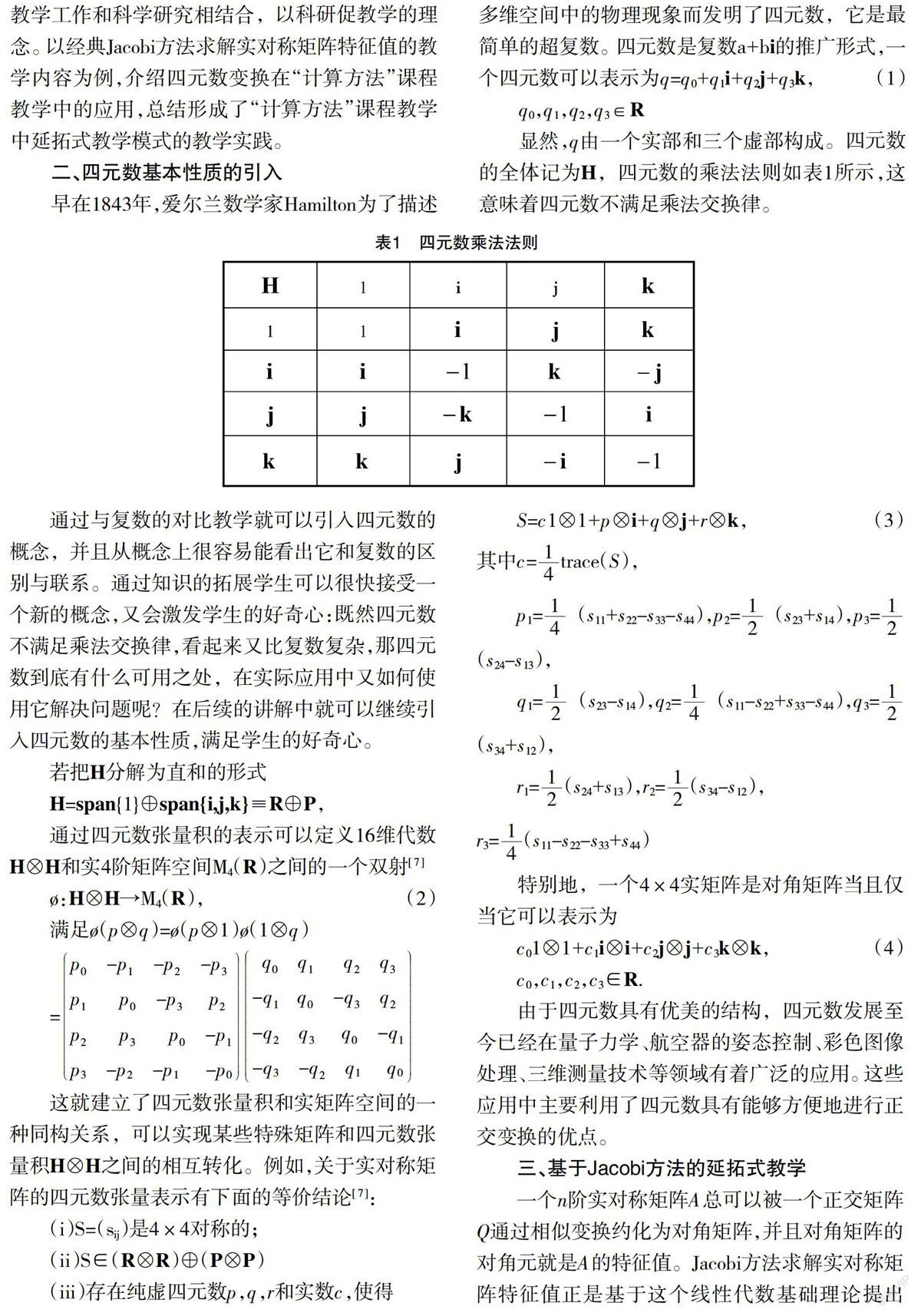
顯然，q由一個實部和三個虛部構成。四元數的全體記為H，四元數的乘法法則如表1所示，這意味著四元數不滿足乘法交換律。

通過與復數的對比教學就可以引入四元數的概念，并且從概念上很容易能看出它和復數的區別與聯系。通過知識的拓展學生可以很快接受一個新的概念，又會激發學生的好奇心：既然四元數不滿足乘法交換律，看起來又比復數復雜，那四元數到底有什么可用之處，在實際應用中又如何使用它解決問題呢？在后續的講解中就可以繼續引入四元數的基本性質，滿足學生的好奇心。

若把H分解為直和的形式

這就建立了四元數張量積和實矩陣空間的一種同構關系，可以實現某些特殊矩陣和四元數張量積H？塥H之間的相互轉化。例如，關于實對稱矩陣的四元數張量表示有下面的等價結論[7]：

特別地，一個4×4實矩陣是對角矩陣當且僅當它可以表示為

c0，c1，c2，c3∈R.

由于四元數具有優美的結構，四元數發展至今已經在量子力學、航空器的姿態控制、彩色圖像處理、三維測量技術等領域有著廣泛的應用。這些應用中主要利用了四元數具有能夠方便地進行正交變換的優點。

三、基于Jacobi方法的延拓式教學

一個n階實對稱矩陣A總可以被一個正交矩陣Q通過相似變換約化為對角矩陣，并且對角矩陣的對角元就是A的特征值。Jacobi方法求解實對稱矩陣特征值正是基于這個線性代數基礎理論提出的。正交矩陣Q的形成過程是通過一系列的正交旋轉變換使矩陣A的非對角元逐步收斂到零。這是從矩陣變換的角度來介紹Jacobi方法求解實對稱矩陣的特征值問題，以此問題為基礎，可以引導學生從四元數張量的角度實現算法，這是關于本部分知識的拓展環節，以期學生對Jacobi方法有更深入的理解。