懸浮彈多旋翼懸浮裝置翼間氣動干擾特性分析

張宏樂，錢建平，郭 淳，蘇文杰

(南京理工大學 機械工程學院， 南京 210014)

1 引言

懸浮彈是一種新型彈藥，被用于保護海上艦船目標和重要軍事工事而提出的一種新概念“被動式”低空防御武器。懸浮彈工作原理是由炮射母彈拋撒大量子彈，子彈依靠自身懸浮裝置實現短暫懸浮或減速下降，從而在指定空域構建懸浮彈幕群，實現對來襲目標的攔截與毀傷[1-2]。本文懸浮子彈升力由多旋翼懸浮裝置提供，因此懸浮子彈多旋翼間的氣動干擾特性研究對于提高子彈的懸浮能力具有重要意義。

對于旋翼氣動特性的研究，蘇京昭等人通過對不同結構參數的旋翼模型進行研究，得到單旋翼的結構參數對其氣動力的影響，為懸浮彈懸浮裝置旋翼結構參數的選擇提供了依據[1]。肖天航等人建立了低雷諾數非定常流場的數值方法，并將其應用于微型飛行器[3]。黃水林等人建立了對縱列式直升機雙旋翼氣動干擾特性分析的自由下洗流迭代方法，并對縱列式雙旋翼氣動干擾特性進行分析[4]。

懸浮彈采用多旋翼懸浮裝置提供彈體所需升力，因此必然存在旋翼間的氣動干擾，進而直接影響裝置懸浮能力。本文利用多重坐標系和動網格模型對GWS6030×2型單旋翼流場進行CFD仿真計算，并與理論值進行對比，證明該仿真模型在旋翼氣動力及流場計算的可靠性，并利用此CFD仿真方法研究旋翼間干擾對多旋翼氣動力特性的影響。分析旋翼結構參數對翼間氣動干擾的影響，從而為懸浮子彈的多旋翼懸浮裝置設計提供參考。

2 單旋翼流場與氣動特性CFD仿真

本文選取GWS6030×2型旋翼，通過建立多重參考坐標系(MRF)和動網格模型對旋翼旋轉過程中的氣動力特性進行仿真研究[5]。首先對旋翼進行幾何建模，利用多重坐標系構建其旋轉計算域和空氣計算域(即固定域)。通過ICEM對空氣計算域進行區塊劃分，對空氣計算域與旋轉域邊界層網格和旋翼表面邊界層網格進行局部網格加密，并檢查Skewness等網格質量參數，保證網格質量和計算精度，最后對旋轉域網格和固定域網格進行拼裝。

本次仿真采用Realizablek-epsilon湍流模型，其適用于復雜幾何的外部流動問題，自由流過程模擬結果比標準模型的結果好，且在低雷諾數時的近壁面處理更加精確，魯棒性更高。選擇流體為不可壓縮，定義旋轉域旋轉坐標系和空氣計算域固定坐標系，網格類型分別為動網格、靜網格，并設置旋轉坐標系轉速(即旋翼轉速)。為有效模擬自由流，將固定域壁面邊界條件設為outflow、進出口邊界為壓力入口(pressure-inlet)和壓力出口(pressure-outlet)，設置旋翼表面邊界條件為無滑移的壁面(wall)，旋轉域與固定域接觸面邊界為內表面(interface)[6]。

圖1為旋翼流場在yOz平面速度矢量分布圖，觀察其流場分布，基本符合旋翼滑流理論中單旋翼流場的特性[7]。通過修正的動量葉素法對GWS6030×2型旋翼的拉力和阻力矩進行理論計算[8-9]，并與仿真結果進行對比來驗證此CFD仿真法所得結果可靠性。

圖1 轉速n=13 000 r/min旋翼流場速度矢量分布圖

懸浮彈擬重1 kg，對于多旋翼懸浮裝置的單個旋翼至少提供拉力分別為5 N(二旋翼)和2.5 N(四旋翼)。因此對GWS6030×2型旋翼在轉速為6 000～20 000 r/min區間內，進行拉力和阻力矩的仿真值與理論計算值進行對比。

圖2和圖3分別為GWS6030×2型旋翼拉力和阻力矩隨轉速變化的理論計算曲線與仿真值曲線。

圖2 GWS6030×2型旋翼拉力-轉速曲線

圖3 GWS6030×2型旋翼阻力矩-轉速曲線

觀察圖2和圖3可知，本文采用的流體仿真方法所得結果與理論計算曲線基本相符拉力和阻力矩隨轉速變化趨勢符合旋翼氣動特性規律[10]。在理論計算時，采用矩形槳葉旋翼進行計算簡化，而在仿真時用GWS6030×2型旋翼進行建模仿真。GWS6030×2型旋翼與矩形槳葉相比具有更好的氣動性能翼型，因此隨轉速增加，旋翼拉力仿真值較理論值高且具有較低的阻力矩，符合旋翼結構參數的氣動力影響規律[1]。

綜上所述，本文采用的CFD方法對GWS6030×2型旋翼流場及氣動力特性仿真準確性較高，可用于后文旋翼結構參數對翼間氣動干擾特性的影響研究。

3 多旋翼氣動干擾分析

旋翼流場的實質是耦合各干擾源及其下洗流的復雜流場，在該流場中旋翼產生下洗流的影響占主導地位，多個旋翼間下洗流將會產生干擾并導致復雜的干擾影響。因此旋翼間距將直接影響氣動干擾程度，進而影響到整個懸浮裝置的升力。本文利用前述CFD方法及GWS6030×2型旋翼模型，通過改變旋翼間距，求解不同間距下雙旋翼及四旋翼所提供升力，并與單旋翼升力無干擾疊加的結果進行比較，來分析旋翼間距對升力的影響。

GWS6030×2型旋翼槳葉數為k=2，螺距H=76.2 mm，槳葉直徑D=152.4 mm。由于三旋翼需額外平衡裝置抵消反旋扭矩，從而較多占用懸浮子彈體積與重量，且三旋翼翼間氣動干擾與二旋翼類似，故此處不予考慮。采用雙旋翼和四旋翼2種分布方式，為抵消反旋扭矩相鄰旋翼旋轉方向相反、對角旋翼旋轉方向相同。為提高普遍性，本文選取旋翼旋轉半徑R為基準，旋轉區間距變化區間為0.1R～1.5R,即旋轉軸間距L為2.1R～3.5R，次增量為0.1R進行仿真。

3.1 雙旋翼氣動干擾特性

對二旋翼進行幾何建模如圖4，圖中圓柱區域為旋翼旋轉計算域，L為旋翼間距。通過控制旋翼轉速不變，改變旋翼間距L，對旋翼進行仿真計算。

圖4 雙旋翼幾何模型及對應旋翼間距示意圖

考慮到懸浮子彈擬重(1 kg)情況和旋翼升力仿真結果與理論值準確度，由圖2可得在18 000 r/min時，單旋翼可提供拉力為5.45 N，故同樣選取雙旋翼轉速為18 000 r/min與單旋翼流場及氣動力進行分析。

圖5、圖6分別為雙旋翼在轉速n=18 000 r/min時的速度矢量圖和速度云圖。

觀察圖5及圖6可知：雙旋翼速度矢量圖和速度云圖與單旋翼相比，雙旋翼相鄰處上方來流氣體被旋翼拉扯分別吸入各個旋翼區域，且在各旋翼下洗流間存在復雜的相互干擾。旋翼下洗流區域呈現近端遠離、遠端相互誘導靠近的趨勢[10]。

圖5 轉速n=18 000 r/min雙旋翼速度矢量分布圖

圖6 轉速n=18 000 r/min雙旋翼速度云圖

圖7為旋翼轉速為n=18 000 r/min時，旋翼間距L=2.1R的雙旋翼與同轉速的單旋翼旋轉域上下表面壓強比較圖。觀察圖6、圖7可知，由于翼間氣動干擾，雙旋翼旋轉域上下表面壓差小于單旋翼。

圖7 n=18 000 r/min雙旋翼與單旋翼旋轉域壓強云圖

當雙旋翼間距L改變時，旋翼所提供總升力與單旋翼升力無干擾疊加(10.9 N)結果如圖8。

觀察圖8可知：當轉速保持不變時，隨著旋翼間距L的增加，雙旋翼總升力先增大后減小，最終趨向于穩定，此規律符合雙旋翼升力實驗[10]的變化趨勢，證明此次計算結果比較準確。當旋翼間距為2.1R時，雙旋翼損失的升力最大，與單旋翼升力無干擾疊加結果相比降低了約9.2%；當旋翼間距為2.8R左右時，總升力相比單旋翼略提高0.9%；當旋翼間距大于3.1R左右時，雙旋翼總升力與單旋翼升力無干擾疊加值基本相等。

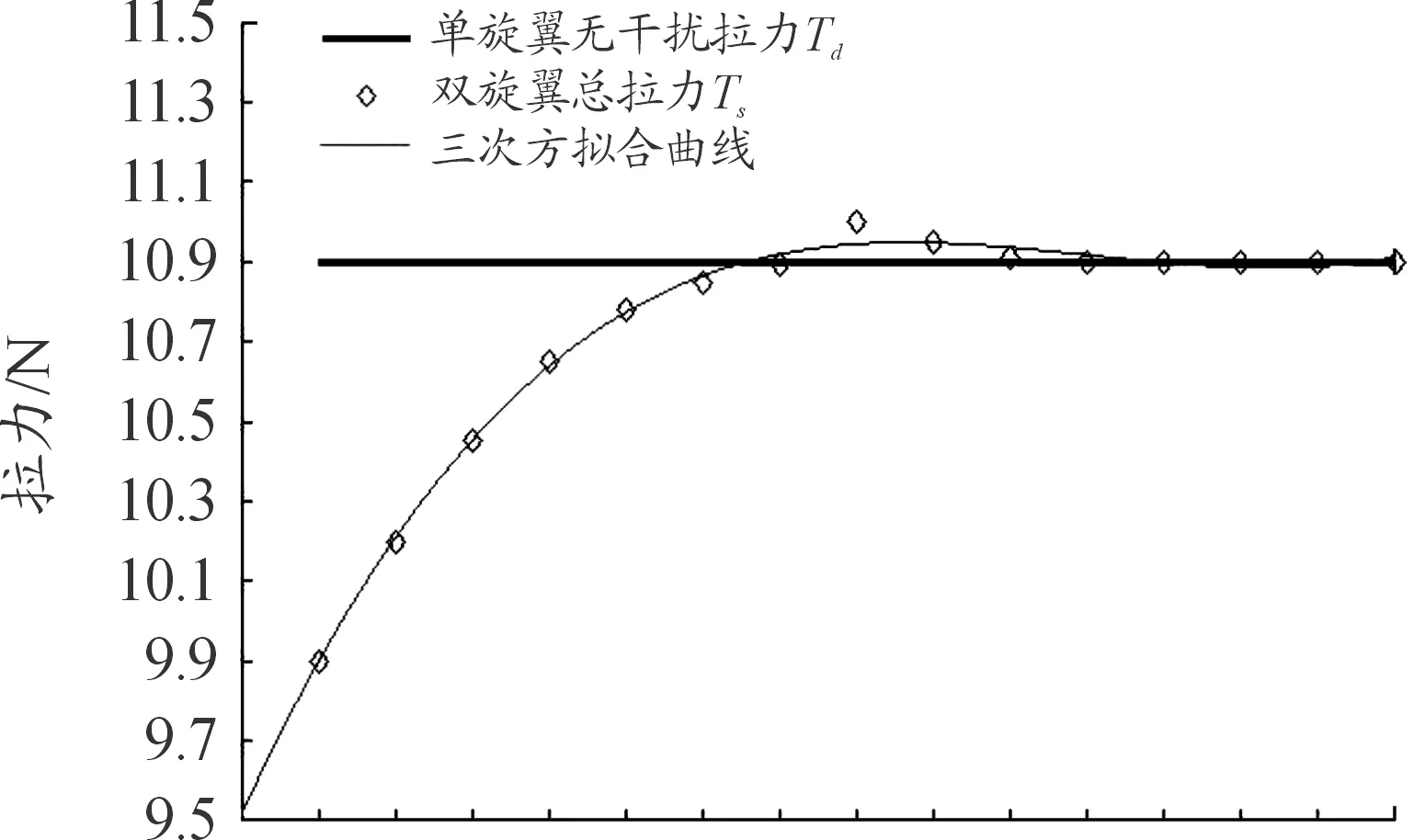
圖8 雙旋翼總拉力曲線

3.2 四旋翼氣動干擾特性

對四旋翼進行幾何建模如圖9。與雙旋翼不同，四旋翼的旋翼間距分為相鄰旋翼間距L和對角旋翼間距L′。旋翼間的氣動干擾不僅存在于相鄰旋翼之間，當相鄰旋翼間距L較小時，對角旋翼間同樣存在較為復雜的氣動干擾。

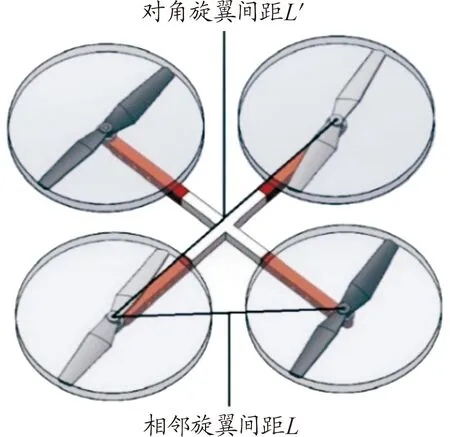
圖9 四旋翼幾何模型

同樣考慮懸浮彈重量及所需升力，由圖2可得在13 000 r/min時，單旋翼可提供拉力為2.71 N，故四旋翼轉速選為13 000 r/min進行對比分析。由于四旋翼的旋翼間相互干擾類似雙旋翼，故速度矢量圖選取新的參考平面進行觀察。如圖10為四旋翼下方5 mm處速度矢量分布圖。觀察圖可知：在間距較小時，四旋翼下洗流干擾不僅存在于相鄰旋翼，對角旋翼也同樣有下洗流間的干擾，各個旋翼受到3個干擾源，使得整個四旋翼流場更為復雜。

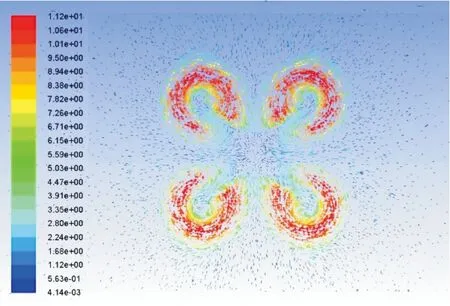
圖10 四旋翼下方5 mm處速度矢量分布圖

四旋翼成中心對稱分布，同樣通過控制相鄰旋翼間距L的變化，四旋翼總升力與單旋翼升力無干擾疊加(10.84 N)如圖11。

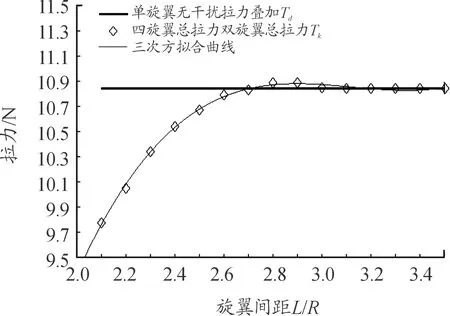
圖11 四旋翼總拉力曲線

觀察圖11可知：四旋翼間距變化對總升力影響的規律與雙旋翼基本相同。通過曲線擬合對雙旋翼和四旋翼總拉力疊加值進行擬合，其值變化規律都基本符合三次方擬合曲線，故多旋翼的總升力隨相鄰旋翼間距增大而先增大后減小，最終趨于穩定。當旋翼間距為2.1R時，四旋翼升力損失較大與單旋翼升力無干擾疊加結果相比降低了約10%，大于雙旋翼升力損失百分比(9.2%)；當旋翼間距為2.7R時，四旋翼總升力與單旋翼無干擾升力疊加基本相等，這與二旋翼特性相同；當旋翼間距為2.9R左右時，總升力相比單旋翼無干擾升力疊加值略提高0.8%；當旋翼間距大于3.1R左右時，四旋翼總升力與單旋翼升力無干擾疊加值基本相等。

由于“十”字分布式四旋翼，除兩兩相鄰旋翼間的流場干擾外，對角旋翼同樣存在流場間的相互干擾。因此當在較小旋翼間距時，對角旋翼間距同樣較小，從而導致升力損失系數比雙旋翼升力損失系數大很多。當旋翼間距在2.1R～2.7R區間內，隨著旋翼間距的增加，四旋翼升力損失系數與二旋翼升力損失系數的差值逐漸變小，說明四旋翼間除了相鄰旋翼間氣動干擾逐漸減弱的同時，對角旋翼間氣動干擾也逐漸變弱。當相鄰旋翼間距大于2.8R時，對角旋翼間距大于3.1R，則相互干擾影響可忽略不計,此時各旋翼僅受相鄰旋翼間的流場干擾，因此升力損失系數有所降低。而對于四旋翼“X”型分布，只需要考慮最近的相鄰旋翼間距，其他相鄰旋翼和對角旋翼間距值都較大，從而使得升力損失系數會有所降低。

4 結論

1) 對比GWS6030×2型旋翼的仿真結果和理論計算值，本文所采用的CFD仿真方法可以較準確地對小型旋翼進行數值仿真計算。

2) 在旋翼間的相互干擾下，旋翼下洗氣流區域呈現近端遠離、遠端相互誘導靠近的趨勢；相鄰旋翼上方來流氣流被分割，且氣流速度相對降低，單個旋翼上下表面間壓差變小，從而使得多旋翼總升力降低。

3) 以旋翼半徑R為基準,旋翼間距在2R～3.1R區間內，多旋翼升力相對單旋翼會存在不同程度地升力損失。在相同轉速下，當旋翼間距為2.1R～2.7R時，多旋翼的升力損失系數總體上隨著旋翼間距的增大而逐漸降低；當旋翼間距為2.7R～2.9R時，旋翼間氣動干擾相對較小，多旋翼總拉力略高于相應單旋翼無干擾拉力的疊加值；當旋翼間距大于3.1R時，旋翼間的氣動干擾對裝置懸浮能力影響可忽略不計。

4) 在相同間距和轉速下，旋翼的個數和分布方式也會影響懸浮裝置的升力損失系數。在相同轉速和間距情況下，四旋翼“X”型分布式較“十”字分布式升力損失較小“十”字分布式四旋翼比雙旋翼的升力損失系數更大。