基于構(gòu)造法的高中數(shù)學(xué)解題方法探討

段黽釗

(江蘇省南通市海門(mén)市包場(chǎng)高級(jí)中學(xué) 226100)

數(shù)學(xué)知識(shí)具有比較強(qiáng)的繁雜性與抽象性特性，是高中生學(xué)習(xí)的重點(diǎn)與難點(diǎn)所在，尤其是其中涉及到許多復(fù)雜性與綜合性比較強(qiáng)的類型題，常常使學(xué)生陷入解題困境.在正向解題思路下無(wú)法快速求解數(shù)學(xué)問(wèn)題，如果可以靈活地應(yīng)用逆向思維，借助構(gòu)造法分析問(wèn)題，那么就可以通過(guò)對(duì)題干中的隱性及顯性解題信息進(jìn)行挖掘來(lái)快速明確求解問(wèn)題所必備的關(guān)鍵解題條件與信息，進(jìn)而可以簡(jiǎn)化學(xué)生求解問(wèn)題的過(guò)程，提高了他們求解數(shù)學(xué)問(wèn)題的能力.

一、基于構(gòu)造方程法，求解數(shù)學(xué)問(wèn)題

構(gòu)造方程法是求解高中數(shù)學(xué)題中用的比較多一種解題方法，主要是由于方程和函數(shù)之間具有緊密聯(lián)系，許多數(shù)學(xué)類型題常常都可以通過(guò)尋求方程和函數(shù)之間的相關(guān)性來(lái)進(jìn)行求解.構(gòu)造方程法主要是在對(duì)相關(guān)問(wèn)題中的已知條件以及它們之間的相關(guān)性進(jìn)行深入分析的基礎(chǔ)上，通過(guò)利用這些已知關(guān)系與條件來(lái)相應(yīng)地構(gòu)造能夠求解問(wèn)題的等量方程.

例1已知(m-n)2-4(n-x)(x-m)=0，試求參數(shù)m，n，x之間互相構(gòu)成等差數(shù)列.

解析在求解這道與數(shù)列相關(guān)的類型題中，如果采用傳統(tǒng)求解方法，那么整體的求解難度比較大，并且還會(huì)使學(xué)生進(jìn)行大量的計(jì)算，容易造成錯(cuò)解情況.此時(shí)在求解這道問(wèn)題中可以靈活地運(yùn)用構(gòu)造法，以“參數(shù)m，n，x之間互相構(gòu)成等差數(shù)列”這一待求解條件作為求解問(wèn)題的已知條件，同(m-n)2-4(n-x)(x-m)=0這一給定的關(guān)系式相結(jié)合，那么可以具象化和簡(jiǎn)單化處理這道抽象數(shù)學(xué)問(wèn)題，大大提高了問(wèn)題求解效率.

解構(gòu)造如下方程：(m-n)t2-(m-n)t+(x-m)=0；

令F(t)=(n-x)t2+(m-n)t+(x-m).

通過(guò)分析本道題，可以發(fā)現(xiàn)：F(1)=0，可知：(n-x)t2+(m-n)t+(x-m)=0的實(shí)數(shù)根保持相等，求解可得：t=1，所以可知相應(yīng)方程實(shí)數(shù)根均為1.然后可以結(jié)合韋達(dá)定理來(lái)得到如下方程：m+n=2x，所以可知參數(shù)m，n，x之間互相構(gòu)成等差數(shù)列.

基于上述分析可知，在求解這道問(wèn)題中，核心解題思想是借助構(gòu)造法的運(yùn)用來(lái)簡(jiǎn)化復(fù)雜的問(wèn)題，提高問(wèn)題求解的準(zhǔn)確率與效率.

試求：tan(α+β+γ)的值.

解析針對(duì)上述這道涉及到三角函數(shù)的問(wèn)題，學(xué)生在求解的過(guò)程中如果直接采取分解待求函數(shù)tan(α+β+γ)的方式來(lái)求解問(wèn)題，那么會(huì)大大增加學(xué)生求解問(wèn)題的難度，并且非常容易出現(xiàn)錯(cuò)解情況.此時(shí)如果靈活應(yīng)用構(gòu)造方程的方法來(lái)簡(jiǎn)化問(wèn)題，那么可以大大提高解題的便捷性與準(zhǔn)確度，并且可以避免因?yàn)橛?jì)算量過(guò)大而造成錯(cuò)解情況的出現(xiàn).

解假定tanα=x，tanβ=y，tanγ=z,那么基于給定的題干條件可知，

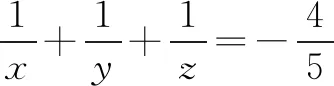
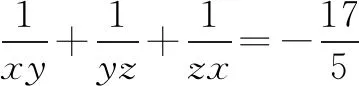
由此可見(jiàn)，靈活運(yùn)用構(gòu)造方程思想等一些方法來(lái)簡(jiǎn)化問(wèn)題求解過(guò)程，這樣可以最大程度提高學(xué)生求解數(shù)學(xué)問(wèn)題的質(zhì)量與效率.

二、基于構(gòu)造數(shù)列法，求解數(shù)學(xué)問(wèn)題

數(shù)列作為高中數(shù)學(xué)教學(xué)的重要內(nèi)容，是高考數(shù)學(xué)試卷必考的題目.其中主要涵蓋了等差數(shù)列、等比數(shù)列兩個(gè)方面的數(shù)列知識(shí)，但是卻依舊包含比較多的數(shù)學(xué)內(nèi)容.在求解數(shù)列問(wèn)題時(shí)，如果可以靈活地運(yùn)用構(gòu)造數(shù)列的方法，那么在求解部分?jǐn)?shù)學(xué)題目中常常會(huì)發(fā)揮非常神奇的效用，具體就是借助聯(lián)想或替換等方法來(lái)構(gòu)建等比數(shù)列或等差數(shù)列，之后結(jié)合數(shù)列方面的相關(guān)知識(shí)來(lái)深入分析題干當(dāng)中的相關(guān)信息、條件及要求，這樣可以極大地簡(jiǎn)化問(wèn)題，提高問(wèn)題分析及解決的有效性.

解析基于題干信息，給出部分解題條件與信息來(lái)求解Sn是一道比較常見(jiàn)的類型題.在明確前幾項(xiàng)之和，且給定了{(lán)an}這一通項(xiàng)公式，所以可以借此來(lái)推算出相應(yīng)的Sn表達(dá)式.

解基于問(wèn)題題干信息可得，在n≥2的時(shí)候，an=Sn-Sn+1，所以可知：

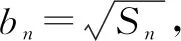
三、基于構(gòu)造函數(shù)法，求解數(shù)學(xué)問(wèn)題

同構(gòu)造方法這一解題方法類似，構(gòu)造函數(shù)法也是求解數(shù)學(xué)問(wèn)題中比較常見(jiàn)的一類解題方法，二者本質(zhì)在解題上存在相通性.在平時(shí)的解題教學(xué)中，可以結(jié)合具體的解題來(lái)指導(dǎo)學(xué)生同時(shí)訓(xùn)練自身靈活應(yīng)用構(gòu)造函數(shù)法求解數(shù)學(xué)問(wèn)題的能力.通過(guò)有效應(yīng)用構(gòu)造函數(shù)法分析及求解數(shù)學(xué)問(wèn)題，可以鍛煉學(xué)生思維的靈活性，尤其是在代數(shù)問(wèn)題、三角函數(shù)問(wèn)題、幾何問(wèn)題等相關(guān)數(shù)學(xué)類型題當(dāng)中.如果可以指導(dǎo)學(xué)生深入挖掘所給數(shù)學(xué)題目中的關(guān)鍵信息，找到其中有關(guān)的函數(shù)關(guān)系，那么可以將這些復(fù)雜數(shù)學(xué)問(wèn)題的求解過(guò)程進(jìn)行簡(jiǎn)化，配合函數(shù)問(wèn)題求解方法及思想的靈活應(yīng)用可以大大提高學(xué)生求解數(shù)學(xué)問(wèn)題的能力，同時(shí)借助構(gòu)造函數(shù)方法的靈活應(yīng)用可以進(jìn)一步提高整體的解題準(zhǔn)確率.

例4已知a,b,c,d均為實(shí)數(shù)，且滿足：針對(duì)任意一個(gè)實(shí)數(shù)x，均滿足下一不等式：acosx+bcos2x+ccos3x+dcos4x≤1.試求：a+b-c+d的最大值，以及此時(shí)a,b,c,d各自的值是多少？

解析在求解這一道三角函數(shù)相關(guān)的類型題中，由于其中涉及到a,b,c,d幾個(gè)未知參數(shù)，所以在對(duì)相應(yīng)不等式進(jìn)行化簡(jiǎn)的時(shí)候會(huì)遇到一些難題，學(xué)生常常不知道該如何解題.此時(shí)如果可以靈活應(yīng)用構(gòu)造函數(shù)法，那么可以將復(fù)雜的三角函數(shù)問(wèn)題進(jìn)行簡(jiǎn)化，快速找到解題的突破口，避免大量的計(jì)算.

解令f(x)=acosx+bcos2x+ccos3x+dcos4x

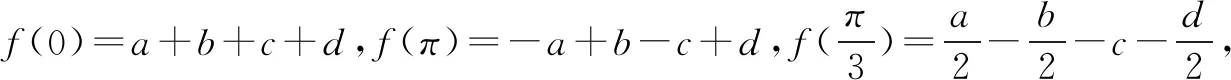
此時(shí)可以令t=cosx(-1≤t≤1)，那么可知:

f(x)-1=acosx+bcos2x+ccos3x+dcos4x-1

通過(guò)進(jìn)一步簡(jiǎn)化上式，可以得到：

f(x)-1=2(t-1)(t+1)(2t-1)[2dt-(1-d)]≤0

針對(duì)定義域?yàn)?-1≤t≤1)范圍內(nèi)的t，上式均成立，所以可知：d>0，且2d/2=(1-d)/1，求解得：d=1/2.這樣可以快速求解本道題的正確答案為：最大值為3，且對(duì)應(yīng)最大值時(shí)候a，b，c，d分別為1，1/2，-1和1/2.

綜上所述，在求解某些數(shù)學(xué)問(wèn)題中，如果可以指導(dǎo)學(xué)生巧用構(gòu)造法，通過(guò)構(gòu)造數(shù)列、構(gòu)造函數(shù)以及構(gòu)造方程，可以有效簡(jiǎn)化求解的問(wèn)題，大大提高學(xué)生解題的準(zhǔn)確度與效率.但是在實(shí)際求解問(wèn)題中應(yīng)用構(gòu)造法期間，必須要結(jié)合實(shí)際的類型題進(jìn)行合理分析，保證可以選擇適宜的構(gòu)造法來(lái)簡(jiǎn)化問(wèn)題，這樣才能不斷提升學(xué)生運(yùn)用構(gòu)造法解題的能力.