問題巧轉化 導數妙破解
——一道含參不等式恒成立問題的探究
2021-08-05 09:23:38李彥彥
數理化解題研究 2021年19期
關鍵詞:解決問題
李彥彥
(甘肅省酒泉市瓜州縣第一中學 736100)
不等式中的恒成立問題能夠很好地考查函數、不等式等知識以及化歸與轉化等數學思想,一直備受命題者青睞,是各級各類考試中的熱點問題之一.特別是涉及多個參數的不等式恒成立問題時,往往難度較大,讓人無從下手,而且此類問題有時表現比較隱蔽,不易分辨,切入點不易發現.而導數作為解決不等式恒成立問題的有效工具之一,可以很好地破解不等式中的恒成立問題.
一、問題呈現
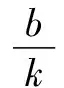
本題題目看似簡單,但參數較多,綜合含參數的一次函數與對數函數問題,不等式的恒成立以及代數關系式的最值問題等,內容豐富.如何通過含參不等式在定義域內的恒成立問題的轉化,進而得以確定兩相應參數k與b的比值的最值是解決問題的關鍵,而正確構造或轉化為相應的函數模型,利用導數方法來求解相應函數的最值是解決問題的突破口.
二、多解思維
思維角度1(構造函數轉化法1)根據題目條件,通過移項得到kx+b-ln(x+2)≥0,兩次把相應的不等式恒成立問題轉化為對應的函數的最值問題,通過求導,結合函數的單調性來確定其相應的最值,進而得到對應參數的比值的最小值.
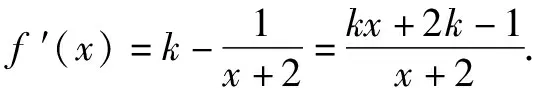
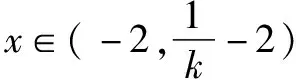
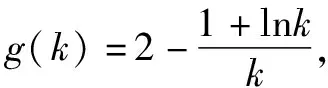
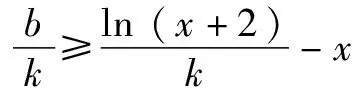
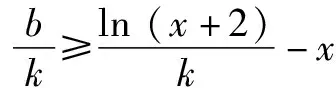
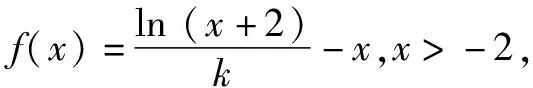
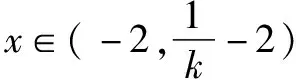
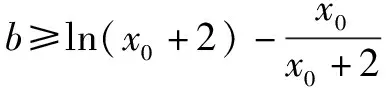
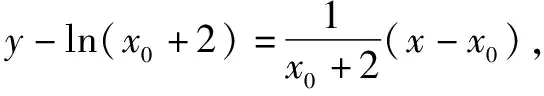
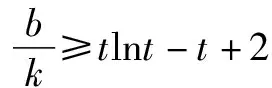
思維角度4(特殊值法)根據題目條件,由于kx+b≥ln(x+2)對于x>-2恒成立,通過選取特殊值x=-1代入對應的不等式,通過不等式的恒等變換得以確定k≤b,進而得到對應參數的比值的最小值.此類方法可以達到“秒殺”的功效,但方法不具有科學性,有一定的投機取巧之嫌.
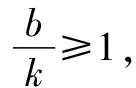
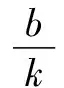
導數作為一種基本數學工具,可以用來處理與函數、不等式以及其他與之有關的很多問題,其中不等式的恒成立問題是其中最具有創新應用的一種.利用導數解決問題的實質是抓住用導數判斷函數單調性的應用來處理對應函數的單調性問題,從而再轉化為對應的不等式成立問題,巧妙轉化,綜合應用.
猜你喜歡
小學生學習指導(中年級)(2022年4期)2022-04-26 06:34:46
今日農業(2021年9期)2021-11-26 07:41:24
中學生數理化·七年級數學人教版(2021年10期)2021-11-22 07:53:00
數學小靈通·3-4年級(2021年9期)2021-10-12 05:47:28
數學小靈通(1-2年級)(2021年9期)2021-10-12 05:37:00
數學小靈通(1-2年級)(2021年6期)2021-07-16 05:20:58
數學小靈通(1-2年級)(2020年12期)2021-01-14 00:57:50
現代裝飾(2019年11期)2019-12-20 07:06:04
人大建設(2019年2期)2019-07-13 05:40:58
數學小靈通(1-2年級)(2017年12期)2018-01-23 03:37:01

