論類比思維下的高中數學解題方法
張 宇
(福建省福州延安中學 350001)
所謂類比思維是指根據兩個對象在某些屬性上相同或相似,通過比較而推斷出它們在其他屬性上也相同的推理過程.高中數學解題中,在類比思維指引下可使學生盡快找到解題思路,提高解題效率,因此要認識到類比思維的重要性,為學生講解類比思維在解題中的具體應用,使學生掌握相關的應用方法與技巧.
一、類比思維下方程習題的解答
眾所周知,函數與方程有著密切的聯系.對于無法直接求解方程根的習題,可通過轉化為函數圖象交點的問題進行突破.教學中為使學生掌握求解特殊方程根的方法,應結合學生所學知識,設計新穎的問題情境,鼓勵學生運用類比思維進行解答,使其在認識到類比思維的重要性的同時,進一步拓展其視野,積累求解方程根的新思路.
例1求“方程log2x+log3x=0的解”時,可設函數f(x)=log2x+log3x,則函數f(x)在(0,+∞)上單調遞增,且f(1)=0,因此原方程有唯一解x=1.類比上述思路,則方程(x-1)5+x-1=34的解集為____.
由于方程的根是對應函數與x軸交點的橫坐標,因此在解答該高次方程時需要從題干中得到啟示,進行合理類比,即先判斷對應函數的單調性,從整體上把握方程根的個數,而后結合自身經驗找到方程的根.該題難度并不大,解題思路可通過類比獲得,判斷高次函數單調性可借助導數進行分析.
根據給出的思路進行類比,令f(x)=(x-1)5+(x-1)-34,對其進行求導得到f′(x)=4(x-1)4+1,可知在x∈R上f′(x)>0,表明函數f(x)在x∈R上單調遞增,即f(x)和x軸只有一個交點,方程只有一個實根.又因為25+2=34,因此,x-1=2,解得x=3,則原方程的解集為{3}.
二、類比思維下幾何習題的解答
在平面幾何中有很多與立體幾何相類似的性質,在教學中可鼓勵學生認真思考,推導平面幾何中的一些性質是否在立體幾何中也適用.為激發學生探究的熱情,可從平面幾何結論入手自然引入立體幾何問題,要求學生運用類比思維進行分析、解答,親身感受類比的過程,積累運用類比思維解題的經驗.
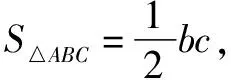
該題目以學生熟悉的平面幾何知識為切入點,要求其通過類比推導出立體幾何中的相關結論,既能鞏固學生所學,又能很好地鍛煉學生的類比推理能力.該題目給出的已知條件并不多,解答時應能透過現象看本質,大膽設出相關參數,運用所學進行嚴謹的推理.
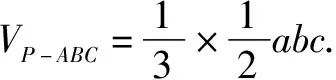
類比可知
VP-ABC=VO-ABC+VO-PAB+VO-PAC+VO-PBC
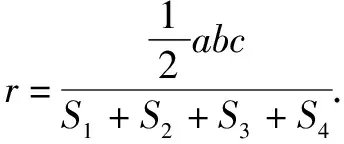
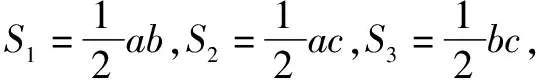
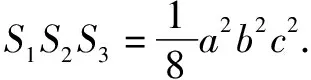
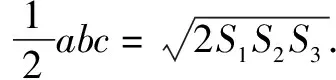
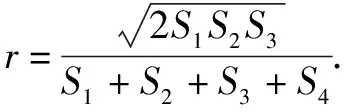
三、類比思維下數列習題的解答
數列是高中數學的難點知識,包括等差數列與等比數列,兩者之間有著類似的性質.因此,一些測試中常涉及兩者之間進行類比推理的習題,檢驗學生對數列知識的理解深度以及思維的靈活性.為了深化學生對數列知識的理解,掌握相關的解題方法,教學中應向學生展示一些經典習題,組織學生開展針對性訓練活動,鼓勵學生通過類比解答.
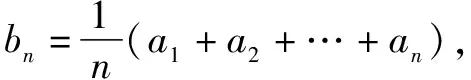
解題時要求認真分析已知條件中等差數列之和與項數之間的關系,吃透題意,把握其本質.如果學生不知如何下手,那么教學中可以引導學生先類比其“形”,猜想結論,必要情況下可代入特殊的數列進行驗證,若類比的結論正確,再運用所學知識進行證明.
為使學生能夠靈活運用類比思維正確解答相關數學習題,促進學生提升解題能力,教學中既要注重灌輸相關的理論,使學生把握類比的思路以及注意事項,又要圍繞例題,為學生做好解題示范,并鼓勵其做好聽課總結,真正消化、吸收所學,在解題中養成應用類比思維解題的習慣,不斷提高思維的靈活性,真正掌握這一重要的解題思維.

