多點思維 多點開花
——以2018年全國Ⅱ文第12題為例

劉美景

(江蘇省徐州市侯集高級中學 221121)

著名數學家蘇步青在《談談怎樣學好數學》中寫到：“正確地理解數學的基本概念之所以重要，是因為它是掌握數學基礎知識的前提.猶如造房屋那樣，基礎打得牢靠些，將來在它的上面造起來的房屋就不會坍毀.”在解決一些數學問題時，一定要充分理解數學的基本概念與基本性質，挖掘內涵，這才是解決問題的本質.2018年高考全國Ⅱ卷文科第12題中的函數問題，就是一道可以充分深挖內涵、巧妙拓展的好題.

一、真題在線

高考真題(2018·全國Ⅱ文·12，理·11)已知f(x)是定義域為(-∞，+∞)的奇函數，滿足f(1-x)=f(1+x).若f(1)=2，則f(1)+f(2)+f(3)+…+f(50)=( ).

A.-50 B.0 C.2 D.50

二、多向思維

結合抽象函數的基本性質與關系式，通過奇函數的性質、周期函數等來轉化與處理，可以直接利用函數的基本性質來切入，也可以借助特殊函數的引入來解決.

思維角度1(函數基本性質法1)

解法1 由于f(x)是奇函數，且滿足f(1-x)=f(1+x)，則有f(x+1)=f(1-x)=-f(x-1)，可得f(x+4)=-f(x+2)=f(x)，所以f(x)的周期為T=4.

結合f(x+1)=-f(x-1)，f(1)=2，可得f(3)=-f(1)=-2，而f(2)=f(-2)=-f(2)，可得f(2)=0，則有f(4)=-f(2)=0，則有f(1)+f(2)+f(3)+f(4)=0.

所以f(1)+f(2)+f(3)+…+f(50)=12×0+f(49)+f(50)=f(1)+f(2)=2，故選C.

思維角度2(函數基本性質法2)

解法2 由于f(x)是奇函數，且滿足f(1-x)=f(1+x)，則有f(x+1)=f(1-x)=-f(x-1)，可得f(x+4)=-f(x+2)=f(x)，所以f(x)的周期為T=4.

而f(x)是定義域為(-∞，+∞)的奇函數，則有f(0)=0.結合f(x+1)=-f(x-1)，f(1)=2，可得f(3)=-f(1)=-2，f(2)=-f(0)=0，則有f(1)+f(2)+f(3)+f(4)=0.

所以f(1)+f(2)+f(3)+…+f(50)=12×0+f(49)+f(50)=f(1)+f(2)=2，故選C.

思維角度3(特殊函數法1)

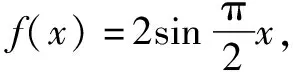
所以f(1)+f(2)+f(3)+…+f(50)=12×0+f(49)+f(50)=f(1)+f(2)=2，故選C.

三、拓展變式

通過深入分析該題，改變條件，拓展思維，可以得到意想不到的效果，真正達到“認真解答一個題，拓廣解決一類題，變式深化一片題，思維能力一起高”的美好目的.

變式方向1 改變條件，轉化求解代數式

變式1 已知f(x)是定義域為(-∞，+∞)的奇函數，滿足f(1-x)=f(1+x).若f(1)=2，則f(2018)+f(2019)=( ).

A.2018 B.-2 C.2 D.2019

解析由于f(x)是奇函數，且滿足f(1-x)=f(1+x)，則有f(x+1)=f(1-x)=-f(x-1)，可得f(x+4)=-f(x+2)=f(x)，所以f(x)的周期為T=4.

而f(x)是定義域為(-∞，+∞)的奇函數，則有f(0)=0，可得f(2018)=f(504×4+2)=f(2)=f(0)=0，f(2019)=f(505×4-1)=f(-1)=-f(1)=-2.

所以f(2018)+f(2019)=0-2=-2.故選B.

變式方向2改變條件，增加和式

變式2 已知f(x)是定義域為(-∞，+∞)的奇函數，滿足f(1-x)=f(1+x).若f(1)=2，則f(1)+f(2)+f(3)+…+f(2018)=( ).

A.-2018 B.0 C.2 D.2018

解析由于f(x)是奇函數，且滿足f(1-x)=f(1+x)，則有f(x+1)=f(1-x)=-f(x-1)，可得f(x+4)=-f(x+2)=f(x)，所以f(x)的周期為T=4.結合f(x+1)=-f(x-1)，f(1)=2，可得f(3)=-f(1)=-2，而f(2)=f(-2)=-f(2)，可得f(2)=0，則有f(4)=-f(2)=0，則有f(1)+f(2)+f(3)+f(4)=0.

所以f(1)+f(2)+f(3)+…+f(2018)=504×0+f(2017)+f(2018)=f(1)+f(2)=2，故選C.

變式方向3改變條件，給出給定區間的函數解析式

變式3 已知f(x)是定義域為(-∞，+∞)的奇函數，滿足f(1-x)=f(1+x).當x∈(0，1]時，f(x)=2x3，則f(1)+f(2)+f(3)+…+f(2018)=( ).

A.-2018 B.0 C.2 D.2018

解析由于f(x)是奇函數，且滿足f(1-x)=f(1+x)，則有f(x+1)=f(1-x)=-f(x-1)，可得f(x+4)=-f(x+2)=f(x)，所以f(x)的周期為T=4，而f(x)是定義域為(-∞，+∞)的奇函數，則有f(0)=0，而當x∈(0，1]時，f(x)=2x3，可得f(1)=2，結合f(x+1)=-f(x-1)，可得f(3)=-f(1)=-2，f(2)=-f(0)=0，則有f(1)+f(2)+f(3)+f(4)=0，所以f(1)+f(2)+f(3)+…+f(2018)=504×0+f(2017)+f(2018)=f(1)+f(2)=2，故選C.

變式方向4改變條件，增加三角函數內容

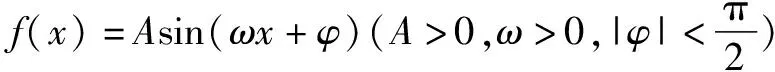
A.-2018 B.0 C.2 D.2018

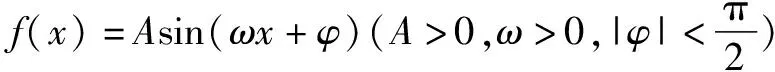
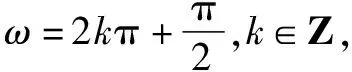
而f(1)+f(2)+f(3)+f(4)=2+0-2+0=0，所以f(1)+f(2)+f(3)+…+f(2018)=504×0+f(2017)+f(2018)=f(1)+f(2)=2，故選C.

羅增儒教授說過：“一旦獲解，就立即產生感情上的滿足，從而導致心理封閉，忽視解題后的再思考，恰好錯過了提高的機會，無異于入寶山而空返.”通過一題多解，一題多變等實踐，沒有停留在原有的解出題目的基礎上，而是解題后進行了變式探究.通過一題多變，培養學生的轉向機智及思維的應變性，實現提高發散思維的變通性.把課本練習題、考題等通過變換條件，變換結論，變換命題等，使之變為更有價值，有新意的新問題，從而應用更多的知識來解決問題，獲得“一題多練”“一題多得”的效果.