高考試題“充分與必要條件”歸類賞析
廖永福
(福建省廈門第二中學 361009)
判斷充分條件與必要條件,本質上就是判斷命題的真假,常用的方法有:
1.定義法:若p?q,則p是q的充分條件,q是p的必要條件;若p?q,則p是q的充要條件,q也是p的充要條件.口訣:箭尾充分,箭頭必要.
2.集合法:設A={x|x滿足條件p},B={x|x滿足條件q},若A?B,則p是q的充分條件,q是p的必要條件;若A=B,則p是q的充要條件.口訣:小充分,大必要,等充要.
3.等價法:應用等價的傳遞性,即“若p?q且q?r,則p?r”.
充分條件與必要條件涉及的知識面較廣,常與函數、三角函數、平面向量、數列、不等式和立體幾何等知識相結合.
一、以函數知識為載體
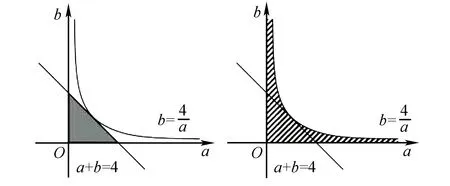
例1 (2020·上海卷)命題p:存在a∈R且a≠0,對于任意的x∈R,使得f(x+a) 命題q1:f(x)單調遞減且f(x)>0恒成立; 命題q2:f(x)單調遞增,存在x0<0使得f(x0)=0,則下列說法正確的是( ). A.只有q1是p的充分條件 B.只有q2是p的充分條件 C.q1,q2都是p的充分條件 D.q1,q2都不是p的充分條件 分析用定義法,只要判斷命題“若q1,則p”和命題“若q2,則p”的真假即可. 解析若q1成立,當a>0時,x+a>x,因為f(x)單調遞減且f(x)>0恒成立,所以f(a)>0,所以f(x+a) 綜上可知,q1,q2都是p的充分條件,故選C. 點評本題以函數知識為背景,主要考查充分條件的判斷,函數單調性的應用,考查推理和運算能力等,解題關鍵是把問題轉化為判斷兩個命題的真假,屬于中檔題. 變式1 (2016·上海卷)設函數y=f(x)的定義域為R,則“f(0)=0”是“函數f(x)為奇函數”的( ). A.充分而不必要條件B.必要而不充分條件 C.充分必要條件 D.既不充分也不必要條件 變式2 (2016·浙江卷)已知函數f(x)=x2+bx,則“b<0”是“f(f(x))的最小值與f(x)的最小值相等”的( ). A.充分不必要條件 B.必要不充分條件 C.充分必要條件 D.既不充分也不必要條件 答案:1.B 2.A 例2(2020·北京卷)已知α,β∈R,則“存在k∈Z使得α=kπ+(-1)kβ”是“sinα=sinβ”的( ). A.充分而不必要條件 B.必要而不充分條件 C.充分必要條件 D.既不充分也不必要條件 分析用定義法,并對k的奇偶性進行討論. 解答當k=2n(n∈Z)時,α=2nπ+β,此時sinα=sin(2nπ+β)=sinβ;當k=2n+1(n∈Z)時,α=2nπ+π-β,此時sinα=sin(π-β)=sinβ,即充分性成立. 若sinα=sinβ,則α=2nπ+β或α=2nπ+π-β(n∈Z),即α=kπ+(-1)kβ,即必要性成立. 所以,“存在k∈Z使得α=kπ+(-1)kβ”是“sinα=sinβ”的充要條件,故選C. 點評本題以三角函數知識為背景,主要考查充分條件和必要條件的判斷,考查誘導公式和三角函數性質的應用,考查分類討論思想等,解題關鍵是對k的奇偶性進行討論,屬于基礎題. 變式1 (2020·上海卷)“α=β”是“sin2α+cos2β=1”的( ). A.充分非必要條件 B.必要非充分條件 C.充要條件 D.既非充分又非必要條件 變式2 (2019·北京卷)設函數f(x)=cosx+bsinx(b為常數),則“b=0”是“f(x)為偶函數”的( ). A.充分而不必要條件 B.必要而不充分條件 C.充分必要條件 D.既不充分也不必要條件 答案:1.A 2.C A.充分而不必要條件 B.必要而不充分條件 C.充分必要條件 D.既不充分也不必要條件 分析用等價法,結合向量的減法公式和向量的運算法則即可作出判斷. 點評本題以向量知識為背景,主要考查充分條件和必要條件的判斷,考查平面向量的模、夾角與數量積,考查推理和運算能力等,解題關鍵是對題設條件進行等價轉化,屬于基礎題. 變式1 (2018·北京卷)設a,b均為單位向量,則“|a-3b|=|3a+b|”是“a⊥b”的( ). A.充分而不必要條件 B.必要而不充分條件 C.充分必要條件 D.既不充分也不必要條件 變式2 (2017·北京卷)設m,n為非零向量,則“存在負數λ,使得m=λn”是“m·n<0”的( ). A.充分而不必要條件 B.必要而不充分條件 C.充分必要條件 D.既不充分也不必要條件 答案:1.C 2.A 例4 (2016·天津卷)設{an}是首項為正數的等比數列,公比為q,則“q<0”是“對任意的正整數n,a2n-1+a2n<0”的( ). A.充要條件 B.充分而不必要條件 C.必要而不充分條件 D.既不充分也不必要條件 分析用集合法,先求出“q<0”和“對任意的正整數n,a2n-1+a2n<0”對應的集合,再根據兩個集合之間的包含關系作出判斷. 解答a2n-1+a2n=a1q2n-2(1+q),a1q2n-2>0.若對任意的正整數n,a2n-1+a2n<0,則1+q<0,解得q<-1. 因為“q<0”對應集合{q|q<0},“對任意的正整數n,a2n-1+a2n<0”對應集合{q|q<-1},且{q|q<0}{q|q<-1},所以“q<0”是“對任意的正整數n,a2n-1+a2n<0”的必要而不充分條件,故選C. 點評本題以數列知識為背景,主要考查充分條件和必要條件的判斷,考查等比數列的定義和性質,考查推理和運算能力,解題關鍵是把問題轉化為研究兩個集合之間的關系,屬于基礎題. 變式1 (2018·北京卷)設a,b,c,d是非零實數,則“ad=bc”是“a,b,c,d成等比數列”的( ). A.充分而不必要條件 B.必要而不充分條件 C.充分必要條件 D.既不充分也不必要條件 變式2 (2018·上海卷)設Sn為數列{an}的前n項和,“{an}是遞增數列”是“{Sn}是遞增數列”的( ). A.充分非必要條件B.必要非充分條件 C.充要條件 D.既非充分又非必要條件 變式3 (2017·上海卷)已知a,b,c為實常數,數列{xn}的通項xn=an2+bn+c,n∈N*,則“存在k∈N*,使得x100+k,x200+k,x300+k成等差數列”的一個必要條件是( ). A.a≥0 B.b≤0 C.c=0 D.a-2b+c=0 答案:1.B 2.D 3.A 例5 (2019·浙江卷)若a>0,b>0,則“a+b≤4”是“ab≤4”的( ). A.充分不必要條件 B.必要不充分條件 C.充分必要條件 D.既不充分也不必要條件 分析若用定義法,只要判斷命題“若a>0,b>0,a+b≤4,則ab≤4”和“若a>0,b>0,ab≤4,則a+b≤4”的真假即可;若用集合法,則應先求出“a>0,b>0,a+b≤4”和“a>0,b>0,ab≤4”對應的集合,再確定它們之間的包含關系,最后得出結論. 所以“a+b≤4”是“ab≤4”的充分不必要條件,故選A. 解法2集合M={(a,b)|a>0,b>0,a+b≤4}表示的平面區域為圖1中的陰影部分,集合M={(a,b)|a>0,b>0,ab≤4}表示的平面區域為圖2中的陰影部分. 圖1 圖2 由此可見MN,所以“a+b≤4”是“ab≤4”的充分不必要條件,故選A. 點評本題以不等式知識為背景,主要考查充分條件和必要條件的判斷,考查基本不等式的應用,考查推理與計算能力等,解題關鍵是把問題轉化為判斷兩個命題的真假或判斷兩個集合之間的關系,屬于基礎題. 變式1 (2020·天津卷)設a∈R,則“a>1”是“a2>a”的( ). A.充分不必要條件 B.必要不充分條件 C.充要條件 D.既不充分也不必要條件 變式2 (2019·天津卷)設x∈R,則“x2-5x<0”是“|x-1|<1”的( ). A.充分而不必要條件 B.必要而不充分條件 C.充要條件 D.既不充分也不必要條件 A.充分非必要條件 B.必要非充分條件 C.充要條件 D.既非充分又非必要條件 A.必要不充分條件 B.充分不必要條件 C.充要條件 D.既不充分也不必要條件 答案:1.A 2.B 3.A 4.A 例6 (2019·全國Ⅱ卷)設α,β為兩個平面,則α∥β的充要條件是( ). A.α內有無數條直線與β平行 B.α內有兩條相交直線與β平行 C.α,β平行于同一條直線 D.α,β垂直于同一平面 分析用定義法,結合面面平行的判定定理和性質定理可得結論. 解析對于A,α內有無數條直線與β平行,α∩β或α∥β;對于B,α內有兩條相交直線與β平行,α∥β;對于C,α,β平行于同一條直線,α∩β或α∥β;對于D,α,β垂直于同一平面,α∩β或α∥β.故選B. 點評本題以立體幾何知識為背景,主要考查充分條件和必要條件的判斷,考查面面平行的判定和性質,考查邏輯推理能力,屬于基礎題. 變式1 (2020·浙江)已知空間中不過同一點的三條直線l,m,n.則“l,m,n共面”是“l,m,n兩兩相交”的( ). A.充分不必要條件 B.必要不充分條件 C.充分必要條件 D.既不充分也不必要條件 變式2 (2018·浙江卷)已知平面α,直線m,n滿足m?α,n?α,則“m∥n”是“m∥α”的( ). A.充分不必要條件 B.必要不充分條件 C.充分必要條件 D.既不充分也不必要條件 變式3 (2016·山東卷)已知直線a,b分別在兩個不同的平面α,β內,則“直線a和直線b相交”是“平面α和平面β相交”的( ). A.充分不必要條件 B.必要不充分條件 C.充要條件 D.既不充分也不必要條件 答案:1.B 2.A 3.A二、以三角函數知識為載體
三、以平面向量知識為載體

四、以數列知識為載體
五、以不等式知識為載體
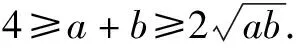
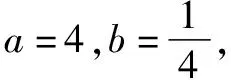
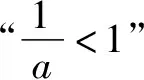
六、以立體幾何知識為載體

