計及網絡重構的主動配電網供電能力概率評估

李沛然，袁旭峰，趙 真，簡 力，熊 煒，鄒曉松

（貴州大學 電氣工程學院，貴州 貴陽 550025）

0 引言

供電能力是反映配電網安全性和經濟性的重要指標，指滿足一系列約束條件下配電網可以輸送的最大功率，主動配電網（active distribution network，ADN）由于其主動控制特性和分布式電源（distributed generation，DG）的加入使供電能力的評估方式和尺度發生了變化，因此準確評估主動配電網的供電能力就成為急需解決的問題。

主動配電網相比于傳統配電網的一個優勢在于可采取對系統中“源–荷–網–儲”協同控制方式[1]。主動配電網對配電網資源的主動決策管理和控制，通過對各元素的控制和網端靈活重構，實現電網高質量運行。近幾年也有一些文獻對含DG的配電網供電能力進行研究。文獻[2]改進了重復潮流法，求取各種方案下網絡每小時的供電能力，建立了一系列指標，并用德爾菲法綜合評估各項指標，但該文獻的風光出力以及評估權重過于單一。文獻[3]通過對風光出力的不確定性構造盲數模型，實現含DG的供電能力評估，但對于風光的盲數設置缺乏實際的支持。文獻[4]提出一種多目標直流配電網供電能力模型，利用智能算法對不同接線形式下的風光接入情況下的供電能力進行求解，研究了滲透率與供電能力的相關性。文獻[5]針對風光出力以及線路故障的隨機性生成場景，對主動配電網短期的供電能力進行評估。文獻[6]運用兩點估計法計算含DG配電網的最大供電能力分布，得出全局和不同區域下的供電能力分布函數。文獻[7]模擬了 DG及負荷的變化過程，并以此為依據進行供電能力的評估。文獻[8]在安全性的基礎上又考慮了用戶的需求，在雙重約束下評估配電網的供電能力。文獻[9]通過半不變量法處理DG的不確定性，對含DG的配電網進行供電能力評估。

以上文獻對主動配電網的供電能力進行了一定程度的研究，但只在單一的運行方式下評估配電網供電能力的結果偏向保守，不符合主動配電網的主動控制特性和發展趨勢[10-15]。因此主動配電網供電能力的評估需要以網絡重構為基礎，通過重構優化得到最有利于主動配電網供電能力的網架結構[16]。針對電網的隨機性，本文建立了新的供電能力評價指標體系，選擇適合評估供電能力的概率潮流計算方法，重點分析 DG接入前后與不同運行方式下配電網供電能力產生差異的原因，并以供電能力的期望為目標函數找到主動配電網最大的供電能力運行方式，為主動配電網的日常運行提供參考。

1 ADN供電能力評估指標

本文將主動配電網供電能力定義為在滿足約束條件的前提下，網絡能攜帶最大負載的能力PNSC（network supply capacity，NSC），目標函數如式（1）[17]：

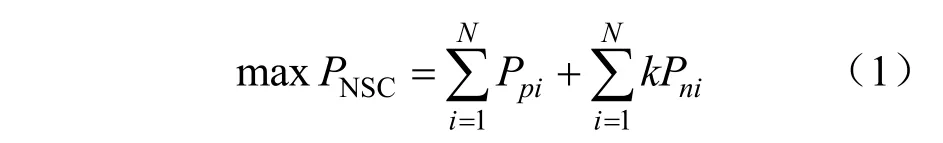
式中：PNSC表示滿足約束條件下主動配電網的供電能力；Ppi表示i節點的初始負荷；Pni表示i節點基準負荷；k表示i節點基準負荷的增長倍數，n表示網絡節點數。

PNSC求解過程如下：所有節點的基礎負荷值按照一定比例不斷增長，如果負荷越限則返回前一次數值，減小k的數值繼續讓負荷增長，最終達到最大值。本文將k達到最大值時的PNSC作為電網供電能力。

由于DG出力的不確定性，配電網供電能力不再是一個確定性的值，下面利用一系列新的指標來評價主動配電網的供電能力。

（1）供電能力期望ENSC

反映DG隨機出力的情況下配電網能達到的平均供電功率，供電能力期望ENSC可表示為：

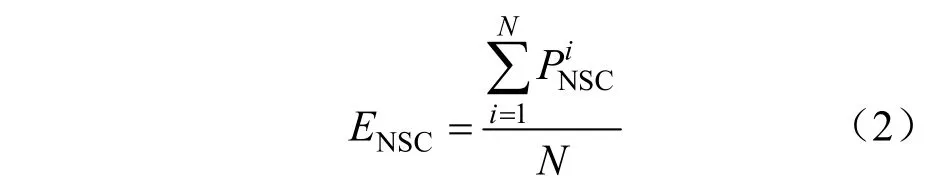
式中：N表示蒙特卡羅隨機抽樣次數；PiNSC表示第i次抽樣所對應的供電功率。

（2）供電能力標準差Dz

該指標表示的是抽樣下每個PNSC的均勻程度，具體公式表示如下：

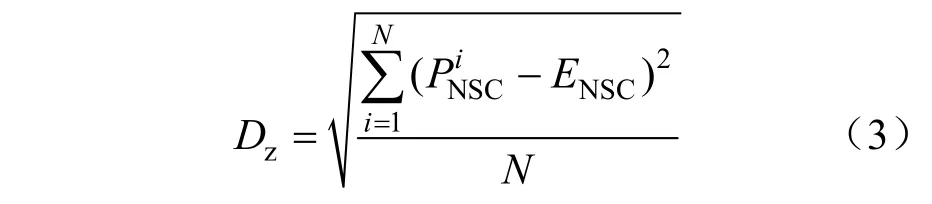
（3）供電能力峰值Pmax

該值指的是經過N次抽樣后樣本中能輸送的最大供電功率，由統計學規律可知如果樣本在[ENSC–3Dz,ENSC+3Dz]區間內，樣本的覆蓋率為99.7%，故可以將樣本中供電能力峰值定義如下[18]：

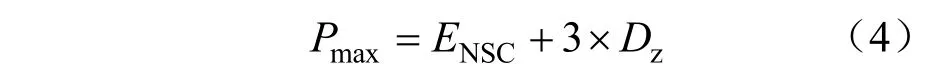
（4）供電能力谷值Pmin

該值指的是經過N次抽樣后樣本中能輸送的最小供電功率：

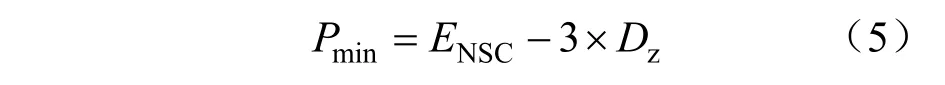
（5）變異系數c

變異系數，用來比較均值顯著不同樣本之間的離散狀態，具體計算公式如下：

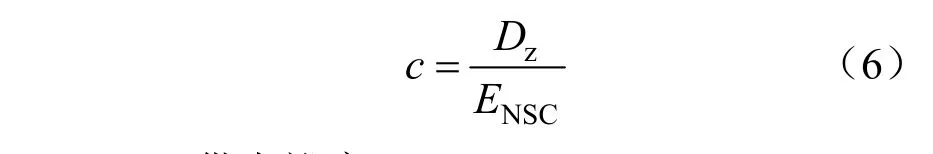
（6）供電裕度η

供電裕度反映的是主動配電網除開當前負荷后攜帶負荷的能力，公式如下：

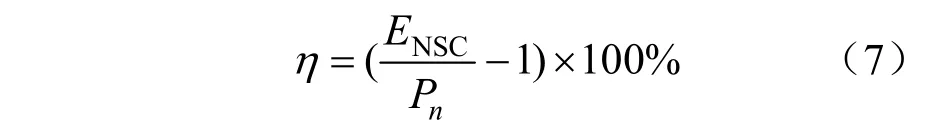
2 ADN供電能力概率評估

2.1 DG及負荷數學模型

由于主動配電網中 DG出力及負荷波動具有不確定性，分別用概率分布函數模擬各元素[19-20]。

風速服從Weibull分布，公式如下：

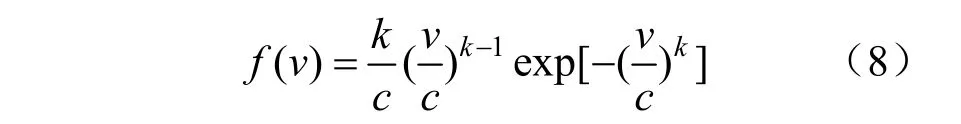
式中：k和c表示形狀和尺度參數。

風速是風機出力的決定性因素，風力發電的功率與風速的具體函數如下所示：

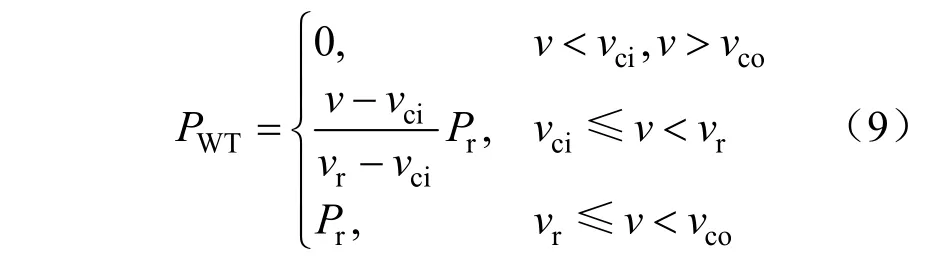
式中：vci和vco為切入、切出風速，vr和v分別為額定與實際風速，Pr和PWT為風機額定功率、輸出功率。

光伏出力符合Beta分布，公式如下：

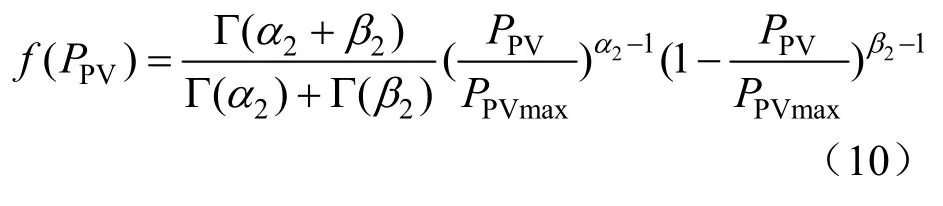
α2和β2表達式如下：

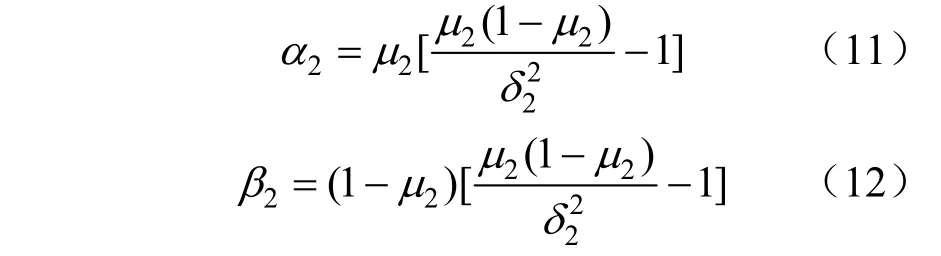
式中：μ2和σ2為光照強度均值標準差。

考慮到主動配電網中存在大量可中斷負荷和可轉移負荷，設負荷服從正態分布N(PN,σ)。PN和σ為均值及標準差[21]。

2.2 ADN供電能力概率評估

若評估對象為含有k個隨機變量的主動配電網，每個隨機變量需要估計出3個樣本點進行計算，根據概率統計理論，配電網中所有DG以及負荷構造的樣本點離散分布的前k階矩與待求隨機變量的前k階矩相等，通過對離散點前k階矩求解，計算出概率密度函數。構造配電網中每個隨機變量對應的樣本點，每個分量的計算方式如下：

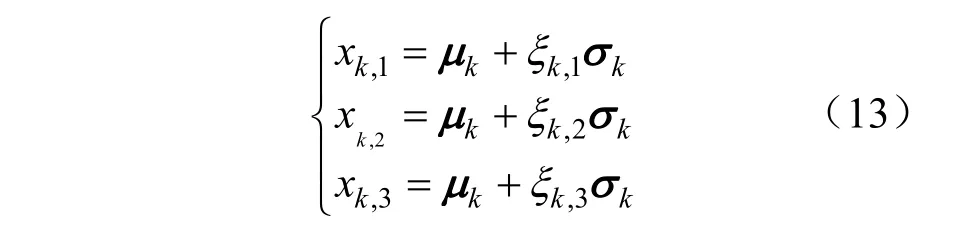
式中：μk是X的一階原點矩；σk是xk的標準差；xk,1，xk,2，xk,3分別是X的第k個隨機變量估計點；ξk,1，ξk,2，ξk,3是每個樣本點對應的位置參數。

樣本點權重與位置參數的關系如下：

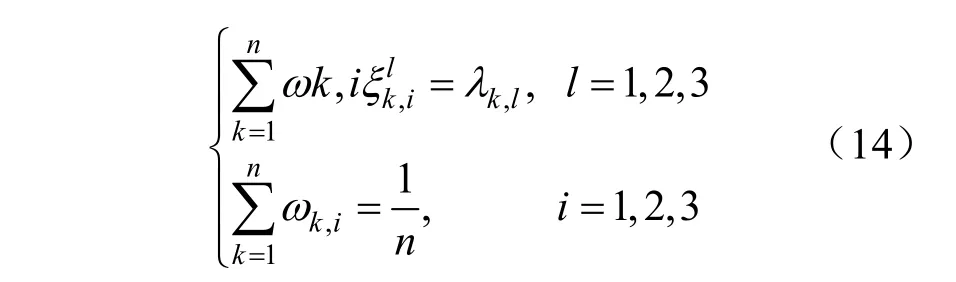
式中：λk,l表示l階中心距Ml(xk)與σk的l次方的比值，即：

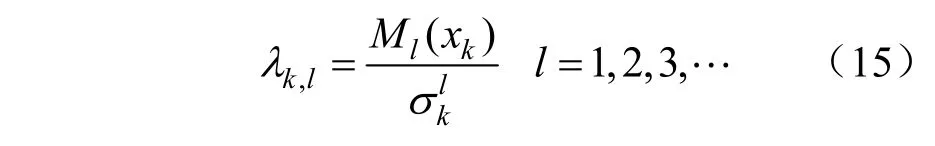
式子中λl,l=0；λ2,l=1；λ3,l為xk的偏度，表示的是相對于正態分布該分布函數的偏差；λ4,l為xk的峰度，表示的是分布函數在平均值附近的斜率情況。

配電網中含有的隨機變量可以利用點估計法通過式（12）的3個樣本點及其對應的位置參數與權重轉化為確定性計算。

約束條件具體公式如下所示：

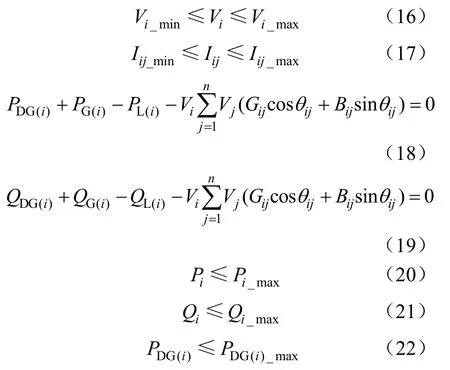
式中：Vi表示i節點電壓；Iij表示支路電流；Vi_min、Vi_max、Iij_min、Iij_max分別為其約束上下限。PG(i)和QG(i)表示i節點發出有功、無功；PL(i)和QL(i)表示i節點有功、無功負荷；Gij、Bij、θij分別表示i與j間的電導、電納、相角；Pi和Qi表示i節點變壓器有功、無功容量；Pi_max和Qi_max為其上限。PDG(i)表示i節點DG發出功率，PDG(i)max為其輸出功率上限。

最大功率分布具體計算流程如圖1所示：

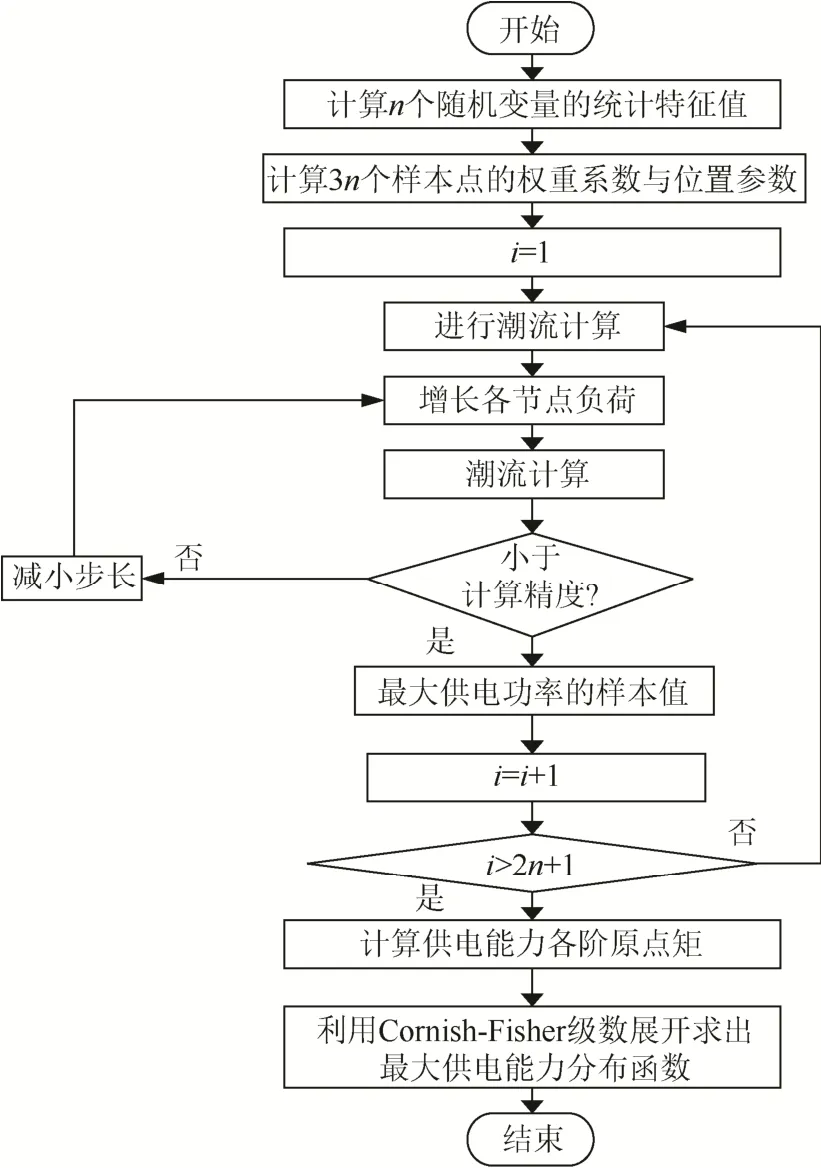
圖1 主動配電網供電能力概率評估流程圖Fig. 1 Flow chart of probabilistic evaluation of power supply capacity of active distribution network

步驟1：輸入電網的原始參數，給定各個節點的初始基準負荷有功Ppi，若含有n個隨機變量，運用三點估計法分別取出3n個樣本進行計算。

步驟2：設定每個節點的增長有功負荷Pni以及負荷增長步長k，同時給定計算精度e。

步驟3：增大負荷帶入網絡計算，判斷是否滿足約束條件，若不滿足進行步驟4，若滿足繼續增大負荷。

步驟4：用P=Ppi–kPni作為下一次潮流計算的各節點實際負荷。

步驟5：判斷k是否比計算精度小，若k大于e，實施步驟6，若k小于e，實施步驟7。

步驟6：縮短步長k，讓負荷的增長步長從k變為k=k/2返回步驟5，若不滿足計算精度，則先令P=Ppi–kPni，需要返回步驟3繼續迭代。

步驟7：計算結束后得出每個隨機變量對應的3個樣本點的供電功率，并利用式（14）求出供電功率的統計特征值λi,l。

根據半不變量的數學性質，可以計算出供電能力統計量的前t階原點矩，公式如下：

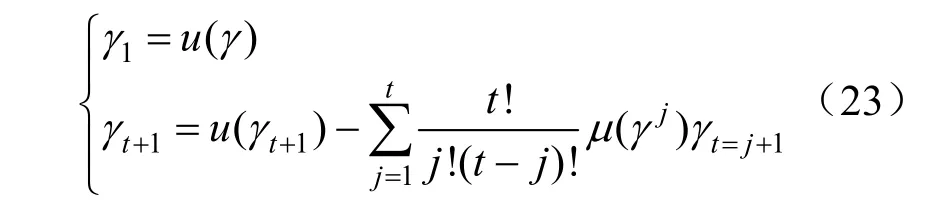
式中：γt+1表示t+1 階半不變量，t=1,2,…

利用 Cornish-Fisher展開公式求取隨機變量的概率密度y(φ)，φ為供電功率y分位數，近似表示為：

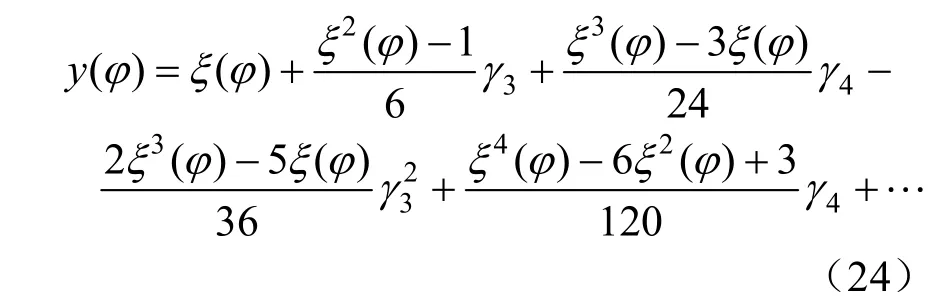
式中：ξ(φ)=Ф–1(φ)，Ф表示標準正態分布N（0,1）

利用y(φ)=F–1(φ) 的性質，可以計算出供電能力y的概率分布函數F(φ)。

按照上述流程，首先根據各隨機變量的中心矩，計算出估計點的位置參數及相應權重，根據計算后的值，利用重復潮流法求出網絡供電能力的樣本值和各階矩，采用Cornish-Fisher級數將計算出的供電能力樣本值和各階中心矩展開，求出供電能力的分布和概率密度函數。

3 計及配網重構的主動配電網供電能力優化

3.1 目標函數與約束條件

目標函數設為ADN中供電能力期望最大，具體表述如下式：

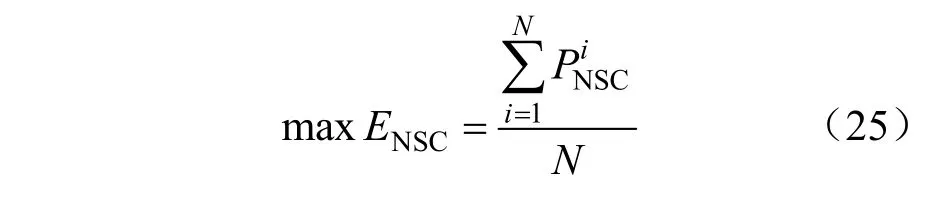
約束條件除了式（15）～（20）中的網絡約束外，考慮DG出力的隨機性約束條件式（21）改為下式[22]：

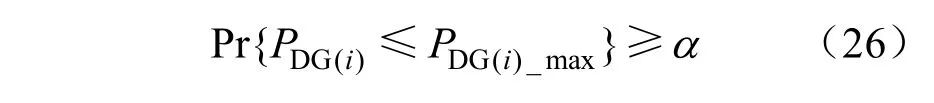
式中：α為預設的置信度，設定為0.95。

此外還需考慮配電網的網絡結構約束，保障配電網輻射狀運行，公式如下：

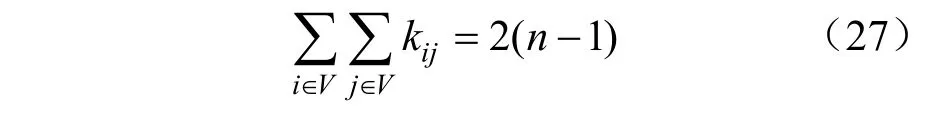
式中：i,j表示節點編號；V表示網絡節點集合；n表示配電網節點數。

3.2 求解方法

本文運用二進制粒子群算法（binary particle swarm optimization，BPSO）計算配網重構，提升配電網的供電能力[23]。二進制粒子群算法更新速度和粒子位置可以用下式表示：

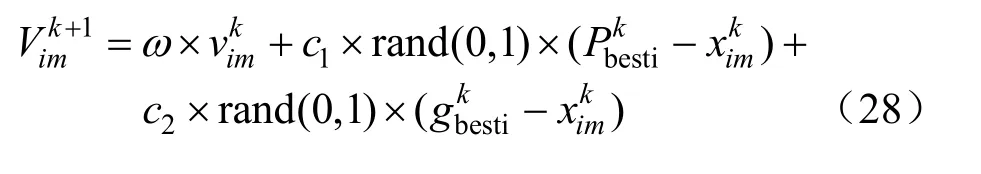
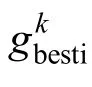
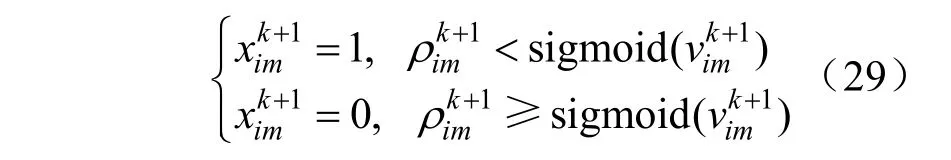
式中：ρ表示在[0,1]內產生的隨機數。

sigmoid函數表述如下：

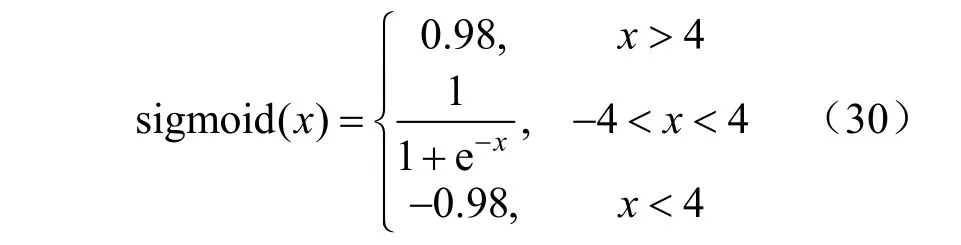
通過不斷調整搜索過程中ω的值，使開始計算時搜索的解空間較大，算法后期可以縮小區域精準搜索加快收斂，更新權重ω的公式如下：

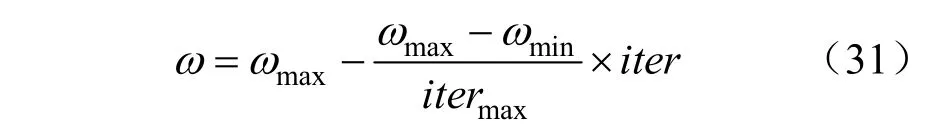
式中：ω表示權重系數，ωmax和ωmin分別是其最大最小值；iter表示當前迭代次數，itermax表示迭代次數上限。

基于配網重構的供電能力評估具體的求解流程如圖2所示。

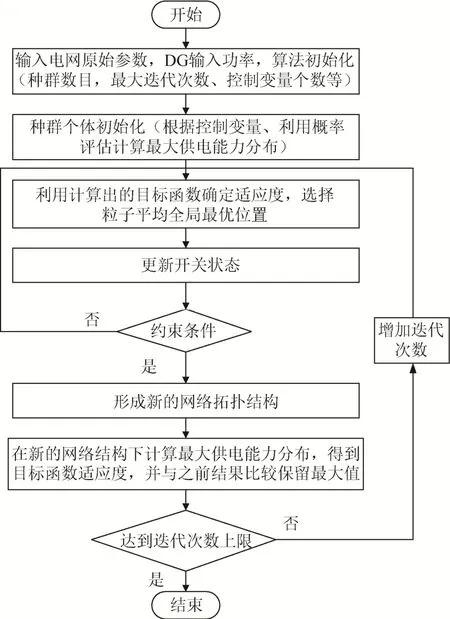
圖2 基于BPSO的供電能力配網重構流程圖Fig. 2 Flow chart of reconfiguration for power supply capacity distribution network based on BPSO

具體計算步驟如下：

步驟1：輸入種群數目，最大迭代次數，電網的初始數據，網絡開關的開斷信息，以及控制變量的個數。

步驟2：根據初始的開關狀態，確定當前的運行方式，利用上一節計算方法得到當前供電能力的分布函數期望值，計算粒子適應度。

步驟3：計算出粒子的全局最優位置，更新開關狀態后，計算當前運行方式是否滿足一系列約束條件。

步驟4：若滿足約束條件則形成新的網絡拓撲結構，若不滿足回到步驟3。

步驟5：計算新網絡下的供電能力期望值，得到適應度函數，并保留最大值。

步驟6：判斷是否達到迭代上限，若達到輸出結果，若沒有返回步驟3。

步驟7：計算結束，輸出優化后的配電網拓撲結構與對應的供電能力分布。

4 算例分析

4.1 算例模型

算例模型選取PG & E69節點配電網，如圖3所示，電網初始負荷為4.38+j2.1 MVA，在電網節點33、37、52處加入風電，最大出力400 kW，在25、67、41處加入光伏，最大出力300 kW，風電和光伏的控制策略采取恒功率因數方式運行[24-25]。DG參數見表1、表2。

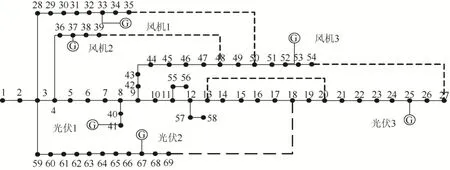
圖3 算例模型Fig. 3 Example model

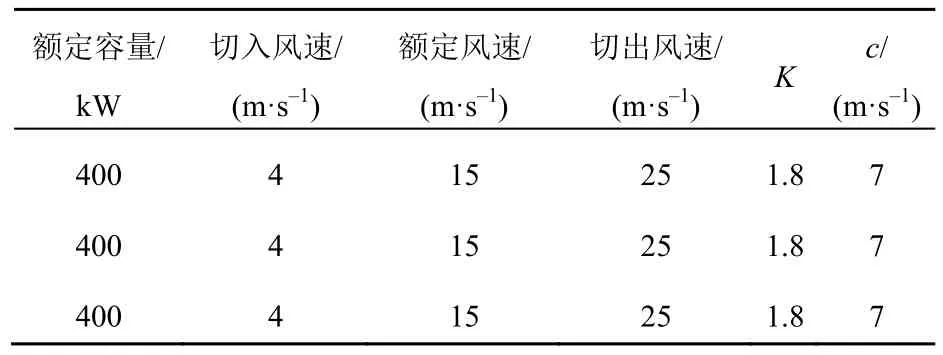
表1 風機參數Tab. 1 Fan parameters

表2 光伏發電的相關參數Tab. 2 Relevant parameters of photovoltaic power generation

4.2 算例1

算例1直接計算原始網絡的供電功率分布，采用三點估計法（three point estimation method，3PEM）與蒙特卡洛法（monte carlo solution，MCS）（n=1 000）進行對比[26]。計算結果如表3所示：

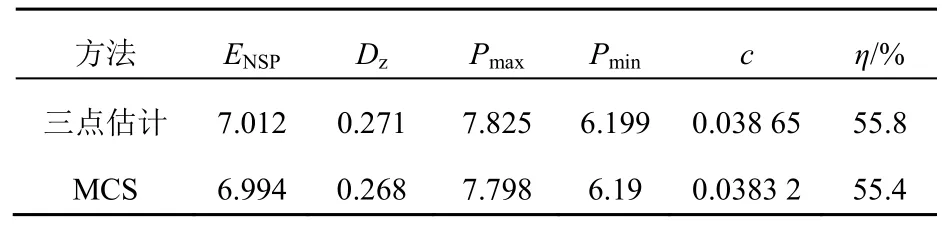
表3 算例1下配電網供電能力指標（MW）Tab. 3 Power supply capacity index of distribution network under example 1

從結果來看 MCS與本文所用三點估計法計算出的供電能力的分布函數重合度較高，MCS計算得出的ENSP為7.012 MW標準差為0.271，三點估計法計算得出的ENSP為6.994 MW，標準差為0.268，驗證了本文所提方法能夠有效地計算出主動配電網供電功率的分布函數。同時由于重構前負荷分布不均勻，故而電網的供電裕度只有55.8%，電網沒有得到充分的利用。

4.3 算例2

算例2運用二進制粒子群算法計算出最優的運行方式，在確定網架下用蒙特卡洛法（n=1 000）進行對比，如圖4所示。

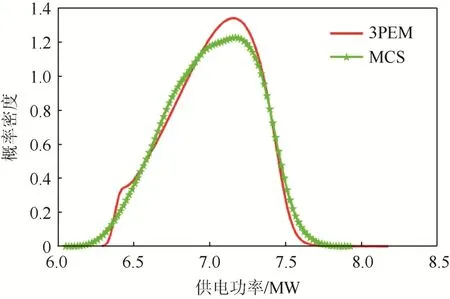
圖4 兩種方法得出的最大功率分布函數Fig. 4 Maximum power distribution functions obtained by the two methods

算例2重構優化得到的主動配電網網架結構如圖5所示。

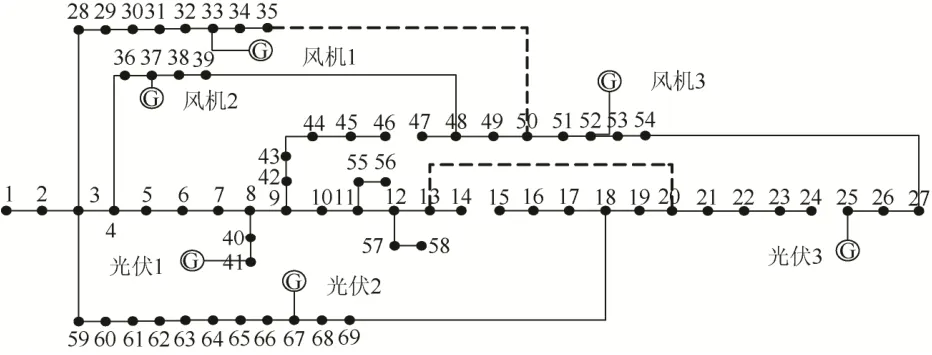
圖5 重構后的主動配電網結構圖Fig. 5 Structure diagram of active distribution network after reconfiguration

表4 重構開關動作Tab. 4 Switch actions of reconfiguration

進行重構優化后，在確定網架下用蒙特卡洛法（n=1 000）進行對比，計算結果如表5所示。

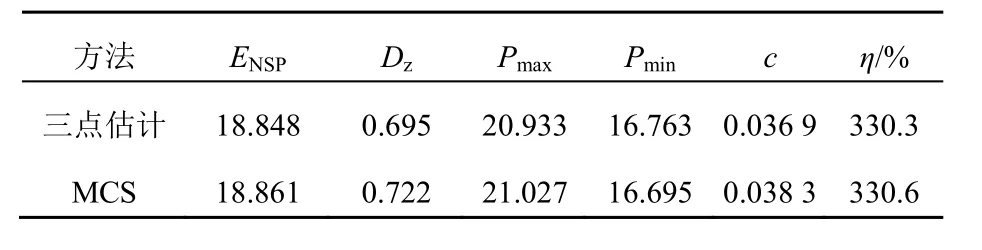
表5 算例2配電網供電能力指標（MW）Tab. 5 Indexes of power supply capacity of distribution network in example 2

通過對算例1和算例2的主動配電網供電能力分布函數比較可知，經過配網重構后供電能力值大幅度提升，重構前網絡的供電功率期望ENSP為7.12 MW，通過重構得出的網絡結構供電功率的期望為ENSP為18.84 MW，供電裕度也從重構前的55.8%增加到了重構后的330.3%，這都說明通過靈活改變運行方式可以提升配電網的供電能力。主動配電網供電功率的標準差從重構前的0.271增大到了重構后的0.695，說明主動配電網供電功率增大的同時供電能力的波動性也隨之增大。

4.4 算例3

算例3為了說明DG接入對供電能力的作用，在算例2的重構后的網架下針對不同的DG接入配電網的情況計算相應的供電能力，具體情況如圖6、表6、圖7、表7所示。

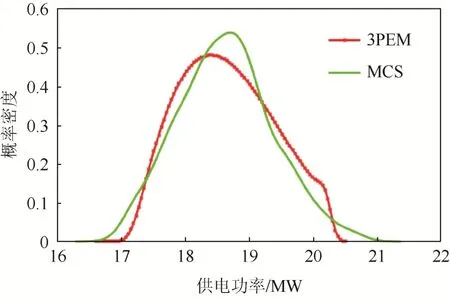
圖6 重構后兩種方法得出的最大功率分布函數Fig. 6 Maximum power distribution functions obtained by the two methods after reconfiguration

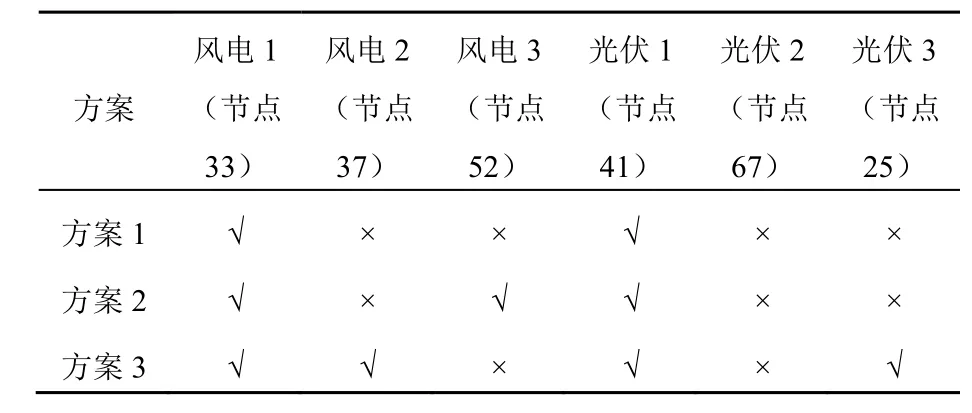
表6 不同接入方案描述Tab. 6 Description of different access schemes

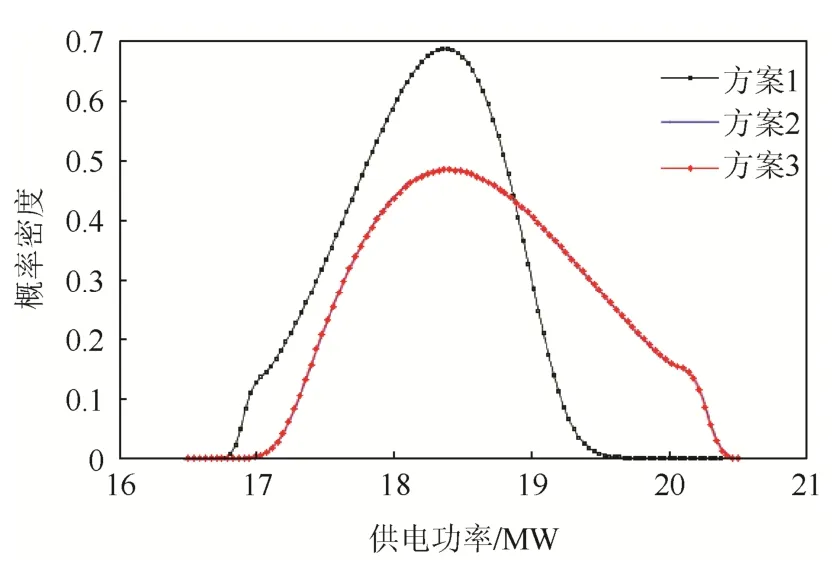
圖7 不同方案下的最大功率分布函數Fig. 7 Maximum power distribution functions under different schemes

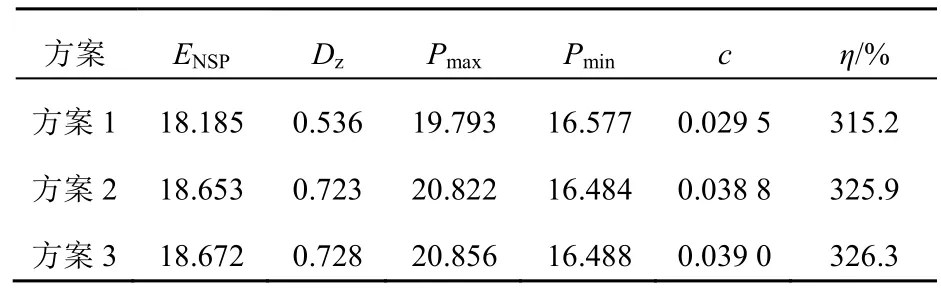
表7 算例3不同方案下的配電網供電能力指標（MW）Tab. 7 Indexes of power supply capacity of distribution network under different schemes

方案1～方案3的供電能力分別為：18.18 MW、18.65 MW和18.67 MW，供電裕度分別為315.2%、325.9%、326.3%，隨著DG的增多電網整體的ENSP也相應增大，并且相應的供電能力標準差Dz也在不斷增大，分別為0.536、0.723、0.728。

5 結論

為綜合評估主動配電網的供電能力，本文分析了源、網、荷3方面對主動配電網供電能力的影響，首先提出評價主動配電網供電能力的新指標，其次通過三點估計法與重復潮流法相結合，運用Cornish-Fisher級數把樣本點的各階半不變量展開得到電網的供電能力分布函數，與MCS計算出的供電能力分布函數比較，證明方法的有效性。最后以分布函數的期望為目標函數，運用二進制粒子群算法計算出最有利于供電能力的運行方式。由實驗結果看出DG的加入提升電網供電能力的同時也增大了供電能力的波動。而重構前后的供電能力各項指標對比可以發現運用網絡重構能夠大幅度提升主動配電網的供電能力與供電裕度。