基于結構參數分級優化的電機電磁噪聲抑制

羅玉濤 盧若皓

（華南理工大學機械與汽車工程學院 廣州 510000）

0 引言

車用驅動電機噪聲問題由于受到輕量化、高速化、高轉矩密度化等電機技術發展趨勢影響而愈發明顯，已經成為評價驅動電機性能乃至整車性能的關鍵指標[1-3]。電機噪聲包括空氣動力噪聲、機械傳遞噪聲及電磁振動噪聲。其中，電磁振動噪聲相較于前兩種噪聲，幅值更高，更易引起人體不適且抑制更為困難[4-5]。

電機電磁噪聲的直接抑制常通過優化電機結構參數的方法入手。對于定子結構參數的優化，D.Torregrossa等[6]以定子齒寬、齒深以及斜槽度為優化對象，通過解析分析其與定子模態頻率的關系確定最優定子結構參數，從而避免發生共振。李巖等[7]分析了定子齒削角與聲壓級之間的關系，并通過有限元法比較了四種齒削角下的聲壓級水平，從而確定最佳齒削角的大小。轉子參數的優化方面，T.Ishikawa等[8]以永磁體的排列位置參數為優化對象，以降低電磁振動并保證輸出轉矩不降低為優化目標，通過響應面法確定永磁體的最佳位置。

通過優化徑向電磁力密度與電磁轉矩波動以間接抑制電磁噪聲的方法同樣受到關注。文獻[9-12]指出，徑向電磁力密度與切向電磁轉矩的波動水平是電磁噪聲水平的重要表征，并對其進行了解析推導與驗證。王凱等[13]對優化徑向電磁力和切向轉矩波動所需關注的結構參數進行總結，包括斜槽角、定子槽形、極弧系數、磁鋼形狀等。優化實例方面，王曉遠等[14]對轉子隔磁橋的形狀進行改進，在保證不降低轉子強度的前提下降低徑向電磁力的幅值，從而對電磁噪聲進行抑制。鮑曉華等[15]解析了轉子磁極輔助槽對轉矩波動的影響，并通過枚舉法確定能最大限度地降低轉矩波動的輔助槽槽形。左曙光等[16]對氣隙電磁力密度進行解析推導，以峰值最小為優化目標，基于敏感性分析結果確定了定子槽形、磁鋼尺寸與氣隙大小的優化值，其團隊后續還建立了外轉子永磁電機的電磁-結構-聲學模型，仿真和實驗表明，齒槽效應引起的電磁力對噪聲影響最為顯著，在對槽口寬進行優化后電磁噪聲得以抑制[17]。

基于上述內容可以看出，電磁噪聲的直接抑制與間接抑制都需要對電機的結構參數進行優化，同時優化過程需解決的關鍵問題在于不犧牲電機輸出性能的前提下如何對繁多的結構參數進行有序、有效和高效的優化。針對該問題，本文選用以徑向電磁力密度峰值最小、轉矩波動比例最小以及切向電磁轉矩均值最大為優化目標的間接電磁噪聲抑制方法；采用基于多項式擬合的關鍵系數計算結構參數敏感性；對結構參數進行篩選并分為強敏感性、中敏感性、弱敏感性三級；綜合多目標遺傳算法、響應面法以及下降單純形法對結構參數進行分級優化；通過結構聲學仿真驗證電磁噪聲強度抑制及聲品質改善的效果。

1 徑向電磁力與電磁轉矩模型

優化目標選擇原因為：①徑向電磁力密度與切向電磁轉矩的波動水平與電磁噪聲水平直接關聯[9-12]；②對徑向電磁力密度與切向電磁轉矩波動進行優化，能夠對電磁噪聲產生較好的抑制效果[13-17]；③由于直接抑制過程為多物理場耦合計算，間接抑制過程為電磁場獨立計算，因此前者對計算機處理能力有更高的要求，在同樣計算能力下前者計算效率低于后者。

基于以上三點，本文采用間接抑制電磁噪聲的方法，選擇以徑向電磁力密度的峰值最小、切向電磁轉矩波動最小為本文主要優化目標，同時以切向電磁轉矩平均值最大為約束，從而避免以過度犧牲輸出能力為代價抑制電磁噪聲。以下對徑向電磁力密度與切向電磁轉矩求解模型進行說明。

1.1 徑向電磁力密度模型

電機空載時，氣隙磁場b1(t,θ)全部由轉子永磁體建立，等于氣隙磁導λ(t,θ)與氣隙磁動勢l(t,θ)的乘積[16]，有

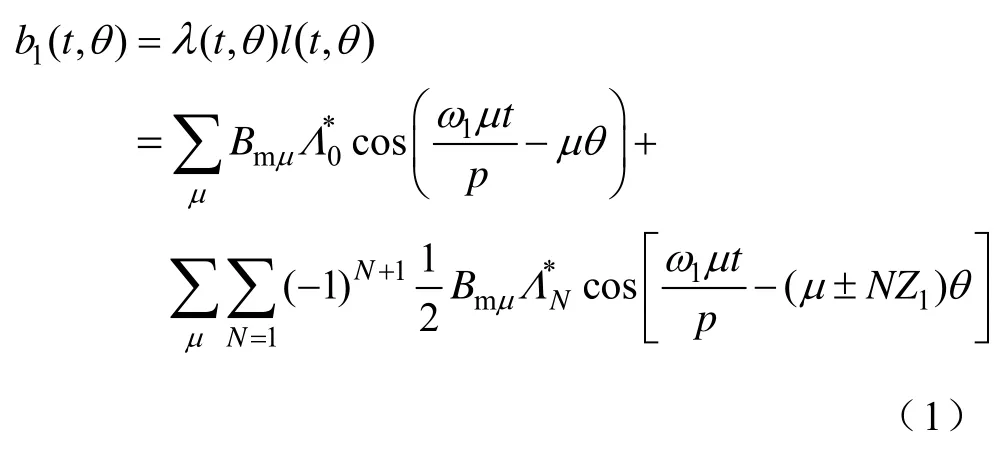
式中，Z1為齒數；t為時間；θ為空間機械角；Bmμ為轉子徑向磁場Bm第μ次諧波的幅值；*0Λ為恒定磁導分量；*NΛ為在定子開槽，轉子光滑時的磁導分量，N為正整數；ω1為轉動頻率；p為極對數。其中，μ滿足

式中，r為正整數，r= 0 ,1,2,3,…。

繞組通入三相正弦電流的負載工況下，氣隙磁場增加定子繞組產生的徑向磁場分量b2(t,θ)為

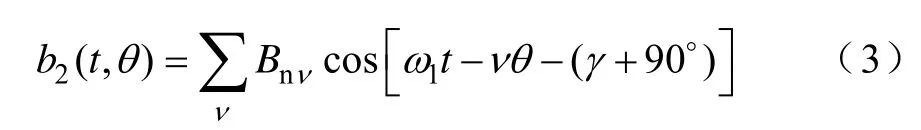
其中

式中，Bnv為定子徑向磁場Bn第ν次定子徑向磁場諧波幅值；γ為定子繞組電流的相位；k為正整數，k= 0 ,1,2,3,…。

此時負載工況下的氣隙磁場等于空載氣隙磁場b1(t,θ)與繞組電流磁場b2(t,θ)的和，有

根據Maxwell應力張量法，永磁電機徑向電磁力密度f(t,)θ為

式中，0μ為真空磁導率。

將式（5）代入式（6），在展開中略去與時間無關，僅產生靜變形的常態力以及高階次低幅值力[18]，由此得到對電磁噪聲影響較大的徑向電磁力密度模型為

式中，Bm、Bn下角標的數字表示諧波次數。

式（7）由四項組成，可以分為兩類：第一類為定子主波磁場或轉子主波磁場單獨作用下產生的力波（此時μ=ν=p= 2 ），對應第Ⅰ、Ⅲ項。其磁場幅值最大，產生的力波幅值也最大，是強烈電磁噪聲的重要激勵；第二類為空載工況下轉子第μ次諧波磁場和轉子主波磁場勵磁下定子1次諧波磁場相互作用產生的力波，以及負載工況下定子齒諧波磁場（ν=Z1?p= 2 2，k=2）與轉子第μ次諧波磁場作用產生的力波，分別對應第Ⅱ、Ⅳ項。該類力波除幅值較高外，組成成分還包含引起強烈電磁噪聲的零階呼吸力波（μ=22時的力波）。

在氣隙中心圓周對f(t,θ)進行積分，其中，圓周半徑為

式中，Rairgap為氣隙中心圓弧半徑；Ristator為定子內徑；dr為氣隙長度。因此徑向電磁力密度沿氣隙中心圓弧的分布為

結構參數通過影響磁場強弱來影響F(t,)θ的峰值，而F(t,)θ的峰值直接影響結構聲學響應的強弱[16,19]，因此，將F(t,)θ的峰值p(t,)θ最小作為優化目標，p(t,)θ為

1.2 切向電磁轉矩模型

由于有限元求解器可直接求解切向電磁力波的平均值，無需定義其求解式，在下文中以Tavg(t)表示，以數值最大為優化目標。轉矩波動比例則按式（11）進行計算，以絕對值最小為優化目標。Tmax(t)、Tmin(t)分別為輸出轉矩的最大、最小值，有

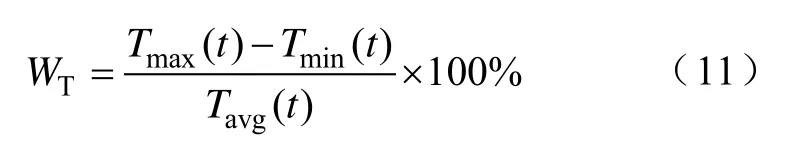
至此完成優化目標p(t,)θ、Tavg(t)、WT模型定義。

2 電機結構參數的分級優化

2.1 電機基本參數

本文研究對象為一臺24槽4極表貼式永磁同步電機，其橫截面如圖1所示，電機工作參數與基本結構參數見表1。為實現在給定電流幅值下輸出最大轉矩，通過參數化掃描確定A相激勵電流初相位。

表1 電機工作參數與基本結構參數Tab.1 Motor operating parameters and basic structural parameters

圖1 待優化電機橫截面Fig.1 The cross section of motor which will be optimized

本文的優化原則為：在盡可能不對電機基本尺寸進行修改的前提下對電機其余結構參數進行優化，從而降低電驅動系統整體關于電磁噪聲抑制的設計成本。待優化結構參數按照參數來源分為定子結構參數、轉子結構參數以及裝配參數。定子結構參數為槽形參數，包括槽口寬Bs0、槽心寬Bs1、槽底寬Bs2、槽底圓角半徑Rs、槽口高Hs0、槽寬高Hs2；轉子結構參數為永磁體形狀參數，包括極弧系數Emb以及厚度Thi；定、轉子結構參數如圖2所示。

圖2 定、轉子結構參數Fig.2 The structural parameters of stator and rotor

裝配參數為定子連續斜槽總斜度Ske以及氣隙大小dr，其中，dr變化時定子內徑不變，轉子外徑變化。上述10個結構參數的初始值與變化范圍見表2。

表2 結構參數初始值與變化范圍Tab.2 Initial value and range of structure parameters

結構參數的變化范圍以不造成模型干涉為原則，盡量包含所有的可能取值進行確定。

2.2 結構參數的敏感性分析

首先對結構參數進行敏感性分析，并根據結構參數對優化目標的影響程度對結構參數進行篩選與分級。敏感性分析流程如圖3所示。

圖3 敏感性分析流程Fig.3 The process of sensitivity analysis

2.2.1 參數樣本空間采樣與樣本點求解

共10個結構參數參與分析，若采用全空間均勻掃描法，每個參數取 10個樣本點，則需采集 1010個樣本點，后續計算量龐大。為保證敏感性分析精度的同時降低計算量，采用基于蒙特卡洛抽樣的進階拉丁超立方抽樣法（Advanced Latin Hypercube Sampling, ALHS）進行抽樣。

該方法適用于參數數量小于50的敏感性分析，通過引入隨機進化策略，最小化參數之間的無關聯系對后續敏感性分析結果的影響，因此在小容量樣本的情形下仍可獲得較為精確的敏感性分析結果[20-21]。對于10個結構參數及其變化范圍組成的樣本空間共采集500個樣本，相比全空間掃描法大大減少了后續敏感性分析計算量。

完成采集后，將樣本點導入有限元求解器并計算對應的p(t,)θ、Tavg(t)與WT，求解時間設為2個電周期共5ms，步長為0.05ms。

2.2.2 結構參數對優化目標影響程度

在同樣的抽樣方法下，常用的基于方差的敏感性分析相較于基于關鍵系數的敏感性分析需要更大數量的樣本[22]；同時由于后續響應面優化同樣需要進行2次多項式擬合，考慮方法的計算效率以及平臺延續性，采用基于多項式擬合的關鍵系數表征結構參數對優化目標的敏感性水平。

基于所采集的樣本以及對應的求解結果，擬合目標函數y(Xi)對待分析參數Xi多項式回歸方程為

式中，pT(Xi)為關于結構參數的多項式，有

式中，β為多項式的系數行列式；iε為擬合誤差。多項式最高次數為2次的原因在于，雖然2次多項式無法精確描述多個敏感性不同的設計參數與優化目標之間的關系，但對于敏感性分析而言，2次多項式已經可以獲得較為理想的分析結果[23-24]，同時計算量也可控制在較為合適的范圍內。

進一步可基于擬合方程計算判定系數R2，有

式中，yi為樣本目標實際值；μy為樣本目標均值；為y(xi)對應計算值；M為樣本數。

為避免過擬合情況的影響，對判定系數進行修正，有

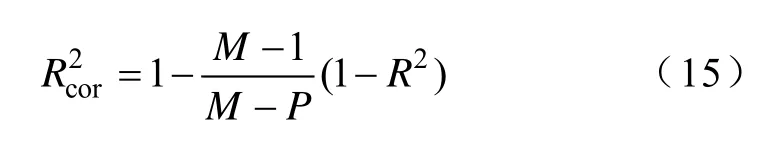
式中，P為所擬合多項式的系數的數量。基于判定系數可以計算待分析參數Xi對目標Yi的關鍵系數（Coefficient of Importance, CoI），有

式中，被減項表示包含所有結構參數的全擬合模型的決定系數；減項表示去除結構參數Xi的線性項、二次項以及相互作用項后的擬合模型的決定系數；二者的差值即表示去除該結構參數后擬合模型的變化情況，因此，CoI(Xi,Yi)數值越高，結構參數Xi相對于優化目標Xi的敏感性越高。計算結果見表3。

表3中，總體結構參數的CoI是指對某一優化目標產生影響的所有結構參數的關鍵系數。根據結構參數的敏感性分析結果，可以得出以下結論：

表3 結構參數敏感性計算結果Tab.3 Results of sensitivity calculation of structural parameters

（1）總體結構參數對3個優化目標的CoI均在90%以上，說明優化目標和與其有關的結構參數間存在較強的相關性。

（2）Emb、Thi、dr與Ske對 3個優化目標中的一個或多個產生超過20%的影響，因此，將這4個結構參數的敏感性等級設為強敏感級。

（3）Bs0、Hs0主要對p(t,)θ產生影響，且影響水平在8%以上；Bs1對Tavg(t)、p(t,)θ產生影響，但其主要影響p(t,)θ，對Tavg(t)影響較小，因此，將這3個結構參數敏感性等級設為中敏感級。

（4）Bs2、Hs2主要對切向電磁轉矩平均值Tavg(t)產生影響，影響水平分別為3.9%和4.2%，在5%以下。因此，將這兩個結構參數的敏感性等級確定為低敏感級。

（5）槽底圓角半徑Rs為與優化目標無關的結構參數，被過濾，不參與下一階段的優化計算，待優化結構參數數量減少為9個。

2.3 結構參數的分級優化與優化全局性判斷流程

基于上述參數敏感性分級結果，對每一級參數采用與其數量、影響優化目標的數量以及影響水平相適應的優化方法，降低每級優化計算量的同時實現對每個參數的深度優化，優化中的激勵電流為表1中的激勵電流，對應額定轉速下輸出額定轉矩工況。結構參數分級優化流程如圖4所示。

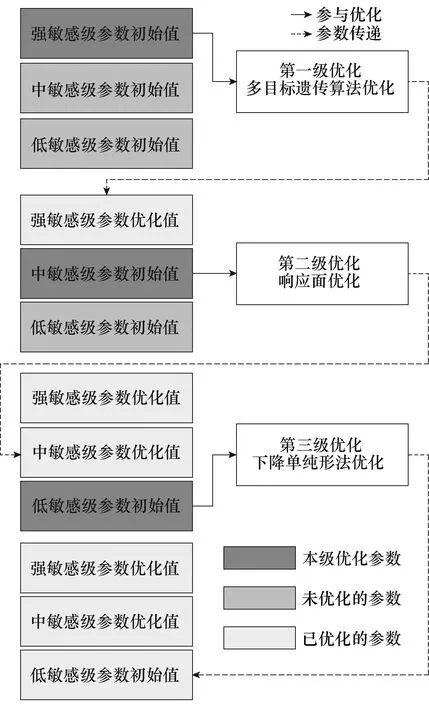
圖4 結構參數分級優化流程Fig.4 The process of structure parameter hierarchical optimization

優化中樣本的隨機性和全局性對優化結果的全局性有較大影響[25]。對此通過ALHS在優化空間中進行抽樣確定各級優化初始樣本，對于優化中的迭代環節，則通過引入自適應策略確定每次迭代的樣本（以上次迭代最優值為中心進行二次 ALHS抽樣），以此提高初始樣本和迭代的隨機性與全局性。

通過歸一化的加權函數給出對優化結果進行評價的多目標優化函數[26]，有

完成一輪分級優化后，對優化結果在所給出的優化環境下的全局性進行判斷：將優化后的結構參數作為初始值，導入優化流程進行二次搜索。如果二次搜索后的多目標優化函數數值gmin相比一輪結果降低幅度在 1%以下，則判斷一輪結果在所給出的優化環境下具有較好的全局性，并將一輪結果作為結構參數最終優化結果進行輸出。否則將二輪結果再次作為輸入進行下一輪全局搜索，直至滿足全局性要求。上述流程即為優化結果全局性判斷流程，如圖5所示。

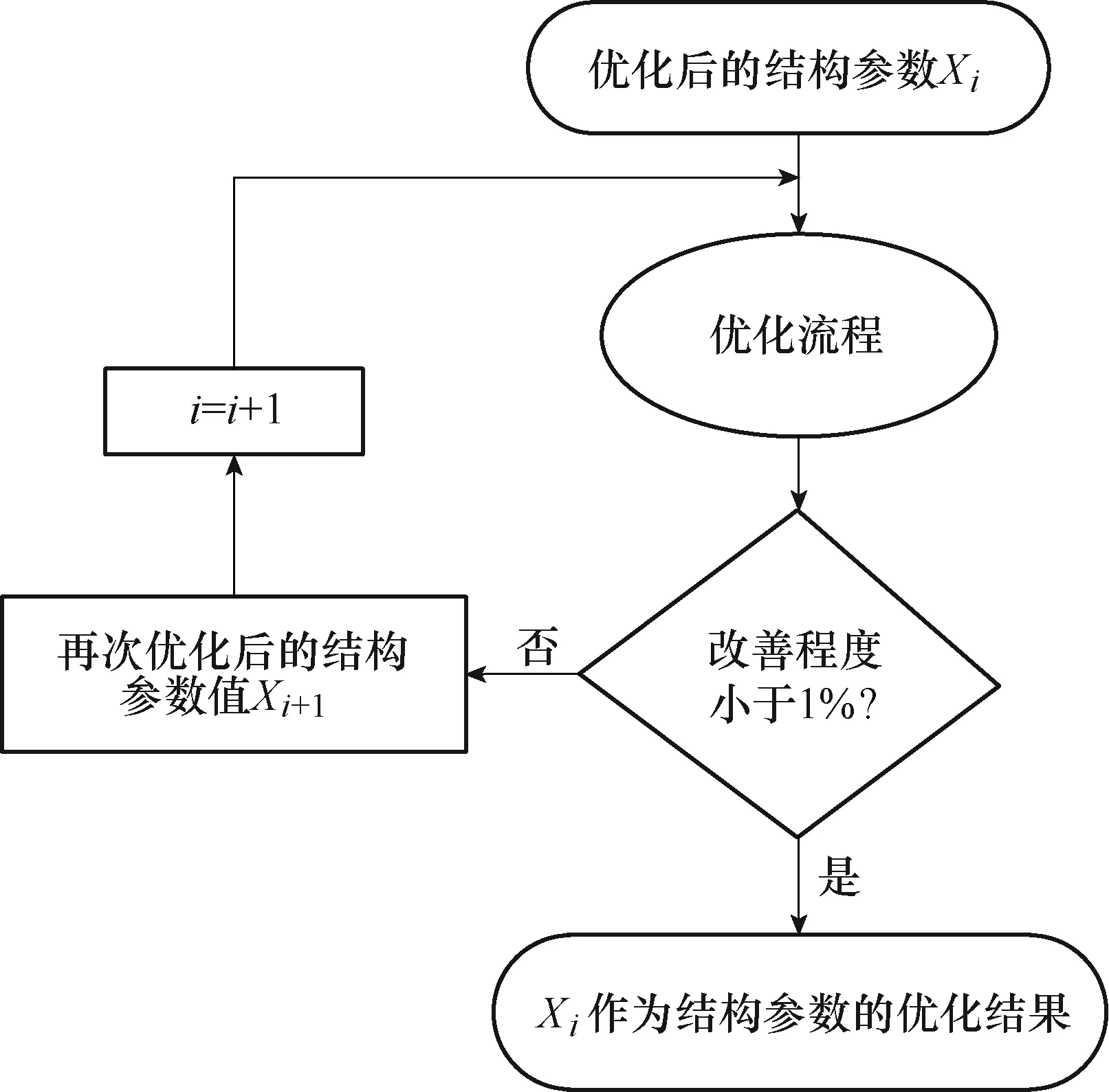
圖5 優化全局性判斷流程Fig.5 The progress of optimization globality judgment

2.3.1 強敏感級參數的一輪優化

強敏感級結構參數具有以下特點：①共4個結構參數，對3個優化目標均有影響，屬于多參數多目標優化，構造結構參數與優化目標之間的直接函數關系較困難；② 4個結構參數對優化目標影響較大，需要較高的優化深度，計算量較大；③ 3個優化目標之間存在權衡，p(t,θ)、WT的降低往往需犧牲Tavg(t)。

針對強敏感級參數的特點，采用多目標遺傳算法（Multi-Objective Genetic Algorithm, MOGA）進行全局優化。優化過程中可以基于多目標優化函數gmin(xi)快捷地對結構參數樣本進行評價；優化收斂性較好，無需過多調用求解器求解樣本；針對多目標優化以及優化目標之間的權衡，可通過Pareto前沿面的方式直觀地給出最優解[27]。

優化設置方面：設置初始樣本數為20；最低衍化代數為5代，最高衍化代數為20代；采用自適應的變異方式確定下一代的樣本，變異比例為20%。

優化計算完成后，每一代優化目標函數最小值對應的設計點構成Pareto前沿面如圖6所示。可以看出，越處于“前端”的點，徑向力密度峰值p(t,θ)越小，切向電磁轉矩均值Tavg(t)越高，同時轉矩波動比例WT越小，對應多目標優化函數數值越小。因此，最前點對應的結構參數值為本級參數優化的最優值，結構參數以及優化結果相對于初始數值的變化見表4。

圖6 優化目標Pareto前沿面Fig.6 The Pareto front surface of optimization target

表4 強敏感級優化后參數與目標數值變化Tab.4 The value change of parameter and target after optimization of strong sensitivity level

可以看出，強敏感級參數經過MOGA優化后，各項優化指標均得到一定程度的優化，其中，徑向電磁力密度峰值p(t,θ)降低28.94%，切向電磁轉矩均值Tavg(t)小幅度提高3.6%，轉矩波動比例WT大幅降低75.19%。完成優化后，4個強敏感級參數數值修正為優化后的數值，作為定值參與后續優化。

2.3.2 中敏感級參數的一輪優化

中敏感級結構參數具有以下特點：①共有3個結構參數，影響的優化目標共兩個，其中，Bs0與Hs0主要與徑向電磁力密度峰值p(t,θ)有關，與輸出轉矩平均值Tavg(t)有關的僅有Bs1，且敏感性較低，因此，本級優化認為是對p(t,θ)的單目標優化；②由于結構參數與優化目標相對較少，通過數值優化法構造擬合函數無需采集過多的樣本；③結構參數對優化目標仍存在一定程度影響，直接優化收斂慢。

基于中敏感級參數的上述特點，采用響應面法（Response Surface Method, RSM）作為本級優化方法。由于本級優化為單目標三參數優化，通過多項式擬合構造的目標函數不會過于復雜，同時可通過求解極值便捷地給出本級優化最優解。

p(t,θ)與結構參數之間關系的二次擬合多項式[28]表示為

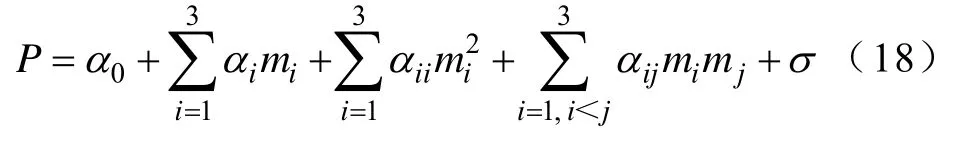
其中

式中，α0～αij為多項式系數；σ0為誤差；mi為本級的優化參數。

完成計算后，得出的響應面如圖7所示。

圖7 響應面法計算結果Fig.7 The result of RSM

求解響應面方程，得到P極小值以及對應的結構參數值，中敏感級參數優化后參數與目標數值變化見表5。

表5 中敏感級參數優化后參數與目標數值變化Tab.5 Value change of parameters and targets after the optimization of medium sensitivity level

對于受中敏感級參數影響的優化目標，可以看出，經過RSM優化后，徑向電磁力密度峰值p(t,)θ降低6%，得到進一步優化；受Bs1數值變化的影響，切向電磁轉矩均值Tavg(t)出現1.5%的小幅降低。

此外，Bs0、Bs1、Hs0數值的變化并未引起轉矩波動比例WT的數值變化。由此可以看出，中敏感級3個結構參數主要對p(t,)θ、WT產生影響，與表3給出的結論（3）一致。

完成第二級的優化后，3個中敏感級參數數值修正為優化后的數值，與修正后的強敏感級參數一起作為定值參與第三級弱敏感級參數的優化。

2.3.3 弱敏感級參數的一輪優化

弱敏感級結構參數具有以下特點：①包含Bs2和Hs2兩個結構參數，主要對切向電磁轉矩均值Tavg(t)產生影響；②影響水平較低，結構參數的數值變化不會導致Tavg(t)的劇烈變化，采用直接尋優法進行優化可較快得到收斂結果，不會導致計算效率過低。

基于上述特點，采用下降單純形法（Downhill Simplex Method, DSM）對弱敏感級參數進行優化。其通過采集一定樣本，在空間中構造一個初始單純形。通過對該單純形進行幾何變換（移動、縮放、旋轉等）使單純形逼近優化目標的極值。其中，每一次迭代單純形的變化方式通過自適應原則進行確定。當單純形縮小到最小值，或后續變化若持續收斂于所逼近的極值，則判斷 DSM 收斂，本級優化結果實現最優[29]。

基于上述過程，對Bs2和Hs2的單純形變換進行收斂計算，由于 DSM 要求切向電磁轉矩均值以極小值為優化目標，因此，對Tavg(t)取相反數。優化收斂過程如圖8所示。

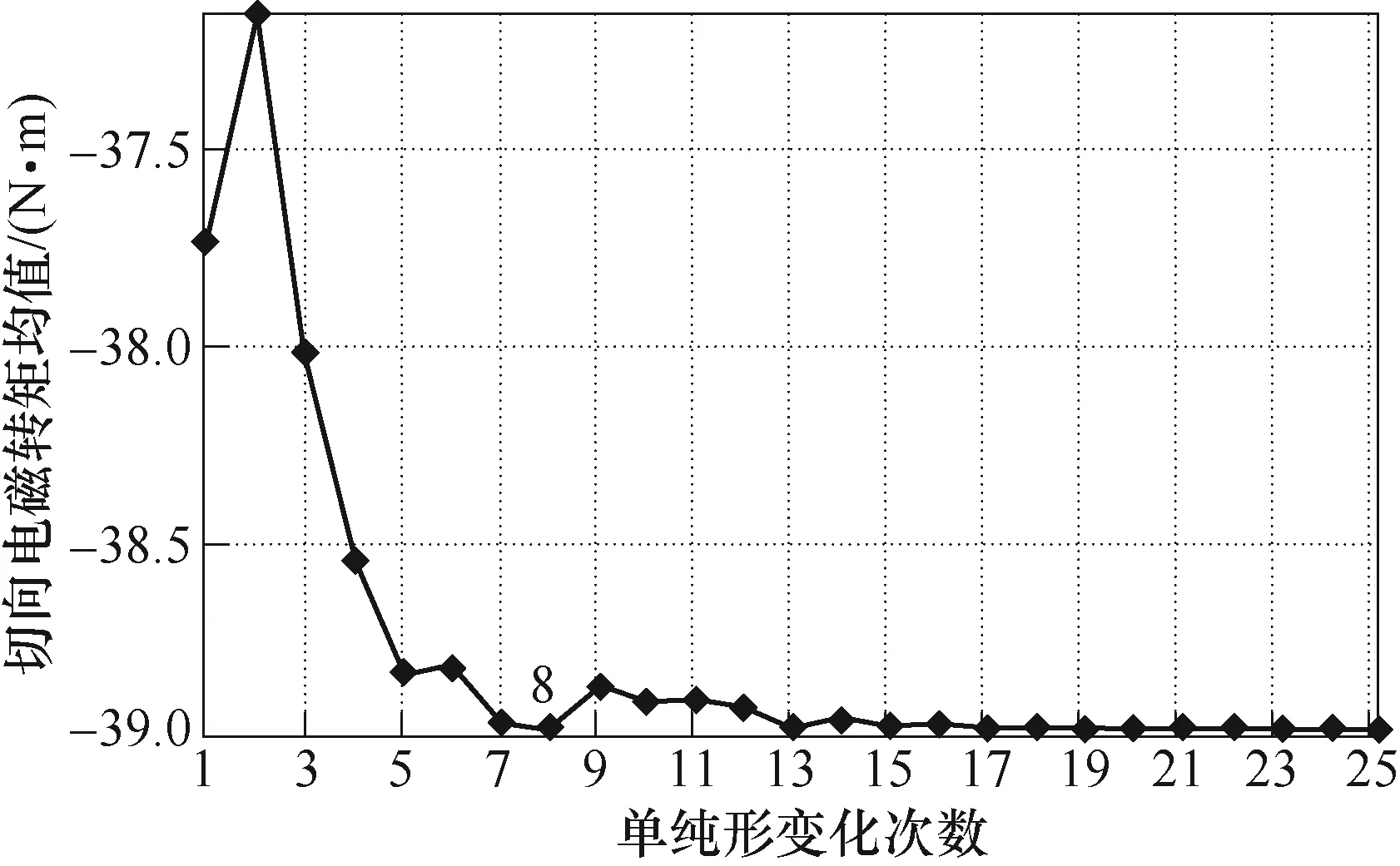
圖8 弱敏感級參數優化收斂過程Fig.8 The convergence process of optimization of weak sensitive parameters

根據優化收斂過程可以看出，經過25次單純形幾何變換，Tavg(t)的相反數就收斂于極小值。第一次趨于極小值的變換為第8次單純形變換，對應本級優化最優解，其數值見表6。

表6 弱敏感級優化后參數與目標數值變化Tab.6 Value change of parameter and target after the optimization of weak sensitivity level

從而可以看出，完成第三級弱敏感級參數優化后，切向電磁轉矩均值Tavg(t)相較于第二級優化后的數值提高了4%，同時徑向電磁力密度峰值p(t,θ)、轉矩波動比例WT未受到弱敏感級參數變化的影響，與表3給出的結論（4）一致。

2.3.4 分級優化結果的全局性判斷結果

將表4、表5優化后的結果進行匯總，作為一輪優化結果并再次導入分級優化流程，在此基礎上進行二輪全局搜索，二輪全局搜索結果與一輪結果的對比見表7。

根據表7結果，二輪搜索后，多目標優化函數gmin(xi)降低了0.613%，改善程度小于1%，根據優化結果全局性判斷流程，最終輸出的結果為一輪優化結果。

表7 分級優化兩輪優化結果比較Tab.7 The results comparison between two rounds of hierarchical optimization

由此說明，9個結構參數經分級優化得到的結果在給定的優化初值、優化范圍組成的優化空間中具有較好的全局性。

2.4 分級優化與單級優化的對比

由于單級優化為9參數3目標的全局優化，適用于單目標優化的直接搜索法 DSM 無法使用；對于數值優化法RSM，為避免出現局部優化需采集大量的樣本，同時在構造擬合模型時計算代價極高，因此，也不適于單級優化；采用全局搜索法MOGA進行單級優化則無需計算任何擬合模型或函數梯度，但為了避免局部優化，相比分級優化中的強敏感級優化需要采集更多的樣本。基于上述分析，采用MOGA對結構參數進行單級優化。

單級優化采用與強敏感級優化相同的多目標評價函數，計算出的Pareto前沿面如圖9所示。為保證單級優化的全局性，對單級優化應用優化結果全局性判斷流程，相應的結果對比見表8。

圖9 單級優化Pareto前沿Fig.9 The Pareto front of targets from single level optimization

表8 單級優化兩輪優化結果比較Tab.8 The results comparison between two rounds of single level optimization

二輪搜索后，多目標優化目標函數數值gmin降低了0.04%，小于1%，由此說明了9個結構參數經單級MOGA優化得到的結果在給定的優化初值、優化范圍組成的優化空間中具有較好的全局性。

因此，單級優化也以一輪結果作為結構參數優化的輸出結果。

以下將根據表7和表8，對單級優化與分級優化在優化效果、優化方法適應性以及優化計算量方面的水平進行對比。

在優化效果方面，對于降低徑向電磁力密度峰值的優化目標，相較于初始結果，單級優化實現了27.63%的峰值降低，同時分級優化實現了32.89%的峰值降低；在轉矩波動比例方面，單級優化降低了68.50%，而分級優化則實現了75.19%的轉矩波動降低；在切向電磁轉矩均值方面，單級優化相較初始結果提升了 5.38%，分級優化相較于初始結果提升了6.14%。

優化方法適應方面，對優化結果做進一步的觀察，可以發現，單級優化的優化效果與分級優化強敏感級參數優化的效果相當，說明MOGA對于強敏感級參數可實現較高深度的優化，但對于中弱敏感級參數的優化深度較低。因此，當優化參數中強敏感級參數數量所占比例更高時，MOGA可以獲得更高效的利用，即更為適應所優化的參數。

通過比較分級優化與單級優化的求解器調用次數表征分級優化與單級優化的計算量。分級優化的3個敏感級優化分別調用求解器200次、14次與25次，全局性判斷中調用次數分別為190次、14次與25次，分級優化合計468次；而單級優化一輪優化和二輪全局性判斷流程調用次數分別為 300次和240次，共 540次。因此，在對同樣數量且敏感性不同的參數進行優化時，分級優化計算量低于單級優化。

綜上所述，當優化過程屬于多參數多目標優化，且各參數所影響的優化目標數量與影響程度不一時，分級優化在優化效果、優化方法適用性與優化效率上，相對采用MOGA的單級優化能實現一定程度的改善。

2.5 優化結果的有限元驗證

由于在分級優化中電磁力與轉矩模型的數值來自優化目標函數的求解，因此，需要將優化后的結構參數導入有限元模型驗證實際結果是否與優化過程的計算結果一致，以驗證優化的可靠性[30]。

對徑向電磁力在氣隙中心圓周分布與切向電磁轉矩時間分布曲線進行計算，分別如圖10和圖11所示。p(t,)θ、Tavg(t)與WT的分級優化、有限元驗證以及優化前的結果的對比見表9。

表9 分級優化后優化目標有限元計算結果Tab.9 The finite results of the target value after the hierarchical optimization

圖10 徑向電磁力密度在氣隙圓周上的分布Fig.10 Distribution of radial electromagnetic force density on the air gap circumference

圖11 輸出電磁轉矩的時間分布Fig.11 The time distribution of the output electromagnetic torque

與分級優化給出的目標數值相比，p(t,)θ有限元計算結果與分級優化給出結果一致，Tavg(t)與WT的結果則存在誤差范圍內的微小差距，基于該結論認為優化結果具有可靠性。

3 結構參數優化的電磁噪聲抑制效果驗證

由于上述分級優化未直接對電磁噪聲水平進行抑制優化，因此本節將通過結構聲學仿真計算結構參數分級優化后的電機電磁噪聲水平，并與初始參數下的電磁噪聲水平進行對比以驗證抑制與改善效果。

根據優化后的結構參數，建立定子的三維模型。由于在電磁計算中采用 1/4模型以提高計算效率，因此所建立的定子三維模型由4段1/4模型組成。同時按照網格質量大于0.7的要求劃分六面體網格。定子三維模型與網格模型如圖12所示。

圖12 定子三維模型與網格模型Fig.12 The 3D model and grid model of stator

定子材料按DW360?50的機械參數進行定義，其中，等效彈性模量由于受硅鋼片疊壓過程中產生的間隙的影響，按照實心材料的75%進行定義。

本文采用等輻射聲功率級（Equivalent Radiated Power Level, ERPL）對電磁噪聲水平進行表征。相較于聲壓級（Sound Pressure Level, SPL），ERPL更能表現出噪聲自身能量水平，且不易受傳播過程的影響，ERPL的計算方式[19]為

式中，L0為參考聲功率級，數值為10?12W；L為聲功率，有

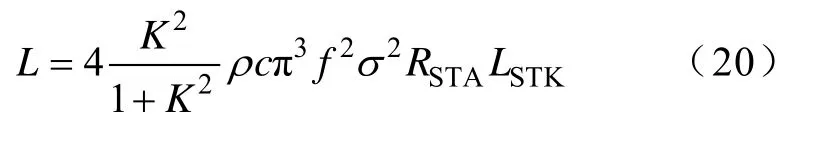
其中

式中，ρ為鐵心密度；c為聲速；f為激勵頻率；σ為定子在電磁力作用下產生的形變；RSTA為定子外徑；LSTK為定子疊壓長度。考慮定子電磁噪聲水平高于轉子且電磁激勵主要集中分布于定子齒面，選擇在定子齒面導入電磁有限元計算的氣隙電磁激勵，包括徑向電磁力與切向轉矩，導入的氣隙電磁激勵與其作用面如圖13所示。圖中，圓環即為所導入的電磁激勵。

圖13 導入的氣隙電磁激勵與其作用面Fig.13 The input air gap electromagnetic excitation and its applied surface

采用模態疊加法求解 ERPL，其中，激勵頻率區間為0～10kHz，并按照總步數為50步進行頻率分解，求解各頻率下的ERPL。

為了對抑制效果進行驗證，按照優化前的結構參數建立定子模型，導入優化前的氣隙電磁激勵并同樣采用模態疊加法對優化前的ERPL進行求解。優化前后結果對比如圖14所示，其中，ERPL為負值的點由于不具備工程意義，對其取零值處理。

優化前后ERPL峰值、峰值對應激勵頻率，以及定子整體的ERPL平均值見表10。

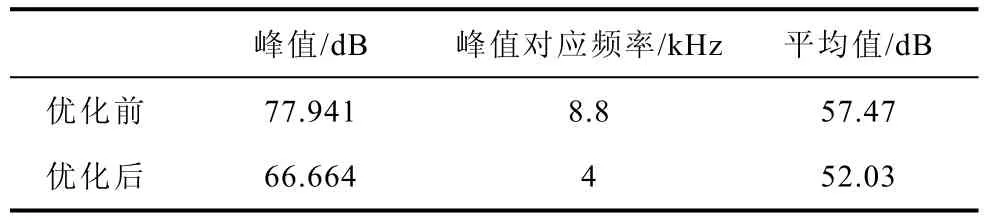
表10 優化前后電磁噪聲水平對比Tab.10 The comparison of origin and optimized electromagnetic noise level

可以看出，優化后ERPL峰值降低了14.47%，平均值降低了 9.47%，因此，優化后的電磁噪聲水平在強度上得到了有效抑制；同時ERPL峰值對應的電磁激勵頻率有所降低，且從圖14可以看出，優化后 6～10kHz的 ERPL幅值相較于優化前降低明顯，因此，電磁噪聲高頻尖銳度得到有效改善，聲品質水平得以提高。綜上所述，對結構參數進行分級優化后，電機電磁噪聲強度得到有效抑制，同時電磁噪聲的聲品質也得到改善。

圖14 優化前后ERPL對比Fig.14 The comparison of origin and optimized ERPL

4 結論

1）為保證不以降低電機性能為代價抑制電磁噪聲，以徑向電磁力密度峰值最小、切向電磁轉矩均值最大以及輸出轉矩波動比例最小為優化目標。

2）通過基于多項式擬合的關鍵系數計算了結構參數對優化目標的敏感程度，從而對結構參數進行篩選與敏感性分級。

3）綜合MOGA、RSM以及DSM，根據結構參數的敏感性等級對其進行分級優化，并對全局性進行驗證。結構參數優化后徑向電磁密度峰值降低32.89%，輸出轉矩平均值提高 6.14%，轉矩波動比例降低75.19%。

4）通過比較單級優化與分級優化的優化效果、優化方法適用性以及優化效率，說明在本文給出的優化環境下，分級優化在上述三個方面相較單級優化均有所改善。

5）通過結構聲學仿真驗證了結構參數優化后的電磁噪聲抑制效果和聲品質改善效果。結果顯示，ERPL峰值降低了14.47%，平均值降低了9.47%；同時高頻尖銳度相較于優化前明顯降低。因此，認為電磁噪聲強度得到了有效抑制的同時噪聲聲品質也得到了改善。