響應曲面法優化Fenton 氧化處理印染廢水

秦 宇，吳慧芳，陳 文，徐 杰，侍路夢

（南京工業大學城市建設學院，江蘇南京 211816）

我國是傳統的紡織大國。據統計，我國每年的印染廢水排放量為65 億t 左右，占工業廢水排放量的35%［1］。印染廢水具有污染物濃度高、有毒有害、色度高以及可生化性差等特點［2-4］。由于印染廢水的可生化性較差，所以傳統的生化法處理效果不佳，而且現在排放標準更加嚴格，傳統工藝達不到排放標準要求［5］，需要對傳統工藝進行改良。高級氧化法是在氧化劑作用下實現對污染物的降解，污染物去除效果較好且穩定，其中Fenton 氧化法越來越受到關注［6-8］。

Fenton 氧化法的機理：H2O2在Fe2+的催化作用下產生具有強氧化性的羥基自由基（HO·）氧化污染物，Fe2+被氧化成Fe3+，具有混凝沉淀作用，能夠去除污染物［7-8］。Fenton 氧化技術具有設備簡單、操作簡便、應用范圍廣、氧化能力強和處理效果好等優點［9-10］，然而極易形成鐵泥。因此，Fenton 氧化法的應用關鍵是提高Fenton 處理效率，減少藥品用量，從而減少鐵泥生成量。影響Fenton 氧化處理效率的主要因素有Fe2+用量、H2O2用量、溶液pH、反應時間及污染物初始質量濃度等。Kang 等［11］分別研究了pH、Fe2+用量和H2O2用量對Fenton 法處理垃圾滲濾液的影響，得出pH 的影響最大。Gulkaya 等［12］通過單因素實驗研究了4 個主要因素對Fenton 氧化法處理地毯紡織廢水的影響，發現H2O2與Fe2+比值的影響最顯著。單因素實驗只能評價各因素單獨對處理效果的影響，而多因素優化實驗研究各因素間的交互作用，對Fenton 氧化法處理印染廢水具有重要意義。本實驗采用Fenton氧化法處理模擬染料廢水［13］，在單因素實驗的基礎上，研究5 個主要因素間的交互作用對染料去除率的影響，采用響應曲面法對處理效果的主要影響因素進行優化實驗［14-18］，以建立回歸方程模型預測最佳處理參數，為工程實踐提供理論依據。

1 實驗

1.1 材料

染料：酸性橙Ⅱ（分子式為C16H11N2NaO4S，最大吸收波長為395 nm）；試劑：30%過氧化氫（H2O2）、氫氧化鈉（NaOH）（分析純，國藥集團化學試劑有限公司），七水合硫酸亞鐵（FeSO4·7H2O，分析純，南京化學試劑有限公司），硫酸（H2SO4，分析純，上海凌峰化學試劑有限公司）。

1.2 廢水處理

取一定體積的模擬染料廢水于燒杯中，加入一定量FeSO4·7H2O 溶液，調節pH，加入一定量30%H2O2，攪拌并計時。反應用NaOH 終止，離心后取上層清液，采用紫外分光光度計在酸性橙Ⅱ的最大吸收波長下測定吸光度，根據質量濃度與吸光度標準曲線計算染料去除率R=(1-ρ′/ρ)×100%，其中，ρ、ρ′分別為處理前后染料的質量濃度。

1.3 響應曲面實驗方案

對模擬酸性橙Ⅱ染料廢水進行單因素實驗，考察FeSO4·7H2O 用量（A，g/L）、H2O2用量（B，mL/L）、溶液pH（C）、反應時間（D，min）及染料初始質量濃度（E，g/L）對染料去除率的影響。結果表明：當A=0.025、B=0.25、C=3.5、D=130、E=0.25 時效果較好，以此為中心點，應用Design Expert 8.0 軟件進行Box-Behnken中心組合設計［19］。在單因素實驗的基礎上選取5 個因素的高（+1）、中（0）、低（-1）3 個水平，共計46 個實驗點進行實驗。

2 結果與討論

2.1 去除率回歸模型分析及優化

中心組合設計方案及結果見表1。

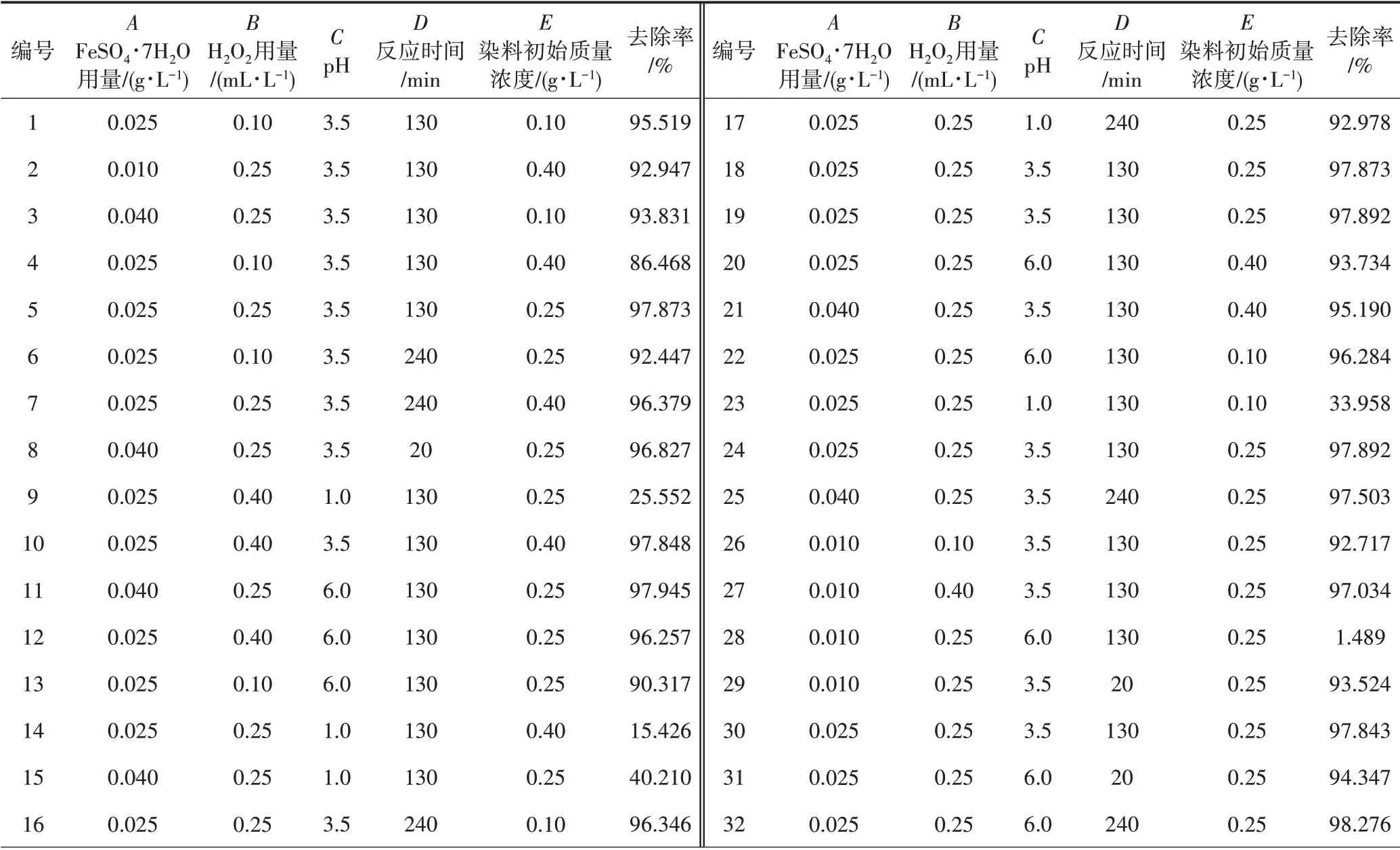
表1 中心組合設計方案及結果

續表1

利用統計軟件Design Expert 8.0 對表1 的實驗數據進行回歸分析，建立二次回歸模型并優化。優化前響應曲面二次回歸模型方差分析見表2。

表2 優化前回歸模型的方差分析

概率P值（prob＞F）越小因素影響越顯著［20］。由表2 可知，模型的P值遠小于0.01，說明模型高度顯著。Fenton 氧化法的5 個因素中，僅有C及其二次方（C2）影響顯著，其余各因素及其交互作用影響顯著性都低。二次回歸模型擬合系數R2=0.782 9，調節擬合系數Radj2=0.609 2，模型預測值擬合系數Rpred2=0.131 5，Adeq Precision=7.546。根據響應曲面法原理，Rpred2與Radj2應非常接近，合理偏差應小于20%；而此回歸模型中兩者相差甚大，說明模型需要進行降階或剔除離群點等優化。

經觀察分析，對此模型進行剔除離群點優化。圖1a 為優化前實驗值與模型預測值對比圖，除圖中兩個空心點（即表1 中編號為7 和15 的兩個實驗點）離斜線較遠外，其余點都表明實驗值與模型預測值相同，所以將這兩個離群點剔除，對模型進行優化，重新進行回歸分析，結果見圖1b。

圖1 實驗值與模型預測值對比圖

由表3 可看出，在Fenton 氧化法中，B及其二次方（B2）、C及其二次方（C2）、E均對去除率影響顯著。結合P值和F值［18］，各參數單獨對去除率的影響顯著性從大到小為溶液pH、H2O2用量、染料初始質量濃度、FeSO4·7H2O 用量、反應時間。FeSO4·7H2O 用量和溶液pH、pH 和反應時間、pH 和染料初始質量濃度的交互作用顯著，其中AC的F值最大，P值最小，此兩因素的交互作用相比其他因素的交互作用對酸性橙Ⅱ去除率的影響更顯著。

表3 優化后回歸模型的方差分析

2.2 去除率響應曲面圖分析［19，21］

為考察各因素交互作用對染料去除率的影響，固定其他因素不變，可獲得任意兩個因素交互作用對去除率影響的響應曲面圖。根據表3 選取交互作用相對顯著的影響因素組合進行分析。三維曲面的最凸點對應的響應值最大；等高線的形狀反映交互作用的強弱，等高線越密交互作用越顯著，橢圓表示交互作用顯著，圓形表示交互作用不顯著［17］。

由圖2a 可知，在FeSO4·7H2O 用量固定時，去除率隨著pH 的變化先增大后減小；不同FeSO4·7H2O 用量對應不同的最佳pH。當3.5＜pH＜6.0且固定時，去除率隨著FeSO4·7H2O 用量的增加而降低；而當1.0＜pH＜3.5 且固定時，去除率隨著FeSO4·7H2O 用量的增加而升高，因此響應曲面有扭轉。等高線圖2b 呈明顯的扁平橢圓，橢圓端點已超出圖外，等高線較為緊密。說明FeSO4·7H2O 用量和pH 交互作用顯著。

圖2 FeSO4·7H2O 用量和pH 交互作用的響應曲面(a)及等高線(b)圖

由圖3a 可以看出，當反應時間固定時，去除率隨著pH 的增加先增大后減小；不同反應時間對應不同的最佳pH，但最佳pH 均為3.5～5.0。等高線圖3b 形狀為明顯的橢圓，等高線緊密。這說明兩者的交互作用顯著性好。

圖3 pH 和反應時間交互作用的響應曲面(a)及等高線(b)圖

由圖4a 可知，當染料初始質量濃度不變時，隨著pH 的增加，去除率先升高后降低；pH 固定時，去除率隨染料初始質量濃度的增大而降低。等高線圖4b 緊密，形狀為橢圓。說明pH 和染料初始質量濃度交互作用顯著。

圖4 pH 和染料初質量始濃度交互作用的響應曲面(a)及等高線(b)圖

2.3 二次模型方程擬合及最佳條件

利用統計軟件Design Expert 8.0對優化后的二次模型進行方程擬合，得到5個因素與染料去除率的回歸方程為：R=-30.704+918.741A+38.320B+54.520C-4.712×10-2D-52.181E+259.444AB-245.710AC-0.482AD+589.000AE+1.752BC+6.606×10-3BD+121.089BE+1.635×10-2CD+10.655CE+1.797×10-2DE-2 191.397A2-128.412B2-5.639C2-1.980×10-5D2-91.545E2。

在二次模型的基礎上，利用軟件響應曲面進行優化，要求響應值去除率最大，得出對應的優化反應條件。在各因素約束條件（0.010≤A≤0.040，0.10≤B≤0.40，1.0≤C≤6.0，20≤D≤240，0.10≤E≤0.40）下，考慮去除率的實際意義（0%≤R≤100%），軟件設置響應值去除率最大，得到優化反應條件為A=0.022、B=0.12、C=4.4、D=21、E=0.23。考慮實際操作，實驗時修正優化條件為A=0.020、B=0.10、C=4.5、D=20、E=0.25，去除率達96.85%，模型回歸方程預測值為99.31%，兩者偏差小于3%。

3 結論

（1）采用響應曲面法優化Fenton 氧化法處理模擬染料廢水，以染料去除率為響應值，得到二次回歸模型方程。回歸模型方程的顯著性較高，R2=0.991 1，Radj2=0.983 3，Rpred2=0.958 7，Adeq Precision=37.032，回歸效果好，預測精度高，可進行預測分析。

（2）Fenton 氧化法處理模擬染料廢水的5 因素之間有一定的交互作用，各因素對染料去除率的影響顯著性由高至低排序為溶液pH、H2O2用量、染料初始質量濃度、FeSO4·7H2O 用量、反應時間。

（3）優化處理條件：染料初始質量濃度0.25 g/L，FeSO4·7H2O 用量0.020 g/L，H2O2用量0.10 mL/L，pH 4.5，反應時間20 min。此時去除率達96.85%，實驗驗證值與預測值99.31%之間的偏差小于3%。